> Дирижабли, страница 1 > Исследование равновесия корабля в вертикальной плоскости

Исследование равновесия корабля в вертикальной плоскости

Мы не можем провести исследование вопроса без ограничения его определенными условиями в отношении корпуса корабля, в связи с чем и допустим ряд гипотез.

Предположим, что:

1. Корабль не подвергается деформации, то есть характеристические кривые его соответствуют определенному положению руля (руль на нуле)¹
2. Центр объёма газовой массы находится в неизменном положении (α—неизменяемо).
3. Плотность воздуха постоянна, и не происходит изменений в температурах воздуха и газа после того, как произошло нарушение начального равновесия.
4. Положение начального равновесия установлено в состоянии покоя при нулевой сплавной силе; ось аэростата горизонтальна.

Чтобы объяснить те случаи поведения кораблей, которые обнаружились в практике современного воздухоплавания, как было отмечено в отношении случаев, приведенных в начале настоящего очерка, мы рассмотрим реакции, вызванные:

1. Воздействием силы тяги винтов;
2. Воздействием вертикальных сил (изменения нагрузки)-положительных или отрицательных;
3. Одновременным воздействием этих двух категорий сил.

Реакции, вызываемые нарушением равновесия силами тяги, то есть силами определенного направления относительно направления линии нулевого поддержания

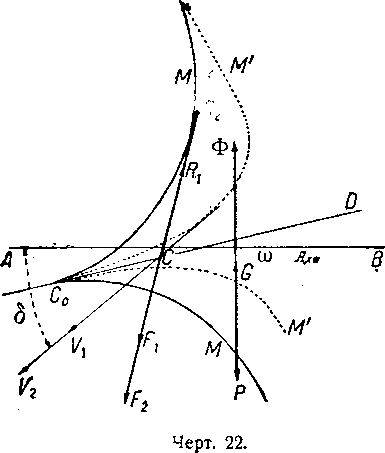
Рассмотрим корабль (чертёж 22) при нулевой сплавной силе, уравновешенный при диференте, равном нулю. Вследствие наличия гондол корабль является несимметричным, и направление линии нулевого динамического поддержания наклонено относительно того направления оси, когда дифе-рент равен нулю.

Мы немедленно обнаруживаем, что направление тяги касательной к метацентрической кривой дает положение равновесия при диференте, равном нулю. В этом частном случае направление сопротивления воздуха прямо противоположно облической силе тяги, и пара статической устойчивости действия не оказывает.

Мы имеем CF₁=CR₁ для направления скорости CV₁, величина которой равна CV₁. Повысим величину силы тяги с CF₁ до CF₁, диферент при равновесии корабля остается равным нулю и мы имеем CF₂=CR₂ для того же направления скорости, которое лишь изменяется с величины CV₁до большей величины CV2. Угол атаки остается неизменным.

(¹ Имеется в виду вся линия очертания корабля, включая оперение. Примечание редакции.)

Направление тяги не является касательной к метацентрической кривой. Величина пары сил от работы моторов.

Обычно направление силы тяги не является касательной к метацентрической кривой. Из этого следует, что величина диферента при равновесии будет функцией величины пары сил, каковую и надлежит установить

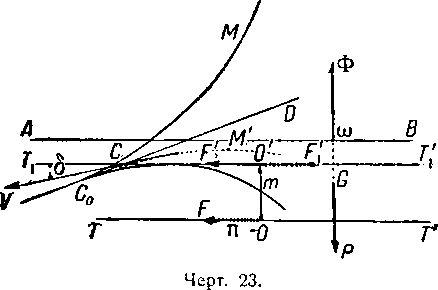
Возьмем аэростат в его исходном положении и пусть ТТ′—направление тяги, величина которой OF=π. Проведем касательную Т′Т₁′ к метацентрической кривой, параллельную направлению ТТ′ (чертёж 23).

Сила OF может быть заменена равной силой O′F′, приложенной по направлению T₁T₁′, и парой FOO′F₁′.

Поскольку сила O′F′ сохраняет диферент равным нулю, ибо она является касательной к метацентрической кривой, диферент, вызванный силой OF, будет при равновесии определен величиной пары π×m, которая является парой от действия моторов, где m=OO′.

Когда равновесие будет достигнуто, мы будем иметь:

Р·а·sin θ=π×m или

sin θ=	π×m
	Р·α

— отношение, дающее величину диферента.

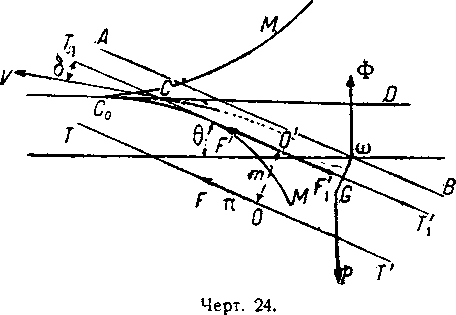
Величина угла атаки δ остается неизменной (чертёж 24).

Возьмем вновь исходное положение равновесия и увеличим силу тяги с π₁ до большей величины π₂. Пара изменится с величины π₁×m до большей величины π₂×m; следовательно, величина диферента при равновесии увеличится, и мы будем иметь диферент θ₂, при котором

sin θ2=	π2×m
	Р·α

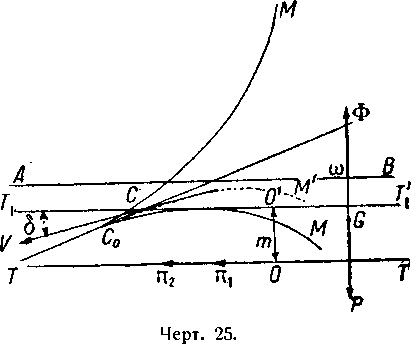
Здесь θ₂ больше, чем θ₁ (чертёж 25). Что же касается величины угла атаки, то она остается неизменной и равной δ.

Итак:

1) Силы определенного направления в корабле характеризуются в своем действии существенным фактом: величина угла атаки остается неизменной, каковы бы ни были величина рассматриваемой силы и величина диферента при равновесии.

2) Величина пары от моторов дается выражением π×m, причем m является расстоянием между направлением рассматриваемой силы и прямой, параллельной этой силе, проведенной касательно к метацентрической кривой.

Следовательно, представляется невозможным определить величину этой пары, если положение касательной к метацентрической кривой неизвестно и если ее положение не определяется опытами в полете.

3) Всякое изменение силы тяги влечет за собой соответственное изменение величины диферента при равновесии, которое дается уравнением

sin θ=	π×m
	Р·α

4) В частном случае, когда направление тяги является касательной к метацентрической кривой, диферент при равновесии неизменно устанавливается на нуль независимо от величины рассматриваемой силы.

Реакции корпуса дирижабля — тяжелого, поднимающегося, имеющего руль „полностью на спуск”, при изменении скорости полета.

Пусть АВ будет направлением линии нулевого поддержания поднимающегося дирижабля, идущего с углом пути α, несмотря на руль, поставленный „полностью на спуск“, вследствие утяжеления р. Угол атаки равен δ (чертёж 26). На первый взгляд представляется, что увеличение скорости корабля, поскольку оно дает большую отдачу руля, обеспечивает возможность удерживать постоянную высоту.

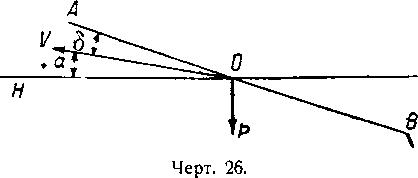
Действительно, при маневрировании кораблями в горизонтальной плоскости увеличение скорости полета ускоряет эволюцию. Однако при маневрировании в вертикальной плоскости вопрос обстоит совершенно иначе, так как здесь мы имеем дело не с эволюцией корабля, a c переходом его из состояния равновесия при подъеме к другому состоянию равновесия при горизонтальном полете.

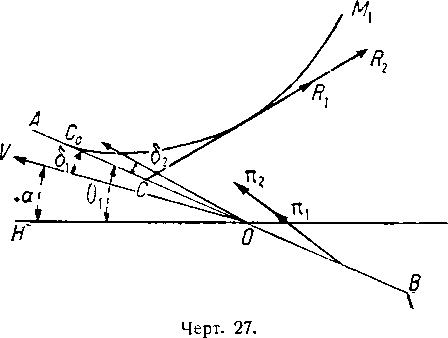
Мы увидим, что в этих условиях, как это показывает и опыт, результаты воздействия тяги заметно тличаются от тех, которые обычно предполагались. Пусть АВ будет линией нулевого поддержания корабля. Этот корабль с отклоненным рулем пусть будет представлен метацентрической кривой М₁; пусть CR₁ будет сопротивлением воздуха при равновесии для случая тяги π₁ (чертёж 27). Взятая изолированно эта тяга дает, например, угол атаки δ₂; увеличивая тягу, мы оставляем этот угол δ₂ неизменным, а угол диферента будет изменяться лишь под действием величины динамической опрокидывающей пары, вызываемой сопротивлением воздуха, которое возрастает от величины CR₁ до величины CR₂.

При нормальном увеличении скорости положение точки С существенно не изменяется, а угол атаки, созданный весом р, стремится уменьшиться вследствие увеличения скорости; диферент увеличивается, и аэростат поднимается более быстро.

При уменьшении скорости полета угол атаки, вызываемый тягой, остается постоянным, а угол атаки, создаваемый весом, увеличивается вследствие уменьшения скорости; опрокидывающая пара ослабляется, угол диферента быстро уменьшается в своей величине и вскоре становится равным углу атаки. Полет на постоянной высоте может быть восстановлен.

Следовательно, всякое увеличение хода ускоряет подъем, и единственно возможным маневром для удержания постоянной высоты является уменьшение скорости полета.

Реакция корабля при нарушениях равновесия положительными или отрицательными вертикальными силами

В этом случае рассматривается вопрос о реакциях, вызываемых облегчением или утяжелением дирижабля; эти силы проходят через определенную точку, имея определенное направление в пространстве. Опыт показывает, что феномены изменения веса могут вызываться различным образом, ввиду чего следует рассмотреть каждый случай в отдельности.

1. Утяжеление или облегчение могут быть соответственно вызваны хлопком клапана или сбрасыванием баласта.

2. Как указано в сообщении командира эскадрильи Причара, имеют место дневное облегчение и ночное утяжеление корабля,

3. Утяжеление или облегчение может явиться вследствие возникновения разницы в температуре воздуха и газа в какой-нибудь данный момент; это явление было установлено на „Диксмюде“. Если мы возьмем описанный в начале этого очерка опыт с „Диксмюде“, то увидим, что различие в температуре воздуха и газа, примерно, в 5° держалось в течение двух с половиной часов, а затем, при прохождении корабля через довольно густое облако, температура немедленно уравнялась.

Когда температура воздуха выше температуры газа, корабль облегчается, а когда температура воздуха ниже температуры газа, мы имеем утяжеление корабля.

4. Постепенное облегчение во время полета вследствие расхода горючего. Это облегчение компенсируется потерей газа; газ этот удаляется таким образом, что сохраняется статическое равновесие корабля.

С динамической точки зрения это облегчение представляет серьезные неудобства. Действительно, пусть в начале перелета восстанавливающая пара будет P·α; тогда для данного утяжеления р корабль будет иметь угол диферента θ₁ при данном режиме работы моторов.

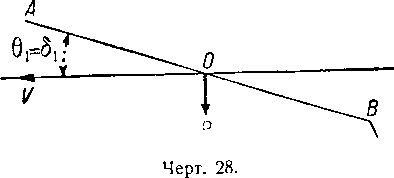
Предположим, что при этом положении для удержания постоянной высоты руль будет установлен „полностью на спуск“ (чертёж 28).

В конце перелета пара статической устойчивости будет лишь (Р—Р′) α, и хотя величина а слегка возрастает, пара статической устойчивости значительно уменьшится, так как вес горючего Р′ может достигнуть четверти тоннажа.

В этих условиях для того же самого утяжеления р в конце перелета нос корабля поднимется вверх, θ₂ > θ_1; и аэростат будет подниматься при руле, установленном „полностью на спуск“. Слёдовательно, придется уменьшить скорость полета, чтобы сохранить высоту постоянной. Вследствие этого к моменту прибытия корабля маневренность его уменьшается по сравнению с моментом отбытия.

Мы рассмотрим эти различные случаи в связи с величиной статической восстанавливающей пары, так как прибавление или вычитание сил веса оказывают воздействие на ее величину; далее мы рассмотрим реагирование корабля на действие вертикальных сил, то есть „планирующий полет“ дирижабля.

Изменения веса, вызываемые маневрированием балластом или хлопком клапана.

Пусть АВ будет осью корабля при нулевой сплавной силе и пусть корабль в состоянии покоя так уравновешен, что его ось горизонтальна.

Мы имеем Ф=Р, и аэростат находится в равновесии на уровне N (чертёж 29).

Дадим хлопок клапана центральному газовому баллону. Сила, приложенная в ω, будет Р−р; с другой стороны, вес остался неизменным.

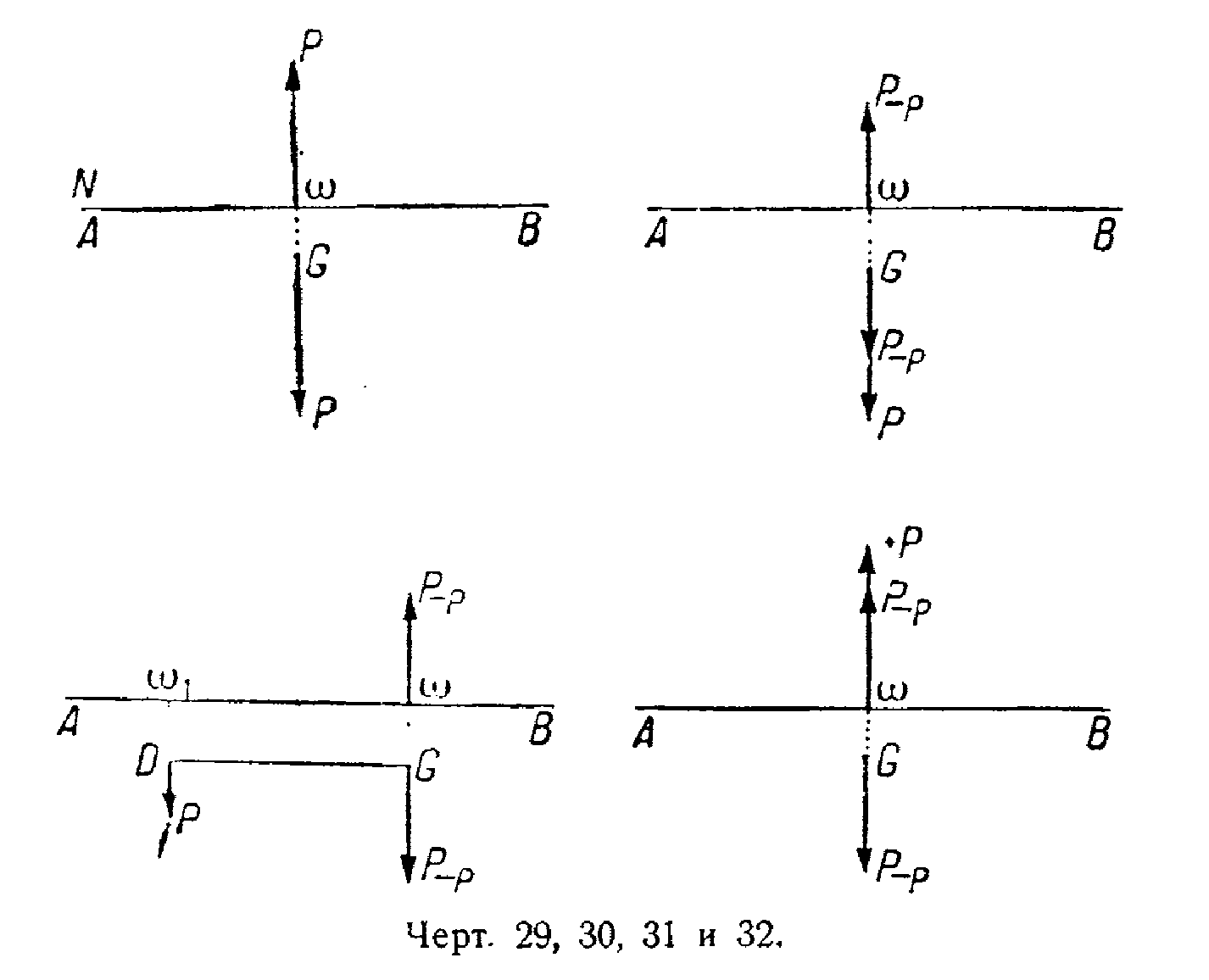
Поэтому в центре тяжести мы имеем силу (Р−р)+р. Следовательно, хлопок клапана в ω равнозначен увеличению веса на величину р, приложенную в центре тяжести аэростата, восстанавливающая пара которого равна (Р−р)·α (чертёж 30).

Если мы перенесем вес р, приложенный в G, в какую-нибудь точку D, то этот перенос веса будет соответствовать хлопку клапана, данному в точке ω₁ для аэростата, восстанавливающая пара которого равна (Р−р)·α (чертёж 31).

Рассуждая таким же образом, можно убедиться, что сбрасывание балласта в центре тяжести равнозначно приложению силы +p в центре объёма газовой массы такого аэростата, восстанавливающая пара которого равна (Р−р)·α (чертёж 32).

Следовательно, для получения точки приложения силы, утяжеляющей или облегчающей аэростат, приходится вводить поправку на величину α ¹ так как восстанавливающая пара равна (Р−р)·α.

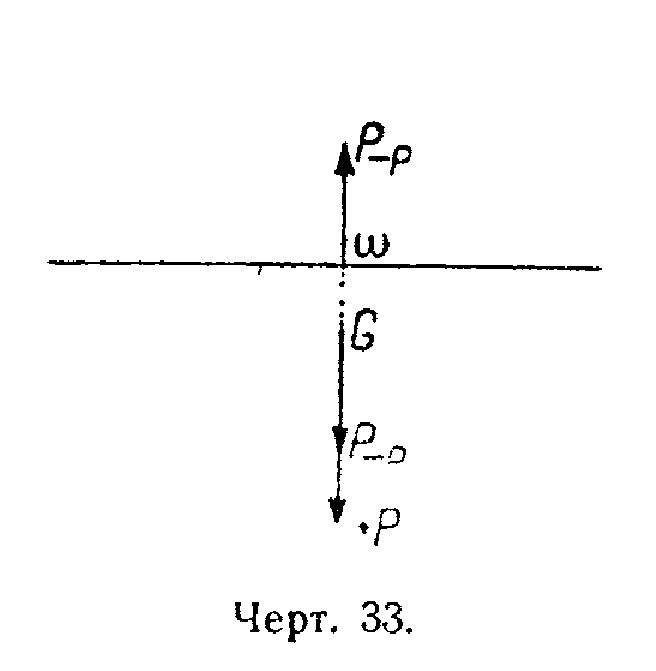
Изменения веса, вызываемые разницей температур воздуха и газа или радиацией

1. Утяжеление. В этом случае мы имеем в центре объёма газовой массы некоторую силу Р−р, а в центре тяжести—силу Р=(Р−р)+р (чертёж 33).

Следовательно, сила р приложена к центру тяжести аэростата, восстанавливающая пара которого равна (Р−р)α.

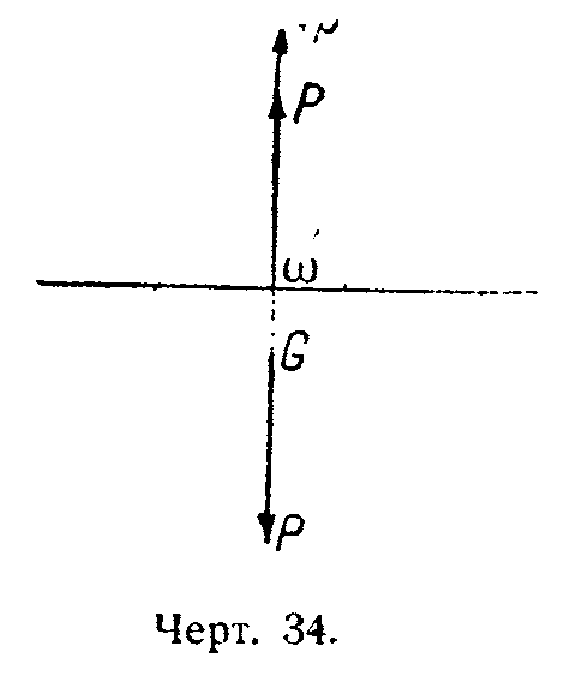
2. Облегчение. В центре объёма газовой массы мы имеем некоторую силу Р+р, а в центре тяжести—силу Р.

Сила р будет приложена в центре объёма газовой массы аэростата, восстанавливающая пара которого будет Р·α (чертёж 34).

Мы видим, что этот частный случай отличен от всех других; действительно, здесь имеется добавление некоторой вертикальной силы вверх и нет надобности изменять точку ее приложения.

3. Механическое утяжеление, вызываемое дождем, обледенением и так далее.

В этом случае восстанавливающая пара остается равной Р·α, и вес добавляется в некоторой точке, подлежащей определению в каждом отдельном случае.

¹ ω₁ D=a (смотрите чертёж 31).

Определение положения равновесия для случая хлопка клапана, приложенного в произвольной точке

Возьмем какой-нибудь дирижабль, статически уравновешенный на уровне N, причем ось аэростата горизонтальна.

Пусть р будет силой, нарушающей равновесие, полученной в результате хлопка клапана в ω₁ (чертёж 35). В соответствии с изложенным сила р должна быть приложена в такой точке О, чтобы ω₁О=а, тогда как восстанавливающая пара аэростата будет равна (Р−р)·а.

Пусть θ будет углом диферента при равновесии (чертёж 36).

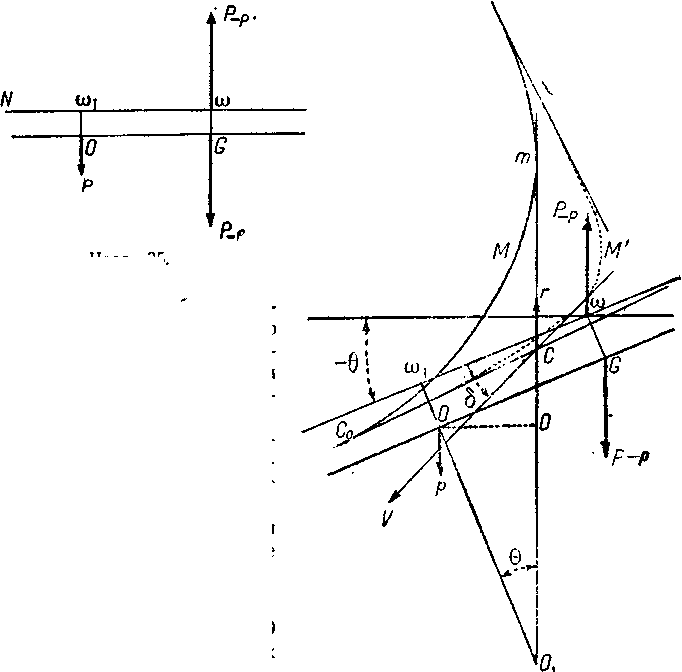
Чертёж 35. Чертёж 36.

Когда движение будет прямолинейным и равномерным, то направление силы сопротивления воздуха будет вертикальным и касательным к метацентрической кривой.

Пусть Сm будет этим направлением; тогда С будет центром девиации и CV определит собой направление движения.

Силы уравновесились, и мы имеем следующее уравнение равновесия пар: р·OD=(Р−р)·α·sin θ.

Проведем через точку О прямую, перпендикулярную к направлению¹, являющемуся началом отсчета угла наклона корабля (диферента).

Эта прямая пересечется с направлением силы сопротивления воздуха в О₁.

Следовательно:

OD=OO₁·sin θ,

что дает:

p·OO₁·sin θ=(P−p)·α·sin θ;

OO1=	P−p	·α
	p

Следовательно, перемещая точку отсчета новой величины

P−p	·α
p

¹ К оси корабля. мы получаем точку О₁ и, проводя из этой точки касательную к метацентрической кривой,мы получаем направление сопротивления воздуха, которое является вертикальным, и величину угла диферента, который определяет положение равновесия в пространстве (чертёж 36).

Возьмем дирижабль ММ′ (чертёж 37), статически уравновешенный при угле наклона корабля, равном нулю. Предположим, что Р=10 тонн; дадим в некоторой точке ω₁хлопок клапана, соответствующий силе р=2 тонны Мы видим, что этот маневр равнозначен утяжелению в O₁ на вес р такого дирижабля, восстанавливающая пара которого равна:

(Р−р)·α=(10—2)·α=8·α.

Из точки O₁ проведем перпендикуляр к направлению, определяющему диферент равный нулю, и отложим на нем величину

P−p	·α=4α
α

Мы получаем О_1^′—одну точку на направлении силы сопротивления воздуха, касательном к метацентрической кривой. О₁′С₁ является направлением этого сопротивления. Следовательно, когда установится равновесие при прямолинейном и равномерном движении, эго направление будет вертикальным; угол O₁O′₁C₁ определяет, таким образом, величину угла диферента, а направление С₁ V₁—направление движения.

Обратим внимание на положение точки приложения хлопка клапана. Проведем касательную m₂С₂ к метацентрической кривой, перпендикулярную к направлению, определяющему диферент равный нулю. Для положения ω₂, точки приложения хлопка клапана угол диферента при равновесии будет равен нулю. Это не означает, что этот угол диферента получается немедленно; в момент нарушения равновесия дирижабль произведет эволюцию, придя в движение, а затем он остановится на нулевом диференте, когда движение станет прямолинейным и равномерным (скорость постоянна).

Эта особая точка именуется точкой безразличия в диференте. Все хлопки клапаном спереди от этой точки дают положение равновесия с отрицательным наклоном, а все хлопки клапаном, произведенные сзади от этой точки, дают положение равновесия с положительным наклоном.

Направление движения — C₂V₂, угол атаки — δ₂.

Сзади от этой точки мы находим другую, заслуживающую внимания точку.

Касательная к метацентрической кривой в точке возврата С₀′ пересекается с прямой DE в О₃′ (чертёж 37). Проведем из этой точки перпендикуляр к направлению нулевого диферента.

В ω₃ мы получаем положение точки приложения хлопка клапана, который будет таким, что полученное равновесие будет характеризоваться вертикальным спуском аэростата.

Действительно, для этого положения направление сопротивления воздуха совпадает с направлением скорости, причем направление С₃О₃′ является вертикальным, а следовательно, и спуск тоже будет вертикальным.

Угол диферента равняется + θ₃, а угол атаки равен 90°+θ₃ или δ₃.

Для всех хлопков клапаном спереди от этой точки ω₃ перемещение будет происходить в направлении носа, а для всех хлопков клапаном, произведенных сзади от точки ω₃ перемещение будет в направлении кормы.

Мы дали построение равновесия и для другого хлопка клапана сзади от этой точки. Мы получаем там диферент при равновесии + θ₄и угол атаки δ₄, причем дирижабль перемещается в заднем направлении.

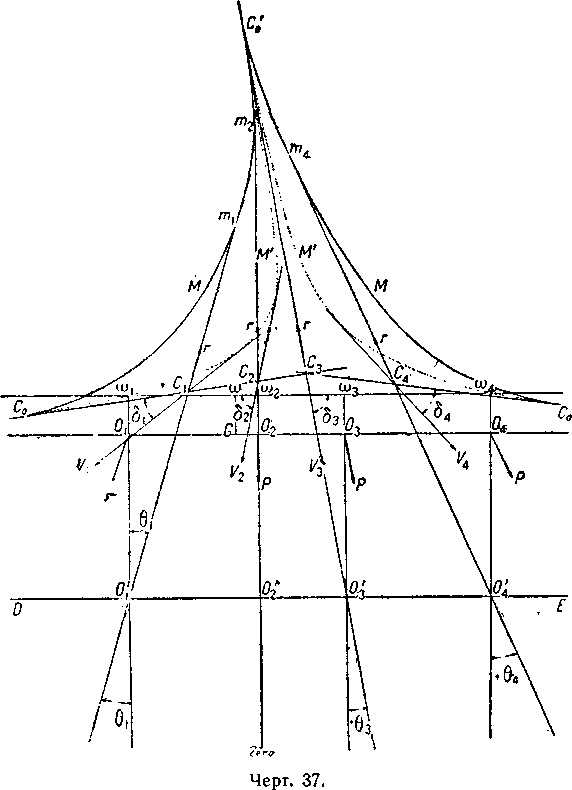
Все эти положения равновесия, повернутые таким образом, чтобы направление силы сопротивления воздуха было вертикальным, дают положение корабля при равновесии в пространстве и определяют направление его движения.

Изучение равновесия дирижабля при одновременном действии силы тяги и вертикальных сил

Общий случай

Для уточнения этого вопроса мы воспользуемся работой морского инженера Радиге, относящейся к отдаче предохранительных грузов подводной лодки „Опал“. Так как Радиге рассматривал лишь один частный случай, то нам пришлось переработать его труд, чтобы дать возможность применить этот метод к общему случаю и к полету дирижабля.

Рассмотрим дирижабль в равновесии при нулевом диференте, при нулевой сплавной силе.

Приложим силу тяги π, направленную по ТТ′ и дадим хлопок клапана силы р в ω₁ (чертёж 38).

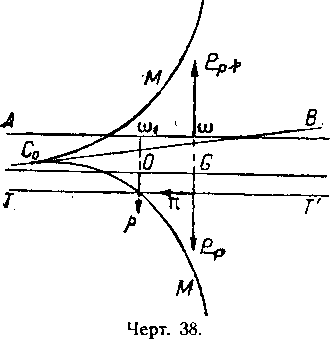
Это равносильно приложению в О силы р со знаком минус к аэростату, восстанавливающая пара которого будет (Р−р)·α.

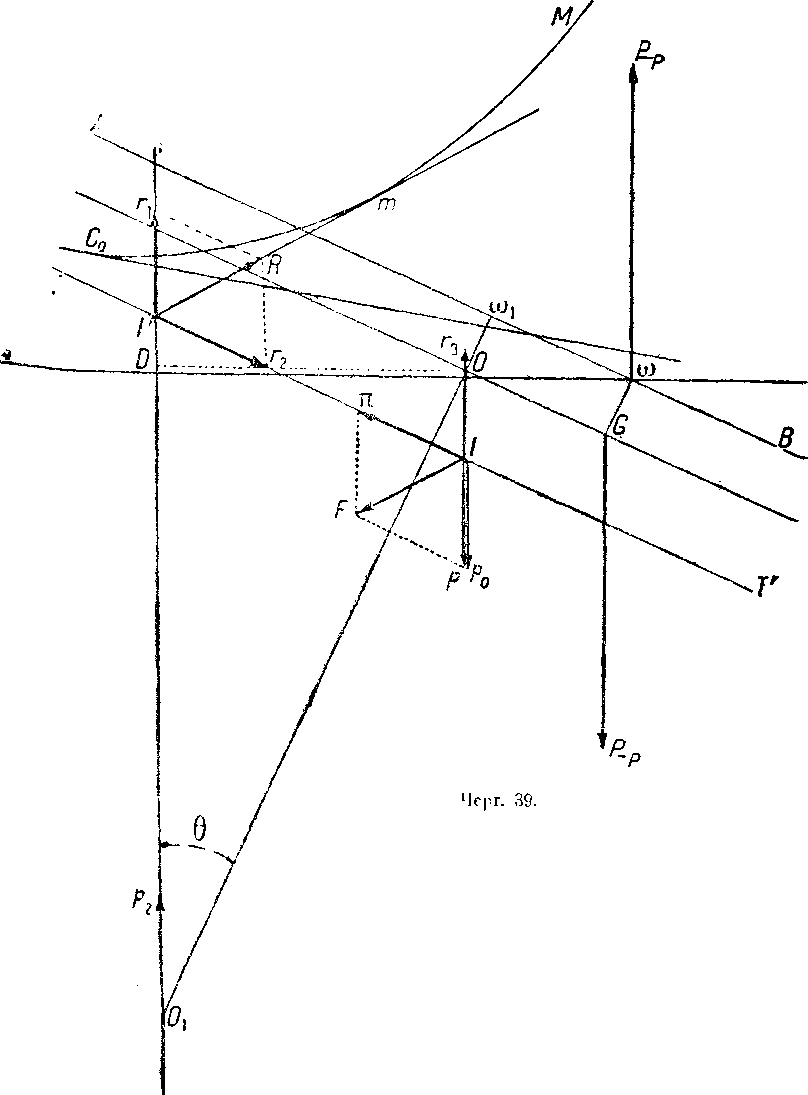
Под действием этих двух сил корабль приходит в движение, производит эволюции и устанавливается в положении равновесия, когда движение будет прямолинейным и равномерным (постоянная скорость, постоянный диферент). Пусть θ будет углом диферента при равновесии (чертёж 39). I является центром возмущения, и мы имеем приложенную в нем силу IF, параллельную силе сопротивления воздуха, причем последняя является касательной к метацентрической кривой.

Рассмотрим составляющие этих двух сил.

Мы имеем:

I_π=I′r₂.

Сила I′r₁ может быть заменена равной ей силой I′r₃и парой r₁I′Ip₀; Ir₃=I_p. Таким образом имеем равновесие сил.

Пара r₁I′Ip₀ представляет собою динамическую опрокидывающую пару, и равновесие пар дает:

Пара r₁I′Ip₀= (Р−р)·α·sin θ.

Из точки О проведем прямую, перпендикулярную к направлению линии нулевого диферента АВ. Эта прямая в точке О₁ пересекается с вертикалью, проходящей через точку I′. Приложим к этой точке две силы, равные р и прямо противоположные. Это обстоятельство ничего не меняет в условиях равновесия; можно считать, что сила р₁ является результирующей сил Р−р, приложенной в ω, Р−р, приложенной в G, и р, приложенной в О.

Действительно мы имеем:

пара pODp₂= паре p₂×OD,

р₂×OD=p₁×ОО₁·sin θ=(Р−р)·α·sin θ.

Три вертикальных силы: Р−р, Р−р, р, могут быть заменены силой Р₁, приложенной в О₁, и условия равновесия будут следующие:

Iπ=I′r₂, I′r₁=р₁=р.

Таким образом мы имеем теперь дело лишь с двумя силами π и р₁, и когда равновесие будет достигнуто, то сопротивление воздуха, касательное к метацентрической кривой, будет прямо противоположно результирующей этих двух сил. С другой стороны, положение точки О₁ определено уравнением:

р×ОО₁·sin θ=(Р−р)·α·sin θ, откуда,

ОО1=	P−p	·α
	p

причем точка О₁ является определенной.

Задача теперь сводится к следующему: имея корабль, представленный своими характеристическими кривыми,

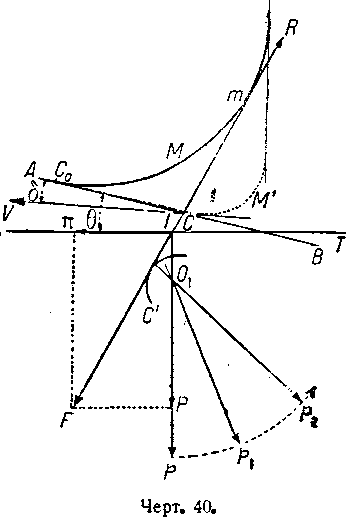
определить его положение равновесия в пространстве, когда к нему приложены сила тяги π, направленная по ТТ′, и вертикальная сила р, проходящая через определенную точку О₁, (чертёж 40).

В общих чертах эта проблема равновесия самолета, перемещающегося в условиях прямолинейного и равномерного движения. В этом случае сопротивление воздуха прямо противоположно результирующей приложенных сил (тяги и веса).

Возьмем дирижабль в состоянии равновесия, перемещающийся прямолинейно и равномерно с углом диферента θ.

Приложенные силы будут: сила тяги π, направленная по ТТ′ и имеющая определенный угол с направлением линии нулевого поддержания; сила р, приложенная в О₁ и направленная по вертикали. В точке I — точке приложения результирующей сил в рассматриваемом равновесии мы имеем две равные силы: IF=CR, которые прямо противоположны.

Сохраняя направление ТТ′ неизменным в пространстве, будем поворачивать силу р на 360° вокруг точки О₁. Каждому положению р будет соответствовать определенное положение результирующей π и р.

Проведя огибающую направлений этих результирующих, мы получим кривую С′. Касательная, общая к этой кривой С′ и метацентрической кривой, даст нам направление сопротивления воздуха в отыскиваемом равновесии, а также ее положение относительно направления линии нулевого динамического поддержания.

Определяя далее величину диферента, мы будем иметь возможность ориентировать корабль в пространстве по отношению к горизонтальному направлению, а проведя из центра девиации при равновесии касательную к кривой девиации, мы получим направление движения.

Отыскание кривой С′.

Пусть π будет тягой, направленной по ТТ′ (чертёж 41); I является центром возмущения и Iр—направлением силы р, проходящей через точку О; так как I является точкой приложения сил, то возьмем Iр=р, причем IF является результирующей р и π.

Из точки F опустим перпендикуляры FО′ и FА′ на направления Iр и ТТ′, и из точки О восставим перпендикуляр ОЕ к Iр.

Из точки Е прямой IF опустим перпендикуляр на направление ТТ′.

Имеем:

ЕА	=	IE	=	EO
FA′		IF		FO′

откуда

ЕО	=	FO′
EA		FA

Но площадь IπF= площади IFp, или

π×FA′=p×FO′; следовательно имеем:

EO	=	FO′	=	π	=const
EA		FA′		p

Следовательно, точка Е расположена на коническом сечении, фокусом которого является точка О; направление тяги ТТ′—его директриссой, а отношение

π	—его эксцентриситетом (чертёж 42)
p

Следовательно, прямая, которая соединяет точку пересечения I касательной к коническому сечению и директриссы с фокусом, то есть прямая

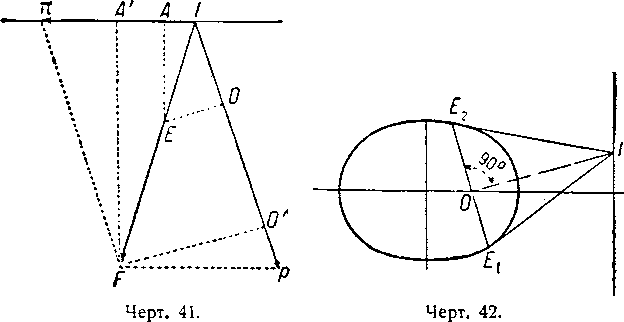
IO, является перпендикулярной к прямой, соединяющей фокус с точкой касания, то есть IO перпендикулярна к ЕО ( чертёж 42).

В этих условиях местом расположения точки Е будет коническое сечение, для которого точка О является фокусом, направление тяги—директриссой и отношение

π	— эксцентриситетом
p

С другой стороны, результирующая сил π и р, касательная к метацентрической кривой и проходящая через точку I, является касательной в точке Е к коническому сечению, которое только что определено; это коническое сечение (кривая С′) является огибающей результирующих

которую можно получить, поворачивая силу р вокруг точки О; при этом направление ТТ′ тяги остается неизменным.

Так как мы не допускали каких-либо гипотез касательно относительных величин р и π, то следующие данные приложимы ко всем случаям

сила тяги моторов меньше р₁—в этом случае С′ представляет собою эллипс; сила тяги моторов равна р,—в этом случае кривая С′ представляет собою параболу; сила тяги моторов больше р,—в этом случае кривая С′ представляет собою гиперболу.

При полетах дирижаблей эти три конических сечения будут использованы для отыскания положений равновесия, соответствующих силам, нарушающим равновесие, встречающимся в навигационной практике.

Отыскание положения равновесия дирижабля в движении, когда нарушение равновесия вызывается хлопком клапана, приложенным в центре объёма газовой массы.

Возьмем дирижабль с характеристическими кривыми М и М′ при нулевом диференте и нулевой сплавной силе в состоянии покоя.

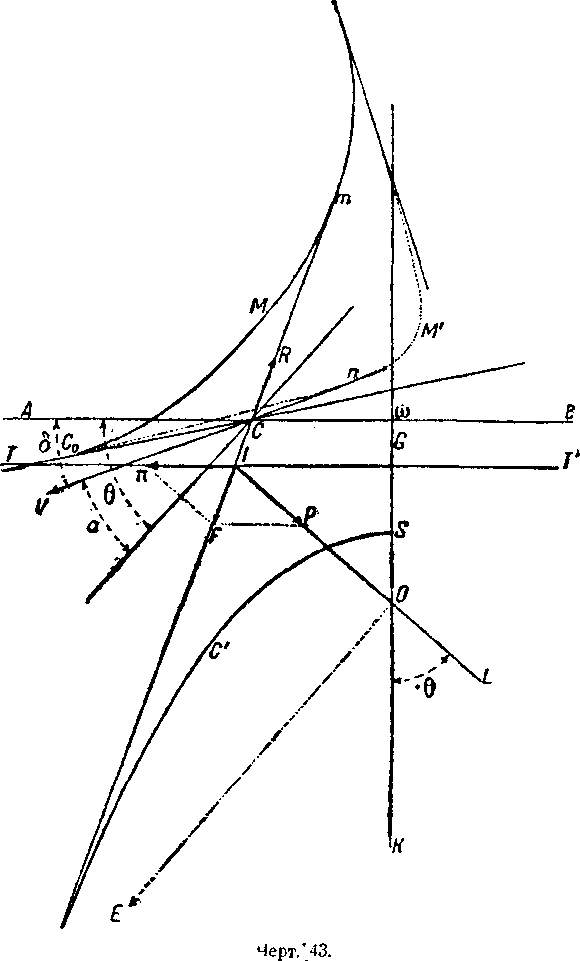
Приложим по направлению тяги ТТ′ силу тяги моторов π и дадим хлопок клапана силы р в ω—центре объёма газовой массы (центральный газовый баллон) (чертёж 43).

Пусть вес дирижабля равняется 10 тонн и пусть р утяжеление, вызванное хлопком клапана в центре объёма газовой массы, будет равно 1 тонне. Величина тяги, действующей по направлению ТТ′, также равняется 1 тонне.

Мы видели, что точкой приложения силы р должна быть точка G — центр тяжести, и что вследствиехлопка клапана восстанавливающая пара будет:

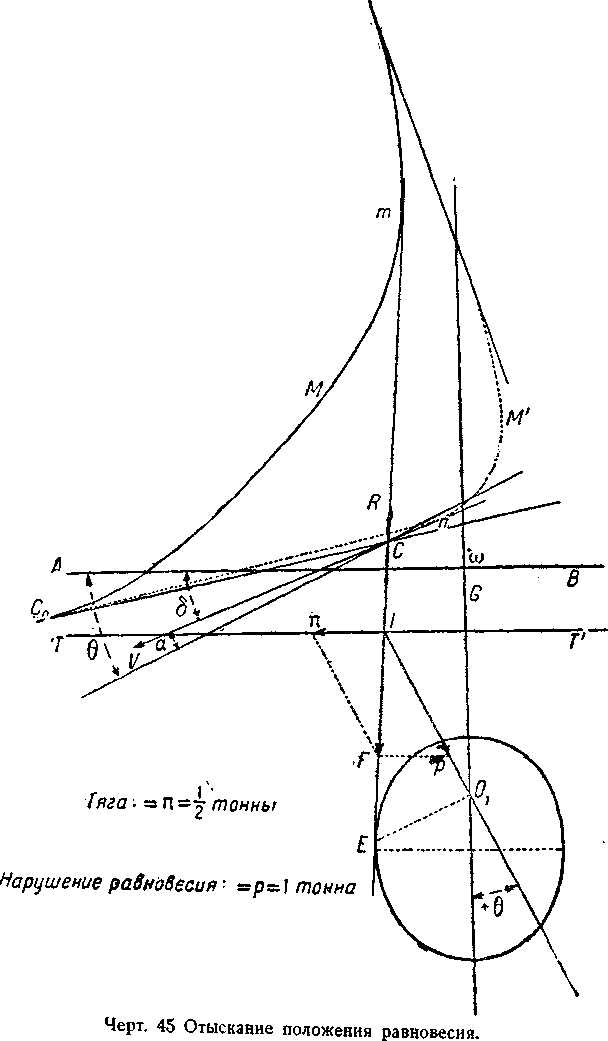
Чертёж 45 Отыскание положения равновесия.

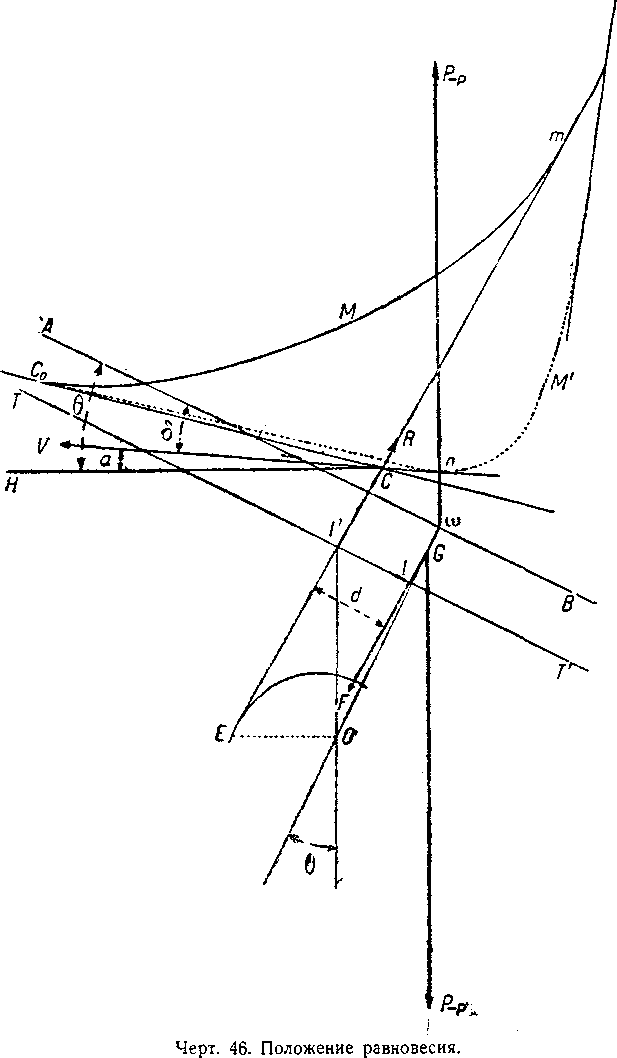
Чертёж 46. Положение равновесия.

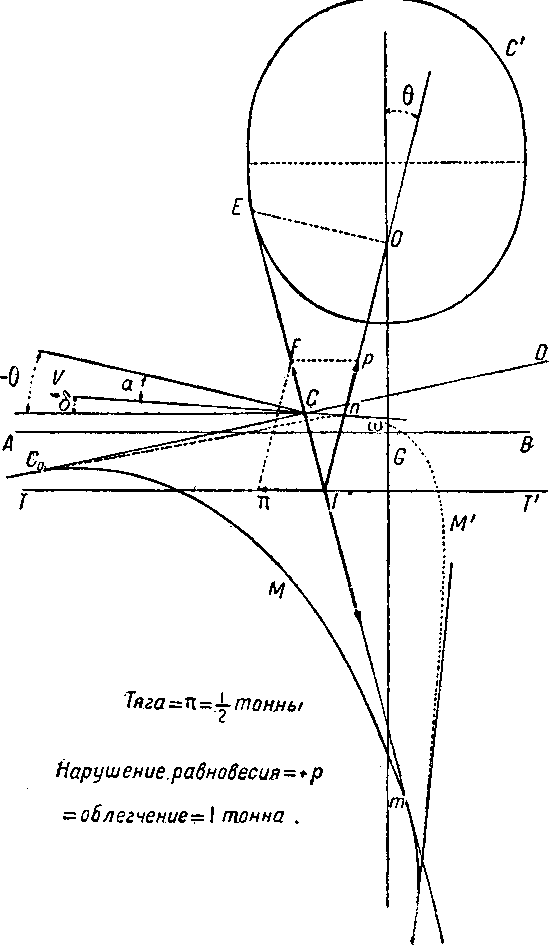
Чертёж 47. Отыскание положения равновесия.

(Р−р)·α=(10—1)·α=9·α.

в данном случае

Расстояние до фокуса конического сечения, которое является параболой, будет:

Р−р	·α=	9·α	=9·α
p		1

считая книзу от центра тяжести G.

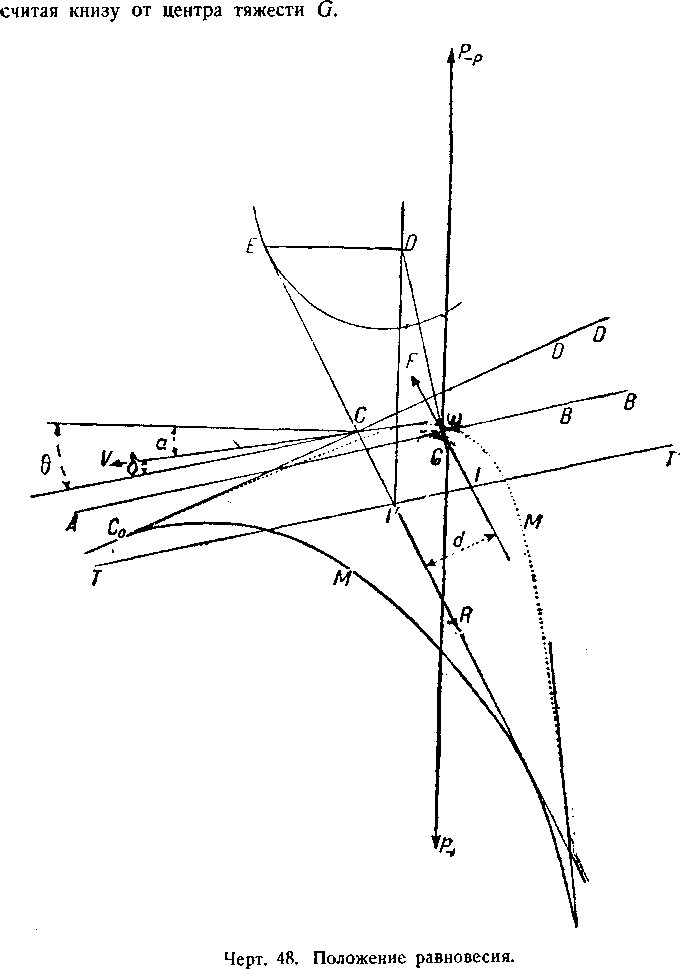
Пусть О будет этой точкой. Построим параболу, имеющую своим фокусом точку О и директриссой направление TT′. Этой параболой будет кривая С′. Проведем касательную, общую этой кривой и метацентрической кривой; мы получаем Im—положение силы сопротивления воздуха при равновесии.

Соединяя точку I с точкой О, мы получаем направление новой вертикали в этом равновесии, а величина диферента определяется углом КОL.

Через точку О проведем перпендикуляр к направлению IO, эта прямая пересекается с коническим сечением в точке Е, где его касается прямая, определяющая собой направление силы сопротивления воздуха. Эта прямая ЕО в положении окончательного равновесия будет горизонтальной.

Проведя из точки С—центра девиации—касательную к кривой девиации М′, мы получим направление движения CV.

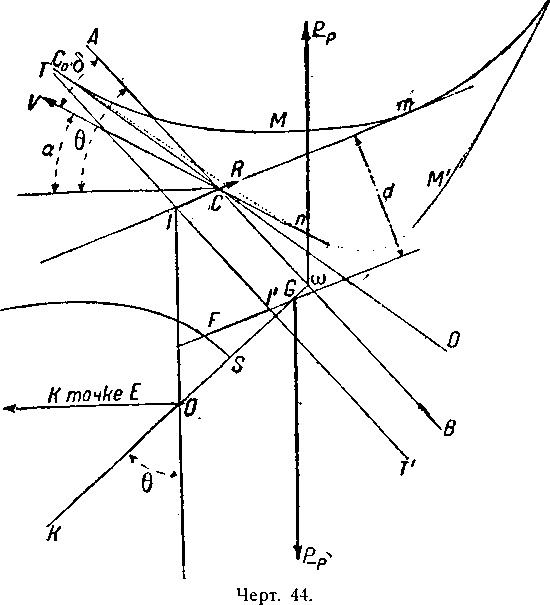
Теперь отстается лишь повернуть чертеж по направлению часовой стрелки на угол θ, ориентируя направление IO по направлению вертикали, и мы получим положение дирижабля в пространстве (чертёж 44).

На чертежах на страницах 34 — 38 мы даем построение для отыскания положения равновесия при различных относительных величинах силы тяги и силы, нарушающей равновесие. Все эти графики уже повернуты и дают для каждого случая положение дирижабля в состоянии равновесия при прямолинейном и равномерном движении (чертёж 45, 46, 47, 48 и 49).

Эти разнообразные построения дают нам значительные изменения угла диферента; это вытекает из того обстоятельства, что мы выбрали характеристические кривые с таким расчетом, чтобы изображения были бы в достаточной мере выявлены. Реакции подвергаются рассмотрению главным образом с качественной стороны; например, мы замечаем, что отклонения в величине диферента при утяжелении будут больше, чем при аналогичном облегчении; это обстоятельство является следствием воздействия момента от тяги моторов.

Хлопок клапана в каком-нибудь газовом баллоне

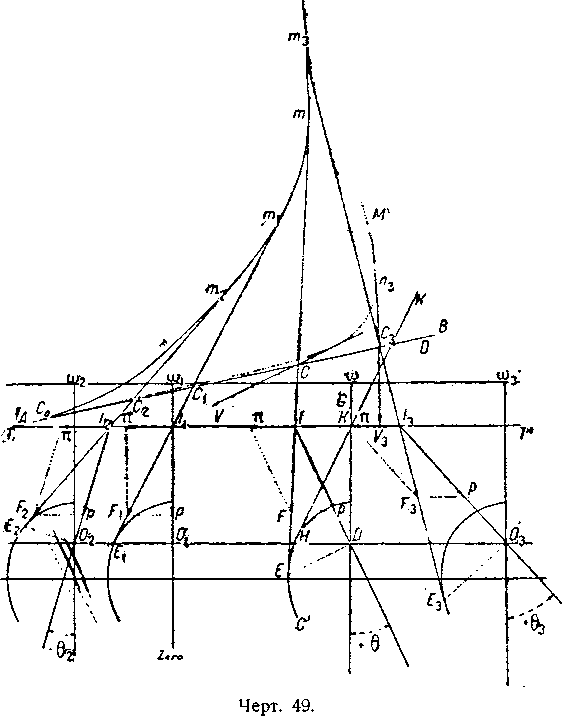
Пусть М и М′ будут характеристическими кривыми дирижабля, а АВ направлением линии нулевого поддержания, когда аэростат находится в равновесии в состоянии покоя при нулевом диференте; ω будет центром объёма, a G центром тяжести (четр. 49).

Найдем коническое сечение, характерное для тяги

p

2

допуская, что дирижабль весом 10 тонн р=1 тонна, а тяга равна 0,5 тонн

Коническое сечение представит собою эллипс С′, причем точка О является фокусом этого эллипса; построение графика равновесия дает нам диферент +θ для хлопка клапана в центральном баллоне в ω.

Давая хлопок клапана в одну тонну в произвольной точке корабля, мы замечаем, что директриссой будет всегда направление тяги и что эксцентриситет, равный —

π

p

всегда постоянен. Следовательно, достаточно переместить коническое сечение, чтобы сейчас же получить угол диферента при равновесии для хлопка клапана в любой точке.

Мы можем определить точку ω₁ для которой положение равновесия будет при нулевом диференте.

При равновесии прямая, соединяющая фокус с точкой касания, будет горизонтальной; следовательно, проведя прямую НК, являющуюся касательной к коническому сечению, мы получаем направление сопротивления воздуха для отыскиваемого положения равновесия.

Проведем линию, параллельную к этой прямой, касательную к метацентрической кривой. Эта прямая пересечется с линией тяги ТТ′ в некоторой точке I₁, являющейся центром напора. Проводя из точки I₁ перпендикуляр к направлению линии нулевого диферента, мы имеем в ω₁ точку, где должно быть вызвано нарушение равновесия для получения нулевого диферента, поскольку О₁ является фокусом конического сечения.

Для всех хлопков клапанов, приложенных спереди от точки ω₁, углы диферента при равновесии будут отрицательными; они будут положительными для всех точек, расположенных сзади ω₁.

Действительно, мы имеем диферент — θ₂, для хлопка клапана в ω₂ и диференты +θ и +θ₃—для хлопков клапана в ω и ω₃.

Изменения величины диферента и высоты полета, являющиеся следствием непостоянства общего веса корабля во время полета

Приведенные в начале этой работы опыты дают нам представление о реагировании корпуса жесткого дирижабля, идущего с данной полетной скоростью, на изменение общего веса аэростата из-за солнечной радиации или вследствие возникновения разницы в температуре воздуха и газа.

Пользуясь только что изложенным методом исследования вопроса и для данного случая, мы установим соответствие результатов, к которым нас приводит этот метод, с опытными данными, полученными во время полета.

Это теоретическое исследование будет произведено в отношении корабля, имеющего ось симметрии, в котором, кроме того, направление тяги совпадает с осью; это делается для упрощения графического изображения положений равновесия и для придания большей ясности чертежам.

Характеристические кривые будут относиться к дирижаблю в 10 тонн, предполагаемому выполненным при нулевой сплавной силе и уравновешенным в состоянии покоя при нулевом диференте.

Приложим по оси силу тяги, равную, например, 1 тонна и будем отыскивать положение равновесия, соответствующее последовательным утяжелениям в 0,5, 1 и 2 тонны, приложенным в центре объёма газовой массы для случаев, когда имеется различие в температуре воздуха и газа.

Это равносильно изучению случая, имеющего место во время обычного полета дирижабля, который следует с определенной скоростью и мало по-малу утяжеляется с увеличением разницы в температуре воздуха и газа.

1. Тяга равна одной тонне. Утяжеление равно 500 килограмм.

Это равносильно приложению веса в 500 килограмм в центре тяжести аэростата, восстанавливающая пара которого будет (Р−р)·α.

Расстояние по высоте до фокуса конического сечения О_1; считая от центра тяжести, будет (чертёж 50):

P−p	·α=	9,5	·α=19α
p		0,5

Так как отношение

π

p

больше единицы, то коническое сечение представляет собою гиперболу, точка О₁ является одним из ее фокусов, а ось аэростата, совпадающая с направлением тяги,— директриссой. Эта гипербола имеет своей вершиной точку S₁, а одной из ассимптот—прямую KL.

Общая для этого конического сечения и метацентрической кривой касательная m₁C₁ определяет положение силы сопротивления воздуха и центра девиации C₁ Направление O₁C₁ является направлением вертикали в отыскиваемом положении равновесия при диференте +θ₁, и С₁ V₁определяет собою направление движения.

Это построение вполне правильно, так как обе силы С₁р₁ и С₁π дают результирующую силу С₁ F₁касательную к метацентрической кривой, а

С1р1=	π
	2

Достаточно повернуть чертеж, направив С₁О₁ по вертикали, чтобы получить положение дирижабля.

2. Тяга равна одной тонне. Утяжеление равно одной тонне (чертеж 50).

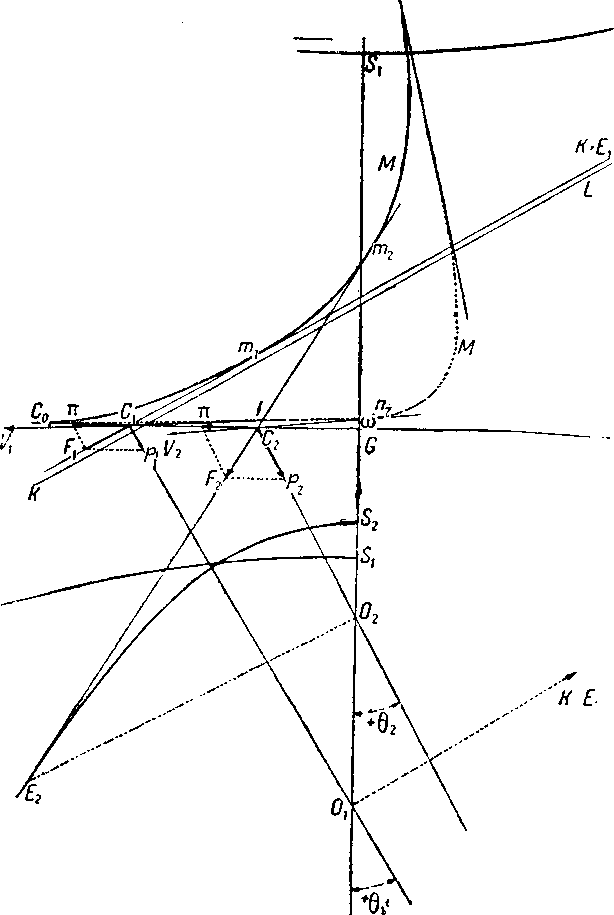
Чертёж 50.

Положение фокуса конического сечения по высоте, считая от центра тяжести, будет:

P−p	·α=	10−1	·α=9·α
p		1

Таким образом получаем точку О₂ в качестве фокуса параболы, вершиной которой будет точка S₂. Общая касательная дает положение сопротивления воздуха для центра девиации С₂, а направление О₂С₂ будет направлением вертикали в трм положении равновесия, которое должно наступить. C₂V₂ представляет собою направление движения. Диферент +θ₂.

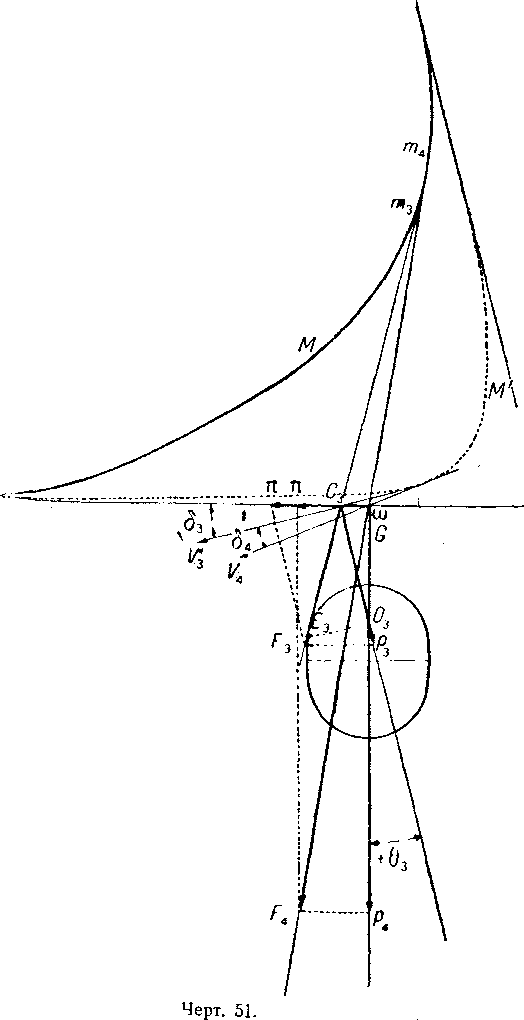
3. Тяга равна одной тонне. Утяжеление равно двум тоннам (чертёж 51). Положение фокуса эллипса по высоте определяется равенством:

P−p	·α=	10−2	·α=4α
p		2

восстанавливающая пара равна 8α.

Находим точку O₃; общая касательная С₃m₃ дает положение сопротивления воздуха, а направление С₃О₃—направление вертикали при равновесии, которое наступит при диференте +θ₃.

C₃V₃ представляет собою направление движения.

4. Не прибегая ни к какому коническому сечению, имеем одно положение равновесия, которое можно найти немедленно: то, которое соответствует нулевому диференту. Достаточно провести из центра объёма газовой массы касательную к метацентрической кривой, чтобы получить положение сопротивления воздуха в этом случае (чертёж 51).

Отыскивая вертикальную составляющую, соответствующую этому случаю равновесия, имеем в ωp₄ величину утяжеления; в этом случая р приблизительно равно 5,5 тонны.

Для утяжелений, превышающих эту величину, аэростат будет двигаться с опущенным носом, и предельная величина диферента найдется построением графика равновесия для случая, когда аэростат опорожнен, то есть когда р=Р.

Точка G является тогда фокусом эллипса. Построение графика этого равновесия весьма затруднительно вследствие близости точек G и ω; к тому же этот случай не представляет интереса с практической точки зрения.

Таковы реакции корабля. Мы брали корабль, обладающий осью симметрии, чтобы придать большую ясность изображениям; использование несимметричного корабля, в котором направление линии нулевого динамического поддержания отлично от направления оси, при тяге, прилагаемой снизу от оси, дало бы нам аналогичные результаты.

Для рассмотрения движений этого дирижабля нанесем на горизонтальную линию, начиная от некоторой исходной точки О, величины утяжелений, служившие для установления последовательных положений равновесия, и по оси координат отложим соответственные величины углов диферента и углов атаки. Соединяя друг с другом полученные таким образом точки, мы получим две кривые изменения величины диферента и угла атаки, когда утяжеление повышается непрерывно от 0 до предельной величины (опорожненный аэростат).

Рассмотрим лишь начальную часть этих кривых, соответствующую нормальным утяжелениям в условиях навигации. Кривая изображена здесь в увеличенном размере (чертёж 52).

Вертикальное расстояние на одной из ординат между этими двумя кривыми дает величину угла пути в вертикальной плоскости, которую мы можем нанести на другие оси (чертёж 53).

1. В В угол пути будет максимальным, причем от О до В, то есть для

утяжеления, меняющегося от 0 до 660 килограмм, положительный диферент увеличивается быстрее угла атаки. Эта фаза, характеризующаяся быстрым

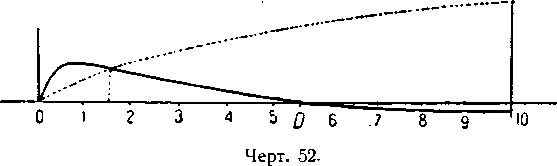
подъемом тяжелого дирижабля на полетной скорости, может быть названа „первичным режимом на подъеме“.

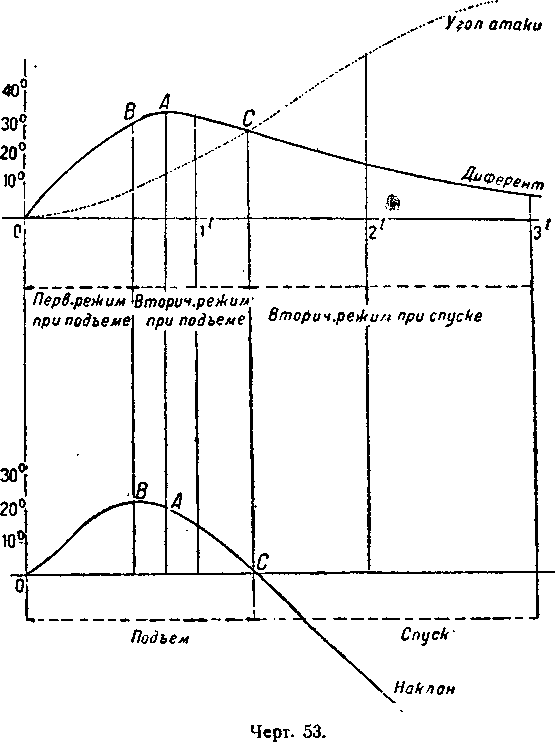
2. В А диферент будет максимальным для величины утяжеления в 840 килограмм. Эта максимальная величина угла диферента корабля соответствует максимальной величине динамической опрокидывающей пары.

В С угол диферента равен углу атаки и угол пути равен нулю для величины утяжеления в 1 300 килограмм. Здесь мы имеем максимальный вес, который корабль может нести (руль на нуле) по горизонтальной траектории при статической паре, определенной заданным начальным весом.

От В к А положительный диферент увеличивается менее быстро, чем угол атаки, а от А до С диферент уменьшается, а угол атаки увеличивается. Дирижабль поднимается по наклону, все мейее выраженному по мере того, как утяжеление увеличивается. Эта фаза может быть названа „вторичным режимом при подъеме“.

3. От этого момента (точка С), по мере того как утяжеление увеличивается, положительный диферент уменьшается, а угол атаки быстро увеличивается и оказывается больше, чем угол диферента, в связи с чем аэростат спускается с поднятым носом. Эта фаза может быть названа „вторичным режимом при спуске“.

4. Нулевой диферент получается в D для утяжеления в 5,5 тонны, и угол пути в этот момент равен углу атаки; далее диферент становится отрицательным, и угол пути равен сумме двух углов: диферента и атаки. Эта фаза не представляет интереса, так как она соответствует катастрофическим утяжелениям (чертёж 52).

Так как все дирижабли имеют характеристические кривые, аналогичные тем, которыми мы пользовались, то при движении они одинаково реагируют на изменения в весе, а степень реагирования зависит от формы корпуса и скорости пути.

Опыт показал, что реакции обнаруживаются более резко на жестких дирижаблях и, наоборот, они вовсе не были обнаружены на мягких. В связи с этим нам приходится изучать этот феномен для обоих типов дирижаблей раздельно.