> Дирижабли, страница 1 > Исследование условий равновесия воздушного корабля, двигающегося прямолинейно и равномерно

Исследование условий равновесия воздушного корабля, двигающегося прямолинейно и равномерно

Общие положения

Управляемый аэростат состоит из двух основных частей:

1. Удлиненного в направлении движения корпуса, содержащего в себе несущий газ, и
2. Одной или нескольких гондол, предназначенных для размещения людей, органов управления и моторов

Совокупность этих двух основных частей и образует воздушный корабль, который прежде всего должен обладать свойством сохранять устойчивое равновесие в обычном состоянии корабля. Это условие устойчивого равновесия будет выполнено, когда центр инерции, то есть центр тяжести массы, расположен ниже центра Объема газовой массы и на одной с ним вертикали.

Представим себе корпус корабля, статически уравновешенный с горизонтальной осью на высоте h (чертёж 1); тогда мы имеем Ф=Р.

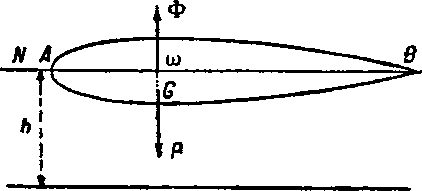
Чертёж 1.

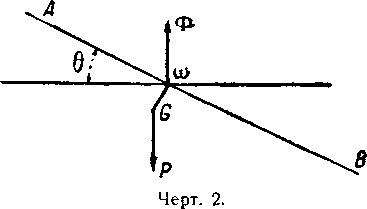
Так как центр тяжести массы G при горизонтальной оси корабля расположен под центром объёма газовой массы ω и на одной с ним вертикали, то равновесиедолжно быть устойчивым. Действительно, если отклонить ось корабля на угол θ (чертёж 2), то пара Р·а·sin θ (где а=ωG) стремится привести корабль в его первоначальное состояние равновесия.

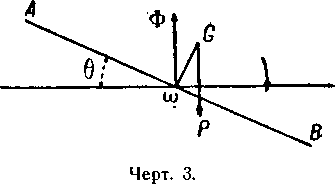
Если предположить обратное, то есть что центр тяжести массы расположен над центром объёма газа и на одной с ним вертикали, то хотя и будет иметь место равновесие, однако оно будет неустойчивым. Действительно, если в этом случае отклонить ось корабля на угол θ (чертёж 3), то пара Р·а·sin θ уже не стремится восстановить исходное положение, а, наоборот, стремится повернуть корпус аэростата до того положения, когда центр тяжести окажется уже под центром объёма газа, на одной с ним вертикали.

Таким образом видно, что при всех движениях корабля необходимо учитывать эту восстанавливающую пару, которая изменяется пропорционально синусу угла наклона¹; назовем эту пару парой статической устойчивости.

С другой стороны, данные какого-либо равновесия во время движения корабля зависят не только от приложенных сил, но и от формы корпуса², а отсюда возникает, следовательно, необходимость пользоваться таким методом исследования, который учитывал бы влияние этой формы.

Ввиду этого мы применим геометрический прием, используя для этого две кривые: 1) метацентрическую кривую, являющуюся огибающей всех направлений равнодействующих сил сопротивления воздуха, действующих на корабль при различных наклонах оси относительно направления движения, и 2) кривую девиации, представляющую собою огибающую йаправлений скоростей, соответствующих различным наклонам оси корабля относительно направления скорости.

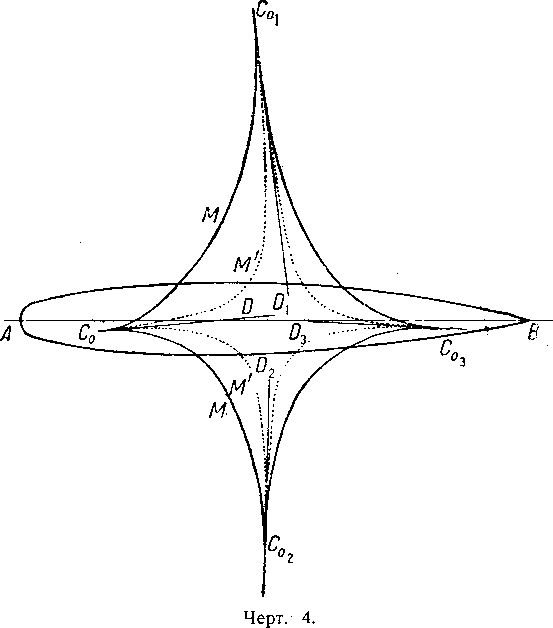
Эти две кривые будут являться характеристическими кривыми корабля (чертёж 4).

Для воздушного корабля данной формы (чертёж 4) и снабженного гондолой метацентрическая кривая как раз и имеет указанный здесь вид. Для случая поступательного движения она состоит из двух ветвей с точкой возврата С₀— главным центром девиации, и двумя другими точками возврата С₀₁ и С₀₂, значительно удаленными книзу и кверху.

Огибающая направлений скоростей М′, соответствующих различным углам атаки, имеет свои точки возврата, совпадающие с этими же точками метацентрической кривой. Кривую эту мы будем называть кривой девиации.

Верхняя передняя ветвь метацентрической кривой соответствует направлениям сопротивления воздуха, направленным снизу вверх, а следовательно—утяжелению корабля или, вообще, силам, направленным противоположно силам сопротивления.

Нижняя ветвь соответствует облегчениям или облическим силам тяги, направленным вверх.

При рассмотрении поступательного движения кривые эти обнаруживают три замечательных направления: C₀D, C₀₁D₁ и C₀₂D₂, касательные к кривым в точках возврата С₀, С₀₁ и С₀₂; для этих трех направлений направление скорости совпадает с направлением сопротивления воздуха; при этом направление C₀D представляется особенно интересным, так как оно соответствует нулевой силе динамического поддержания.

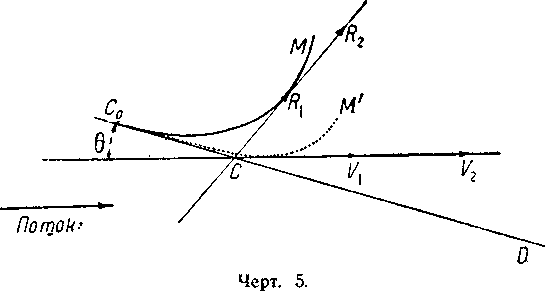
Наконец необходимо сделать замечание, имеющее большое значение с точки зрения динамики дирижабля и вытекающее из опытов в аэродинамической трубе: если рассмотреть в аэродинамической трубе поведение модели дирижабля, удерживаемой в воздушном потоке за какую-нибудь точку С линии нулевого динамического поддержания, то увидим, что под действием струи воздуха модель сама установится под таким углом θ, при котором направление сопротивления воздуха проходит через точку С и является касательной к метацентрической кривой; одновременно направление скорости, будучи горизонтальным, явится касательной к кривой девиации (чертёж 5). Точки, подобные точке С, называются центрами девиации.

Если увеличить скорость струи воздуха с величины CV₁ до величины CV₂, то сила сопротивления воздуха все равно будет проходить через точку С, и ее направление относительно направления линии нулевого поддержания останется неизмененным; лишь величина сопротивления увеличится с величины CR₁ до величины CR₂.

Мы можем сделать тот вывод, что в пространстве, когда направление сопротивления воздуха не изменяется относительно направления линии нулевого поддержания, то направление скорости остается неизменным и лишь величина скорости подвергается соответственному воздействию изменения облической тяги.

Теперь, когда мы имеем возможность учитывать влияние формы корпуса, остается установить, каковы движения корабля в вертикальной плоскости симметрии, иначе говоря, определить траекторию полета корабля в случае его прямолинейного и равномерного движения.

1 Как в данном случае, так и в дальнейшем под углом наклона корабля подразумевается угол наклона оси корабля к горизонту, или диферент.

2 Под приложенными силами, как оговорено вначале, автор имеет ввиду лишь силы тяги и вертикальные силы (возникающие вследствие маневрирования клапанами и балластом). Под зависимостью же условий равновесия от формы корпуса следует понимать влияние аэродинамических сил.