> Дирижабли, страница 1 > Начертание траектории корабля, перемещающегося прямолинейно и равномерно в вертикальной плоскости симметрии
Начертание траектории корабля, перемещающегося прямолинейно и равномерно в вертикальной плоскости симметрии
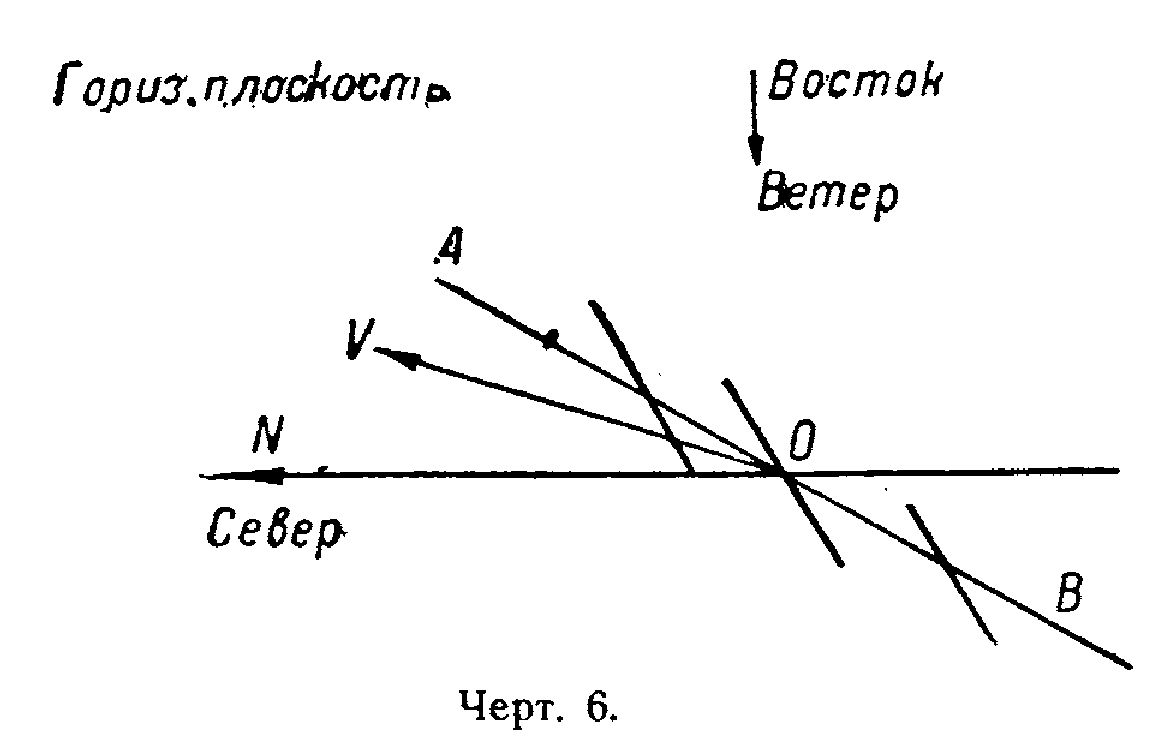
Рассмотрим сперва парусник, ориентированный относительно стран света, как указано на чертеже 6, и идущий под ветром, причем ветер дует с востока. Направление ветра рассматривается, как направление вредной силы, стремящейся нести корабль под ветром.
В результате воздействия подводной части судна, как показывает опыт, корабль поднимается по ветру, следуя направлению OV (чертёж 6), и мы имеем:
угол AON—курс,
угол AOV—дрейф (девиация),
угол VON — путь.
Зная курс и угол дрейфа, можно определить путь, то есть траекторию в горизонтальной плоскости.
Для этого требуется взять за начало отсчета углов два основных направления: 1) основное направление в корабле—ось; 2) основное направление для отсчета углов в пространстве—географический меридиан.
Когда корабль перемещается, следуя направлению своей оси, то направление скорости совпадает с направлением сопротивления потока и дрейф равен нулю. Мы сказали бы в этом случае, что корабль перемещается при прямом сопротивлении (чертёж 7).
Наоборот, когда направление скорости не совпадает с направлением сопротивления, то угол дрейфа имеет определенную величину. Наличие угла дрейфа как раз и характеризует облическое движение (смотрите чертёж 6).
Мы воспользуемся этим приемом для изображения траектории полета воздушного корабля в вертикальной плоскости, перемещающегося прямолинейно и равномерно.
Достаточно приподнять чертёж 6, чтобы получить положение поднимающегося отяжеленного дирижабля, причем направление силы веса является направлением вредной силы, стремящейся сопротивляться подъему корабля.
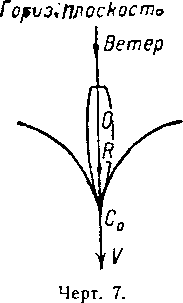
Возьмем за основание отсчета углов на корабле то направление1, для которого девиация равна нулю, то есть то направление, при котором сила динамического поддержания равна нулю; от этого направления и будем отсчитывать углы атаки.
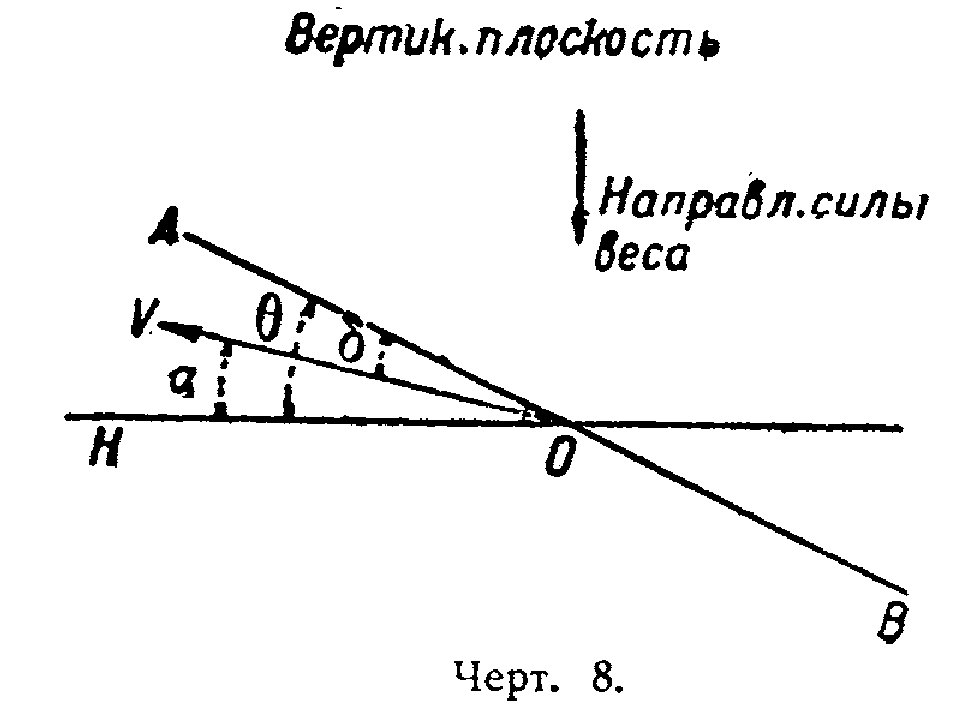
За основание отсчета углов в пространстве возьмем горизонтальное направление, и для случая прилагаемого чертежа (чертёж 8) мы имеем: угол АОН — угол наклона (диферент) или курс корабля в вертикальной плоскости — θ; угол AOV—угол атаки или угол девиации—δ; угол HOV—угол полета или путь корабля в вертикальной плоскости — α.
Эти три угла дают возможность представить себе все положения при подъеме и спуске, сопоставляя величины диферента и угла атаки.
(1 Совпадающее с направлением скорости)
Отяжеленный воздушный корабль
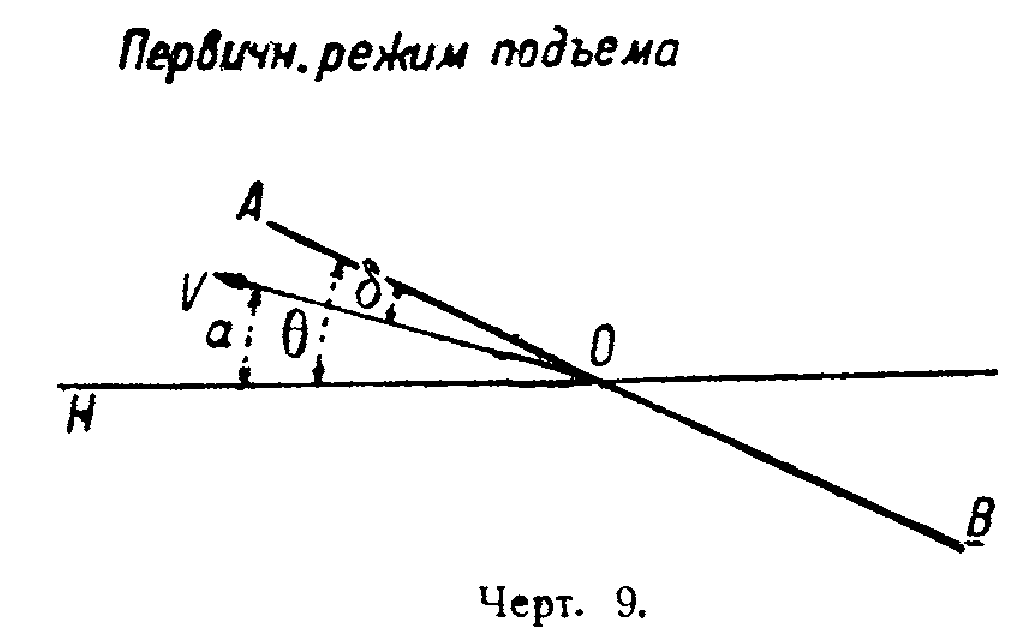
1. Подъем
Угол наклона корабля больше угла атаки.
Угол полета равен +α=+θ—δ (чертёж 9).
Первичный режим полета (большие скорости, малые углы атаки).
2. Горизонтальное движение
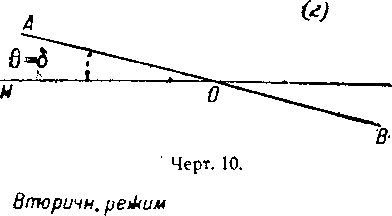
Угол наклона равен углу атаки: θ=δ.
Угол пути равен 0= +θ — δ (чертёж 10).
3. Спуск при положительном наклоне (с поднятым носом)
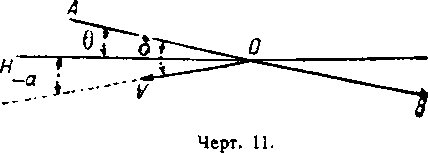
Угол атаки больше угла наклона корабля.
Угол пути равен — α=—δ+θ (чертёж 11).
Вторичный режим полета (малые скорости, большие углы атаки).
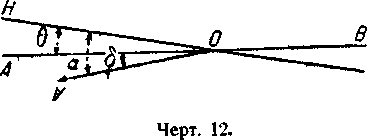
Быстрый спуск.
Угол наклона корабля добавляется к углу атаки.
Угол пути равен —а =—(θ+δ) (чертёж 12).
Первичный режим при спуске (большие скорости, малые углы атаки).
Облегченный воздушный корабль
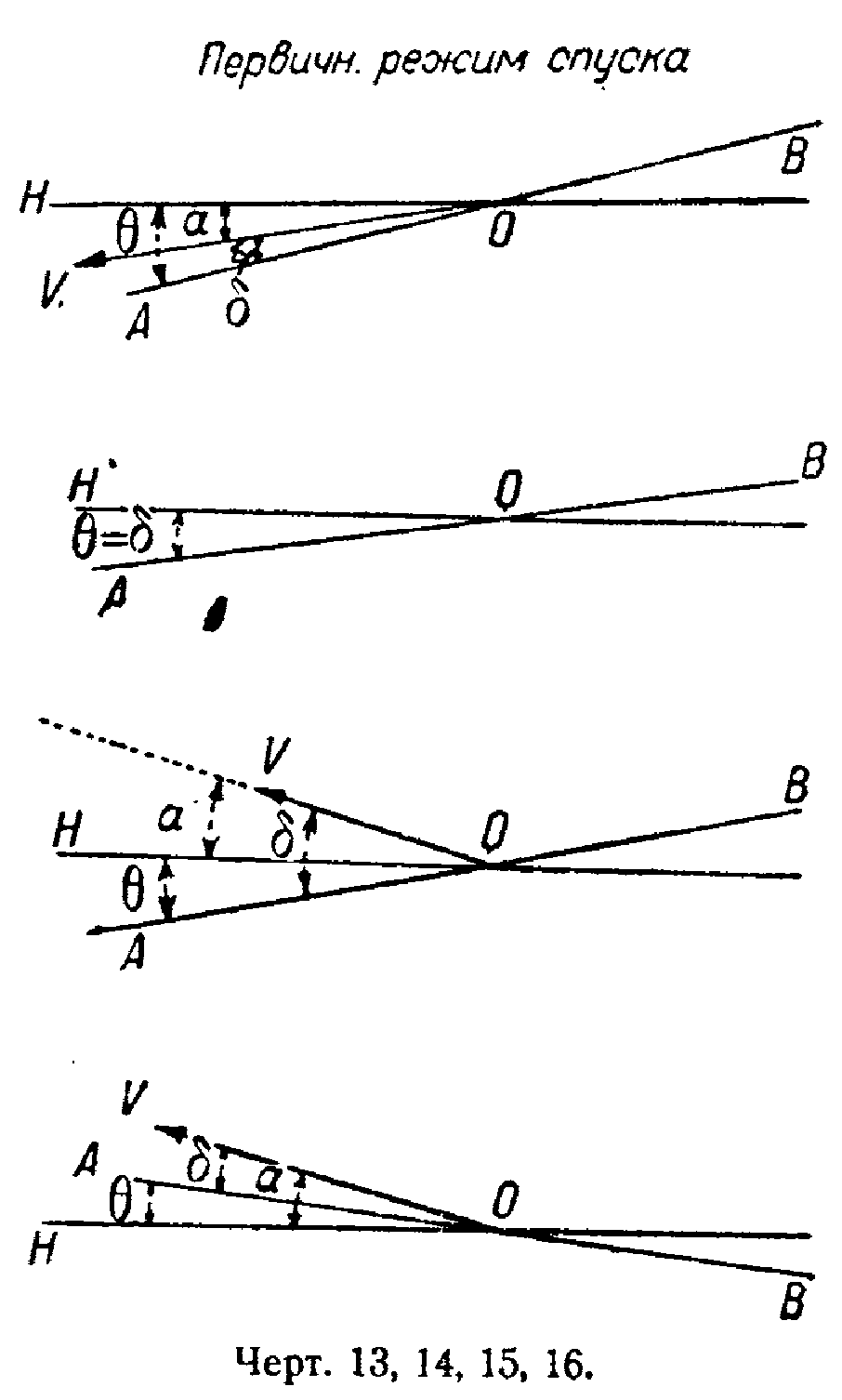
1. Спуск:
— a =θ+δ (чертёж 13).
2. Горизонтальный полет:
θ=δ
α=—θ+δ=0 (чертёж 14).
3. Полет с опущенным носом:
+α=+δ—θ (чертёж 15).
Вторичный режим полета.
4. Быстрый подъем:
+α=+θ+δ (чертёж 16).
Первичный режим полета при подъеме.
Когда дирижабль перемещается, следуя направлению нулевого динамического поддержания, то направление скорости совпадает с направлением сопротивления воздуха; это направление является касательной в точке возврата к характеристическим кривым. Угол атаки в этом случае равен нулю. Можно сказать здесь, что дирижабль перемещается при прямом сопротивлении.
Наоборот, когда направление скорости не совпадает с направлением сопротивления, то дирижабль перемещается путем облического движения. Это положение характеризуется наличием угла атаки или девиации; по этой причине мы и назвали огибающую направлений скоростей кривой девиации.
Для отсчета углов при исследовании полета в вертикальной плоскости мы взяли за основание отсчета углов в дирижабле направление линии ну левого поддержания. Диферент будет, следовательно, равен нулю, когда это направление горизонтально.
В навигационной практике для определения величины диферента служит направление оси корабля, а при спокойном состоянии корабль статически уравновешивается таким образом, что ось остается горизонтальной.
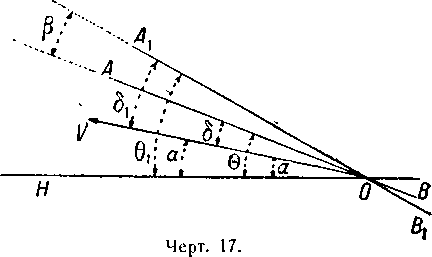
Следовательно, мы вынуждены взять эту линию за основание для отсчета углов в корабле, а вследствие этого теоретические углы, которые мы определили выше, будут отличаться на величину постоянного угла р, который является углом между направлением оси и направлением линии нулевого поддержания (чертёж 17).
Поскольку мы должны выполнить построение положений равновесия, мы будем пользоваться этими теоретическими углами, разумеется, с той оговоркой, что величина этих углов не будет служить нам для выражения величин сил или реакций, которые будут иметь место.
Теоретические (фиктивные) углы, которыми мы будем пользоваться беря ось за основание для отсчета углов, в корабле будут:
А1ОН—диферент, равный θ+β=01,
A1OV—угол атаки, равный δ+β=δ1.
Угол пути VOH не изменяется; лишь диферент и угол атаки изменяется на величину угла β. Наличие этого угла β ни в чем не изменяет применения метода, который будет дан для определения различных положений равновесия дирижабля, перемещающегося равномерным и прямолинейным движением.