 > Дирижабли, страница 1 > Поведение корабля на эксплуатационных скоростях
> Дирижабли, страница 1 > Поведение корабля на эксплуатационных скоростях
Поведение корабля на эксплуатационных скоростях
Мягкие дирижабли на полетной скорости
Рассмотрим кривые, представляющие собою изменение величин угла диферента и угла атаки мягкого аэростата, когда аэростат постепенно утяжеляется; укажем для определенных весовых соотношений в аэростате положение руля высоты, которое позволяет удерживать дирижабль на постоянной высоте, деформируя в каждый момент очертания корабля в целом1.
Следовательно, мы допускаем, что каждая точка этих кривых была получена при помощи метацентрических кривых, соответствующих каждому положению руля (чертёж 54).
В О руль на нуле. Сплавная сила равна нулю. Угол диферента равен нулю.
В О1, руль, например, повернут на 15° на спуск, диферент максимален; следовательно, придется использовать максимальный угол руля,′чтобы препятствовать подъему. Вес—ОО1.
В О2 руль снова на пуле. Вес—ОО2.
В О3, например, руль в положении „целиком на подъем“, и при рассматриваемой полетной скорости это положение будет соответствовать максимальному весу, который аэростат может нести в горизонтальном полете. Вес—ОО3.
1 Меняется положение руля
Таким образом мы видим, что для этого типа дирижаблей весь первичный режим при подъеме легко охватывается рулем высоты, причем угол поворота руля не превосходит 15°.
Это обстоятельство связывается с тем фактом, что на аэростатах этого типа статическая восстанавливающая пара относительно больше, чем на жестких кораблях, так как гондола расположена значительно ниже газового баллона.

Чертёж 54.
Сверх того площадь рулей глубины составляет более значительную часть всей площади оперения, чем на жестких кораблях. С другой стороны, скорости этих аэростатов обычно ниже 100 км/час.
В этих условиях, поскольку не было произведено опытов при руле, установленном на нуле, не было отмечено и случаев подъема тяжелого аэростата.
Жесткие воздушные корабли на полетной скорости
Рассмотрим кривые изменений величины диферента и угла атаки, полученные в тех же условиях с учетом поворота руля для каждой точки.
В О руль на нуле, например, для нулевой сплавной силы (чертёж 55). При утяжелении О1 руль стоит уже „полностью на спуск“ на полетной
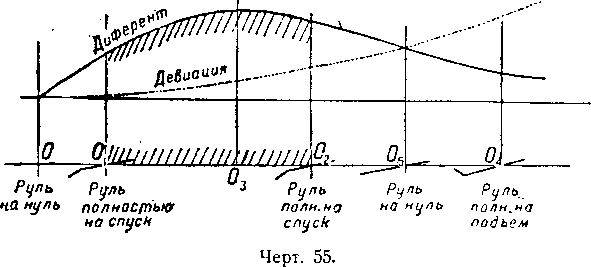
скорости; следовательно, после того как утяжеление перешло от нуля к О1 в распоряжении командира для сохранения постоянной высоты не остается ничего кроме моторов и балласта.
С другой стороны, при утяжелении О3 руль стоит на нуле на полетной скорости. Следовательно, между точкой, где диферент максимален, и утяжелением О3 существует утяжеление, в отношении которого командир вновь получает свободу распоряжения своим рулем. Пусть О2 будет величиной этого утяжеления.
Наконец, для утяжеления О4 руль стоит „полностью на подъем“, и это утяжеление соответствует максимальному весу, который аэростат может нести при полетной скорости.
Из этого положения явствует, что по мере того, как утяжеление нарастает с величины О1 до величины О2, аэростат поднимается при руле, установленном „полностью на спуск“, и что высоту можно удержать постоянной лишь при помощи тщательного маневрирования моторами и балластом. В течение всего этого периода линия очертания всего корабля не изменяет своей формы, так как руль застопорен „полностью на спуск“.
Маневрирование при помощи моторов
Мы должны полагать, что в О, О1 и O3 моторы отрегулированы на эксплуатон-ную скорость. Так как интересующий нас динамический эффект происходит вследствие того, что изменение диферента больше изменения угла атаки, то работа моторов будет прогрессивно уменьшаться, начиная от утяжеления О1 до того момента, когда динамическая опрокидывающая пара будет максимальной, что соответствует утяжелению О5.
Предположим, что при полетной скорости моторьг делают 1 000 об/мин и что для утяжеления О5 число оборотов, позволяющее держаться на постоянной высоте, будет 800; здесь можно прийти к выводу, что весь первичный режим будет поглощаться рулем при ходе на 800 оборотах. При превышении 800 оборотов реакции корпуса корабля таковы, что аэростат будет подниматься, и скорость подъема будет тем заметнее, чем более высокой будет полетная скорость.
Начиная от утяжеления О5, число оборотов будет прогрессивно увеличиваться, и для утяжеления О2 можно будет вернуться к полетной скорости.
2. Маневрирование балластом при сохранении полетной скорости
Поскольку аэростат стремится подняться в О1, так как он утяжеляется, необходимо устранить причину подъема, сбрасывая балласт таким образом, чтобы сохранить постоянной высоту.
Когда утяжеление перестает возрастать, командир вновь обретает свободу распоряжения своим рулем, сбрасывая сверх того соответственное количество балласта.
Мы рассмотрели случаи утяжеления; что же касается облегчения, то здесь принимаются обратные меры—работают клапаном; но все же и здесь действительной мерой является уменьшение скорости.
Геометрическое построение положений равновесия корабля при изменяющемся весе и движении позволяет, следовательно, выявить эти реакции и установить, что наблюдавшееся явление подъема тяжелого аэростата и спуска легкого не заключает в себе чего-либо парадоксального.
Нужно думать, что на практике затруднительно быстро уяснить, что происходит с весом корабля и, в связи с этим, требуемый маневр не вырисовывается с достаточной ясностью.
На практике наоборот, весьма легко, учитывая положение аэростата, знать в каждый данный момент, является ли аэростат легким или тяжелым, или очень легким или очень тяжелым.
Для управления на постоянной высоте, когда аэростат, например, утяжеляется, необходимо удерживать аэростат носом кверху, а когда аэростат облегчается, его необходимо удерживать носом книзу. Следовательно знак диферента, то есть положение носа аэростата в вертикальной плоскости, и дает необходимое указание для определения значения изменения веса.
Далее положение руля даст возможность установить эту величину изменения веса, для того чтобы узнать, является ли аэростат тяжелым или легким, или очень тяжелым или очень легким.
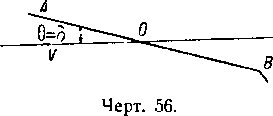
Чертёж 56.
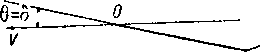
Чертёж 57.
Положение 1. Нос кверху, руль „полностью на спуск“; аэростат, будучи тяжелым, стремится подняться (чертёж 56).
Маневр, подлежащий выполнению: уменьшить ход или сбросить балласт для сохранения постоянной высоты.
Положение 2. Нос кверху, руль „полностью на подъем“ при стремлении к спуску. Аэростат очень тяжел (чертёж 57).
Маневр, подлежащий выполнению: увеличить ход или сбросить балласт для сохранения постоянной высоты.

Чертёж 58. Чертёж 59.
Положение 1. Нос книзу, руль „полностью на подъем“ при стремлении к спуску. Аэростат легок (чертёж 58).
Маневр, подлежащий выполнению: уменьшить ход или работать слегка клапаном, чтобы сохранить постоянной высоту.
Положение 2. Нос книзу, руль „полностью на спуск“ при стремлении к подъему. Аэростат очень легок (чертёж 59).
Маневр, подлежащий выполнению: увеличить скорость или работать клапаном для сохранения постоянной высоты.
Следовательно, мы видим, что знак угла диферента и положение руля высоты дают на этот счет очень надежные показания.
В начале этой работы мы сделали несколько допущений:
1. Характеристические кривые корабля предполагались известными
Чтобы пользоваться на практике этим методом рассмотрения, необходимо знать характеристические кривые корабля. Следовательно, необходимо произвести известное число опытов, чтобы определить их со всей возможной точностью. Ошвартовывая аэростат у причальной мачты в свободном состоянии при установившемся ветре и пользуясь специальным механизмом для измерения вертикальных и горизонтальных усилий тяги в потоке, ветра, можно будет получить ряд данных о силах сопротивления воздуха, соответствующих углам атаки, например, от 0 до 10°.
Этот способ, даст первое приближение формы кривых и их положении.
Далее придется уже в полете произвести новый ряд опытов на различных скоростях, для того чтобы установить, каково влияние воздушных струй от винта на форму этих кривых и их положение.
Сравнение этих кривых с кривыми, полученными в трубе и у причальной мачты, могут дать ценный материал для изучения будущих форм корабля.
2. Аэростат предполагался выполненным, то есть α постоянно
Так как основная цель этой работы указать со всей возможной ясностью геометрическое построение положений равновесия, то мы предполагаем а постоянным, для того чтобы облегчить построение чертежей.
При действительных операциях пришлось бы, разумеется, после каждого хлопка клапана или при каждом опыте вводить точную величину α, для каждого случая соответствующую: α1, α2, α3 и так далее.
3. Изменение веса, в связи с изменением аэростатом высоты
Когда аэростат меняет свою высоту, то газ либо сжимается, либо расширяется—в зависимости от движения вверх или вниз; к тому же температура окружающего воздуха значительно изменяется. В этих условиях наблюдается расхождение в температурах воздуха и газа, что влечет за собой изменение веса аэростата. Следовательно, в этих случаях мы имеем действие новых сил, которые дают новое положение корабля при равновесии.
Лишь опыт позволит установить, в какой мере этот метод исследования может быть пригоден, во-первых, для нахождения нового положения равновесия, когда значение и величина изменений веса известны, и, во-вторых, в том случае, когда величина изменений веса определяется положением равновесия, полученным на данной высоте.
4. Поскольку положение равновесия аэростата зависит от приложенных к нему сил, необходимо, разумеется, знать величину этих сил: величину изменения веса и силы тяги винтов. Что касается скорости, то она будет измерена.
В общем, надлежит сделать ряд опытов, чтобы определить степень воздействия изменений веса на поведение корабля в горизонтальном полете; все же данный ′нами очерк дает весьма ясное представление о реакциях корабля и может служить отправной точкой для производства опытов, которые позволят улучшить поведение дирижаблей в полете, учитывая очень существенные изменения веса, с которыми придется иметь дело и которые никогда не смогут быть устранены.