> Техника, страница 70 > Perpetuum mobile

Perpetuum mobile

Perpetuum mobile, вечное движение, ложный с точки зрения современной науки принцип, согласно к-рому можно построить такой механизм, к-рый, будучи раз приведен в движение, сможет находиться в движении и даже совершать нек-рую полезную работу «вечно», то есть неограниченно долгое время, без заимствования энергии извне. Очевидно,

что принцип P.m.,понимаемый в таком именно смысле, противоречит принципу сохранения энергии (смотрите), одному из самых основных принципов современного точного естествознания, по которому энергия из ничего создана быть не может, а каждое определенное количество энергии какого-либо вида, в частности кинетической, может перейти только в соответствующее эквивалентное количество энергии другого вида. Т. к. каждый механизм без постоянного сообщения энергии извне обладает лишь вполне ограниченным запасом последней, к-рый постепенно расходуется как на преодоление вредных сопротивлений, так и на выполнение полезной работы, то механизм без постоянно действующего внешнего источника энергии должен по истечении определенного промежутка времени остановиться; продолжение же движения механизма после израсходования своего собственного запаса энергии означало бы получение энергии из ничего.

В теоретич. механике закон сохранения энергии вытекает, как теорема из основных уравнений (ур-ия Лагранжа) для всех случаев, когда уравнения связей не содержат времени в явной форме (склерономны). В противном случае (реономных связей, содержащих время в явной форме) нарушение принципа энергии, вообще говоря, не противоречило бы уравнениям механики. В частном случае сил, являющихся отрицательными частными производными по координатам от некоторой функции координат (смотрите Потенциал), принцип энергии принимает обычную простую форму независимости суммы кинетической и потенциальной энергии от времени. Принцип энергии рассматривается в физике как эмпирич. постулат, справедливый, как показывает опыт, при всех условиях и для любых механич. или немеханич. замкнутых систем.

Естественно,что до установления принципа сохранения энергии делались постоянно попытки (и со стороны людей науки) осуществить P.m. несмотря на то, что наиболее выдающиеся из них интуитивно постигали тщетность этих попыток. Наиболее ранней попыткой осуществления Р. т. является попытка Пьер-де-Маренкура использовать для этой цели магнитные силы, о чем он сообщает в своей рукописи, написанной в 1269 г. Несмотря на то, что еще Леонардо да Винчи (1452—1519), Кардан (1501—1576), Стевин (1548—1620), Галилей и др. считали невозможность осуществления Р. т. постулатом и делали на основе этого различные выводы в своих научных построениях, все же 16-й, 17-й и 18-й вв. полны попыток осуществить Р. т. Только по окончательном установлении в середине прошлого столетия принципа сохранения энергии Майером (1842),Джоулем (1843) и Гельмгольцем(1847) наука смогла точно обосновать невозможность Р. т. Несмотря на это и до настоящего времени продолжаются тщетные попытки добиться осуществления Р. т.

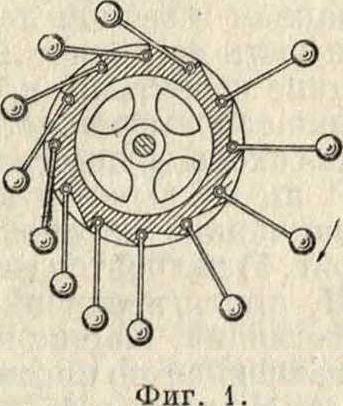
Наиболее часто используются свойства рычага, гидростатич. закон Архимеда, силы магнитного притяжения и т. д. Примерами могут служитьследующиепроекты конструкций. По внешней окружности колеса (фигура 1),

помещенного в вертикальной плоскости, прикреплены при помощи шарниров стержни равной длины с одинаковыми грузами, прикрепленными к их концам, причем с одной стороны колеса стержни висят под действием веса грузов, а с другой удерживаются в радиальном направлении зубцами. На первый взгляд кажется, что грузы последней стороны, находясь в общем на более отдаленном расстоянии от центра, чем грузы с другой стороны, должны перевешивать, вследствие чего колесо будет вертеться без сообщения работы извне. Более тщательное рассмотрение механизма показывает однако,что

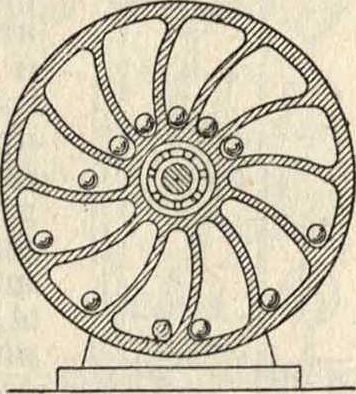
Фигура 2.

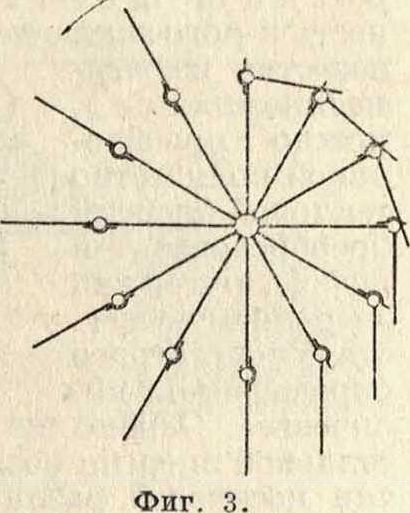
колесо, будучи выведено из состояния равновесия, должно будет остановиться вследствие того, что на стороне с более близкими к центру грузами последних окажется больше, чем с другой стороны, причем наступит такое положение, при к-ром суммы моментов сил тяжести относительно оси вращения справа и слева окажутся равными по величине, после чего колесо остановится. Видоизменением указанного проекта является проект механизма,указанного на фигуре 2. В закрытом барабане с изогнутыми перегородками находятся тяжелые шарики, которые, перекатываясь во время движения барабана, то находятся у внутренних сторон стенок барабана то концентрируются в центральной его части, обеспечивая этим якобы непрерывное вращение барабана. Невозможность постоянного вращения барабана без сообщения внешней энергии очевидна из рас-суждений, аналогичных предыдущим. Аналогичный принцип лежит и в основе проекта механизма, изображенного на фигуре 3. На законе Архимеда основан например следующий пр оект осуществления Р. т.

Имеется ряд полых шаров,нанизанных на нить; часть из них находится в жидкости, другая часть — в воздухе (фигура 4). Идея этого механизма заключается в том, что полые шары должны последовательно всплывать на поверхность жидкости, увлекая за собой и всю цепь нанизанных шаров, попадающих попеременно из воздуха в жидкость и наоборот. В свою очередь шары могут приводить в движение вертушку, и Р. т. как будто бы

осуществлено. Невозможность осуществления этой идеи,не говоря о трудностях устройства входного отверстия, или сальника, заключается в том, что шар, входящий в жидкость, не только не всасывается последней снизу вверх, но встречает, наоборот, противодействие состороны жидкости к своему проникновению в нее, причем работа, затраченная на то, чтобы протолкнуть шар в жидкость, не меньше той работы, к-рую шар возвращает при своем всплывании на поверхность. Так. обр. выигрыша энергии не будет, и механизм в вечном движении быть не может. На принципе магнитного притяжения основывается следующая схема осуществления Р. т. На верхнем конце наклонной плоскости АВ (фигура 5) находится магнит М, притягивающий к себе металлич. шарик, перемещающийся по плоскости АВ. На пути к М шарик встречает отверстие О, в к-рое он и проваливается, попадая затем на изогнутую поверхность CDE, имеющую закругление в нижнем своем конце. В своем обратном движении шарик, вследствие закругления D, окажется в нек-рый момент над плоскостью АВ и снова начнет свое движение по последней, снова провалится в отверстие О и т. д. Нетрудно усмотреть однако, что в действительности произойдет одно из двух: или шарик проскочит мимо отверстия и притянется магнитом или же в каком-нибудь положении на поверхности он остановится благодаря тому, что сила притяжения, сила реакции поверхности и вес шарика взаимно уравновешиваются в этом положении.

Помимо вышеуказанного Р. т., носящего название perpetuum mobile 1-го рода, рассматривают еще и т. и. perpetuum mobile 2-го рода, сущность которого заключается в следующем. Как известно из термодинамики (смотрите), можно произвольное количество тепловой энергии преобразовать в любой другой вид энергии в соответствующем строго определенном количестве. Однако же такое преобразование тепловой энергии возможно лишь при наличии носителей различных темп-p и отдачи определенного количества тепла носителю с низшей темп-рой (2-й закон термодинамики). Механизм, при помощи которого можно было бы превратить тепловую энергию какого-нибудь тела в другой вид энергии, в частности в механич. работу, без наличия перепада темп-p между данным телом и другим каким-либо носителем тепла и притом без всякого изменения термин, состояния окружающей среды, и осуществил бы Р. т. 2-го рода. Несмотря на тЬ, что тепловая энергия, находящаяся в любом теле, вполне ограничена и что вследствие этого даже при осуществлении Р. т. 2-го рода едва ли можно было бы говорить о вечном движении,—все же этот термин имеет некоторое оправдание в том, что преодоление сил трения и других вредных сопротивлений механизма должно обратно переводить определенное количество механич. энергии в тепловую энергию.

Лит.: Planck М., Das Prlnzip der Erhaltung d.Energie, Lpz., 1908; Schafer C., Die Prinzipe der Dynamik, B., 1919. M. Серебренников.