 > Техника, страница 12 > Аналитическая геометрия
> Техника, страница 12 > Аналитическая геометрия
Аналитическая геометрия
Аналитическая геометрия, отрасль математики, занимающаяся геометрическими исследованиями при помощи методов алгебры и анализа. А. г. основана па определении положения точек в пространстве при помощи чисел, называемых координатами. На плоскости выбирают неподвижную точку О и две пересекающиеся прямые ОХ и OY (координатные оси) (фигура 1). Положение любой точки Р на п л о-с кости определится, если разложить отрезок ОР на два составляющих отрезка OQ и QP, параллельных координатным осям, или OR и RP. Число х, выражающее длину отрезка OQ, называется абсциссой точки Р, а число у, выражающее длину отрезка QP, называется ординатой той же точки. Числа х и у считаются положительными, если отрезки OQ и QP направлены в те лее стороны, что и соответствующие оси ОХ и OY, и отрицательными, если они обращены соответственно в противоположную сторону. При этих соглашениях каждой точке на плоскости отвечают вполне определенные значения абсциссы ж и ординаты у и обратно, каждой паре значений х и у отвечает одна точка на плоскости. Абсциссы и ординаты носят общее название координат точки Р.
Обычно угол между координатными осями берется прямой, тогда составляющие 0Q и QP вектора ОР являются его прямоугольными проекциями (ортогональные координаты). Этот способ координации (определения положения точки) был указан Декартом (1637 г.), и поэтому самые координаты носят название декартовых.
Можно определять положение точки Р на плоскости также и при помощи полярных координат, указывая длину отрезка ОР=г и угол Θ между осью ОХ и вектором ОР.
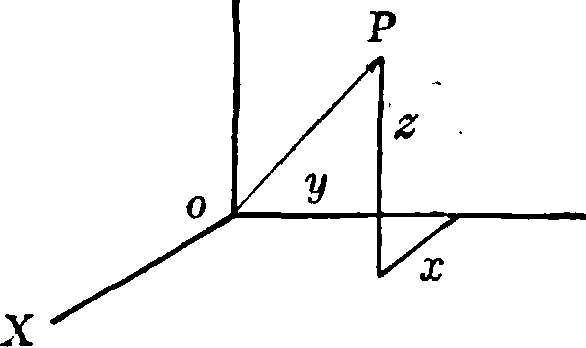
Фигура 2.
Положение точки Р в пространстве определяется при помощи трех чисел. Через точку О проводят три непараллельных одной плоскости прямых ΟΧ, ΟΥ, 0Z и разлагают ОР на составляющие, параллельные этим прямым (фигура 2). Здесь каждой координате также присваивается знак в зависимости от того, совпадает ли составляющий отрезок с направлением соответствующей координатной оси или же имеет противоположное направление. Положительные или отрицательные числа, равные этим составляющим, обозначаются обыкновенно буквами х, у, z и называются коор-2 динатами точки
Р в пространстве. Чаще всего берут три взаимно перпен-чг дикулярные оси ъ OX, OY и OZ. Тогда составляющие радиуса-вектора ОР становятся равными прямоугольным проекциям его на координатные оси, а соответствующие числа х, у, z называются прямоугольными координатами точки Р или радиуса-вектора ОР.
Положение точки Р в пространстве м. б. определено и другими координатами. Можно, например, построить сферу с центром в О, проходящую через точку Р, и выбрать на этой сфере экватор и начальный меридиан. Тогда сферическими координатами точки Р называют три числа: радиус сферы, широту и долготу точки Р. Число координат, необходимых для полного определения положения точки Р, равно числу измерений рассматриваемого пространства. Для исследования геометрич. свойств различных фигур в пространстве и их взаимного расположения надо выразить эти свойства при помощи ур-ий, связывающих между собой координаты точек, принадлежащих этим фигурам. Например координаты всех точек сферы с центром в О удовлетворяют ур-ию а2 + у2 + z3=R2 (где R — радиус сферы), ибо квадрат радиуса-вектора равен сумме квадратов его проекций. В общем виде ур-ие f{x, y,z)=0 выражает нек-рую п о-верхность. На плоскости можно предположить z=0; тогда ур-ие fix, у)=0 выражает нек-рую линию, т. к. это ур-ие м. б. решено относительно одной из координат: у=у(ж), причем каждому значению х соответствует одно или несколько значений у, а следовательно,—определенные точки на плоскости. Обратно, каждая кривая может быть выражена ур-ием между координатами ее точек.
Целый ряд геометрич. задач м. б. разрешен при помощи алгебраич. вычислений. Напр., если даны две кривые в ур-иях
fix, у)=0 и F{x, у)=0,
то для нахождения точек пересечения этих кривых достаточно решить совместно эти два уравнения. Полученные значения координат х и у будут координатами точек пересечения. Во многих задачах целесообразно не определять радиусы-векторы различных точек при помощи координат, а вести вычисления непосредственно над радиусами-векторами этих точек при помощи методов векторной алгебры. Этот метод имеет большие преимущества для исследования линейных фигур, прямых линий, плоскостей и их взаимного расположения.
Методы А. г. имеют громадное значение для разрешения задач механики и физики.
Лит.·. М л о д з e е в с к и и Б. К., Основы аналитич. геом. на плоскости, ГИЗ, 1923; его же, Основы аналитпч. геом. в пространстве, М., 1924; Соколовский И. И., Аналитич. геометрия в векторном изложении, Москва, 1926; Поляков А. П., Аналитич. геом., 1926; Цубербиллер О. Н., Сборник задач и упражнений по аналитич. геом., ГИЗ, М., 1 927. Я. Шпнльрейн.