> Техника, страница 15 > Арки

Арки

Арки, арочные фермы. В строительном искусстве и в строительной механике А. называются конструкции с таким устройством опор, при котором при вертикальной нагрузке получаются ие только вертикальные, но и горизонтальные составляющие опорных давлений, или так называемым горизонтальн. распор. Арочные конструкции

исполняются из камня, бетона, железобетона, металла и дерева. По конструкции различают А. сквозные и А. со сплошной стенкой. По устройству опор А. делятся на 1) трехшарнирные, 2) двухшарнирные и 3) бесшарнир-н ы е, или А. с защемленными пятами. А., имеющая три шарнира — два в пятах и один в ключе,— статически определима; она нечувствительна к изменениям t° и небольшим осадкам опор. Двухшарнирная А. статически неопределима в первой степени. Бесшарнирная А. статически неопределима в третьей степени.

А. с одним шарниром — система с двукратной статической неопределимостью — применяется в практике, но пока сравнительно редко. Во всех последних А. от колебаний t° по сравнению с начальной, при которой А. была устроена, и от смещений (осадок) опор возникают дополнительные напряжения. На фигуре 1 У,

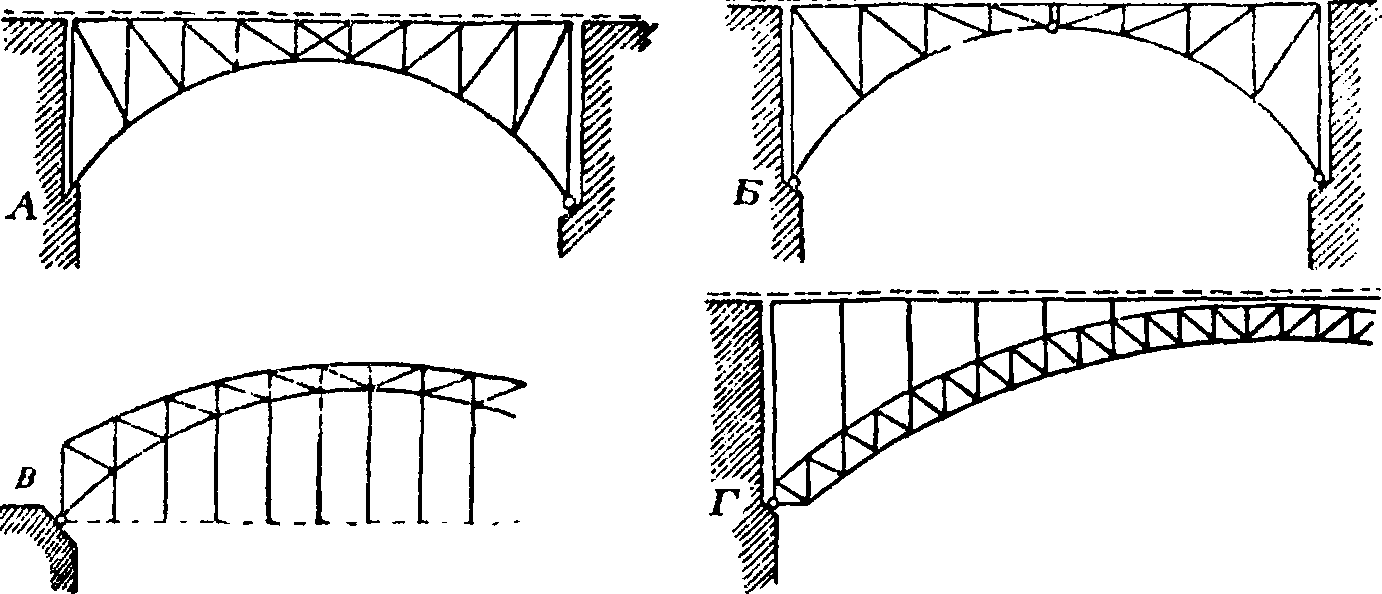
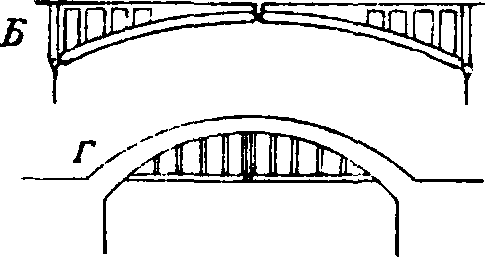
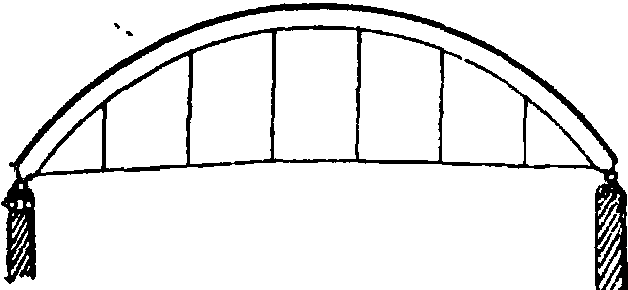
{А, Б, В, Г и Д) даны приме- Д ры арочных сквозных ферм (мо стовых). В настоящее время в Сиднее (Австралия) строится арочный сквозной мост пролетом ок. 500 ж, пока наибольший в мире. А. со сплошной стенкой в применении к мостовым фермам показаны на фигуре 2 (А, Б, В и Г). Двухшарнирная А. со сплошной стенкой употребляется гл, обр. для железных мостовых ферм, в железобетонных сооружениях и в сводах. Трехшарнирные и бесшарнириыо А. нашли большое в~Ш^

Фигура 2. Примеры сплошных мостовых арочных ферм: А — двухшарнирная сплошная арка, Б — трехшарнирная сплошная арка, в — бесшарнирная сплошная арка, Г—железобетонная арка с подвешенным мостовым полотном. распространение в сводах из камня, бетона и железобетона и менее употребительны в железных конструкциях. Объясняется это малой жесткостью железных трехшарнирных А., получающихся очень легкими, а также — трудностью осуществления безупречной заделки бесшарнирных железных А. в каменных опорах. Устройством шарниров в пятах А. достигается передача опорных давлений в определенных точках (смотрите Опоры), что дает возможность достигнуть более выгодных распределений н а-пряжений в опорных частях сооружения. Кроме того, введение шарниров понижает влияние температурных изменений и осадок опор; так, при одинаковом изменении t° в обычной плоской бесшарнирной А.

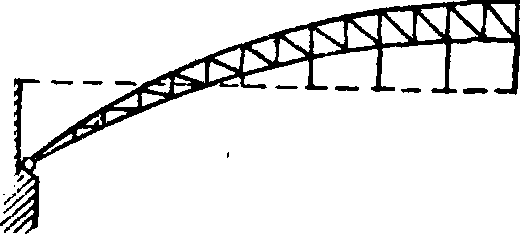
распор в несколько раз больше, чем в такой же А. с шарнирами в пятах. Распор А. иногда нельзя передать на опоры, которые пришлось бы строить слишком сильными. Невыгодно, например, перекрывая А. высокое помещение, передать распор на высокие стены. В таких случаях оба шарнира соеди

Фиг.

3. Стропильная арка с затяжкой.

Фигура 1. Примеры мостовых сквозных арочных ферм: А—двухшарнирная арка с ездой по верху, Б — трехшарнирная арка с ездой по верху. В—двухшарнирная арка с подвесным мостовым полотном, Г—двухшарнирная арка с ездою по верху, Д—серповидная двухшарпирная арка с ездою по середине. няются затяжкой, а один из них делается подвижным (фигура 3). Затяжка, устраиваемая горизонтальной или с небольшим подъемом, воспринимает полностью горизонтальный распор. Благодаря упругому растяжению затяжки распор получается несколько меньше, чем при полной неподвижности опорных шарниров.

В статическом отношении к А. принадлежат рамы (смотрите), очень употребительные в железобетонных сооружениях (фигура 4 А. и Б). Рамы имеют такое же устройство опор, как А., но очертание их, в отличие от А., делается не по линии давления или по какому-либо другому постоянному закону, а представляет обычно многоугольник очертания, соответствующего назначению перекрываемого помещения. Рамные констру-

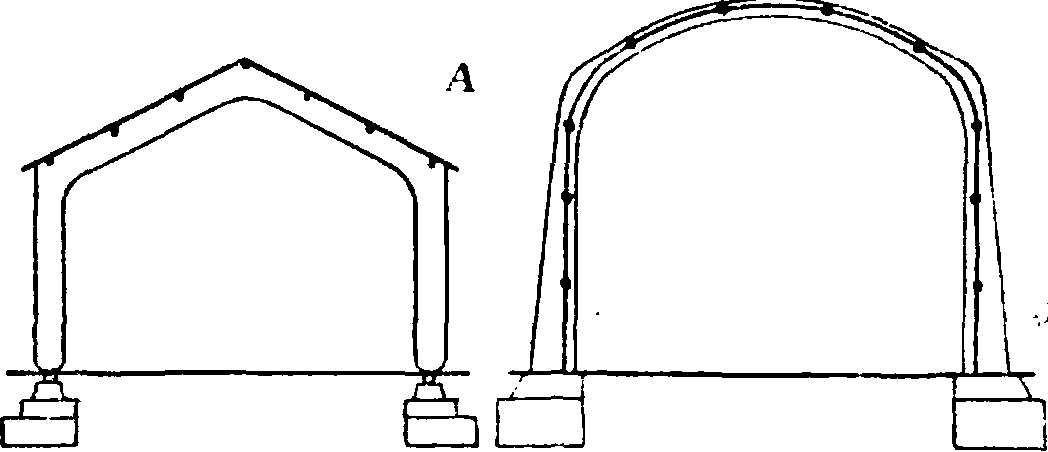
Фигура 4. Примеры рамных конструкций: А—ординарные рамные перекрытия, В—сплошные рампые перекрытия. кции применяются для перекрытия больших помещений (зал, фабричн. корпусов и т. д.). Рамы применяют с защемленными или

шарнирными пятами; третий, промежуточный, шарнир встречается сравнит, редко в рамных конструкциях. Арки неразрезные, со сплошной стенкой, перекрывают несколько Пролетов. Неразрезные А. в пятах между собой связаны и имеют общие опорные части, так что от нагрузки в одном пролете возникают напряжения и в остальных.

Если не считать нескольких обособленных неэкономичных, разобранных в литературе, примеров, — применимость А. неразрезных ограничивается только тем случаем, когда промежуточные опоры настолько высоки и гибки, что не могут осуществить полной неподвижности пят бесшарнирных А. и в особенности сводов. От нагрузки одного из двух примыкающих к опоре сводов опора изгибается и тем самым вызывает дополнит, напряжения в смежном пролете (подробнее см. Своды, расчет).

А. простые со сплошной стенкой.

Простыми называются А., перекрывающие один пролет. В статическом отношении различают трех-, двухшарнирные и бесшар-нирные А. Ось А. большей частью бывает очерчена по линии давления от постоянной или полной нагрузки. Поэтому чаще других встречаются А. параболические.

I. Трехшарнирные А. Эти А. статически определимы относительно опорных · реакций. В общем случае, при любом направлении нагрузки, вертикальные слагающие опорных реакций определяются как в про

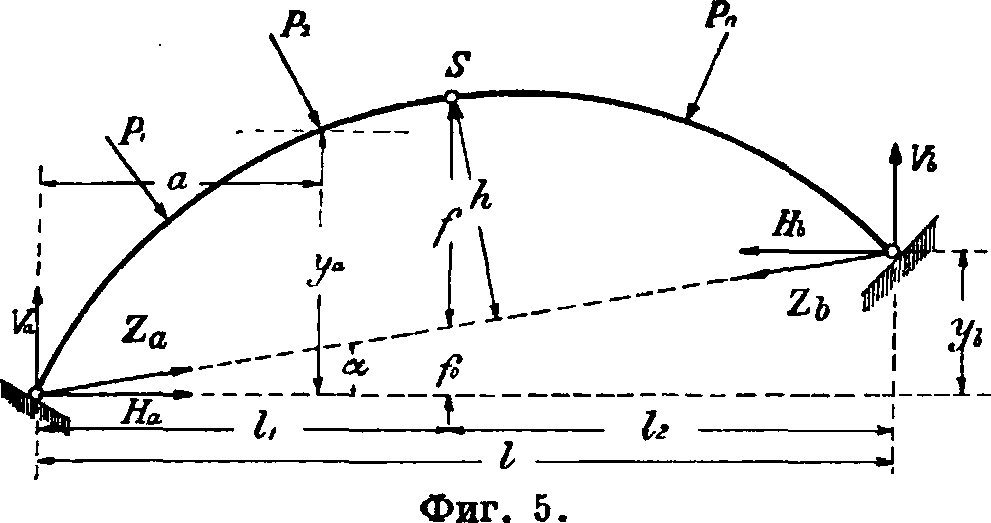
стой балке, из условия равновесия относительно шарнира другой опоры (фигура 5):

⁷«⁼⁼т[2!^Рсо8<^р»^г)(^г-^а)— 2!^{р sin} г) (у«—Уь)];

^Fb=T[2l^Pcos(^p’^^a-

-2!^Ρ8ίη {Р,Т)Уа ·

Слагающая по линии пятовых шарниров определяется из уравнения проекций на горизонтальную ось:

Z_a cos а — Z_b cos а + У! Psin(P, У)=0,

или Н_а-Н_ъ — 2;Psin(P,r)=0.

Величина слагающей H_a=Z_a cos а определяется из ур-ия момента относительно ключевого шарнира:

ТТ Г, Mg Mg

ri_a — Z_a COS a=-т-s COS a=~ · h f

При действии на А. только вертикально направленной нагрузки вертикальные слагающие опорных реакций точно равны опорным реакциям простой балки: V_a=Aq и V_b=В_оги слагающая распора H_a=H_b=M_g: f. Момент в любом сечении трехшарнирной А.

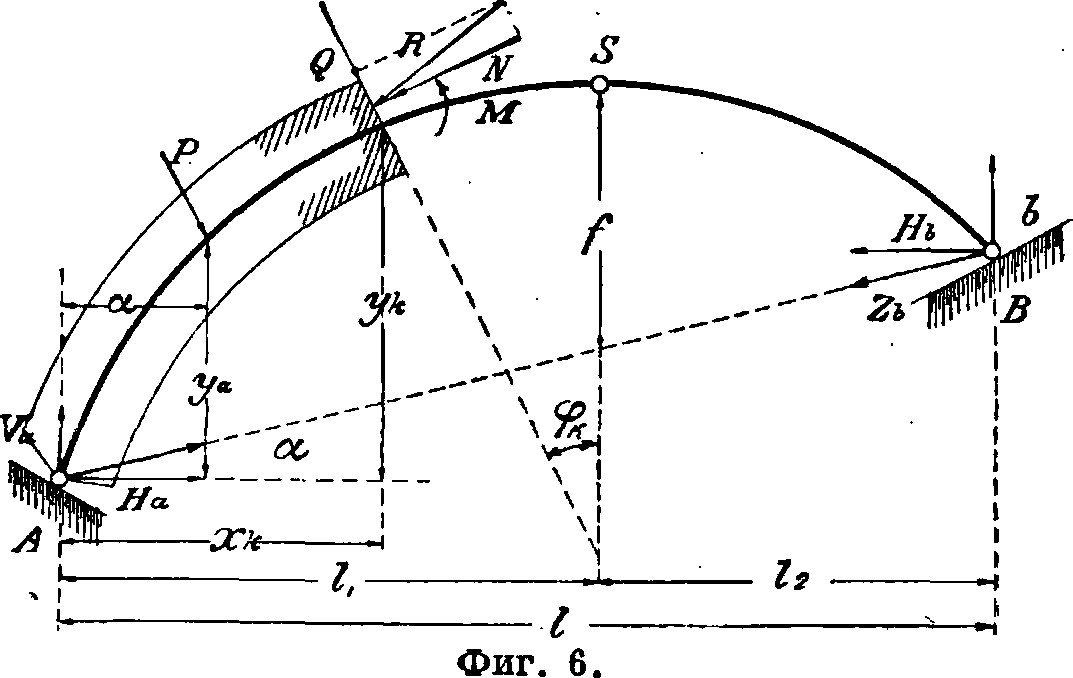
определяется уравнением (фигура 6): М_Х=М₀— —А (у_к—х_к tg «), где М₀—момент относительно сечения всех внешних сил, слева от него лежащих. Нормальная сила в том же сечении: N_X=N₀+H (cos y+tg« sin у), где N₀—проекция в сечении на ось А. всех внешних сил, слева от сечения лежащих, в том числе и опорной реакции. Поперечная сила в сечении: Q_x=Q₀ — Н{sin у — tgacosy), где Q₀—проекция на ось, перпендикулярную к оси балки, всех сил, слева от сечения лежащих. При расположении пят А. на одном уровне: М_х=М₀ — Н_у; N_x==Qo sin у + Η cos у; Q_x=Q₀ cos у — H sin у.

JR

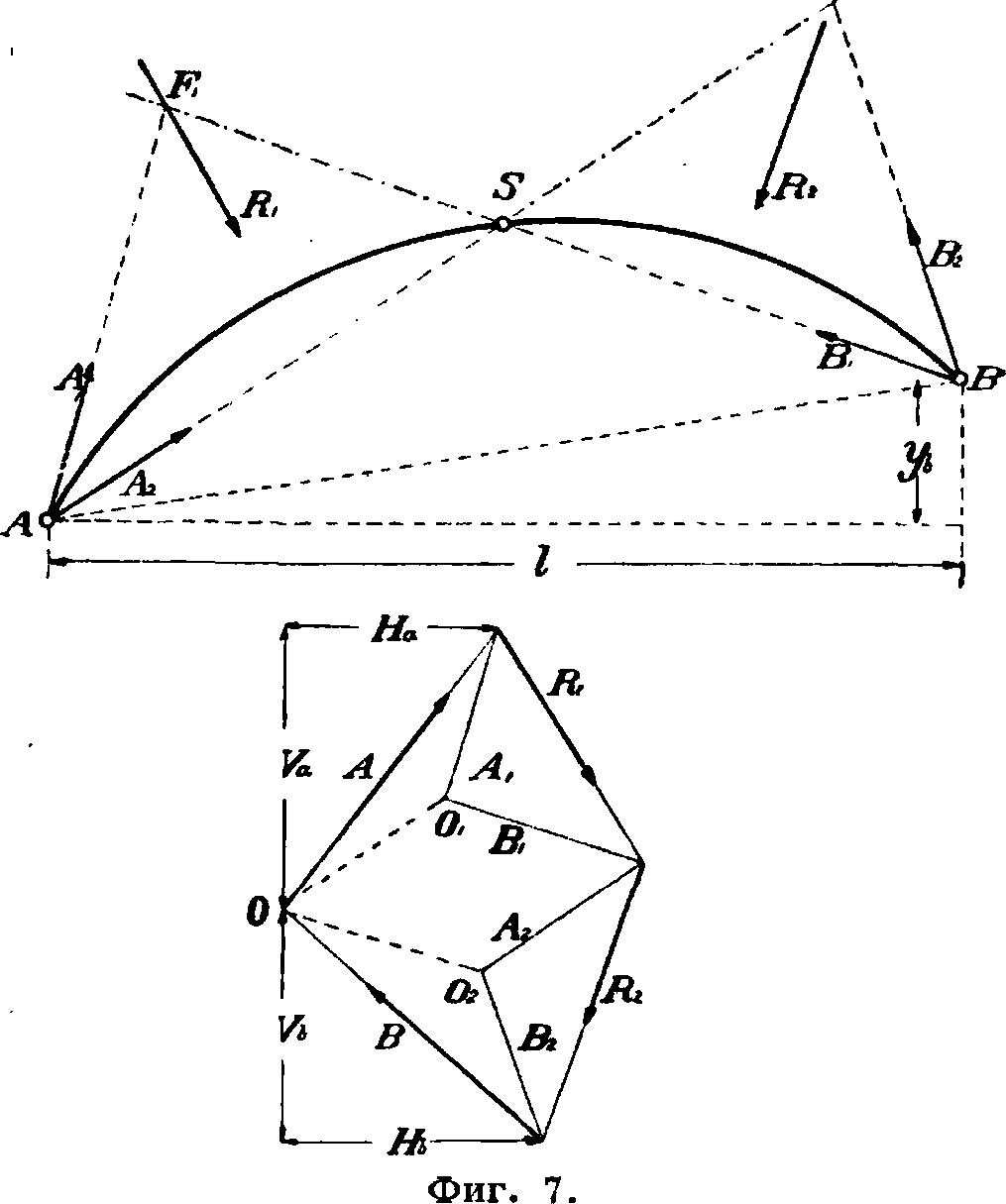
Если А. находится под действием неподвижной нагрузки (снег, собственный вес и т. д.), то опорные реакции, внутренние силы и моменты легко определяются построением многоугольника давлений, проходящего через три шарнира А. Способ построения показан на фигуре 7. Посредством вспомогательного мн-ка с полюсами О_г и 0₂ находят равнодействующие В_л и В_2>приложенные в левой и правой частях А.

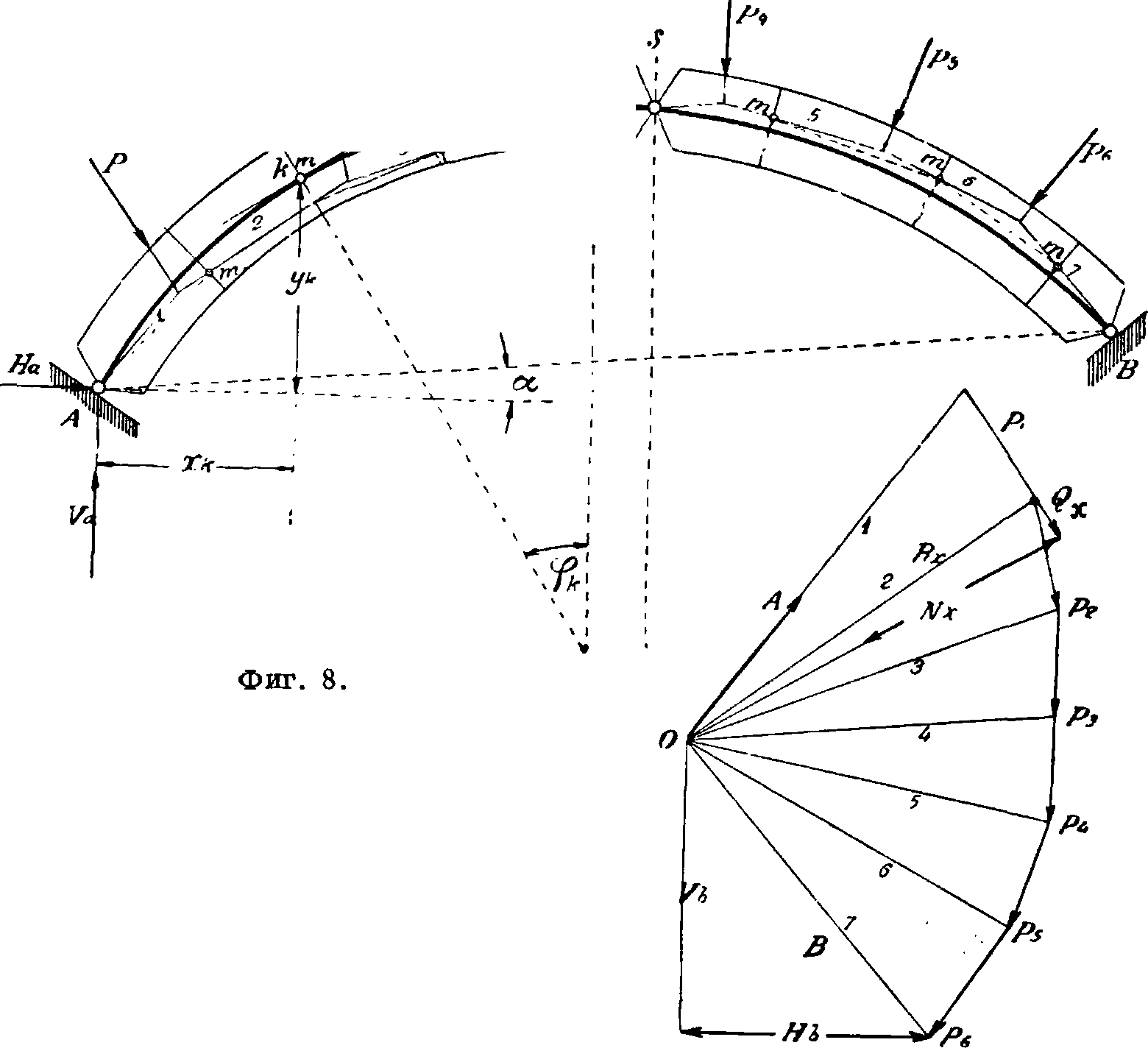
Каждую из сил R_x и R₂ разлагают на составляющей е А_г, В_х и А₂, В₂. Силы А_х и А₂, В_х и В₂ дают равнодействующие А и В опорных сопротивлений, которые разлагаются на вертикальные составляющие V_a и F& и горизонтальные Н_а и Н_ъ. Точка О в пересечении сил Аж В является полюсом искомого силового мн-ка (линия ОО_х II А/Sи 00₂II SB). Полученный силовой мн-к каждым своим лучом «определяет направление равнодействующей R_xвсех сил, слева от нее лежащих (фигура 8). Разлагая R_x на направление нормали к сечению и на направление касательной к оси в сечении, получают величину нормальной силы N_x и поперечной силы Q_x в сечении А. Величина момента в сечении A.: M_x=R_xr=

=N_xri, где г — плечо равнодействующей R_x, а -η— расстояние точки приложения давления в сечении от центра сечения.

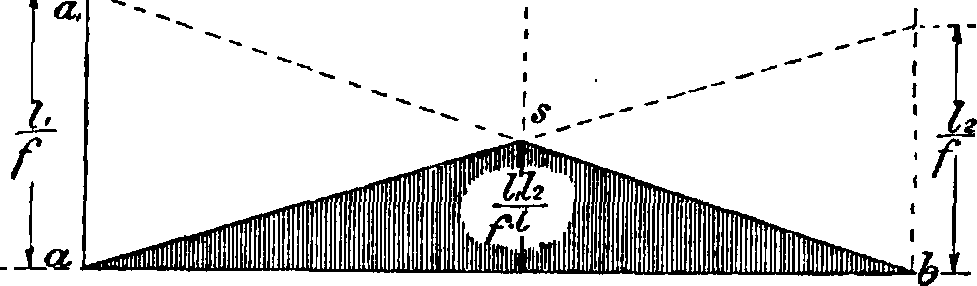
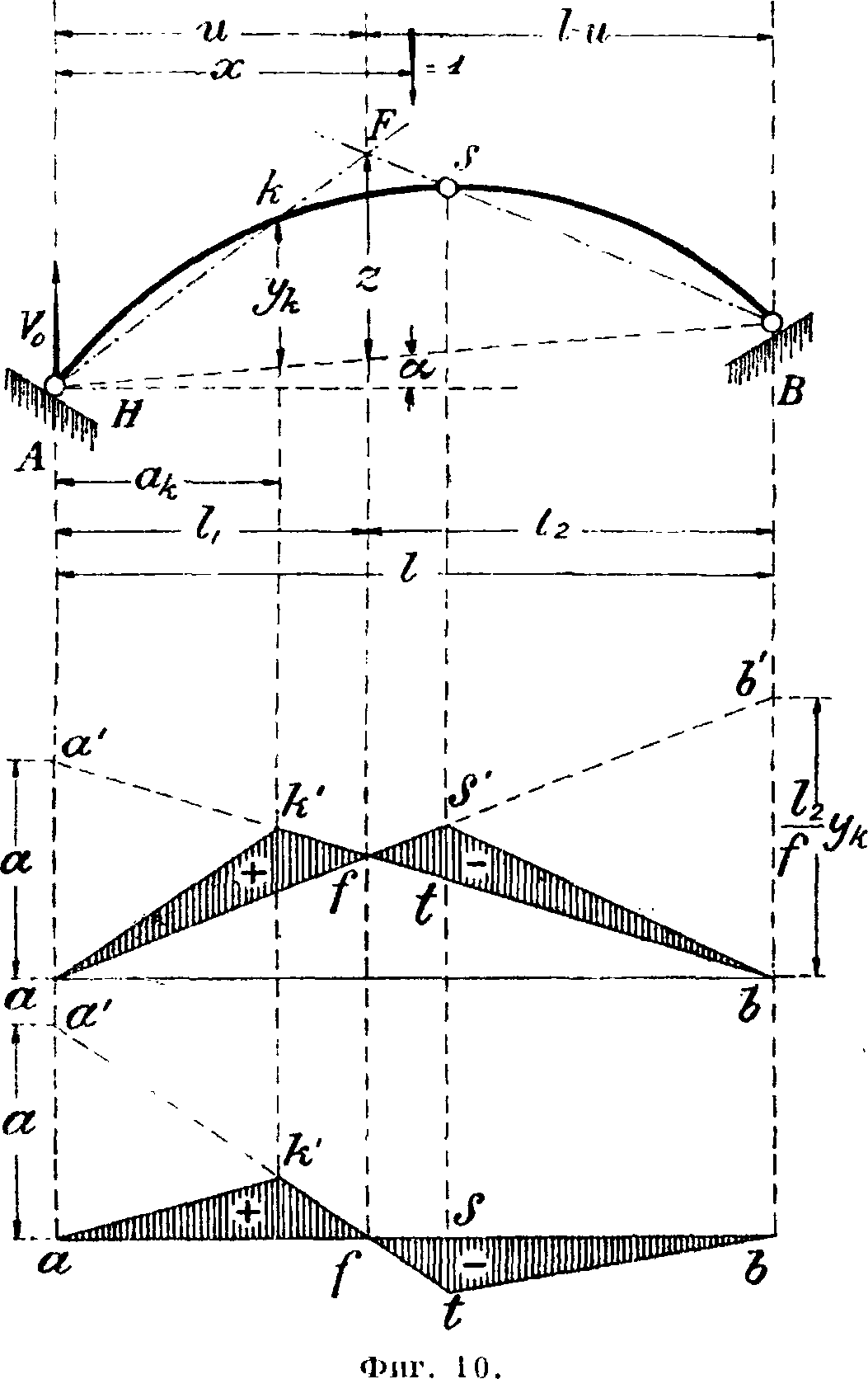
При загружении А. подвижной нагрузкой строятся линии влияния, для чего А. загружается одним вертикальным грузомР=1. Линии влияния Уд и V_b строятся так же, как в двухопорной балке (фигура 9). Линия влияния распора Н определяется из ур-ия H—Mg : f и поэтому строится как линия влияния момента двухопорной балки в сечении под шарниром с изменением ее ординат в отношении 1 : /Хфигура 9). Линия влияния момента в сечениях А. определяется ур-ием <фигура 10): М_х=М₀—Н(у—а_к tg *), то есть ординаты ее получаются как разность ординат линии влияния М₀ момента двухопорной влияния М₀ равна ординате линии влияния Н{у_к—а_к tg а). Эта точка F определяется пересечением проводимых в А. прямых BS—через шарниры В и S и прямой Ак— через шарнир А и точку к момента в сечении А. (фигура 10). Груз=1, ставший в точку F, разлагается по направлению опорных

	Рз
		т 4 f

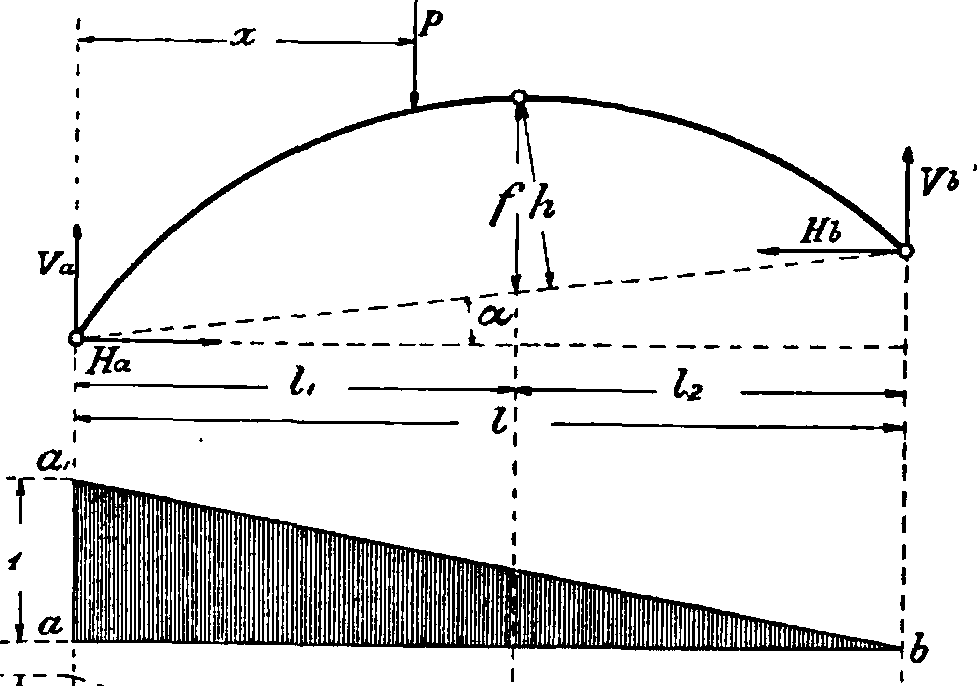
реакций BS и Ак но т. к. реакция Ак проходит через точку к, то, следовательно, момент относительно нее=0; определив точку F, проводят вертикаль до оси абсцисс линии влияния (точка f), откладывают на левой опоре отрезок а_к, равный расстоянию до рассматриваемого сечения, и проводят прямую af на эту прямую сносят положение моментной точки к и положение ключевого шарнира S; контуром aktb очерчивается линия влияния момента. Она получается разных знаков; число изменений знака зависит от положения точки раздела F. Если точка F попадет в правую часть А., то нулевая точка f становится фиктивной, и линия влияния имеет один знак.

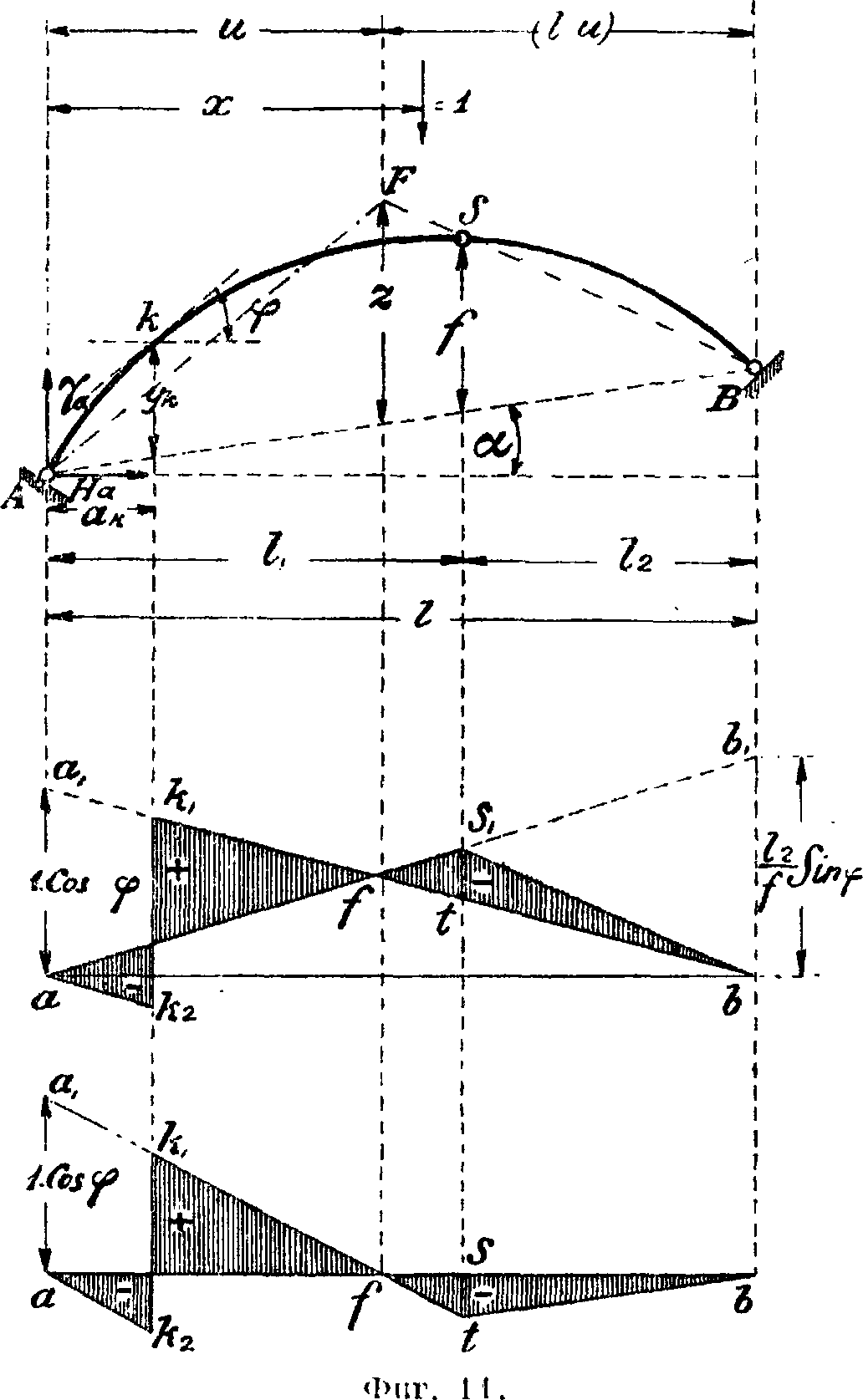
Линию влияния поперечной силы находим из ур-ия: Q= Q₀cos у—iT(siny—tg α cos у), т. e. она определяется разностью ординат линии влияния поперечной силы Q₀ двухопорной балки, умноженных на cosy, и ординат линии влияния распора, умноженных

Фигура 9.

балки и ординат линии влияния Н распора, измененных помножением на у — %tga. Построение линии влияния упрощается, «если найти точку раздела F, т.е. того положения груза=1, при к-ром М_х=0. На .вертикали под этой точкой ордината линии на sin у — tg*cos у; при a=0, @=()₀cosy — — i/siny (фигура 11). Построение линии влияния м. б. упрощено определением точки раздела F, при положении в которой груза=1 поперечная сила Q_x=0. Эту точку F находят проведением в А. прямой BS и прямой AF из левого шарнира параллельно касательной к оси А. в рассматриваемом сечении (фигура 11). Положение точки F сносят на ось абсцисс линии влияния, откладывают на вертикали под левым шарниром ординату aa_x=l.cosy и проводят прямую aj, на которую сносят точку к центра оси сечения и точку S ключевого

шарнира; контуром ak^k-fb очерчивается линия влияния поперечной силы. Если грузо-раздел F окажется слева от шарнира S,

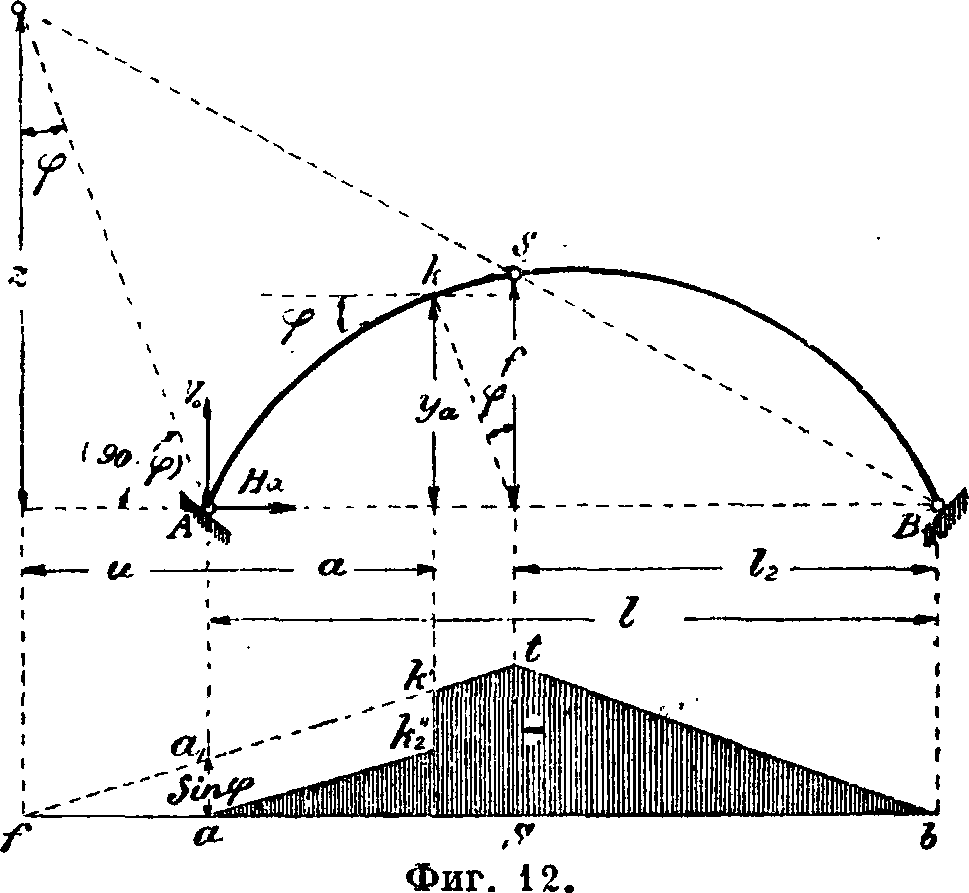
то .чинил влияния Q дважды меняет свой знак; если она ляжет справа от шарнира S, то нулевая точка f является фиктивной, и линия влияния меняет знак один раз. Аналогичным приемом строится (фигура 12) линия влияния N по ур-ию N_x— Q sin ψ +И (cos ψ j-h tg « sin y).

Напряжения в сечениях А. определяются по условию неравномерного сжатия:

N. М. -

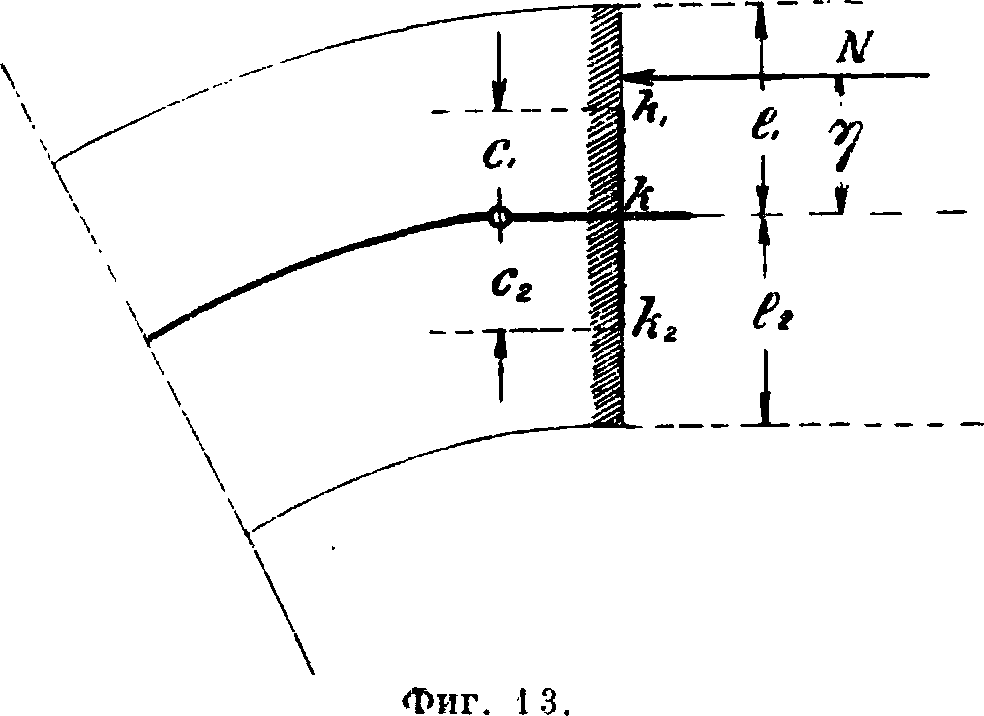
п—~^ + ~ге, где е — расстояние до крайней точки сечения. При загружении А. подвижной нагрузкой вычисление затрудняется отысканием наибольшего значения N и М по двум линиям влияния. Это затруднение устраняется расчетом по «ядровым моментам» (фигура 13), то есть заменой точки моментов относительно оси свода точками моментов относительно крайних точек к_г и /л, ядра сечения:

N.Μ N, „.. N,. _ч М"

*=F⁺T^e

N

F

М

_те-

I

N

(/»²+>3^)=

[ (e₂+y>)Ci~ _f

N Μ

(ρ² —4C₂)=J (Cl -ч)е_а=-ре.

Моменты M и М", соответствующие крайним точкам ядра сечения, определяются так же, как момент М_х относительно осевой точки к,— по соответствующим им координатам. Построение линий влияния для них аналогично построению линии влияния для М_х, с той разницей, что вместо коорди нат осевой точки к берутся координаты ядровых точек к_л и к_г.

Рациональная ось А. Рациональной осью А. будет та ось, которая совпадает с кривой давления. При загружении А. сплошной, равномерно распределенной

но горизонтальной линии, нагрузкой интенсивностью д кг1п.м., кривая давлений очер-

f

тится по параболе с ур-ием у — х (I — х),

7 7 * ^ίχί*

в к-ром 1_г и 1_г— расстояния от промежуточного шарнира до опор А. При загружении

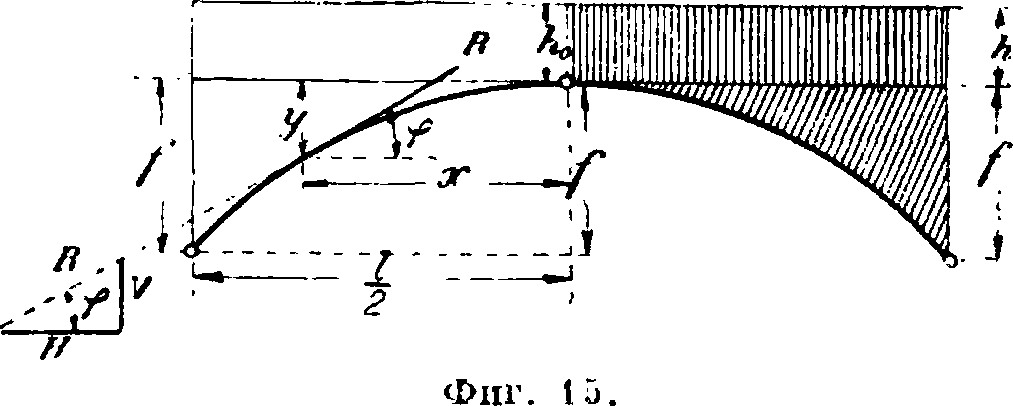
F

А.сплошн. нагрузкой по оси ее, ось А. очертится по кругу. При сплошном надсводном строении нагрузка будет меняться (фигура 15) от до 1ц+/‘, поэтому для определения

4 ίΊ

с уравнением у — х{1 —х).

та у

Ордина-

этой параболы в точке на расстоянии

четверти пролета от опор равна */4 Л тангенс угла наклона касательной к оси в том же

2 f

сечении у —

I

ее необходимо предварительно знать ось А. Предварительное определение формы кривой оси А. можно сделать или по формуле Legay:

х у — 1ц cos h

где

f

VHfy

h

arc cos h

а у — вес м⁸ надарочного заполнения, или по упрощенной ф-ле

8 /ж² (31цР + 2 /ж²)

~~>(0|» + /Г

Построенные по этим ординатам кривые дают первое приближение для оси свода; построив эту ось, вычисляют для нее действительную нагрузку, строят но ней веревочную кривую, проходящую через три шарнира, и принимают эту кривую за ось свода. При наличии подвижной нагрузки кривая давлений изменяет свое очертание в зависимости от положения нагрузки на А.; поэтому при выборе оси А. задаются загружением каждой части А. от пятовых шарниров до промежуточного, находят положение кривых давлений для обоих случаев загружения (фигура 14) и намечают ось А.

Н а г р у з к а	Вертик. оиорн. реакц.	Распор	Моменты в четвертях арки	Норм, силы в четвертях арки
Один груз в ключе арки	р А=В=~г-1	Р1 н— 4	Р1 16	до·.!·.
Один груз в правой четверти пролета	3 Р h,- 4- « Г		3 Р1 ^ 32 Р1 32	Р 12/*-Иа 8/ |/4Л+1*
Равном.распределенная нагрузка по всему пролету		qp Н=—— 8	0
Равном.распределенная нагрузка в левой половине арки	‘-Ψ	л~^ 16	_£L 64, 9I-т 6 4	тУ^+1Ж

Фигура i 4.

так, чтобы отклонения обеих кривых давлений от оси А. были наименьшими. Ниже приведены ф-лы для расчета трехшарнирной симметричной параболической

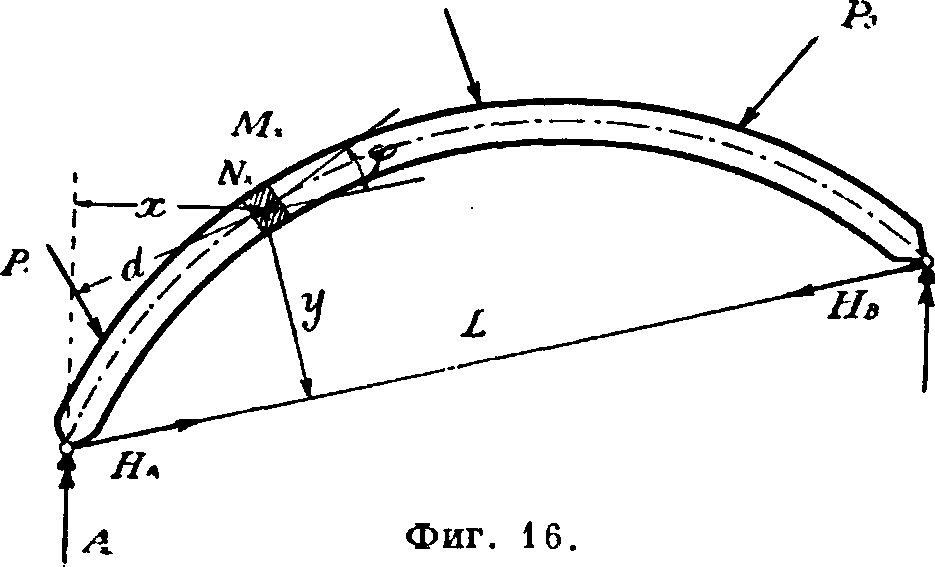
II. Двухшарнирные А. имеют одну статически неопределимую величину, т. к. для нахождения четырех неизвестных опорных реакций (по две на каждой опоре) имеем только три уравнения статики. Опорные реакции, возникающие от некоторой произвольной нагрузки, показаны на фигуре 16. Они разложены на вертикальные составляющие и составляющие по линии, соединяющей оба опорных шарнира. Вертикальные составляющие каждой из опор определятся, если взять момент всех внешних сил, приложенных к А., относительно другого опорного шарнира,—так же, как это делается в простых двухопорных балках:

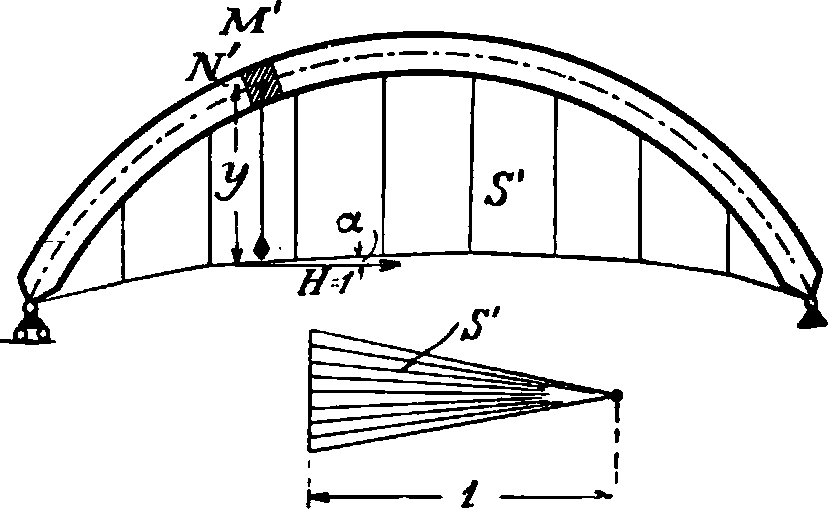
А=у я В — у 2 где а и b—плечи грузов Р относительно пятовых шарниров А. Ур-ие для определения неизвестного распора На напишется из условия, что длина L пролета не изменяется при деформации под влиянием сил N_x и изгибающих моментов М_х; влиянием поперечных сил пренебрегаем. Выделим элемент (клин) длиной ds с координатами ж, у. Если представить этот элемент упругим, а лежащие справа и слева от него части А. совершенно жесткими, то эти части повернутся от нагрузки одна от носительно другой на угол сблизятся на величину dds =

EF

и

Длина L изменится поэтому на величину N

dl=d<?.y— y—rds.cosy. Допустим, в общем М/М *

случае, что опоры не неподвижны, а получают от нагрузки определенное, хотя и

малое, смещение dL. Учитывая при этом температурное удлинение, можем написать:

dL=f^fy^ds—f ds.cos ψ ±atL,

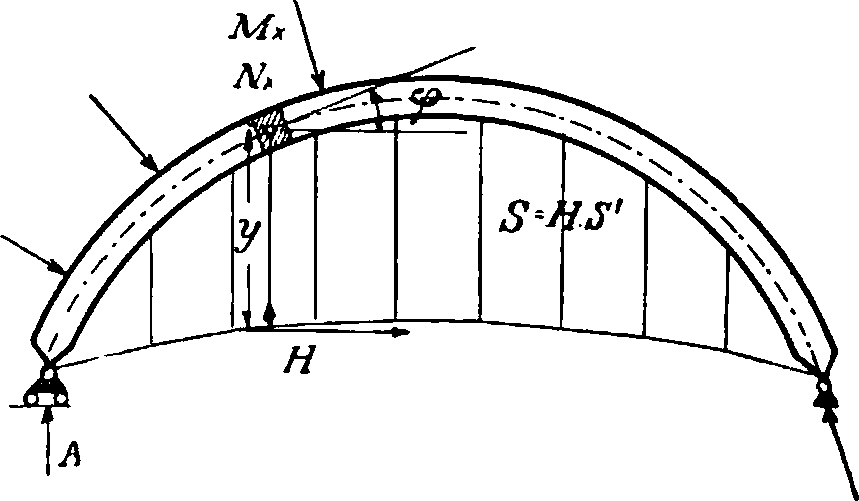
где « — коэфф. температурного удлинения. Т. к. момент в любом сечении арки М_Х=М₀ — —Н_Ау и нормальная сила Ν_Χ=Η_Λ cos ψ+Ν₀,

то, подставив эти величины в выражение dL, после приведения получаем формулу для распора:

r*jV„ ds.COS φ

Η_Α =--

— EbL+f^fvda — f-1

± EatL

*ds F

(1)

ъг ^cos <P

В этом выражении M₀ — момент в сечении А. как простой балки, N₀ — проекция на ось А. всех сил, слева от сечения лежащих. Из этого общего выражения можно определить Н при любом очертании А. При переменных и/’интегрирование надо заменить суммированием, разбив А. на большое число конечных элементов (клиньев) ds, и вычислить подинтегральные выражения для середины каждого элемента. В рамах, где линия давления сильно отклоняется от оси, пренебрегают влиянием нормальной силы N_x на деформации. Тогда в выражении Н отпадают члены, содержащие F (смотрите Рамы). В пологих двухшарнирных А., с одной вертикальной нагрузкой, Н_А=Н_В =Н в таких

А. с достаточной степенью точности можно принять cos ψ=1 и пренебречь величиной проекций вертикальных сил на ось А. <А₀=0). В этом случае выражение Н напишется так:

-Edl+/—¹f— ± ЕМ

Ίψ+Τψ

(2)

При учете влияния одной вертикальной нагрузки (dl=0 и ί=0) выражение Н приведется к виду:

Н

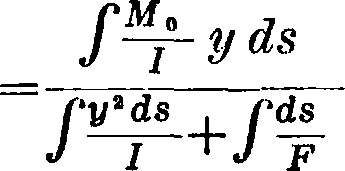
(3)

Если ось А. очерчена по закономерной кривой (например по параболе или по кругу) и сечение ее постоянно, то входящие в выражение распора интегралы могут быть вычислены аналитически.

Двухшарнирная параболическая симметричная арка

(фигура17).Ур-иеоси такой А .:у=-^х(1 — х),

где f—подъем А. в ключе. Приняв средние значения Icosf—c и Fcos<p=k за постоянные, мы можем каждый из интегралов вы

ражения (3) представить в таком виде:

Подставляя вместо М₀ значение момента в сечениях слева от груза Р: М₀~Р ^ ~ ^а х, и

Ра в сечениях справа от груза Р: {1—х),

получим:

— f Mdy dx= —f ^ Ху(- х (I — х) dx 4-

С ** С * q I 1^л

+ ~f -f{l — x)%x(l—x)dx=

1 f

= — Pati — a)(l^z-{-la— α²);

J 1 J ₀ /cos» cJ „ l* ^{4 J}

/ds _ Γ¹ ds.cos γ _ 1 Г¹ ^

?

JLpi· c 15

i

о F cos ψ k-

COS Ψ =

к

T. о. в параболической А. для случая нескольких грузов Р, действующих одновременно, будем иметь:

5 ¹ Ра(1 — α)(Ζ²+la — а“)

-Ц- - Л л -- · (4)

8

15 с

8 /с/*²,

Для случая смещения опор на величину + dl

—15 Ес dl

⁸^Ф+8 W

или приближенно:

-15 Ecdl

8 fH

(5)

Для случая изменения темп-ры на +t°

_тт ± 15 Eact H_t =

или приближенно: Щ =

15 с

15 Eact 8f*

(6)

Величина g-^a представляет поправку, зависящую от влияния на деформацию нормальных сил N_x. Для равномерно распределенной нагрузки, при которой ось А.

является линией давления, надо в выражении (4) заменить Р через д da. Проинтегри-

15 с ровав это выражение и обозначив s=»

получим:

gl² gl² gl²

Η,

⁹ 8 Я1+0 8 f

8Д1+·)

gP

, или, по не-

gi²

e.

значительности ε: H_q=- ₀,.,

of of

распор в А. меньше, чем распор совпадающей с осью А. линии давления от постоян-

ql2

ной нагрузки, на величину е-^-· Если при

of

сборке А. дать ей при помощи клиньев

gl²

дополнительный распор *

8/‘ ’

то от по стоянной нагрузки этой арки ее линия давления совпадет с осью, распор будет равен Н=

gi²

8 f

и во всех сечениях будет только равномерное сжатие. Для создания

gl²

искусственного распора достаточно,

8

согласно уравнению (5), сблизить опоры gl³fe

на величину

Симметричная к р у г о в а я А. При среднем значении момента инерции I величина распора будет:

1) от действия сосредоточенных нагрузок:

^Η=^Σ[^Ρα (*-«);

2) от влияния изменения темп-ры:

_тт +16 ЕТ.

^И~ π I² *^t;

3) от изменения длины пролета на М:

н=——^-л г.

πΐ³

Линия влияния распора. Для определения ординат линии влияния распора надо в выражение (3) вместо М₀подставить значения момента в сечениях А. от груза Р=1. Если этот груз приложен на расстоянии а от левой опоры, то г Mr. ds га l — a ds

J _ ,J ₌j _x -_Ty+

l

/>

ds

ds

или, после подстановки -^у — du,

I ^y

rM₀ds I—a f^a, a ri

J I ^v~ ₀ ^dw* ^{x +} T J a^h,y Введя сюда конечные элементы s и конечные «упругие грузы» гю_у=~у, получим: rM₀ds I —. а i _п

J £~ У ~ I ~ Σ о 2 о ^Н У У ~~ ·

Это выражение представляет изгибающий момент в точке а под грузом Р=1 в простой балке пролетом I, нагруженной в центрах тяжести клиньев s упругими грузами s

му — -j- у · Для получения ординаты у_нлинии влияния Н, соответствующей поло жению груза а, нужно этот изгибающий момент еще разделить на выражение:

/y²ds, r ds хч ι, ν^^α s

Отсюда:

l-

11=

l

-Σο^Μν*+τΣ! ^wy(^l~^x)

ΣΙ ^v + 2!

(?)

i A

¹ о *

Отсюда следует, что эпюра моментов балки, нагруженной упругими грузами гс_у, пропорциональна линии влияния Н. Графически эта эпюра строится при помощи веревочного мн-ка (фигура 18) для упругих грузов w_v. Для положения грузов Р=1 в точке а,

г М ds

интеграл числителя выразится: J —⁰ — у== Wiy, где Ь,_у — полюсное расстояние соот

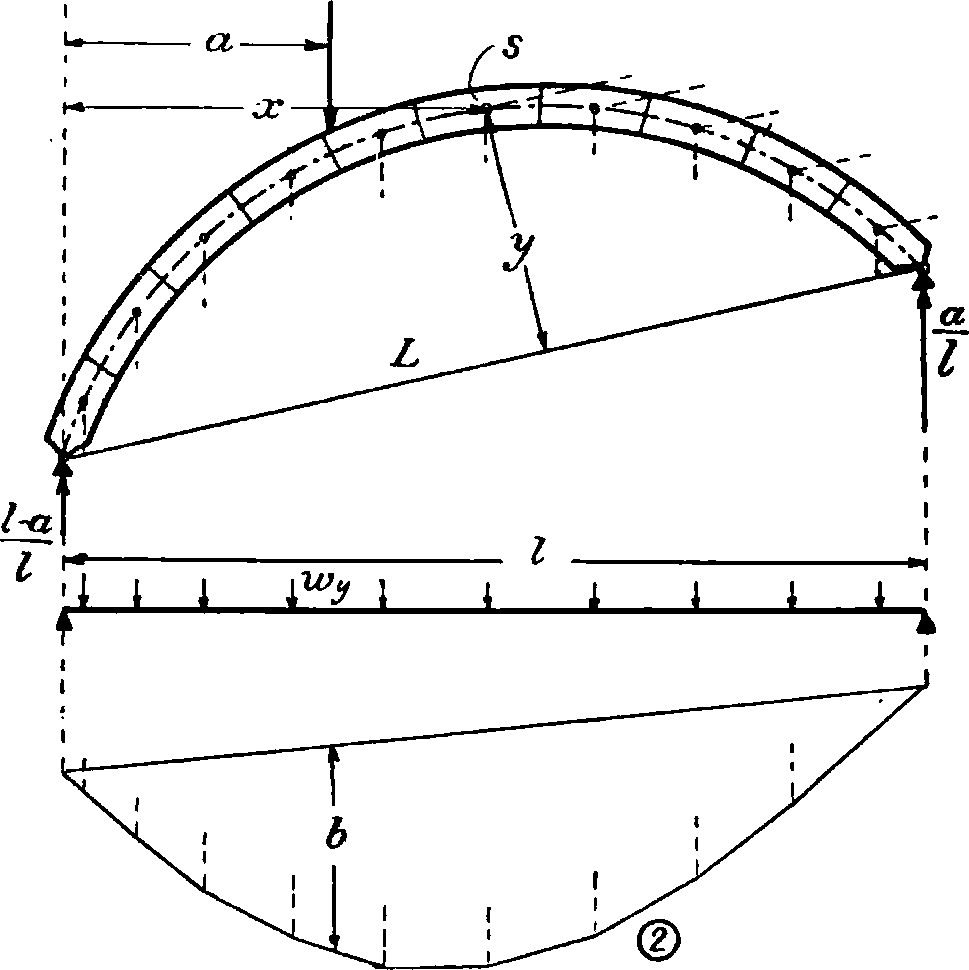
ветствующего силового мн-ка (1) для грузов w_y, а b — ордината веревочного мн-ка под грузом Р. Выражение Σ yWy тоже можно определить графически, как сумму моментов упругих грузов w_y, приложенных в центрах тяжести клиньев и направленных параллельно линии, соединяющ. опорные шарниры относительно этой линии. Для этого силовой мн-к (3) на фигуре 18 повернут так, что силы направлены параллельно прямой, соединяющей шарниры. Соответствующий веревочный мн-к отсекает крайними своими сторонами на этой соединительной прямой отрезок С, причем lyw_y=Ch_y. Отсюда мы получаем для груза Р=1 на расстоянии а от левой опоры:

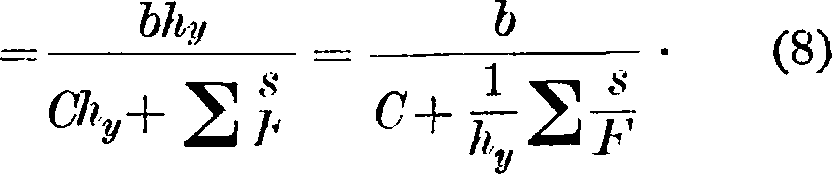
т. э. тп. I.

S3

Если к отрезку С прибавить отрезок ^К-Р^{ый нет}РУДНО вычислить, и полученный отрезок принять за единицу измерения для ординат b, то веревочный мн-к (2) даст непосредственно линию влияния Н.

Если нагрузка передается на А. через стойки, то в промежутках между двумя стойками (узлами) линия влияния должен быть прямолинейна. В мн-ке (2), вычерченном для конечных, хотя и малых элементов s, верны только те ординаты, которые лежат под границами элементов s. Отсюда следует, что разбивку этой А. на элементы следует сделать так, чтобы границы элементов оси совпадали с узловыми точками (со стойками,—фигура 19). При надобности эти элементы можно разбить на еще более мелкие части. В симметричной А. ординаты линии влияния распора Н можно найти вычисле-

Mf,yds_ _ ^ M₀Wy. Для вычисления нием

/-

целесообразно брать вместо одного два симметрично расположенных груза Р— 1 (фигура 20), к-рые, очевидно, дадут удвоенный распор; это дает преимущество в смысле более простого вы-^Λ“·ν ражения для мо-

-|——i— мента М₀. Во всех сечениях между грузами он постоянен и равен Ι.α; для сечений же слева и справа от обоих грузов М₀=1 х. Самое вычисление можно производить для одной половины А. Аналитический способ вычисления интеграла числителя для определения Н, при наличии симметрии, следует предпочесть графическому способу (по фигура 18). В этом

Гу" ds

случае, конечно, J — -=1 yw_y надо тоже

Фигура 20.

найти вычислением, что выгоднее всего произвести в форме таблиц.

Линия влияния ядрового момента. Эта линия, как уже указывалось выше, дает непосредственно невыгоднейшее расположение нагрузки и служит для вычисления предельных значений ядрового момента и напряжений в краях данного сечения. Линия влияния ядрового момента М_к для любого сечения двухшарнирной А.

получается как разность между линиями

Мок тт влияния —— и распора Н:

Ук

Mk=M_oi — Ну_к=у_к — lij ·

Линия влияния ядрового момента М_ок, определяемого как момент в простой двухопорной балке,—треугольник с вершиной под данной точкой if ядра сечения; отрезок, отсекаемый правой прямой этого тр-ка на левой опорной вертикали, равен х_кш Отложив, следовательно, на этой вертикали ордина-

Х_к ] ТлЬ ,. сл,

ту —легко вычертить тр-к (фигура 21).

Построив, кроме того, по предыдущему линию влияния Н, получим заштрихованную на фигуре 21 площадь влияния ядрового момента. Можно, при желании, отложить ординаты линии влияния от горизонтальной

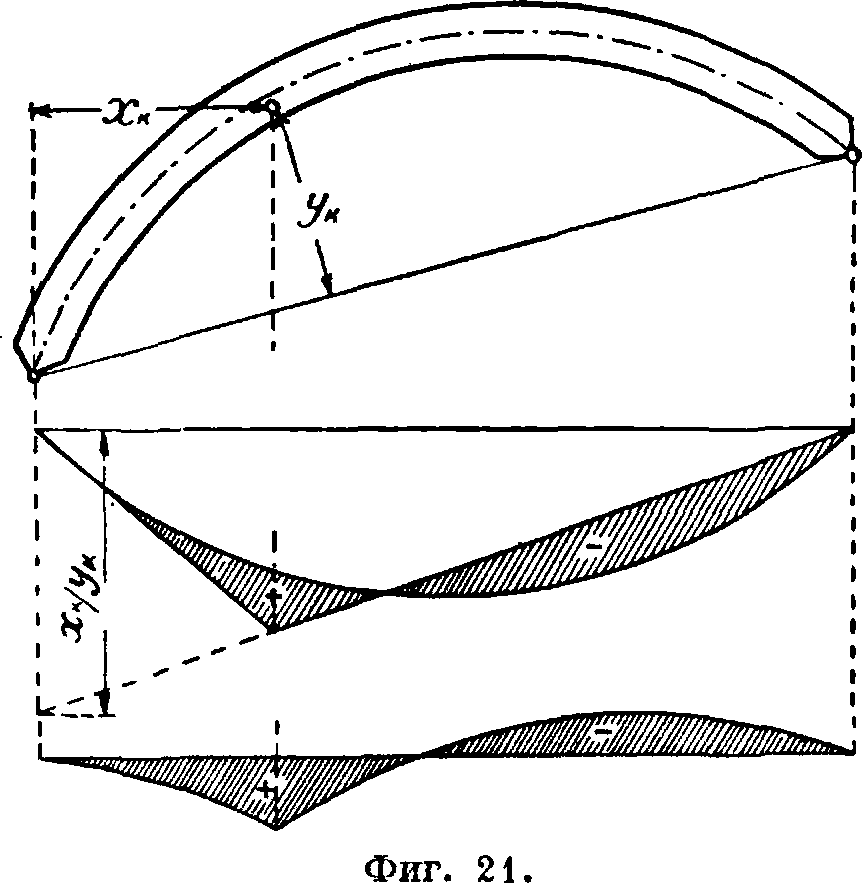
прямой, как показано на той же фигуре. Начертив один раз линию влияния if и к ней несколько тр-ков —5, можно по фигура 21

Ук *

получить линии влияния ядрового момента в нескольких сечениях при передаче нагрузки через стойки.

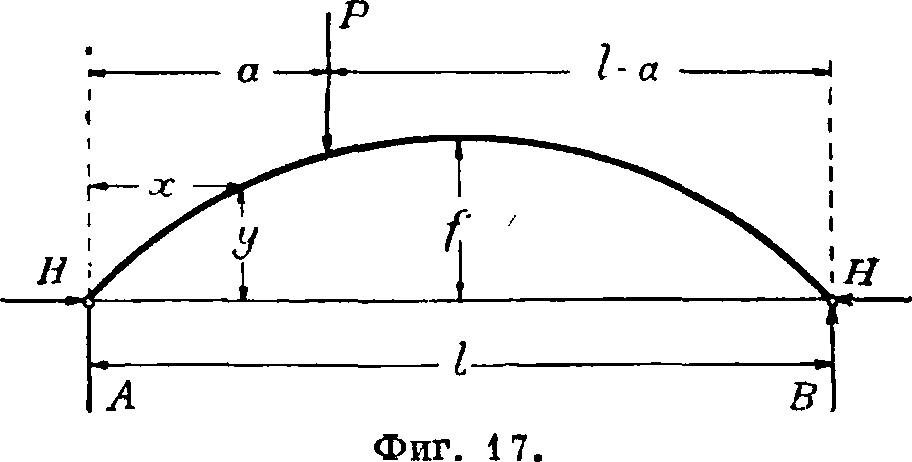
Двухшарнирная А. с затяжкой применяется, когда из строительных соображений нежелательно передать распор на опоры. Чтобы определить распор, воспринимаемый прямой горизонтальной затяжкой, связывающей пятовые шарниры, нужно в ур-ие (2) подставить: 0L=dl=-

HI

==упругому растяжению затяжки.

^2-Г 2

Если удлинение от темп-ры в А. отличается от удлинения в затяжке (например от солнечных лучей удлинение А. больше, чем удлинение затяжки, находящейся в тени),

Ή

то в формулу (1) надо вставить

Α₂-Γ₂

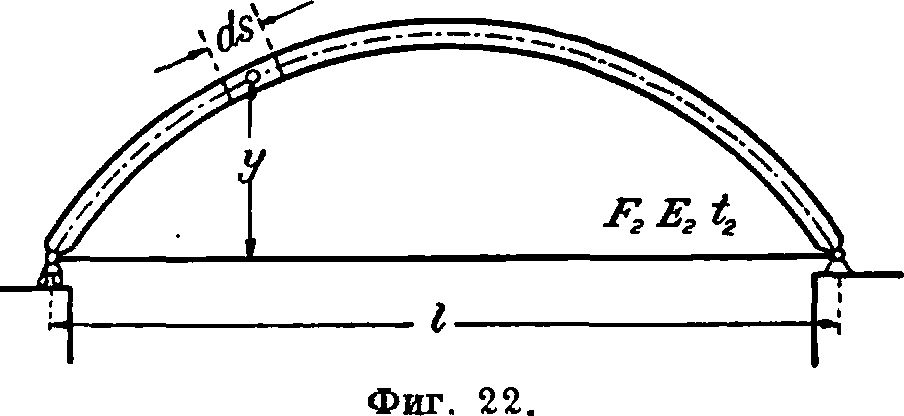
Сделав приведение, получим (фигура 22):

Н=

ГМ

J ~ у ds -f E<xl (t —1₂)

f³¥+f%+

ds. E_l_ E_B F*

(9)

Здесь E₂ и F₂ означают модуль упругости и площадь сечения затяжки, а Е — модуль упругости материала А. Одинаковое удлинение А. и затяжки не влияет на распор и не вызывает дополнительных напряжений. Так как А. с затяжкой всегда симметрична, то

распор в ней определяем непосредственно из ф-лы (9), для чего А. разбивается на элементы, концы которых лежат против подвесок, передающих нагрузку на А. При определении ординат линии влияния целесообразно вместо одного груза брать два симметрично расположенных груза Р=1, дающих удвоенную величину распора:

г М₀у ds V, M_nys

J—^-= 2j—j— > что позволяет делать вычисления только для половины А. При этом получаются те же упрощения для вычисления М₀ и сумм, какие были указаны в пояснении к фигура 20. Вследствие узловой передачи нагрузки от проезжей части подвесками, линия влияния Н имеет вид мн-ка с вершинами на узловых вертикалях (под подвесками). Поэтому достаточно располагать грузы Р — 1 против подвесок, а разбивку сделать так, чтобы концы элемента s приходились над подвесками. При графическом построении линии влияния ве-

/b1 V ds

—-, как и при отсутствии за-

тяжки, вычисляется как изгибающий момент в точке под грузом Р=1 для простой балки пролетом I, нагруженной упругими

s

грузами Wy=—j-y, приложенными в центрах тяжести клиньев. Действительно, если приложить груз Р=1 на расстоянии а от левой опоры, то как выражение

Σ-., s I—i ® ^ /i

^М° 1^{У =}~T~2j₀ ^Wy^X + -j2j_a ^wy(^l~^x)’

так и выражение

У“у можно перед ставить как сумму статических моментов горизонтальных упругих грузов w_y относительно линии, соединяющей опорные шарниры. Построение обоих интегралов или сумм показано на фигуре 23. Если к полученному графически отрезку С прибавить вели-1 I Е

j- -л, которые нетрудно

fly Е₂

вычислить, и суммарный отрезок взять за единицу для измерения ординат Ί-го веревочного многоугольника, то этот многоугольник может непосредственно служить линией влияния распора Н, так как

S

IF

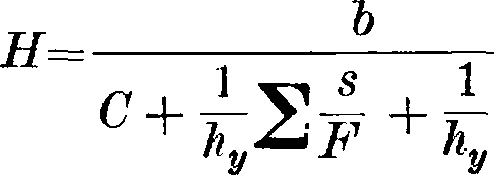
Ye

F а Е₂

Зная линию влияния распора, нетрудно построить линию влияния ядрового момента, ордината которой из ур-ия М_к=М_ок—Ну_к=

И_ок, У к

Н получается как разность ме-

М₀

жду ординатами линии — и линии влияния Н (фигура 23; площадь М_к заштрихована). При пользовании этой линией для расчетов ординат ее, необходимо помножать их на масштабный множитель у_к. Точки ядра сечения выбирают на одной вертикали, совпадающей с подвеской, хотя, строго говоря, в этом случае они принадлежат к двум сечениям А.

Для симметричной параболической А. с затяжкой, с постоянными или с принятыми за постоянные средними величинами cos ψ=с и Acos ψ — k, можно вычислить интегралы аналитически. Величина распора в такой А. определяется формулами:

52 Ра (I — а) (1²+1а — а“)

н=-^--^^-, (10)

8/7³|1 + * +

H_t=

15с Е

8/² F₂E₂15 cE«(t — t₂)

8 /д 1 + *+

15с Е

8/· F₂E₂

(Н)

Иногда затяжку делают ломаной. Ф-ла для распора Н при ломаной зцтяжке выводится из начала возможных перемещений.

За лишнюю неизвестную принимают горизонтальную составляющую Н усилия в затяжке, очертание которой делается по веревочному мн-ку, и составляют выражение работы силы Н= 1 фиктивного состояния (фигура 24) на перемещения действительного состояния (фигура 25). Эту работу можно представить себе вызванной натяжением в с/, икс. устроенном где-либо в затяжке:

o=2^s

Ss

EF

, ΓΜ_ΚΜ

Ei

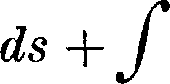
F_TN

EF

ds;

так как в фиктивном состоянии дейстт у< только одна сила Н= 1, то в пол>чеь выражение надо вставить: S=SH, М=1.у,

J I_X=M₀ — Ну; N= cos (у — «)=cos *> +

-)-tg a sin ψ и Ν_Χ=Η(cos γ+tg α sin y)+iV₀. В пологих арках можно приближенно Ад. eos φ выразить через Н, a N_x sin у tg α отбросить; тогда для усилия имеем ф-.чу:

*2Я

fMfd»

^н= yi ОТ» _| ftds r~ds ^(12> P J I J F

при чем знак Σ относится ко всем звеньям затяжки и подвескам, а интеграл—к самой А.

Фигура 24. Многоугольник сил при условии Н= 1.

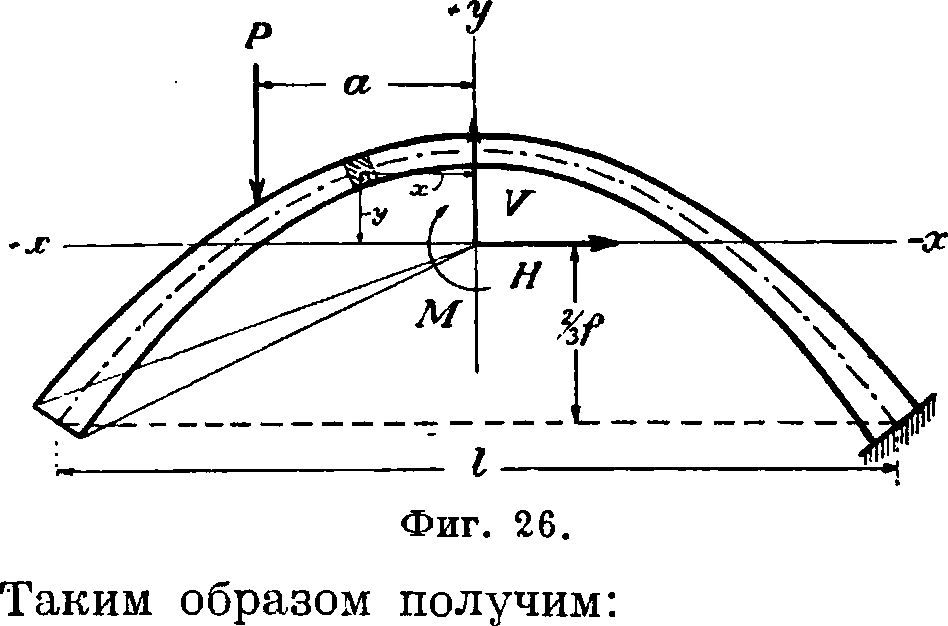
III. Бесшарнирная А. (с защемленными пятами) чаще всего встречается в сводах, почему и подробный расчет ее см. Своды, расчет. Здесь приведены только ф-лы для симметричной параболической бес-шарнирной А. с постоянными или с принятыми за постоянные средними величинами I cos ψ=β и Fcos<p=k. Если левую опору отбросить (фигура 26) и заменить действие ее некоторой реакцией, то нужно написать три ур-ия для определения величины, направления и точки приложения этой реакции. Перенося все компоненты (момент, вертикальную и горизонтальную составляющие) опорной реакции в центр тяжести упругих грузов dw—j (в «упругий центр тяжести»), к-рый надо представить жестко соединен-

Фиг 25. Действительное состояние. ным с опорным сечением А., можем составить следующие выражения:

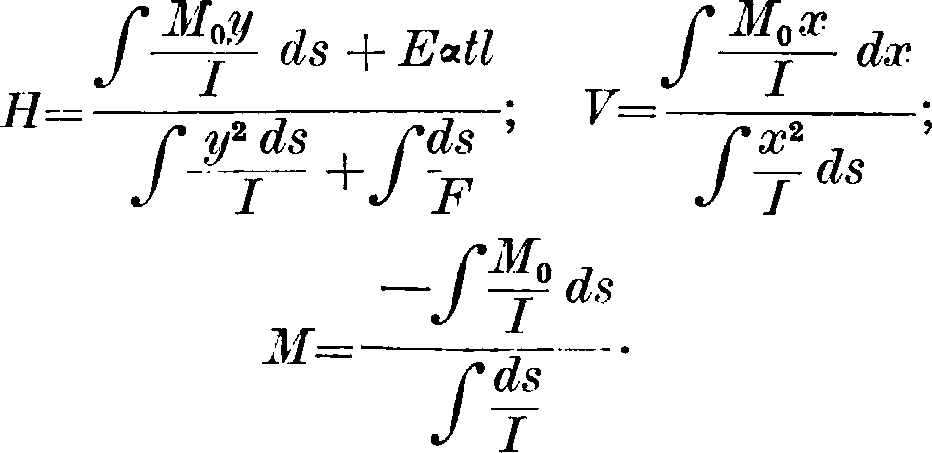
Интегралы вычисляются так же, как в симметричной параболической А. с двумя шарнирами (смотрите выше) и постоянными 1 cos у=с и Pcos <p=k. Сначала устанавливается упругий центр тяжести, к-рый определяется как центр тяжести упругих сил dw. В параболических А. он лежит на оси симметрии на расстоянии V» стрелы подъема от вершины параболы. Если взять начало координат в точке О, то ур-ие параболы будет:

f 4 f

f

(l² — 12 ж²).

I² ~ 3

Для одного груза P на расстоянии а от вершины:

ds r+^aP(a—x)!f 4 fx²

и." c ΊΓ ι*~

JM₀ у

f

4" i/* у² ds -Ut ¹

Иг

Pf

3d² 1 f²

3

A

dx

c 9 -i/,

₌±f4 45 c

(Ϊ_Γ

^ (l²—12 x²)²dx и T. д.

Я=

15

y^+lUP

(1+6 e) 4

45 C Eat

a²

H=-

4 f² 1+6* ’

^M=hz^Hi;Ah°f·

Если груз стоит на правой половине, то

15 с

a отрицательно; поправка е=^ ^. Можно опорную реакцию приложить не в упругом центре тяжести _г а в центре тяжести опорного сечения и туда же перенести начало

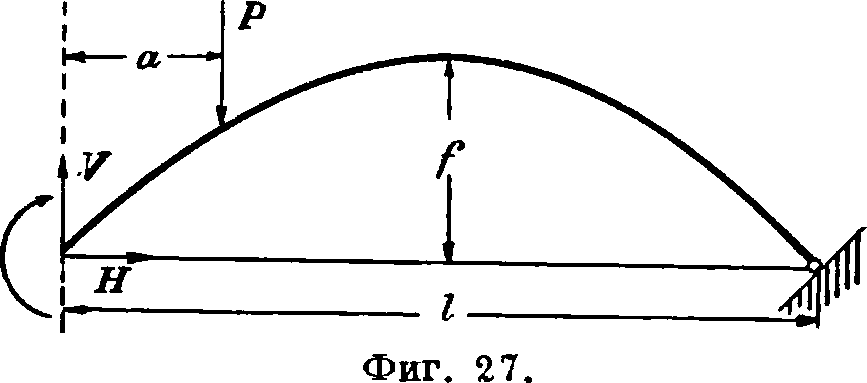
координат (фигура 27); тогда компоненты выразятся так:

^Н= (1 + 6 04/7" 2о ^Ра^¹~^а)²·

_тт 45 с Eat

Щ -

4 f² 1+6 e’

V= H^P(}^aff}+Zay,

_ЯуГ 15c Eat 2 „_TI

^M>=%7 TW.⁼ z^fH‘-

Из выражения M_t видно, что под влиянием изменения темп-ры в А. появляется реакция, состоящая из силы Щ, приложенной на 2.

расстоянии -^f от центров опорных сечений. Если принять по малости ε=0, то из сопоставления величин распоров в двухшарнирной и бесшарнирной арках можно видеть, что в бесшарнирной А. Щ в 6 раз больше, чем в двухшарнирной; поэтому, при прочих равных условиях, температурные напряжения получаются в пяте бесшарнирной А. в 4 раза", а в ключе в 2 раза больше, чем в А. двухшарнирной.

Простые А. сквозные.

Они представляют собою фермы, опоры к-рых, кроме вертикальных реакций, воспринимают распор. Расчет их см. Фермы, статически определимые и статически неопределимые.

Лит.: Проскуряков Л., Строит, мех.,

ч. I, ГИЗ, 1925; Мюллер-Бреслау Г., Графил. статика сооружений, τ. 2, ч. II, пер. Г. Криво-шеина, СПБ., 1912; Прокофьев И. П., Теория сооружений, ч. I, М., 1926; Castigliano Alb., Theorie de l’dquilibre d. systfimes diastiques, Turin, 1881; Weyrauch J., Elastische Bogentrager. Stuttgart, 1911; Miiller-Breslau H., Die graphische Statik d. Baukonstruktionen, B. 2, Τ. II, Lpz., 1908; Μ u 11 e r - В r e s 1 a u H., Neuere Metho-den d. Festigkeitslehre, Lpz., 1913; Ritter W., Anwendungen d. graph. Statik, Τ. IV, Der Bogen, Zurich, 1906; Handbuch d. Ingen. Wissensch., B. 6, Τ. II,—Theorie d. eisernen Bogenbriicken usw., Lpz., 1925: Schaechterle K. W., Elastische Bogen, Bogenstellungen u. mehrstielige Rahmen, B., 1912; Strassner A., Neuere Methoden zur Statik d. Rahmentragwerke und d. elastischen Bogentrager, B. 2, B., 1921; Strassner A., Der durchlaufende Bogen auf elastischen Stiitzen, B., 1919.