> Техника, страница 17 > Аэродинамика

Аэродинамика

Аэродинамика (расчет самолета). Аэродинамический расчет самолета дает возможность конструктору разрешить задачу об аэродинамических характеристиках данной машины: об установившихся скоростях самолета при различных режимах полета (на всех возможных для данной машины высотах), о скороподъемности и потолке данной машины.

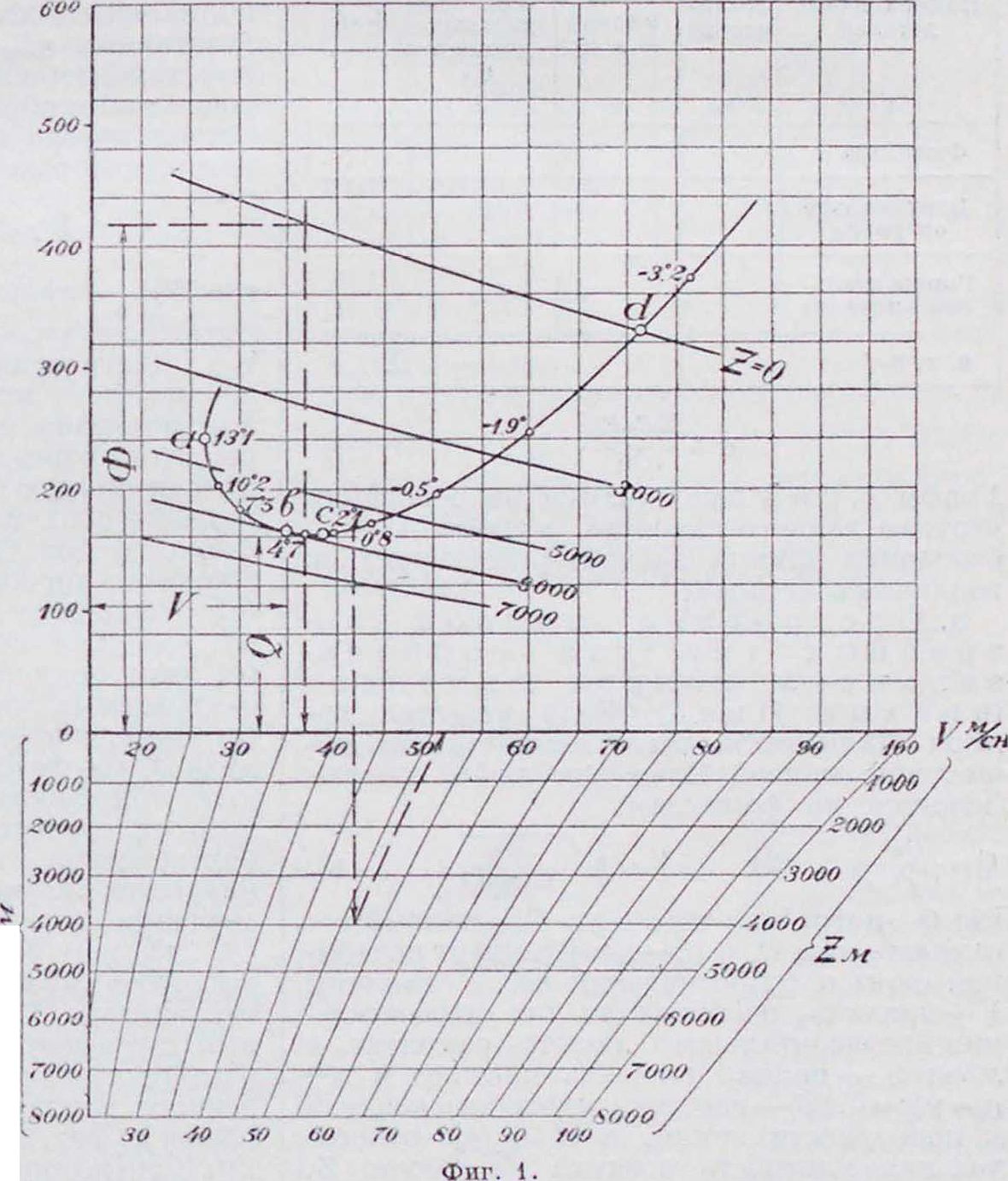
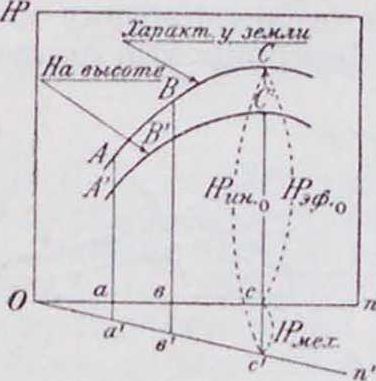
Решить эту задачу конструктор может различными методами в зависимости от требуемой степени точности. Одним из хороших методов аэродинамического расчета самолета, получившим в настоящее время большое распространение, следует считать графоаналитический метод, заключающийся в наложении характеристики винтомоторной группы на кривые Пэно (кривыми Пэпо называются кривые тяг, или мощностей, которые потребны для установившегося горизон-тальн. полета самолета); он дает достаточную точность. На фигуре 1 кривая abed изображает кривую Пэно в координатах тяги К| и скорости, а ряд пересекающихся с ней кривых“ изображает тяги, развиваемые винтомоторной группой на различных высотах полета самолета. Совмещение этих кривых на одном графике, при дополнительной сетке масштабов для скоростей на различных высотах Z, позволяет довольно быстро определить все важней

• Обыкновенно зтп кривые весьма близко пгдхо-лнт к прямым и приближенно они всегда принимаются за прямые.

шие аэродинамические характеристики самолета. Предварительные расчеты, которые необходимы для построения кривой Пэно, и высотные характеристики винтомоторной группы, при отсутствии продувки всей модели самолета, удобно производить в нижеследующем порядке:

1. Построение поляры Лилиенталя коробки крыльев самолета производится по методам теории индуктивного сопротивления (смотрите).

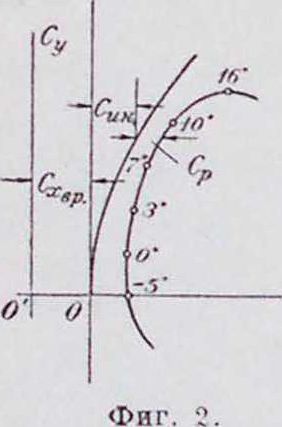
2. Подсчет вредных с о п р о-т и в л е н и й. Для получения поляры Лилиенталя всего самолета следует к сопро тивлению крыльев прибавить еще дополнительное, т. н. вредное, сопротивление ОО, создаваемое деталями самолета (смотрите фигура 2).

Коэффициент этого дополнительного сопротивления определяется формулой:

С,=?-·£-, (1)

^хвр. Ь ^{4 7}

где S’—площадь крыльев в .я², а а—площадь эквивалентной (по сопротивлению) плоской пластинки (стоящей нормально к потоку) в м², определяемая путем подсчета и

суммирования сопротивления отдельных деталей. Сводку вредных сопротивлений самолета изображают в виде следующей таблицы:

Наименование деталей	Коли чество	Общая нлощ. миделя F в м»	Коэфф. сопротив-лен. отдельных деталей Сх	CXF
1	2	3	4	5
Фюзеляж.
Вертикальное оперение.
Горизонтальное оперение
и т. д.				Σ(·ΧΡ

ΣC_TF

α=--

U,6t

Графы 1, 2 и 3 заполняются на основании чертежа данного самолета, а графа 4 — на основании данных лабораторных продувок различных деталей.

3. Построение кривой потребных тяг для горизонтального полета самолета (к р и в ы e II э н о). Если известна поляра Лилиенталя всего самолета, то вычисление кривой Пэно для любой высоты делается по формулам:

e-<§s· <²> (3)

где Q—потребная тяга в килограммах; G₀—полный вес самолета в килограммах; С_у и С_х—коэффициент подъемной силы и сопротивления всего самолета; V—скорость, необходимая для осуществления горизонтального полета самолета в м/ск; S — полная площадь крыльев в м^г; 6о=У 9=0,125—массовая плотность воздуха у поверхности земли, a A—qJq₀—относительная плотность воздуха на высоте Z. Значение Δ для различных высот следует брать из стандартной атмосферы (смотрите Атмосфера стандартная). В виду того, что с высотой меняется только скорость, потребная для горизонтального полета самолета, можно ограничиться вычислением кривой Пэно только для случая, когда /1=1, то есть для полета близ земли, а изменение ско ростей при полетах на высоте можно учитывать дополнительными масштабами оси абсцисс (смотрите фигура 1). Для построения этой сетки масштабов скоростей для различных высот следует для каждой высоты начальный масштаб оси абсцисс уменьшать

Читать скорости на высотах следует так, как показано на фигуре 1, т. о, если на уровне моря скорость самолета V=42 м/ск, то на высоте 4 000 метров она будет равна 51,5 .и ск.

4. Высотная характерист п-к а мотора. Если высотная характеристика мотора, то есть зависимость мощности от числа оборотов, неизвестна из опытов, то ее приходится строить приближенно. При таком построении считают, что индикаторная мощность мотора изменяется пропорционально плотности воздуха, а механические потери не зависят от высоты и пропорциональны числу оборотов мотора. Механическим коэффициентом полезного действия мотора, г)_мсх, молено задаваться, считая, что у современных стационарных моторов при нормальных числах оборотов 9*«.=0,88, а у ротативных η_Μ(χ. es 0,80. Построение высотной характеристики мотора обычно производят таким образом: находят механические потери мотора при нормальном числе оборотов, которые определяются формулой:

IP

мех.

HV

о

1 ^— Чмех·

»

Чмех·

(4)

Обыкновенный люпгор О

где IР_Эф. —эффективная мощность мотора,

соответствующая нормальному числу оборотов. Далее откладывают эти потери в том же масштабе мощности снизу оси абсцисс, как показано на фигуре 4, и, соединяя конец этого отрезка с началом координат, получают прямую Ол, выражающую величину механических потерь мотора при всех числах оборотов. Ординаты Ли, ВЬ и Со изображают индикаторные мощности мотора; умножая величины этих ординат (отсчитываемых от осп On) на плотность воздуха Δ, соответствующую той высоте, для которой строится характеристика, и откладывая полученные значения вверх от оси On, находят искомую высотную характеристику мотора. Примерный вид высотной характеристики обыкш >-венного мотора изображен на фигуре 3 (вверху). Если мотор с повышенной степенью ежа- О¹--п гия и может сохра- фигура з. пять свою мощность до некоторой высоты, то прежде всего нужно знать эту высоту. Построение же характеристики такого мотора при больших высотах делается так же, как и на фигуре 4, но только вместо действительной земной

Высотный .мотор

кривой ЛВС берется кривая эффектна. мощности такого мотора при работе его у земли на полном газе при условии отсутствия детонации (смотрите), то есть при полном открытии дросселя. Такая мощность называется эквивалентом мощности мотора у земли и указывается фи рмой. Примерный вид высотной характеристики мотора изображен на фигуре 3 внизу.

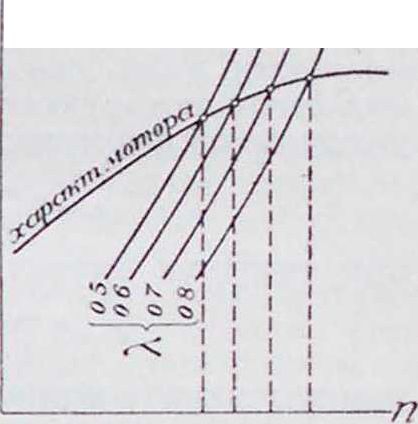
5. II од бор в и Ητα. Для подбора винта к самолету из имеющихся сери и испытанных в лаборатории винтов необходимо знать число оборотов мотора, мощность мотора и скорость полета, при которой желательно иметь максимальный коэффициент полезного действия пинта. Указанная выше скорость называется расчетной скоростью вин та. Число оборотов и мощность мотора при подборе винта всегда бывают известны, и, следовательно, остается выбрать только расчетную скорость винта. Рассмотрим два возможных при этом случая: 1) Самолет с обыкновенным мотором. Когда машина при заданной мощности мотора должна развивать наибольшую скорость горизонтального полета, то расчетной скоростью винта должна быть V_mar, которая может быть определена предварительными прикидками. Если машина, по заданию, должна хорошо забирать высоту и должна иметь возможно больший потолок, то за расчетную скорость винта следует принимать наивыгоднейшую скорость для подъема. На фигуре 1 эта скорость обыкновенно лежит вблизи точки с кривой Пэно, а у современных самолетов ее часто принимают равной 0,7 V_!ltax. Большинство же современных самолетов с большим избытком мощности имеет расчетные скорости винтов: *Vu.=0,8-0,9 V_max. Зная расчетную скорость винта, мощность и число оборотов мотора, а также имея характеристики различных серий испытанных винтов, задаваясь диаметром, выбирают из этих серий винт, дающий V_max. Если характеристики испытанных серий винтов изображены на логарифмических графиках, то подбор винта легче всего производить, пользуясь ими (смотрите Винт воздушный). 2) С а м о л е т с в ы с о т и ы м мот о ром. Подбор винта к самолету с высотным мотором сложнее, так как винт, рассчитанный на земную скорость, на высоте будет разгоняться, а винт, рассчитанный на определенную скорость на высоте, может оказаться несколько тяжелым при взлете и при полетах близ земли. Решение вопроса о расчетной скорости винта в таких случаях находят прикидками, которые удобно производить способом Рита. Если мотор может сохранять свою мощность до больших высот, то подбор винта из серии обыкновенных винтов иногда может оказаться невозможным. Тогда приходится проектировать специальный винт с поворотными лопастями.

Фигура 4.

6. Построение характеристики винтомоторной группы. Для построения высотной характеристики наносят на график значения высотных мощностей мотора. Когда винт выбран по логарифмическим графикам, то сочетание его характеристики с характеристикой мотора проще и быстрее делать по способу Рита. Во всех остальных случаях можно указать на следующий способ: задавшись рядом подходящих значений для характеристики режима полета А =, по кривым коэффициента мощности β и коэффициента полезного действия винта η определяют ряд соответствующих им значений β и η. По этим величинам вычисляют требуемую для винта мощность ΙΡ_βкоторая для каждого значения А будет равна

IP„.=^ D^{5 * 7}n³=Const- · η³. (δ)

Так как число оборотов всей винтомоторной группы неизвестно, то для каждого данного значения А //>

fuyt,Г псраоо.-ш

нужно на графике характеристики мотора(фигура5) нанести построенные по формуле (5) кубические параболы мощности винта; тогда точки пересечения» этих парабол с характеристикой мотора определят искомые числа оборотов и развиваемые мотором мощности при различных ре-

у жимах А =—гг. Зная нее м,—число об/ск.,

n_sL> *

D—диаметр винта в м и А, находят скорости полетα= Арг₈₁П; V„— A,n_S)L> и т. д. и соответствующие этим скоростям тяги, развиваемые винтомоторной группой

. .X, · 7 5

Фигура 5.

N i*75 ,_г. JV₂.75.

^Ф1=»?1 ν ; ^Φ2=»?ϊ

У,. -3--/3 _Vj. -3 /3 y₃

и T. д. Для построения характеристики винтомоторной группы на высоте следует брать вместо характеристики мотора у земли его высотные характеристики, но толь-ф_нг ко изменять мощ ности, потребляемые винтом, пропорционально относительной плотности воздуха Δ, значение которой следует брать из стандартной атмосферы. Постро-

. у еннаятаким образом полнаяхарактеристика винто моторной группы будет иметь вид, который изображен на фигуре 6.

7. Учет взаимного влияния винта и частей самолета. Прежде чем нанести найденную высотную характеристику винтомоторной группы на график фигура 1, следует ее исправить на

ФПГ. 6.

взаимное влияние винта и частей самолета, которое заключается в следующем: а) Влияние винта на лобовое сопротивление частей самолета. Можно приближенно считать, что от влияния струи винта лобовое сопротивление фюзеляжа П₀ увеличивается в отношении

£⁼¹ + (^{1 +} пУ⁷

В

(С)

при тянущих винтах и R

(-)

при толкающих винтах. Лобовое сопротивление остальных частей самолета, находящихся в струе винта, возрастает в отношении

#,-1 + 2 В, (8)

где В — коэффициент нагрузки на ометае-мую винтом площадь, С_х—коэффициент сопротивления фюзеляжа, б) В л и я н и о частей самолета на работу в и н -т а. На винт влияет главным образом только фюзеляж. Его влияние можно учитывать, сдвигая кривые коэффициента тяги и мощности вдоль оси А в сторону увеличения А на некоторую величину εΑ, где ε определяется по формуле:

:(9)

при тянущих винтах и

_ЛГ

F У 1 К И

(10)

при толкающих винтах. Здесь σ_ι — поверхность эквивалента, плоской пластинки для фюзеляжа в .и², F — ометаемая винтом площадь в JH², S—площадь миделя фюзеляжа в .н². Коэффициент полезного действия винта на самолете V,._aM. выражается через коэффициент полезного действия изолированного винта η„₃_ таким образом:

_ „ Λ а-0,64я! 2·0,64<τΛ.

= + F - F -) ’ (^П)

где σ₂ — площадь эквивалентной плоской пластинки для остальных деталей (кроме фюзеляжа), находящихся в струе винта. Индексы А и А при η показывают, что винт на самолете работает при режиме А, а изолированный винт работал бы при режиме А. Связь между А и А такая:

А=А (1 + ε)

Коэффициент а, входящий имеет значение:

0=1+ ¹

(12)

в формулу (11),

(13)

(14)

при тянущих винтах и ^а=зс;

при толкающих винтах. Следовательно, когда характеристика винтомоторной группы дана в координатах тяги и скорости, учет обдувки можно производить по следующим формулам:

Фj=Ф (1

а 0.61 п,	1,29 σ2
F	F )

) (15)

^=7(1 + 8), ne)

то есть все точки abc кривой полезных тяг

(фигура 7) следует опустить в положение аЬс и затем сдвинуть вправо в положение а" Ь’с". Кривая, которая проведена через точки а" Ь”с", и будет окончательной кривой полезных тяг с учетом всех влияний. Проделывая те же операции и с высотными кривыми, получают полную характеристику винтомоторной группы. Построив эти окончательные кривые 0,_;. полезных тяг на фигуре 1, но только таким образ., чтобы их масштабы по оси абсцисс для каждой высоты соответствовали масштабам сетки,

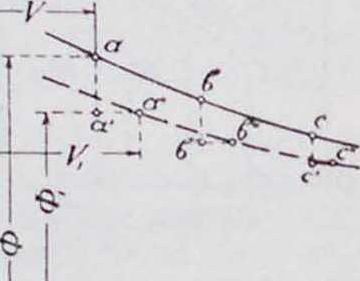
получают требуемое совмещение

КРИВОЙ ПЭНО С Фигура 7.

высотной характеристикой винтомоторной группы (фигура 1), что дает возможность довольно быстро найти все аэродинамические характеристики самолета.

8. Определение вертикальных скоростей, потолка и скороподъемности самолета. Барограмма. Вертикальную скорость при подъеме самолета обыкновенно определяют по наибольшему избытку мощности, развиваемой винтомоторной группой, над мощностью, потребной для горизонтального полета. Этот наибольший избыток мощности определяется из фигура I несколькими прикидками в области Ьс кривой Пэно по формуле: *

ЛТ=ΦΥ - QV=(Ф - Q) V. (17)

Вертикальная скорость самолета выражается формулой:

и

ΔΤ _ (0>-Q)V G о Go

м/ск,

(18)

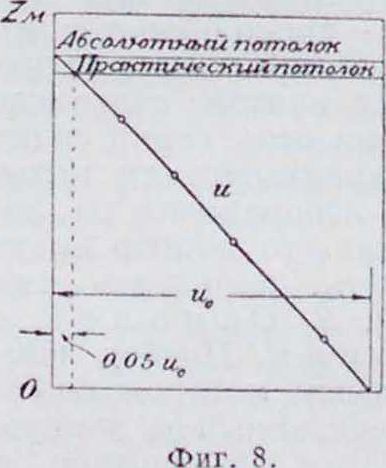
где G₀ — полный вес самолета в килограммах. Когда вертикальные скорости определены на нескольких высотах, их значения наносят на график в функции высоты (фигура 8) и через полученные точки проводят главную кривую, которая в пересечении с осью ординат определяет абсолютный потолок самолета. Тот же график (фигура 8) позволяет найти и практический потолок самолета, который в СССР определяется предельной вертикальной скоростью:

Unped.=°>°5 и₀, (19)

где г<₀—наибольшая вертикальная скорость у земли (на уровне моря). У самолетов, которые снабжены обыкновенными, невысот-

* Формула (17) приближенная, т. и. пней не учтено плинние наклона траектории полета; по ошибка в самом крайнем случае (истребитель с большим избытком мощности) не будет более 3%.

ними моторами, закон изменения с высотой вертикальных скоростей обыкновенно выражается прямой или весьма близкой к ней пологой кривой. В этом случае для вычисления скороподъемности самолета можно пользоваться формулой:

:0,0384 ^я lg-ί

U° j

(20)

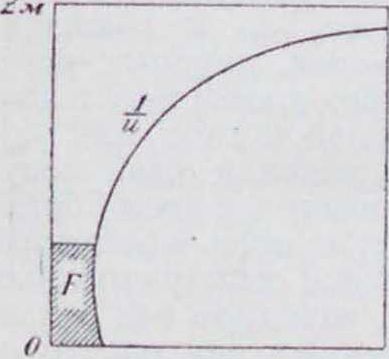
где II—абсолютный потолок в м, и_в— вертикальная скорость в начале подъема в м/ск, —время подъема в минутах на желаемую высоту Z. Если закон изменения с высотой вертикальных скоростей выражается не прямой, а какой-либо кривой, как на фигуре 9, что может иметь место при высотных моторах, то вычисление скороподъемности делают таким образом: вычисляют и строят в функции высоты значения величин, обратных вертикальной

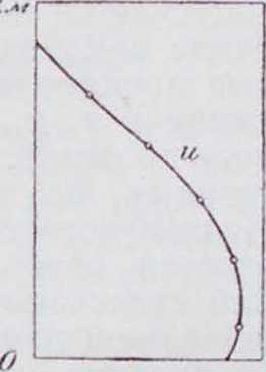
Фигура 9.

скорости,

как это сделано для примера на фигура 10, и планиметрируют площадки F, которые в некотором масштабе выражают время подъема на желаемую высоту. Найденные значения времени подъема на различные высоты изображают графически. Такие графики называются барограммами подъема самолета.

9. Определение скоростей на различных режимах полета самолета. Максимальные скорости горизонтального полета самолета на различных высотах определяются точками пересечения кривой Пэно с кривыми тяг, развиваемых винтомоторной группой при малых углах атаки. Так, например, на фигуре 1 точка d определяет максимальную скорость горизонтального полета близ земли (на уровне моря). Точка с кривой Пэно, соответствующая минимуму тяги, потребной для установившегося горизонтального полета, определяет так называемым наивыгоднейшую скорость самолета. Точка b кривой Пэно, соответствующая минимуму затрачиваемой на полет мощности, определяет экономическую ско-_г рость самолета. Hali конец, точка о кри-Фнг. ία. вой Пэно определяет ту минимальную скорость самолета, при которой для него еще возможен установившийся горизонтальный полет. Эта скорость называется посадочной скоростью и определяется формулой (3) при максимальном значении коэффициента подъемной силы Сц„_шх.

Читать все вышеупомянутые скорости на высотах при помощи сетки высотных масштабов следует так, как показано на фигуре 1 стрелками и пунктиром (штриховой линией).

Лит.: Александров В. Л., Аэролипамнче-скик расчет аяропланов, Макиз, Москва, 1922; Ю р ь-е в Б. Н., Крылья типа Юнкере.—Новый прием аэродинамического расчета самолетов, над. Высшего поен, редакц. совета, М., 1922; Александров В. Л., Пассажирский самолет ЦАГИ АК 1. Его проектирование, постройка и испытание. (Материалы но проектированию самолетов.) «Труды ЦАГИ», выпуск 17, изд. НТО ВСНХ, Москва, 1925; Юрьев Б. Н. Воздушные греОпые винты (пропеллеры), «Труды ЦАГИ», вып. 10, изд. НТО ВСНХ, Москва. 1925; Юрьев Б. II., Индуктивное сопротивление крыльев аэроплана, «Труды ЦАГИ», вып. 20, изд. НТО ВСНХ, М., 1926; Лиганд К. А. и Лыко ш и н II. А., Графо-аналитический аэродинамический расчет самолета по методу инж. Чадвика, изд. КУБУЧ, Ленинград, 1925; Ветчин кин В. П., Каменев с. и. и Ч е н ц о в Н. Г., Динамика полетов, «Труды ЦАГИ», вып. 26, изд. НТУ ВСНХ,

М., 1927; Соколов II. II., Теории авиации (в элементарном изложении), изд. Высш. школы вспомог, служб Кр. возд. флота, М., 1924; Б аде р Г. (перевод, и дополи. Лыкошина), Введение в аэропланостроение, изд. КУБУЧ. Л., 1326; Фадеев И. Н., Аэродинамический расчет планера, изд. Авнахим, М., 1926;

К с а к д р о в Д. Н., Аэродинамический расчет аэропланов, изд. АвиосекцииХарьковского технолог, ин-та. 1925; 1 e V i Hers R., La dynainique de 1avion, Paris, 1920; К 1 e in i n A., A Text-book of Aeronautical Engineering, London, 1925; В a i г s t о w L·., Applied Aerodynamics, London, 1920; Booth II. Aeioplane Performance Calculations, N.Y., 1921; Technical Reports of the Aeronautics Advisory Committee, London, 1916—1925; Reports of the National Advisory Committee for Aeronautics, Wsh., 1917—1925; Fu c h s R. und II о p f L., Aerodynamik, Handbuch der Flug-zeugkunde, B., 1922. А. Че».