> Техника, страница 95 > Аэродинамика

Аэродинамика

Аэродинамика, часть гидродинамики, изучающая движение сжимаемых жидкостей (газов) и движение тел, погруженных в эти жидкости. А. разделяется на теоретическую (смотрите Аэродинамика, т. 1), опирающуюся на общие законы механики, и экспериментальную, или прикладную, А., основанную на опытных данных и дополняющую общие выводы теоретич. А. Свое технич. приложение А. получает в авиации, где она касается изучения обтекания твердых тел определенных форм и нахождения сил, действующих на эти тела.

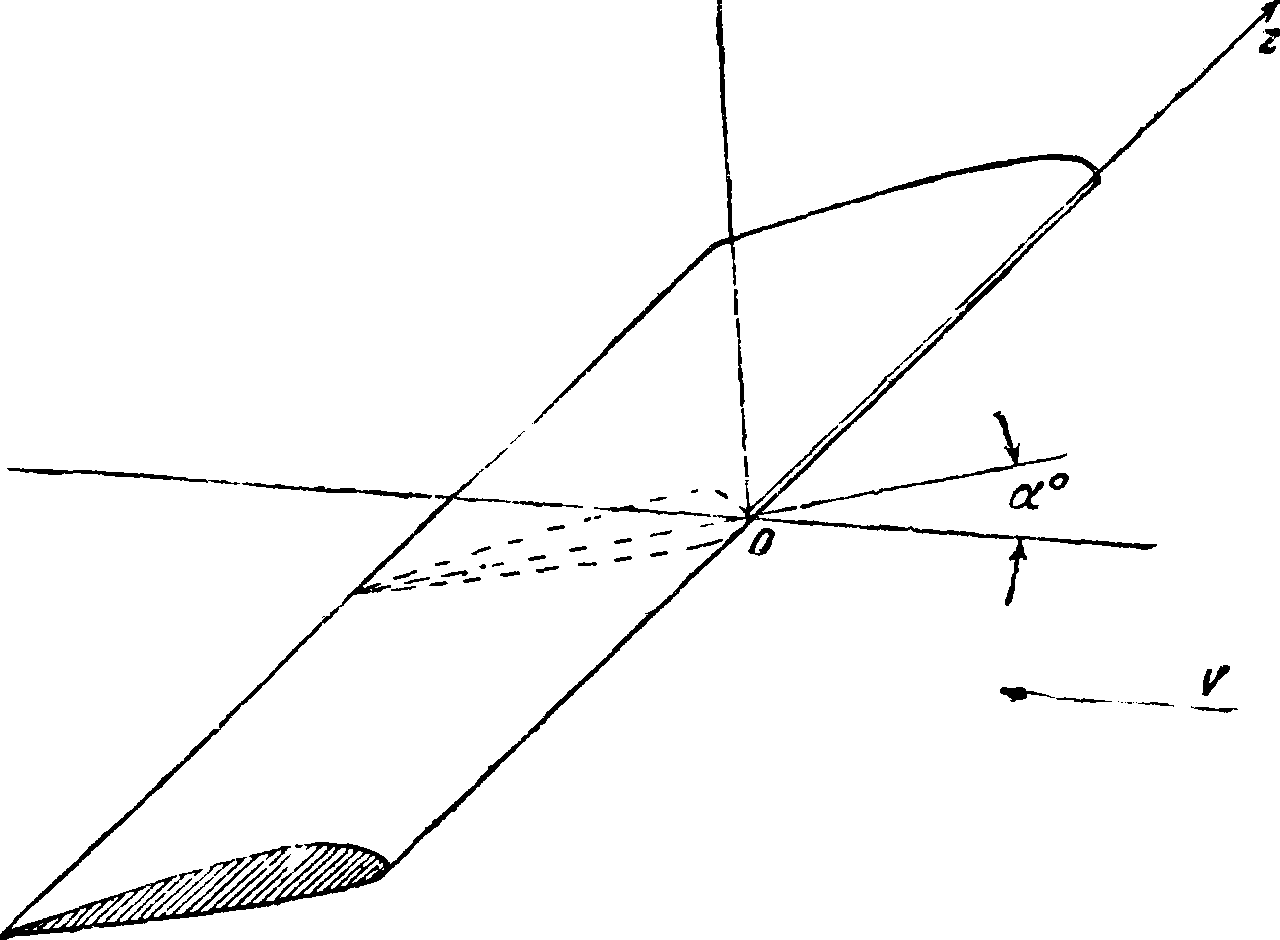
I. Система координат при испытаниях моделей в аэродинамических трубах. При аэродина-мич. исследованиях б. ч. приходится производить испытания тел с одной или несколькими плоскостями симметрии (модели крыла, самолета, дирижабля, шара, цилиндра и т. д.). Модель располагается в воздушном потоке обычно так, что ее плоскость симметрии совпадает с направлением потока, причем нулевое или начальное ее положение фиксируется тем или иным способом (например для модели крыла или самолета начальное положение определяется совпадением хорды крыла с направлением скорости потока). Система взаимно ортогональных координатных осей, к которым относятся аэродинамич. силы и моменты, построена след. обр. (фигура 1): ось х направлена по скорости потока, ось у лежит в плоскости симметрии модели и направлена перпендикулярно к скорости потока, ось л направлена перпендикулярно к плоскости симметрии модели, то есть к плоскости ху. При испытании крыла начало координат помещается обычно на передней кромке крыла, а при испытании модели самолета — *в его ц. т. Если модель симметрична и симметрично расположена относительно потока, то равнодействующая приложенных к модели аэродинамич. сил лежит в плоскости симметрии модели, и для ее определения достаточно знать две ее проекции на оси х и у и момент относительно оси z. Если симметрия так или иначе нару

шена, например путем отклонения элеронов или руля направления или путем повертывания всей модели относительно оси х или у, то аэродинамическая равнодействующая не будет уже лежать в плоскости ху, и для ее определения необходимо знать все шесть компонентов: проекции равнодействующей на три оси и моменты равнодействующей относительно трех осей.

Фигура 1.

II. Обозначения, размерности и определения основных аэродинамических величин. а° [град.] — угол атаки, — угол между направлением скорости потока и плоскостью крыла, проходящей через центральную его хорду (фигура1).

F, V [м/ск] — скорость потока. у[кг/м? — весовая плотность воздуха. д[м/ск²] — ускорение силы тяжести.

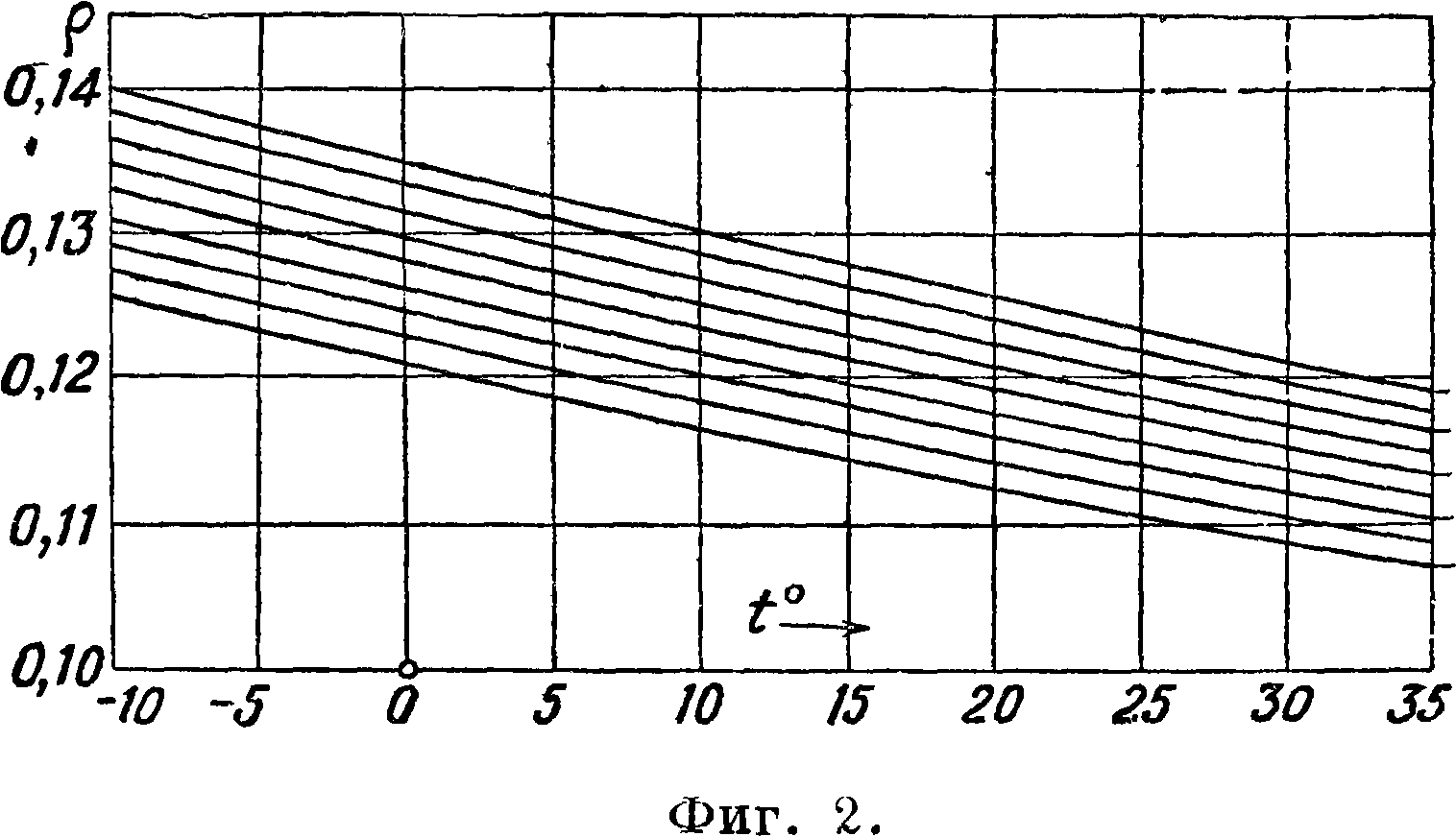
ρ — — [кг-ск²/м“]— плотность воздуха. Зависимость ρ от Г и давления (в миллиметров рт. ст.) представлена на фигуре 2.

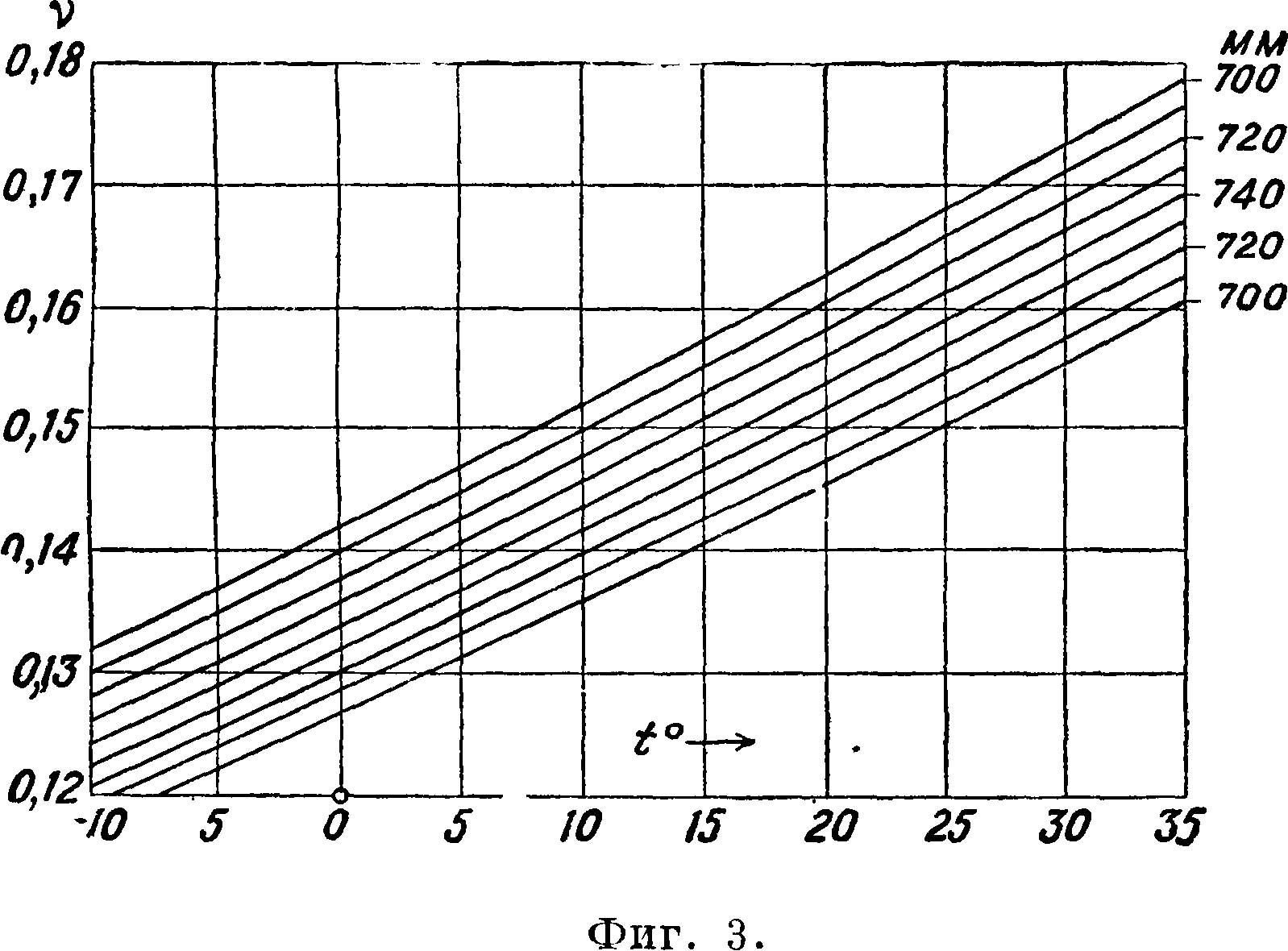
р[кг-ск/м²]— коэф. вязкости воздуха. ν=~ [м²/ск]—кинематич. коэф. вязкости воздуха. Зависимость ν от t° и давления (в миллиметров рт. ст.) представлена на фигуре 3 (на диаграмме размерность γ дана в см^у/ск).

q — [кг/м²] — скоростной напор или дина-

мич. давление воздуха. р[кг/м² — статич. давление воздуха.

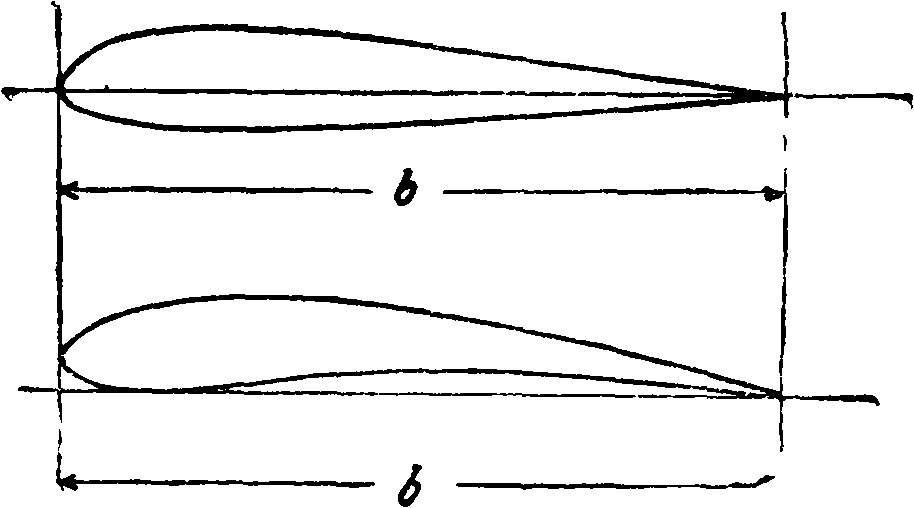
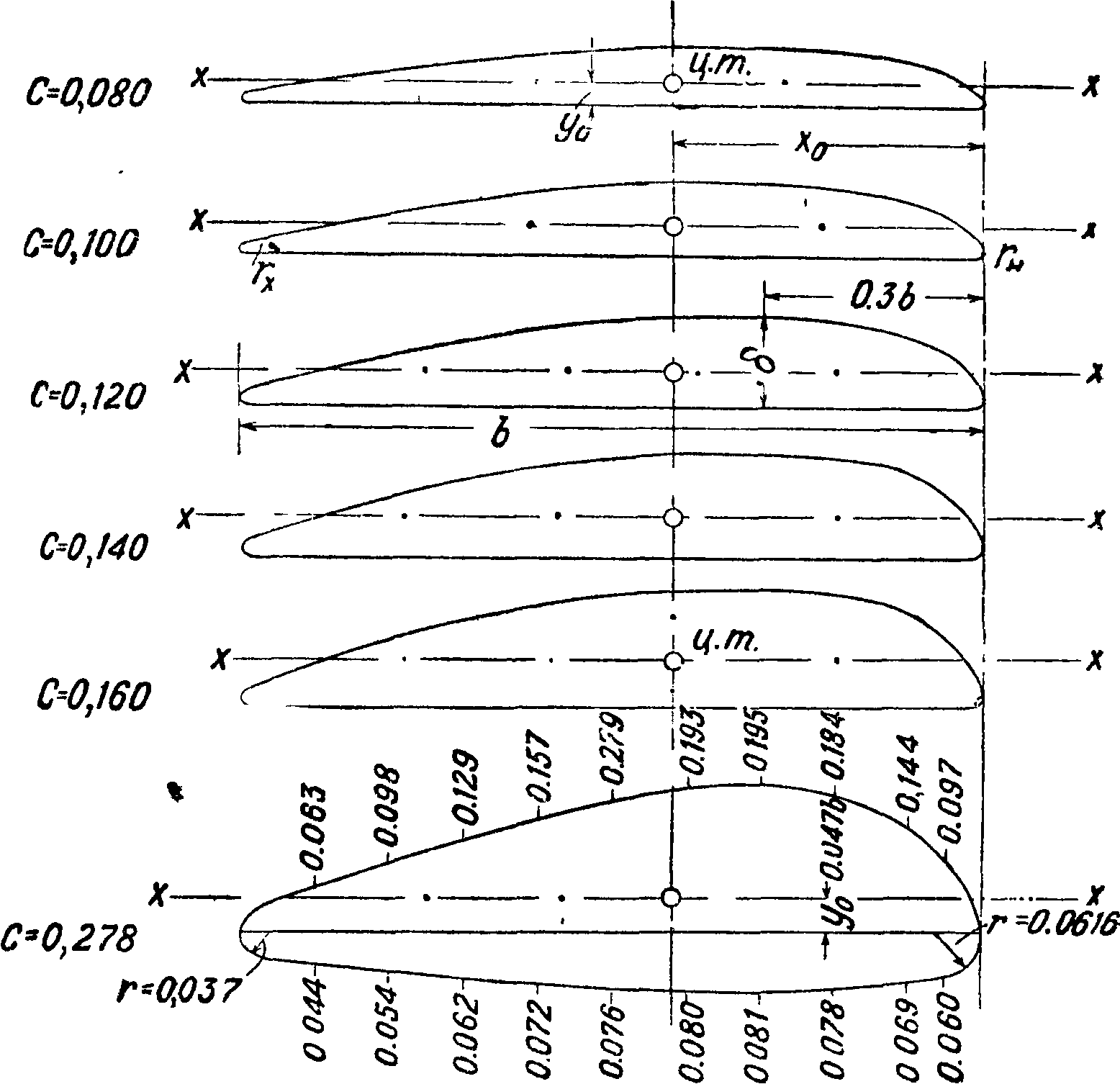
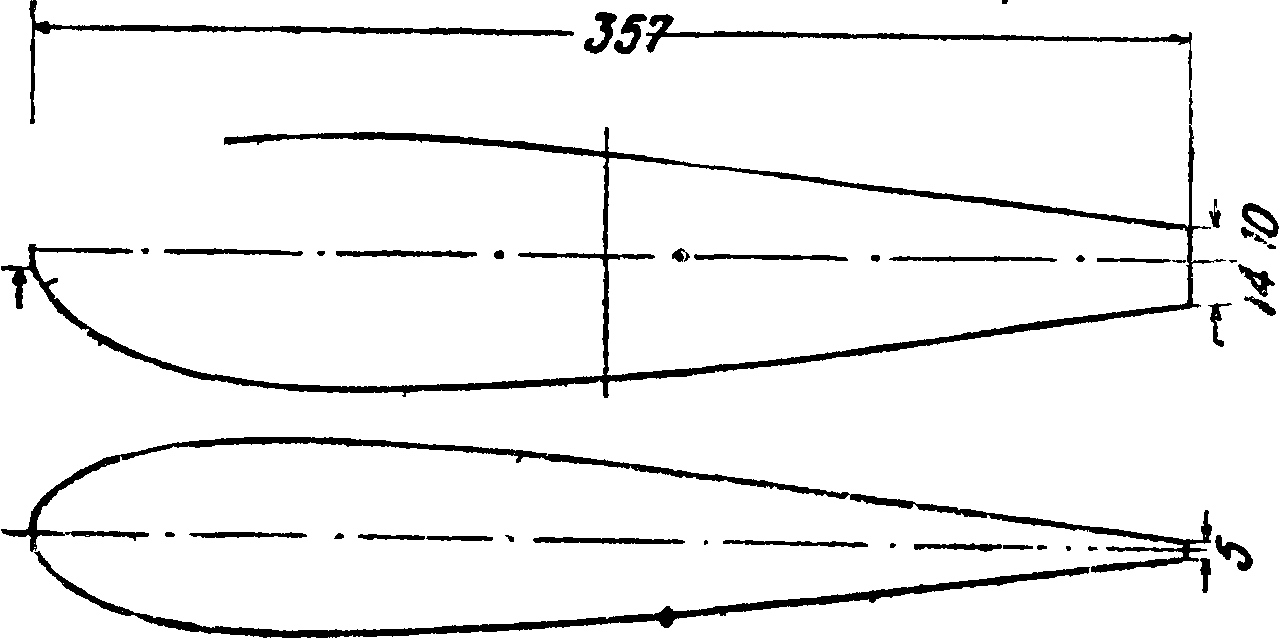
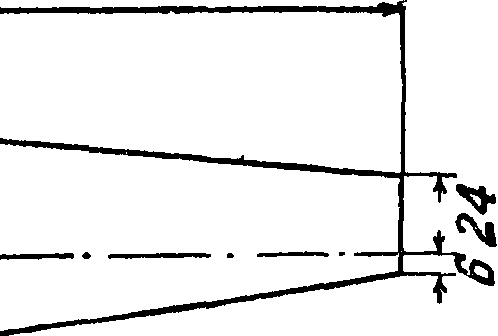
6[,w] — хорда крыла (фигура 4). За хорду крыла принимают или линию, касательную к нижней поверхности профиля крыла (касательная хорда), или линию, соединяющую носик и хвостик профиля крыла (внутренняя хорда).

11 ь] — размах крыла, — наибольший габаритный размер между концами крыльев.

s — расстояние г ентра давления (то есть точки пересечения аэродинамич. равнодействующей с хордой крыла) от носика крыла.

Q I кг) —сила лобового сопротивления,— проекция аэродинамич. равнодействующей на ось х.

4

Т· Э. Доп. т.

Р[кг]—подъемная сила,— проекция аэродинамической равнодействующей на ось у.

Т [кг]— боковая сила, — проекция аэродинамической равнодействующей на ось z.

М_х [кг“м] — момент крена, — момент аэродинамической равнодействующей относительно оси х.

М_у Iкг - м] — момент рысканья, — момент аэродинамической равнодействующей относительно оси у.

M_z [кг· м] — момент тангажа, — момент аэроди-намич. равнодействующей относительно 2.

S [м² — условная площадь, к которой относят значения аэро-динамич. сил и моментов при вычислении безразмерных коэф-тов. Для крыла за S принимают площадь его проекции на плоскость, проходящую через его центральную хорду перпендикулярно к плоскости симметрии. Для шара S равно площади его большого круга. Для дирижабля и других обтекаемых тел за S принимают площадь их миделевого сечения. Для цилиндров и стоек силы, действующие на единицу их длины, относят к площади поперечного сечения.

L м]—условная длина, к которой относят значения аэродинамич. моментов при вычислении безразмерных коэф-тов. При вычислении коэф-та момента тангажа за длину L для крыла берут его хорду b, а для самолета — расстояние между его и. т. и шарнирами руля высоты. При вычислении момента рыскания за L принимают расстояние между центром тяжести самолета и шарнирами руля направления. При вычислении момента крена за L принимают размах крыла I.

λ— удлинение крыла. Для крыла произвольной формы в плане×= l²,S, для прямоугольного крыла λ — 1/b.

С_х=— безразмерный или абсолютный коэф. лобового сопротивления.

С_у — — безразмерный или абсолютный коэф. подъемной силы. т

C_z=——безразмерный или абсолютный коэф. боковой силы.

С_тх=— безразмерный или абсолютный коэф. момента крена.

С_шу=— безразмерный или абсолютный коэф. момента рысканья.

C_mz=-gjf_L — безразмерный или абсолютный коэф. момента тангажа.

К — С_уС_х — аэродинамич. качество.

К_тах—максимальное качество.

С_{х min} — минимальное значение коэф-та лобового сопротивления.

Сушах—максимальное значение коэф-та подъемной силы.

C_Wq—значение коэф-та продольного момента для крыла при С_у=0.

Re=— число Рейнольдса. За характери-

стич. длину V для крыла берут хорду b, для шара — его диам. d.

Ва — vjc — число Бэрстоу, — отношение скорости потока к скорости звука.

Отличие принятых в СССР безразмерных коэф-тов от коэф-тов, принятых в других странах, видно из табл. 1.

Табл 1.—Безразмерные коэфициенты.

Группа	Страна	Коэф-ты лобового сопротивления		Коэф-ты подъемной силы
I	СССР. Англия. США (т. н. инженерные поэ-фициенты).	Ст hj) Кх	II Ό йИ	kl ^ Р I “ ei2s Ы 1
II	США (т. н. абсолютные коэф-ты) Германия. Франция, Япония и Бельгия. Польша.	Сп C-W СХ сх	Q	С Л са 1 Р
			~r*s	«Г*"
III	Германия. Польша.	Cw] 100 Q cj ψ- · s		Са ЮО Р [ ~ QV2 о Су) 2

III. Закон подобия. Теоретически и экспериментально установлено, что аэродинамические коэф-ты различных тел зависят от формы тела, от его положения относительно набегающего потока и от ряда безразмерных параметров. Если можно пренебрегать весом среды, что при обтекании тел воздухом или каким-либо другим газом вполне допустимо, то основными безразмерными параметрами являются следующие: 1) число Рейнольдса где V — скорость, I — линейный размер тела, V — кинематический коэф. вязкости; 2) число Бэрстоу

Ва — —,

с ⁷

где с — скорость распространения звука в данной среде, и 3) начальная турбулентность потока в аэродинамич. трубе. За параметр турбулентности потока большинством авторов принимается отношение _ Ϋ~Κν&

V

Числителем этого отношения является среднее квадратичное уклонение по времени мгновенной скорости в данной точке от средней скорости, знаменатель равен средней скорости. В ядре

Фигура 4.

течения величина τ практически постоянна по всему поперечному сечению его, дишь вблизи стенок аэродинамич. трубы имеет место нарушение ее постоянства f¹]. Т. о. C_x=f^ (форма тела, положение тела, Re, Ва, τ), C_y — f₂(форма тела, положение тела, Re, Ва, τ) и т. д. Отсюда следует, что в общем случае для равенства аэродинамич. коэф-тов двух геометрически подобных тел, помещенных в одинаковые положения по отношению к набегающему на них потоку, необходимо равенство чисел Re, Ва и т, то есть

vi · h п

V2 · h.

V2

И τ_χ=τ₂

v₂ Cl C₂

В частных случаях при Ва< 0;5 необходимо бывает удовлетворять только первому и третьему требованию, так как в указанной области аэродинамич. коэф-ты практически не зависят от чи-сда Бэрстоу. К сожалению при испытаниях моделей в аэродинамич. трубах как первое, так и третье требование в большинстве случаев не соблюдается, что приводит к расхождениям между аэродинамич. данными модели и натуры. В особо неблагоприятных случаях эти расхождения могут достигать 20—30%, а иногда и больше.

IV. Трение жидкости и воздуха о плоскую пластинку. При обтекании плоской пластинки потоком, двигающимся со скоростью v₀, вблизи пластинки вследствие трения образуется тонкий слой, внутри которого скорость V < v₀. Этот слой носит название пограничного слоя. Строго говоря, пограничный слой должен простираться до бесконечности, однако в действительности уже на небольшом расстоянии от пластинки, Которое называется высотой пограничного слоя <5, скорость частиц, находящихся внутри слоя потока, достигает скорости ν₀ внешнего потока. Внутри пограничного слоя проявляются силы вязкости, вне его поток можно считать потенциальным. Зная закон распределения скоростей внутри пограничного слоя, можно подсчитать напряжение трения по формуле:

^т°=I* ©_п=0 ^кг/мК

Различают два вида пограничного слоя: 1) ламинарный пограничный слой и 2) турбулентный пограничный слой. При ламинарном пограничном слое частицы, находящиеся внутри него, двигаются параллельно поверхности, при турбулентном пограничном слое имеет место дополнительное поперечное движение частиц, сопровождающееся переносом импульсов. При турбулентном пограничном слое можно говорить лишь о распределении средних скоростей. На фигуре 5, А приведено распределение скоростей

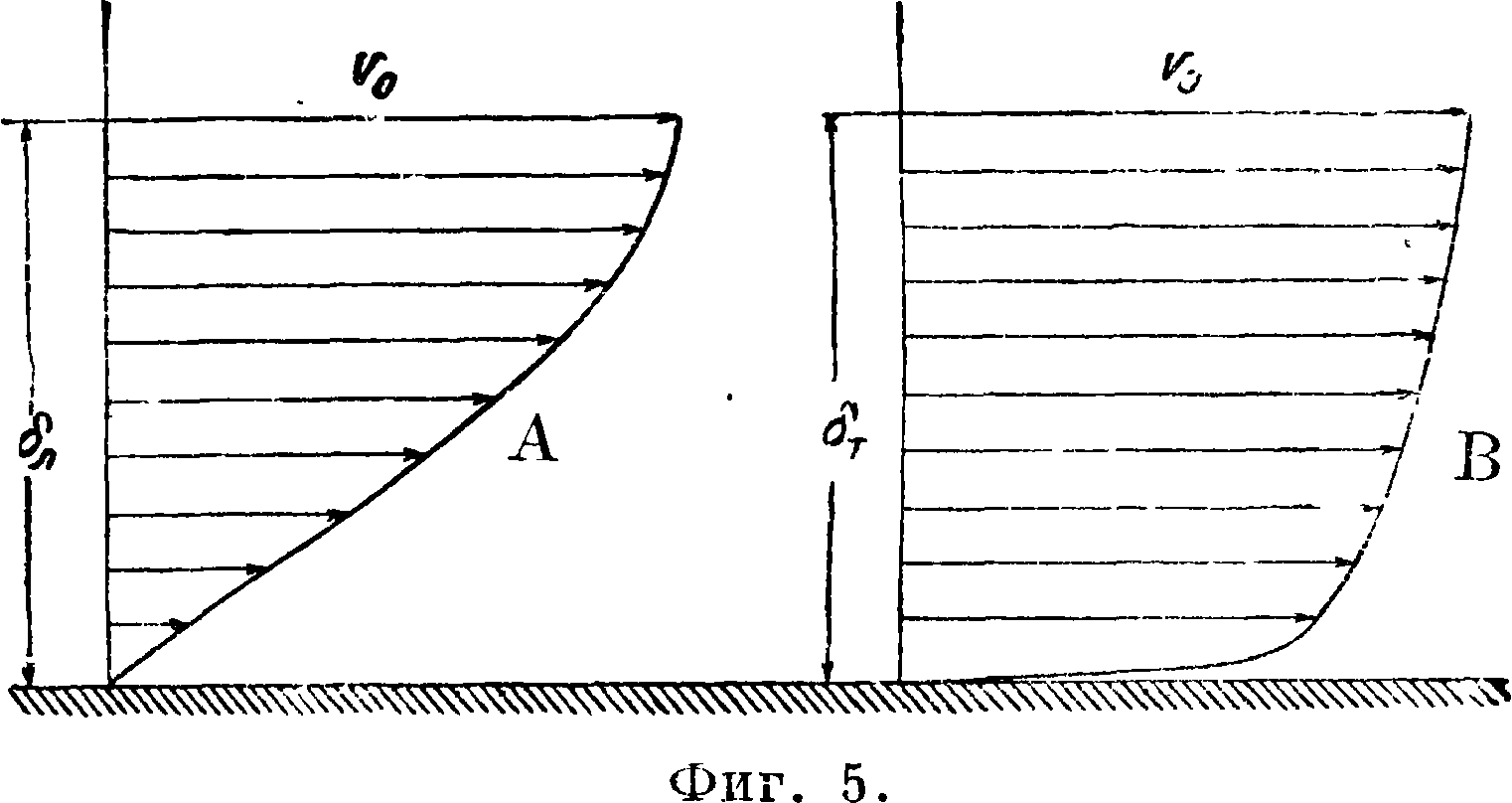
внутри ламинарного пограничного слоя, а на фигуре 5, В турбулентного пограничного слоя. При турбулентном пограничном слое в непосредственной близости к поверхности имеется тонкий ламинарный подслой. Если поместить начало коор динат в носике пластинки, а ось· х направить вдоль нее, то высота ламинарного пограничного слоя м. б. найдена по формуле Блазиуса:

где

Я

_ VQ · X

Высота турбулентного пограничного слоя в предположении, что вся пластинка покрыта им, м. б. подсчитана по формуле Прандтля и Кармана: δ_Τ=0,37 · х Л—·

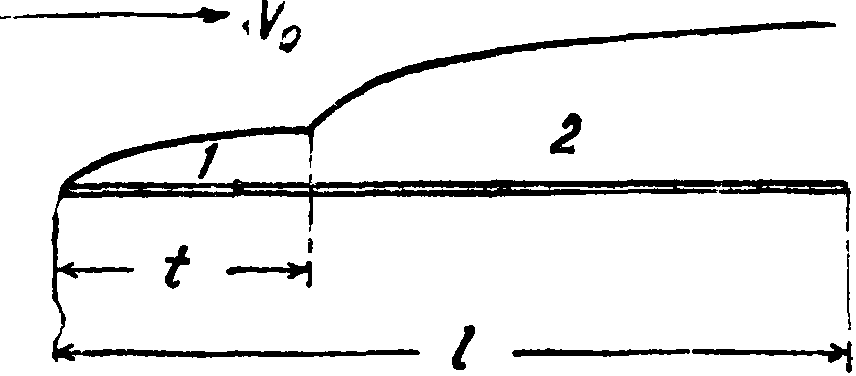
При обтекании пластинки ламинарный пограничный слой на некотором расстоянии t он переходит в турбулентный слой 2. Расстояние г м. б. определено по формуле

YRx

сначала образуется 1 (фигура 6) и лишь

Безразмерное число Фигура 6.

R_t определяется опытным путем и зависит от начальной турбулентности, формы носика пластинки и шероховатости. Число R_t находится в пределах 90 000 <R_t< 10⁶. Полная сила трения о пластинку определяется по ф-ле:

Qf=c_f · Q · F · vl,

где F — полная поверхность. Значения коэф-та Су в зависимости от 1 g Re, где Re —, а I —

длина пластинки, приведены на фигуре 7. На этой

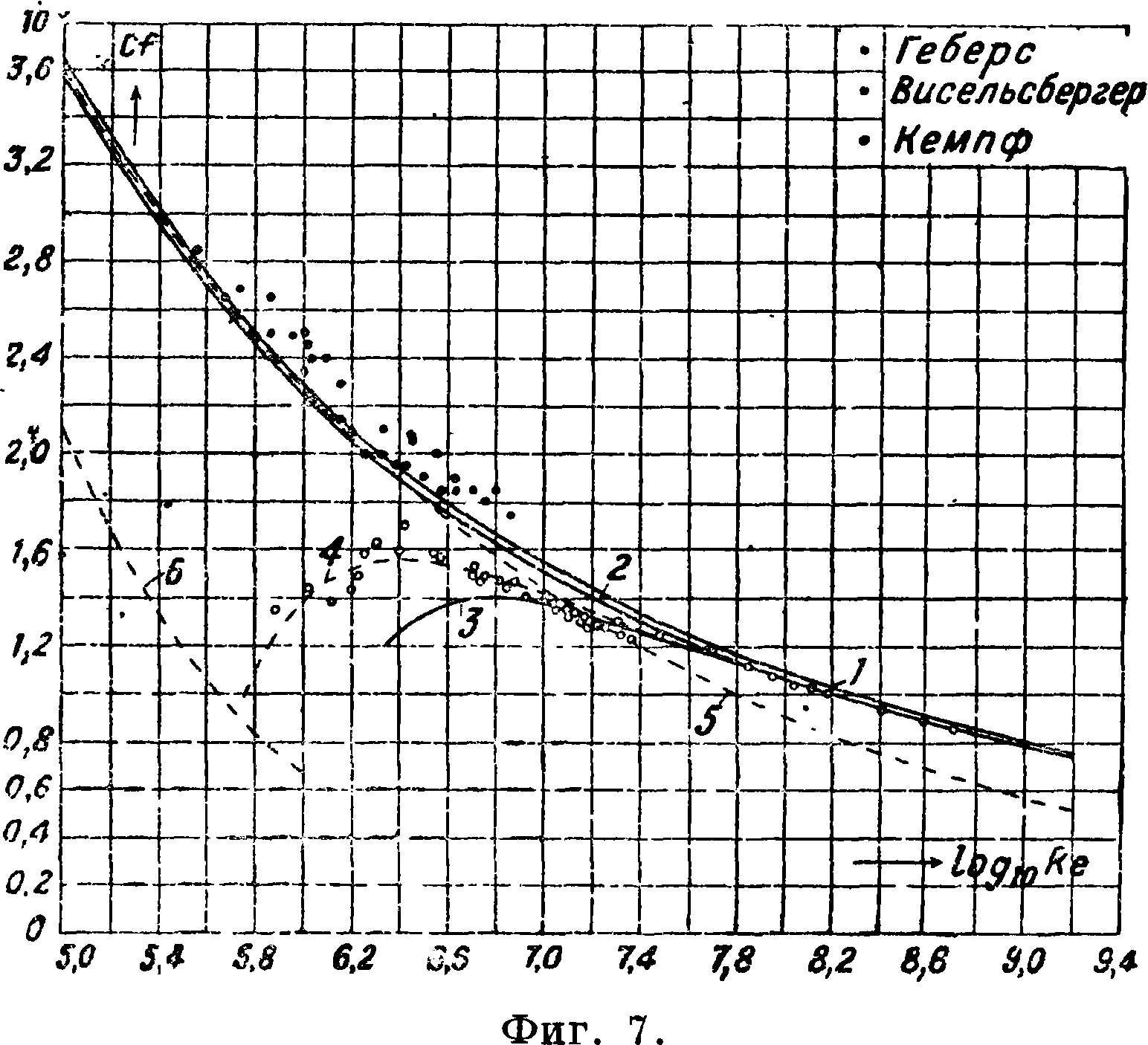
же фигуре даны и опытные точки. Кривая 6 соответствует случаю ламинарного пограничного слоя (C_f=~~ |[²]. Кривая 5 соответствует случаю чисто турбулентного пограничного слоя /Су= -f³-^²]. Более точное решение задачи [³]

V Не приводит к кривой 1, однако наилучшее совпаде-

о/п 0,2275 _гГ1

ние с опытом дает кривая 2 I ίγ=- _Дв)₂,₅₈- J ·

Промежуточному случаю, когда часть пластинки обтекается ламинарным слоем, а часть турбулентным слоем, соответствуют кривые 3 и 4 [³]. Полуэмпирич. кривая 4 дает значительно лучшее совпадение с опытами, произведенными Геберсом; соответствующая формула имеет вид у, 0,2275 850

^f ~ (lg Re)2’58 R_e *

При пользовании этой формулой следует помнить,

что она получена на основе опытов Геберса, которым для числа R_t было найдено значение Щ=485 000. При иных условиях величина C_f для промежуточного слоя может быть отлична от подсчитываемой по приведенной формуле [²,³,⁴].

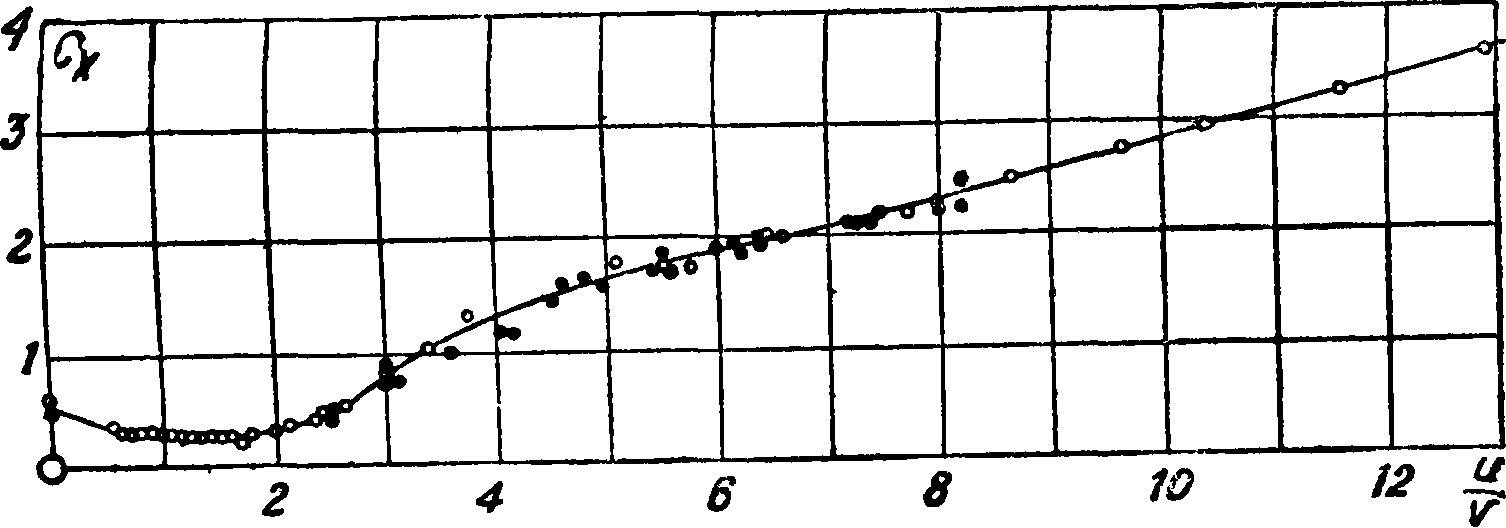
V. Лобовое сопротивление простейших тел. Полное лобовое сопротивление различных тел слагается из двух сопротивлений: 1) сопротивления трения Qf и 2) сопротивления формы Q—. Первое обусловливается грением воздуха о поверхность тела и равно

Qf — Jrо · cos δ · dF,

F

где τ₀ — напряжение трения в данной точке поверхности, а δ — угол между направлением элементарной силы трения τ₀ dF в данной точке

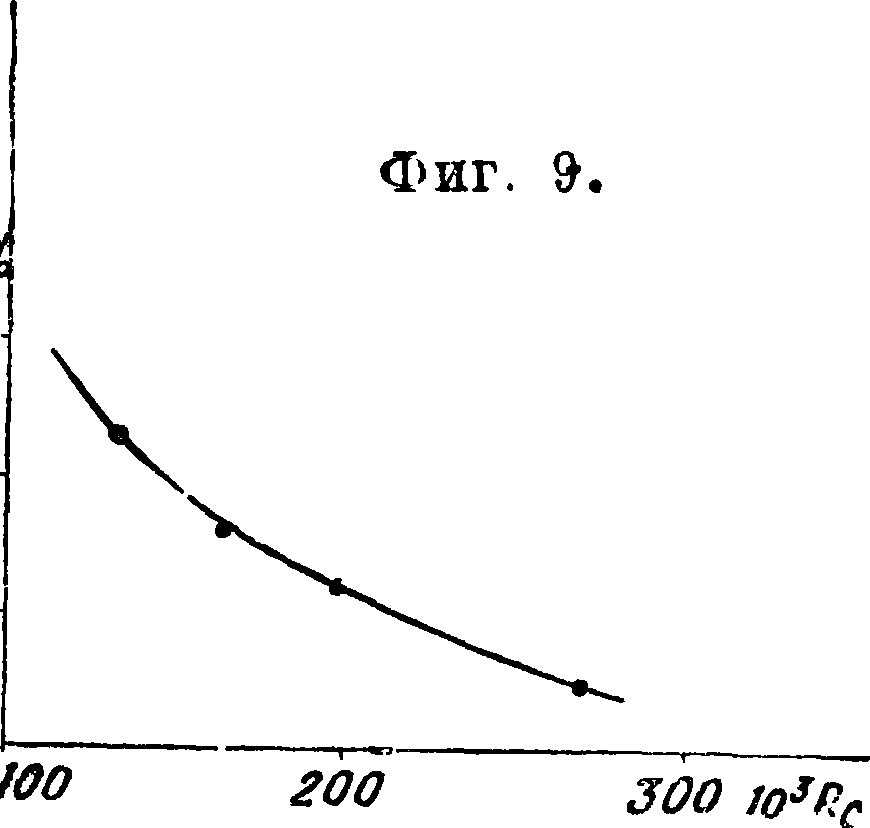
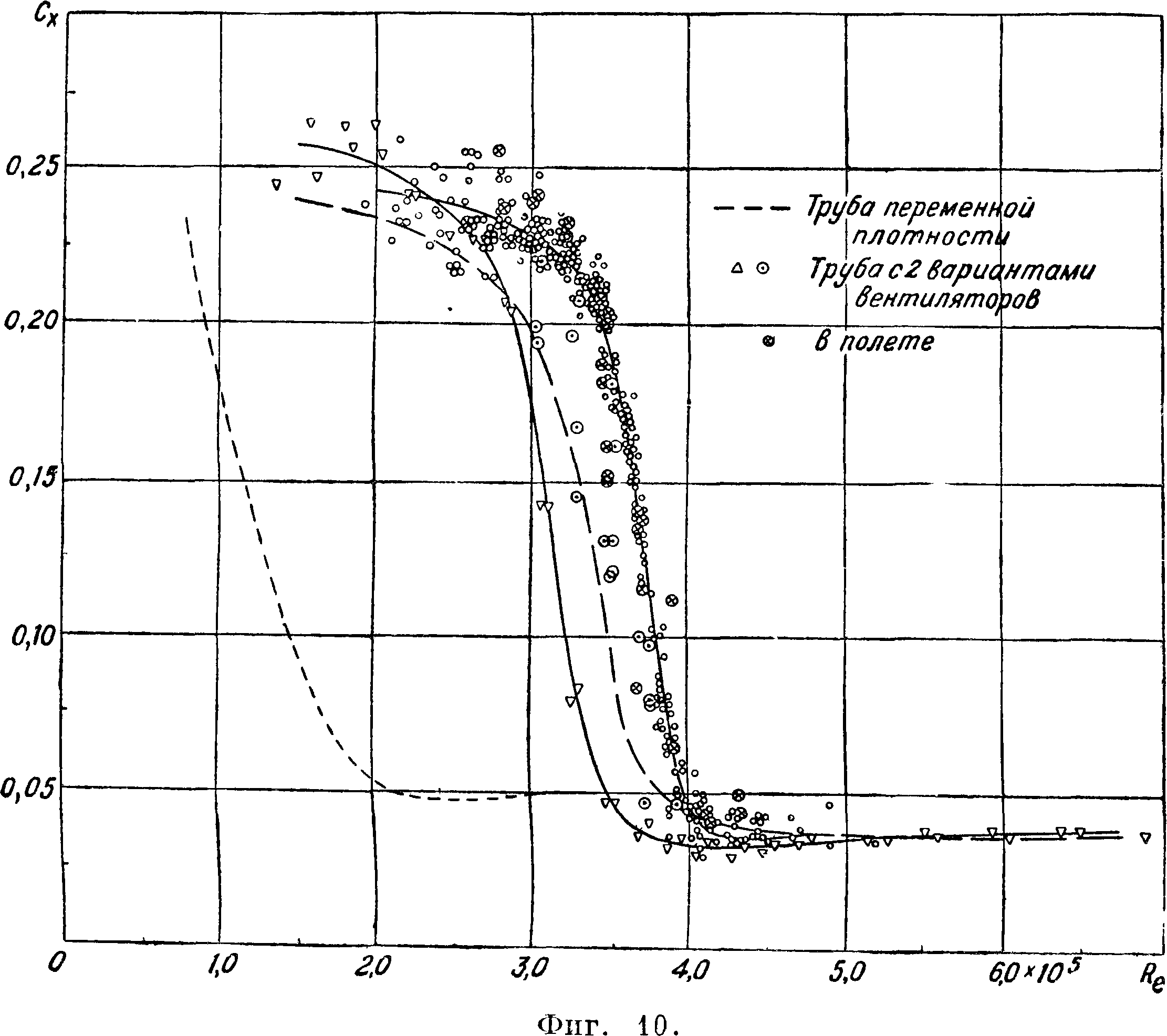
Из диаграммы видно, что кривые не совпадают, это явление объясняется различиями в степени начальной турбулентности в различных трубах. Кроме того видно, что в известной области чисел Рейнольдса наступает весьма резкое уменьшение коэф-та сопротивления. Это явление носит название «кризиса». Диаграмма показывает, что кризис наступает в различных трубах при различных числах Рейнольдса. Было установлено, что чем больше начальная турбулентность, тем при меньших числах Рейнольдса наступает кризис, поэтому кривая С_х шара может до некоторой степени служить для количественного определения степени турбулентности. По предложению Драйдена за критическое числоРей-нольдса R_c для шара принимается число Рейнольдса при 0^= 0,15 [⁶]. На фигуре 9 приведена связь между числом R_c и т, найденная Драйденом и Куэттом [⁶]. Числа R_c, приведен-

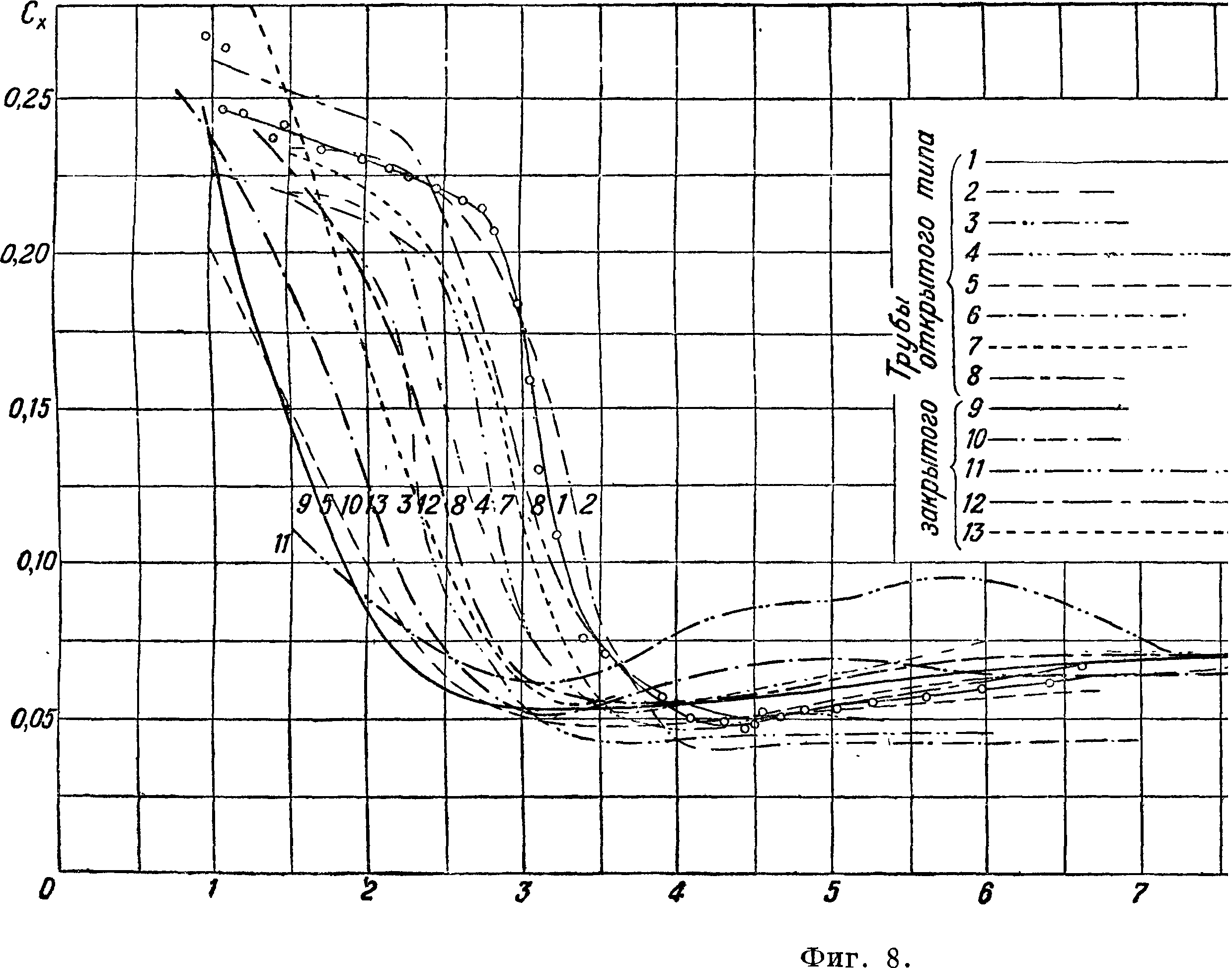
Труба о

ЦАГИ Т-V 2£5м

---Геттинген 2β6«

----- « 7,5 "

" 1,2 «

В.ВЛТ.-И 15"

- Аахен 1,85"

Фрадрихсгарен 2j9

---- Харьков Т-II

ЦАГИ Т-1 3,0"

--Рим 16"

" 2,0

В. В. А Т-Т 2,25

Харьков TI 1,2 м

/О 10%

и направлением потока вдали от тела (направлением полета); интеграл берется по всей поверхности тела. Сопротивление формы равно

Qp=Р cos γ · dF,

F

где p равно разности давлений между давлением в данной точке тела и статич. давлением в потоке, а γ — угол между нормалью к поверхности в рассматриваемой точке и направлением потока. На аэродинамических весах (смотрите) определяется всегда полное лобовое сопротивление. Сопротивление трения м. б. найдено как разность между полным сопротивлением и сопротивлением формы. Последнее легко определяется графич. интегрированием нормальных давлений, найденных опытным путем. На фигуре 8 приведена диаграмма испытания гладкого алюминиевого шара е?=0,242 метров ЭАО ЦАГИ в различных аэро-динамич. трубах [⁵]. По оси ординат отложен коэфициент С_х=—~— лобового сопротивле-* ‘^v2

ния, а по оси абсцисс число Рейнольдса Re=—

V ·

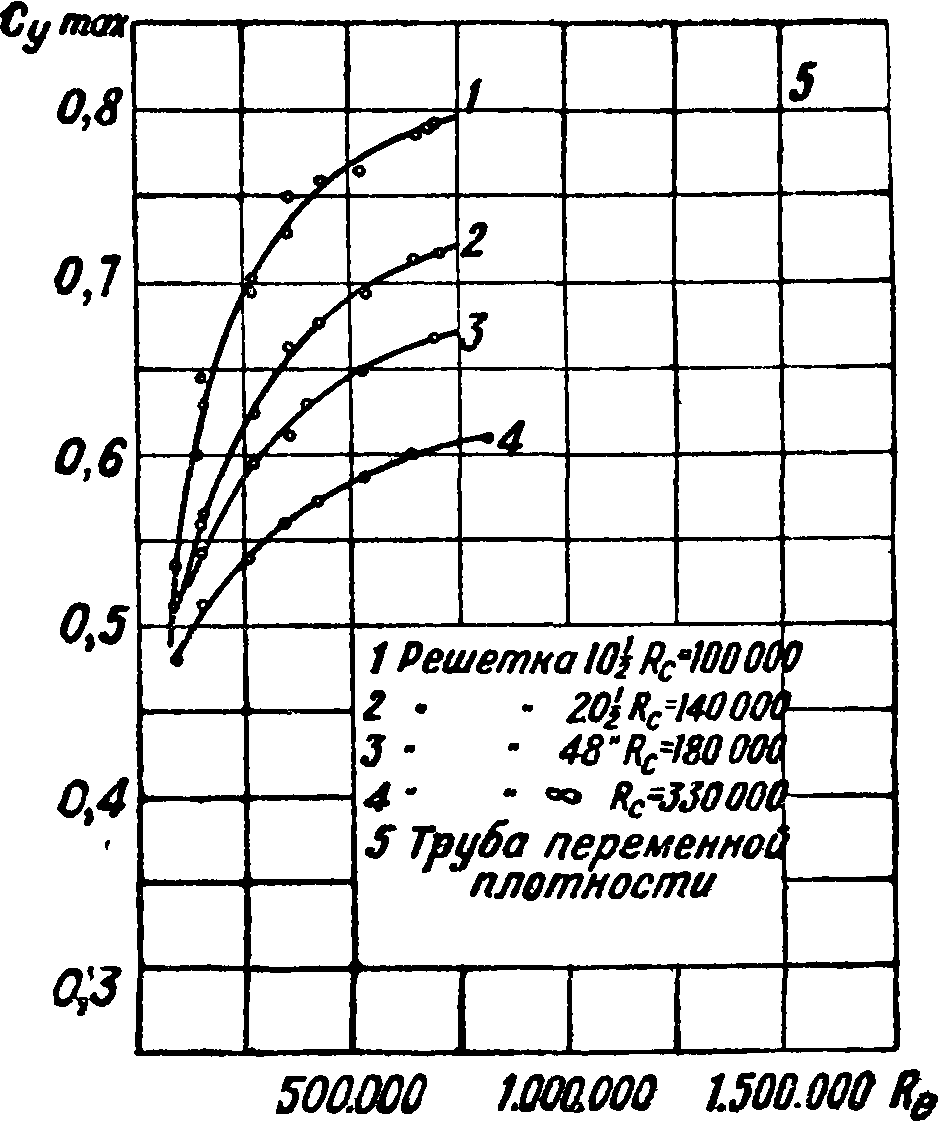
ные на диаграмме, получены как средние из критич. чисел для шаров различных диаметров, а именно d=0,1014, 0,127 и 0,218 метров Позднее (по испытаниям в одной трубе) Милликен и Клейн [⁷] обнаружили слабо выраженную зависимость R_c от диаметра шара.

На фигуре 10 приведены результаты испытания шара d=0,2 метров в трубе т переменной плот- j

ности в ее третьем варианте, шара d=г

= 0,1143 метров в трубе Калифорнийс-

кого технологического института с о двумя вариантами вентиляторов и шара d == 0,15 метров в полете [⁷]. Диаграмма показывает весьма значительную начальную турбулентность потока в трубе переменной плотности (R_c=117 000) и," наобо рот, чрезвычайно ничтожную турбулентность воздуха в условиях полета (R_c=365 000).

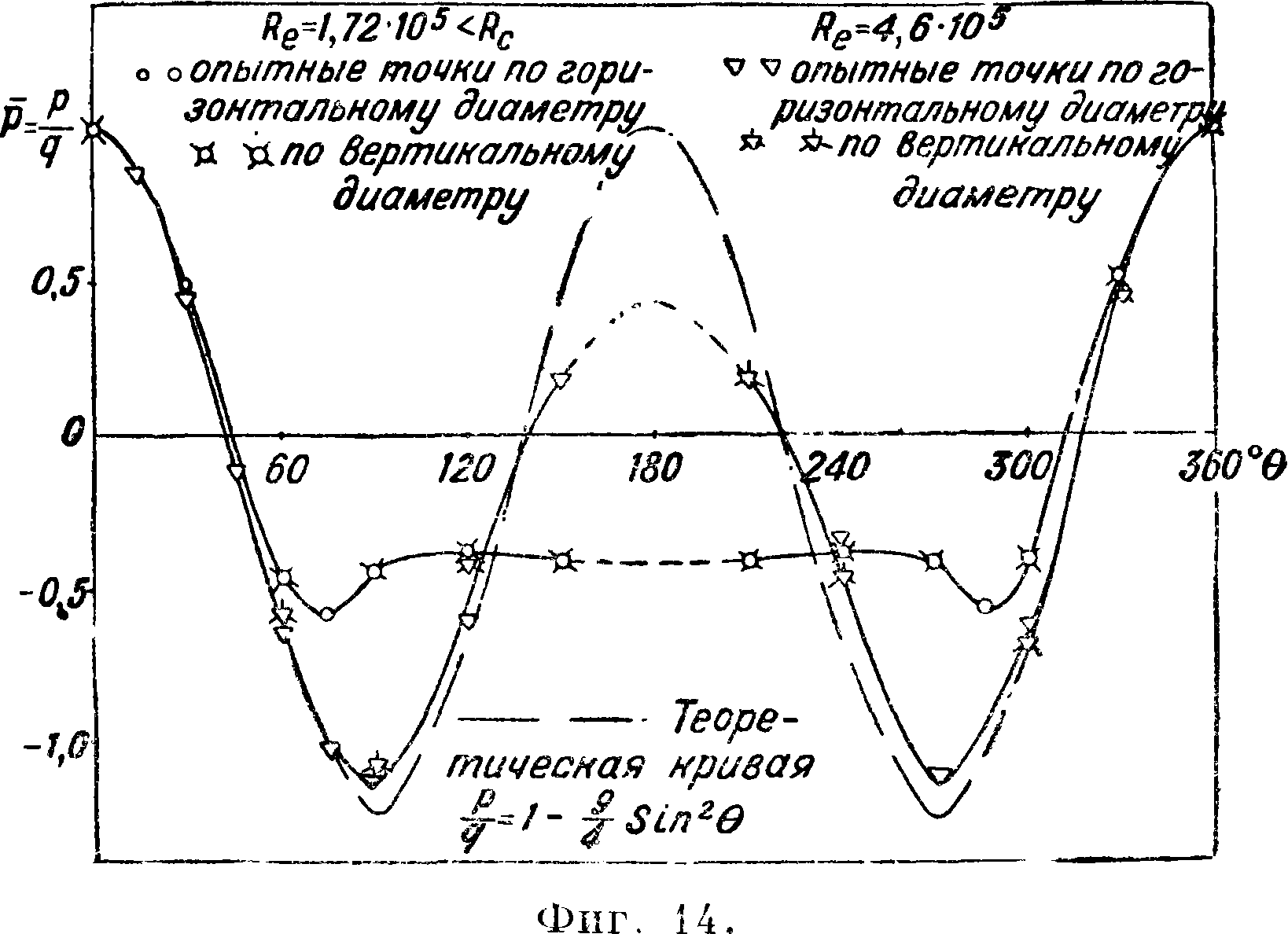
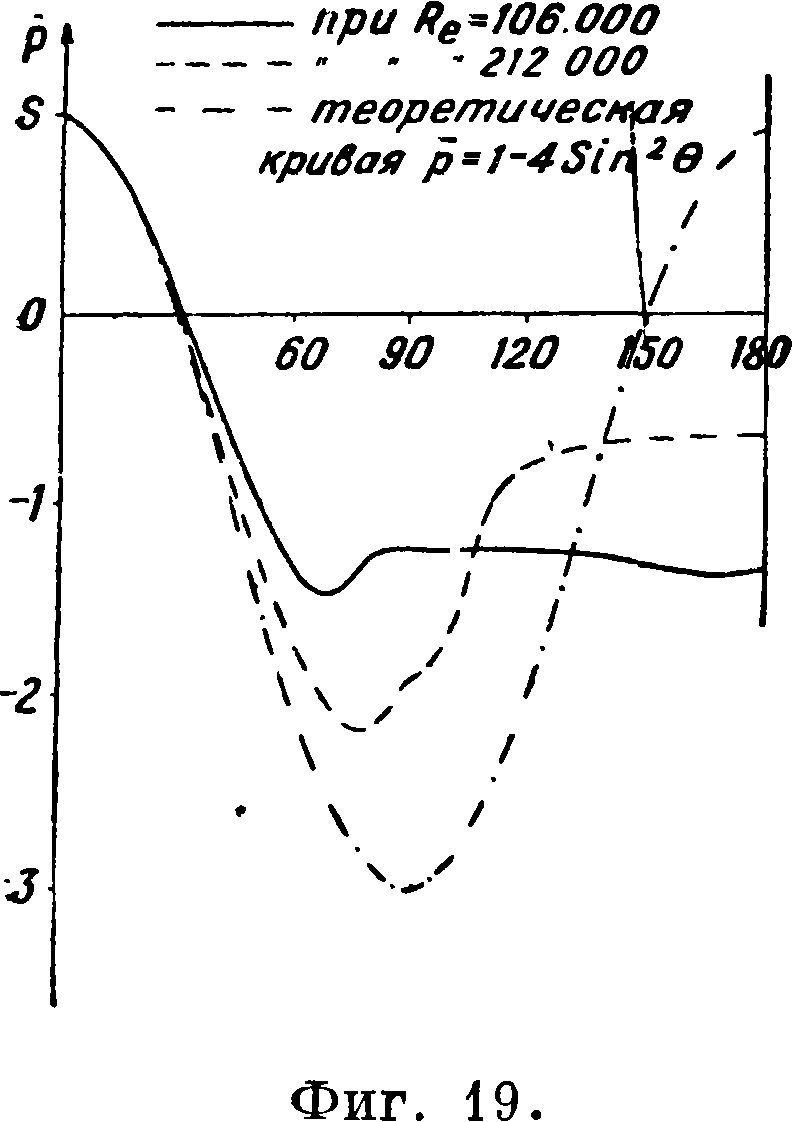
Явление кризиса замечательно еще тем, что не только в несколько раз уменьшается коэф. сопротивления, но наступает даже уменьшение проволочного конца. На фигуре 14 приведено распределение давления по шару d=0,242 метров до и после кризиса [⁸]. По оси ординат отложен коэф.

давления р =, а по оси абс цисс— центральный угол. Диаграмма показывает, что до кризиса имеет место существенная разница между теоретич. распределением давления по шару, обтекаемому потоком идеальной жидкости=1 —у sin² Θ j, и действительным давлением; это вызывает большое сопротивление формы. Наоборот, после кризиса действительное распределение давления весьма близко к теоретическому, и сопротивление формы в этом случае невелико.

Лобовое сопротивление шара в вязкой жидкости было теоретически найдено Стоксом и Озееном. Ф-ла Стокса:

ф-ла Озеена:

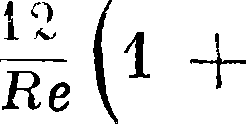
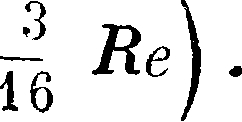
ю го jo 40

Фигура 11»

лобового сопротивления. На фигуре 11 дана зависимость Q по у для шара d=0,242 ж, испытанного в трубе T-V ЭАО ЦАГИ. Экспериментально установлено, что чем больше число Рейнольдса, тем центральный угол определяющий точку образования турбулентного пограничного слоя, боль- ₀₅ше, поэтому при малых числах Рейнольдса срыв о,4 потока с шара происходит до образования турбулент- °·³ ного пограничного слоя.

Наоборот, с увеличением ^ числа Рейнольдса насту- о,г пает момент образования турбулентного погранич- ^ ного слоя до точки срыва. Турбулентный пограничный слой по сравнению с ламинарным слоем обладает способностью проникать дальше в область нарастающего давления, и следовательно в момент образования турбулентного пограничного слоя обтекание должно улучшиться, а лобовое сопротивление должно упасть, то есть должен наступить кризис.

На фигуре 12 приведен дымовой спектр обтекания шара, полученный Висель-сбергером; снимок этот получен до кризиса. Второй снимок потока (фигура 13) получен при том же числе Рейнольдса, но после кризиса. Последний был вызван искусственно созданным турбулентным пограничным слоем, что было достигнуто укреплением на передней поверхности шара тонкого

Фигура 12.

Эти формулы дают удовлетворительное совпадение с опытом только при Re< 1, причем формула Стокса дает преуменьшенные значения, а формула Озеена — преувеличенные значения. Лобовое сопротивление шара в очень большом диапазоне чисел Рейнольдса было определено в Геттингенской аэро-динамич. лаборатории [⁹].

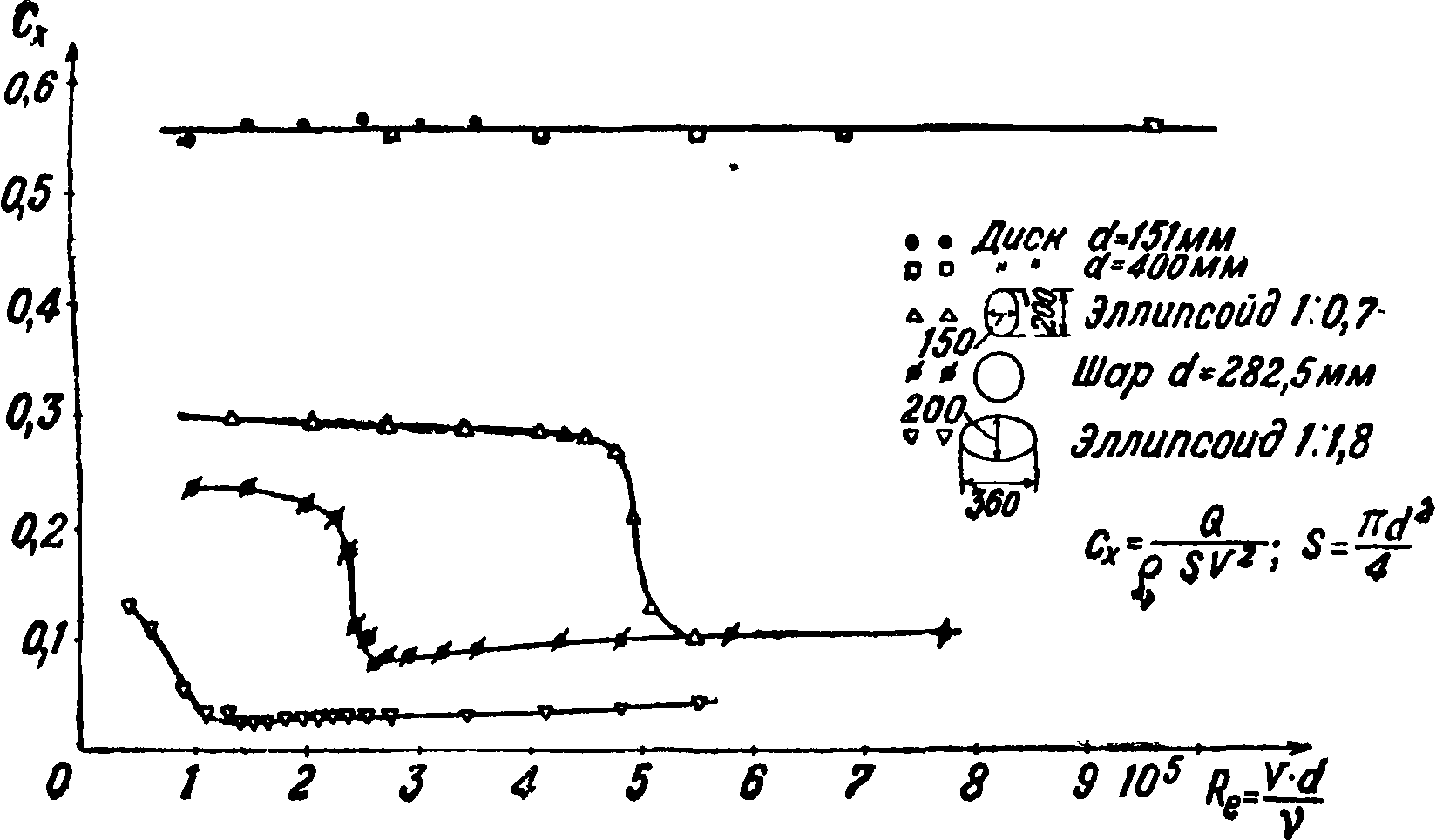
На фигуре 15 приведена зависимость коэф-та С_хот числа Рейнольдса для диска, шара и двух эллипсоидов [⁹]. Диаграмма показывает, что со

противление круглой плоской пластинки хорошо следует закону квадрата скорости, причем кризис не имеет места. Наоборот, у таких тел, как шар и эллипсоид, имеет место кризис, причем чем тело более обтекаемо, тем при меньших числах Рейнольдса наступает кризис.

На фигуре 16 дана зависимость коэфициента С_х от числа Рейнольдса для модели дирижабля (фигура 17) при различных начальных турбулентностях потока [¹⁰]. Повышенная турбулентность потока вызывалась проволочной сеткой, устанавливавшейся на различных расстояниях от модели. Степень турбулентности определялась по критич. числу Рейнольдса для шара <2=0,198 метров Диаграмма показывает на значительное воз-

кривая распределения давления для случая потока идеальной жидкости (р =1—4 sin² 0). Две опытные кривые распределения давления соответствуют двум ч Рейнольдса, равным 106 000 и 212 000. В первом случае обтекание докризис-

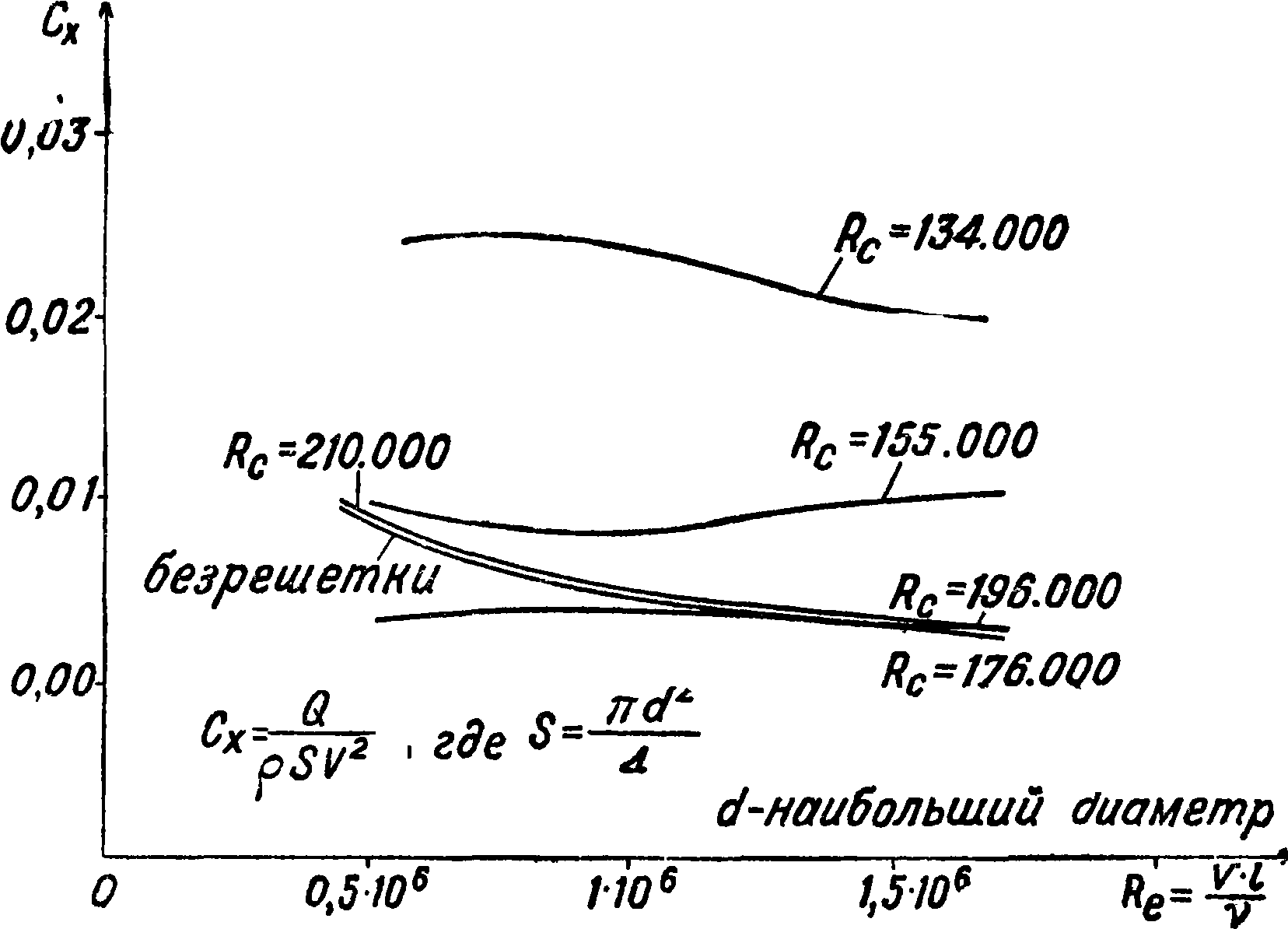
Фигура 15 и 16.

-0,391-

Фигура 17.

растание коэф-та сопротивления при увеличении турбулентности. (Кривая, соответствующая R_c —

= 176 000, повидимому 1=89мм d=17,8мм Объем 17*0,0128м“ является ошибочной.)

Это явление вызывается преждевременным образованием турбулентного пограничногослоя, при наличии которого коэфициент трения больше, чем при ламинарном пограничном слое. Так как сопротивление хорошо обтекаемых тел главным образом обусловливается трением, то понятна причина отмеченного уве-личения лобового сопротивления.

При больших числах Рейнольдса влияние начальной турбулентности будет значительно меньше.

Влиянием начальной турбулентности объясняются значительные расхождения в результатах испытаний геометрически подобных моделей дирижаблей в различных аэродинамич. трубах при одинаковых числах Рейнольдса.

На фигуре 18 приведены результаты испытаний в большой трубе (<2=2,26 м) Геттингенской аэродинамич. лаборатории круглого цилиндра при различных числах ное. Второй случай соответствует моменту окончания кризиса. Опыты не были доведены до закри-зиснрго режима; последнему в данной трубе соответствуют числа Re < 289 000. На фигуре 20 приведена зависимость коэф-та лобового сопротивления от числа Рейнольдса для двух симметричных профилей. Опыты проводились в трубе переменной плотности при двух начальных турбулентностях [¹³]. Относительная толщина профилей в процентах от хорды равнялась 6 и 21%. Повышенная турбулентность вызывалась установкой перед моделями сетки из металлических лент. Степень турбулентности определялась по критич. числу R_c для

Рейнольдса в случае и Я=5 [“]. В области

= оо

200 000<Яб<500 000 имеет место кризис, вследствие которого коэф.

С_х уменьшается в четыре раза.

Необходимо принимать во внимание, что момент наступления кризиса, как и для шара, зависит от начальной турбулентности.

Теоретич. формула Ламба для коэф-та сопротивления цилиндра, обтекаемого потоком вязкой жидкости, имеет вид:

Цилиндр Л=оо Ццлимдр λ=5 + 0.05мм Диаметр © 4. Омм Диаметр О 0.1 · " о 7 0 * 0.3 * « * 13.0 * 1.0 " 11 ° 42.0 * “ 3.0 » " · 80.0 · · * 7.9 * * * 300 * * 42.0 " ! * 80.0 " * © 30.0 · »

N

ч

Ф ч

орЩ

/Л О

La;

пЬа

N

V

+

ч

ч

>

Ik

r-Λ-β·

>r

V.

%

©Ал

j4-c

y

А=5

IA

ί

OJ

1 2 5 10

IP⁹ to·*

Фигура 18.

10⁴

10⁵

10⁶Я_Л

С=-

Ал

Re (2,002 — In Не) *

Эта формула применима лишь при очень малых числах Рейнольдса (фигура 18). На фигуре 19 дано распределение давления по круглому цилиндру <2=0,15 метров [¹²]; кроме того приведена теоретич.

шара. Ярко выраженные минимумы С_х при испытаниях без сетки соответствуют моменту образования турбулентного пограничного слоя. Величина и закономерность изменения коэф-та С_х для тонкого профиля при повышенной турбулентности в трубе находятся в хорошем соответствии с величиной и закономерностью изменения коэфициента трения при чисто турбулентном пограничном слое (фигура 7). Разница в коэфициентах сопротивления толстого и тонкого профилей обусловливается большим сопротивлением формы толстого профиля.

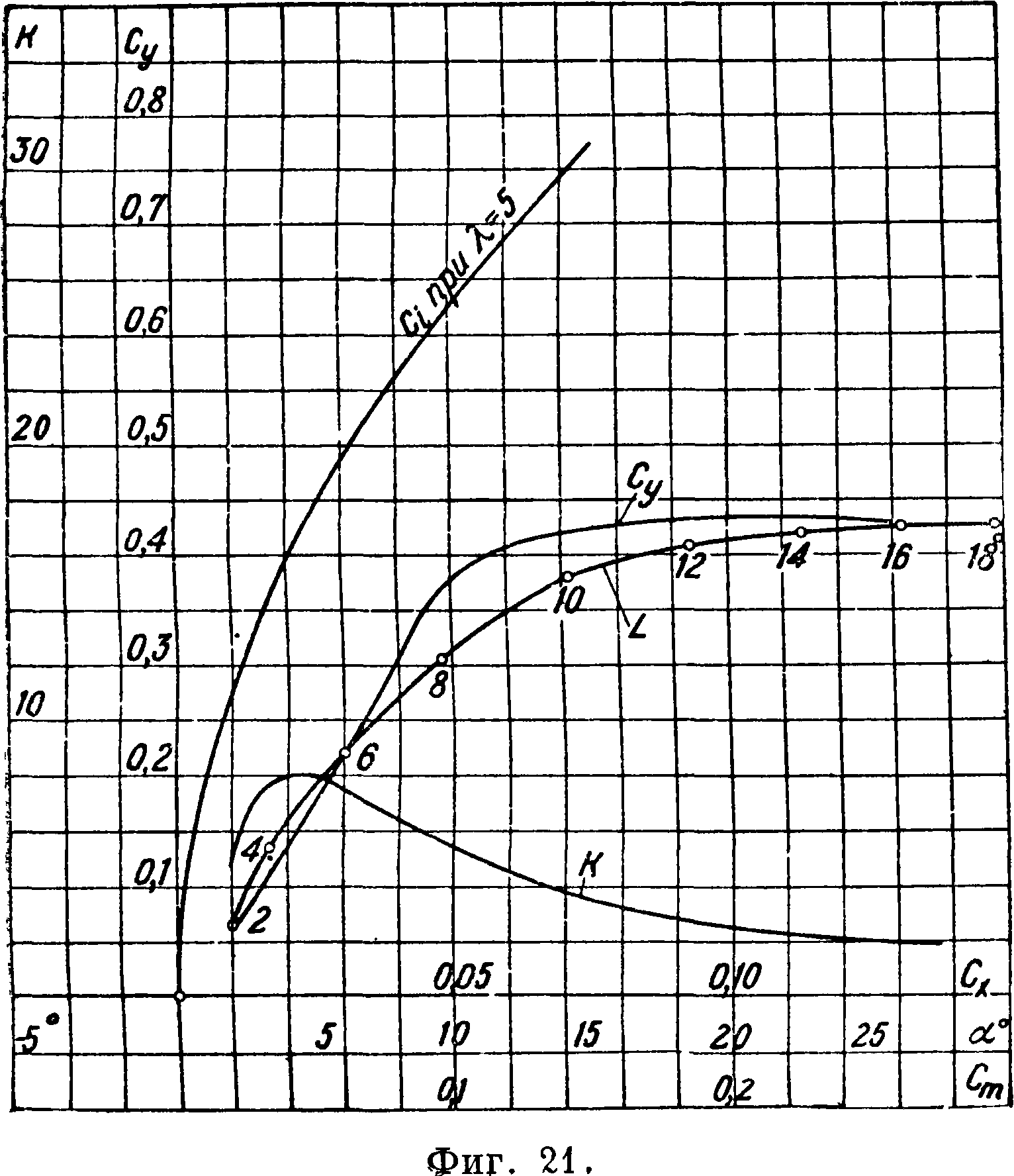
VI. Аэродинамические характеристики крыльев. Простейшим крылом является плоская пластинка. На фиг, 21 приведены результаты испытания плоской пластинки на С_у и С_х f¹¹]. На диаграмме дана кривая С_у по а, поляра Лилиенталя L и кривая каче-

л ства/f—^ по а. Крылья

ЬX

в виде плоских пластинок в настоящее время не употребляются вследствие низкого С_{у тах} и большого профильного сопротивления. Значительно

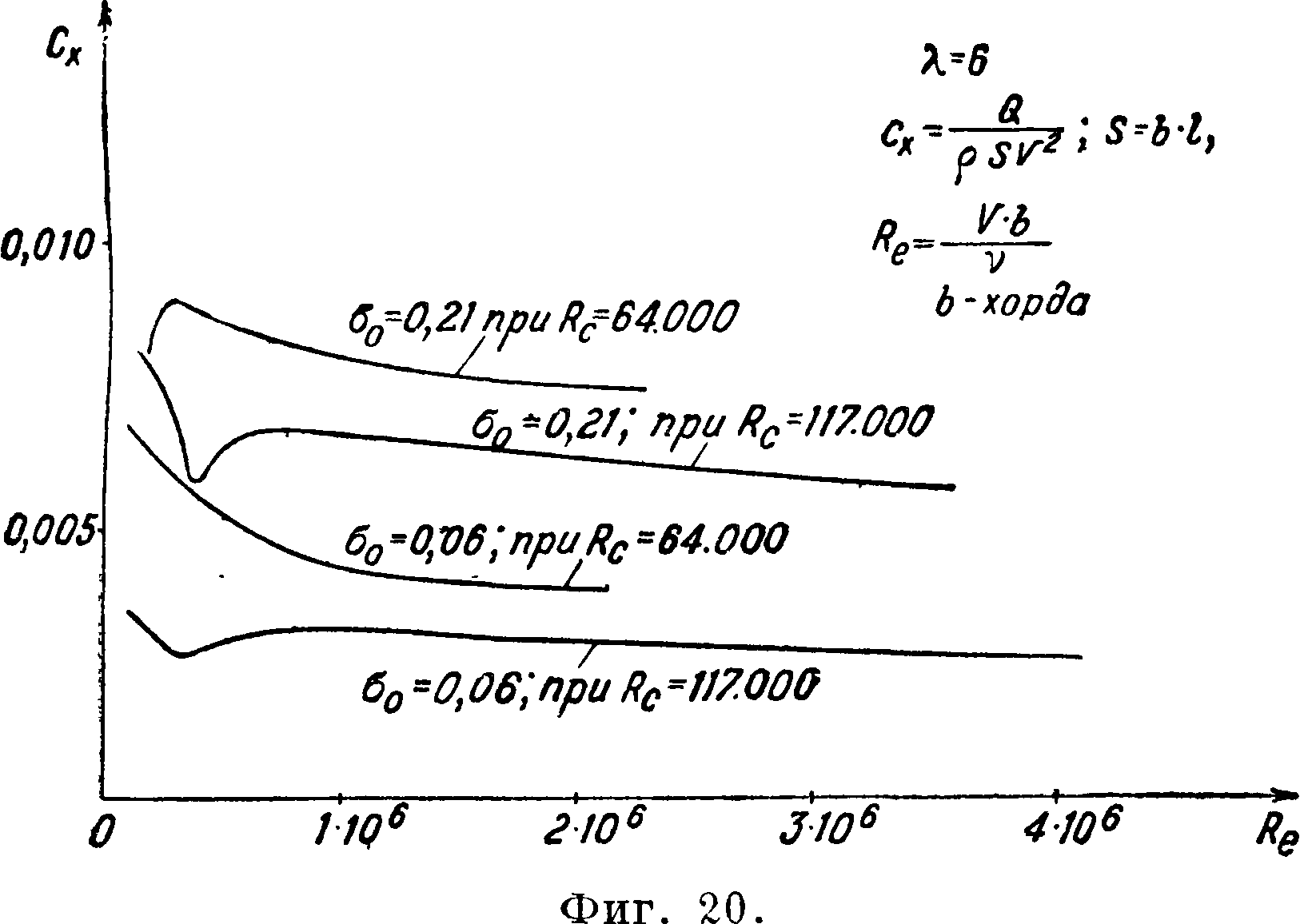
ные незакрученные крылья стандартных удлинений. В Союзе ССР, Германии, Франции и Польше принято удлинение Я=5, а в США и Англии Я=6.

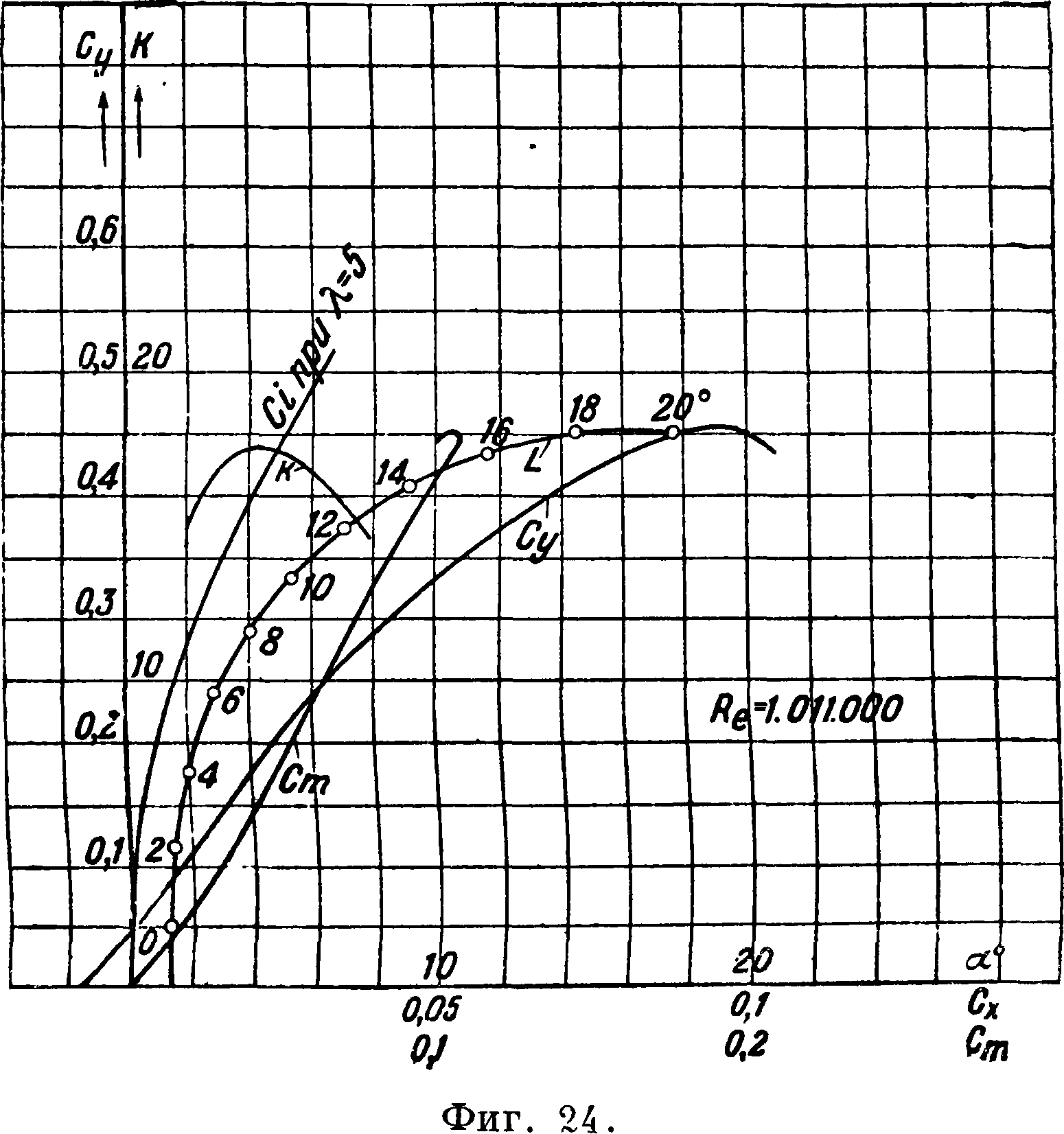
На фигуре 22, 23 и 24 приведены результаты испытания в трубе Т-I ЦАГИ трех прямоугольных крыльев, а в таблице 2 и 3 даны координаты их про

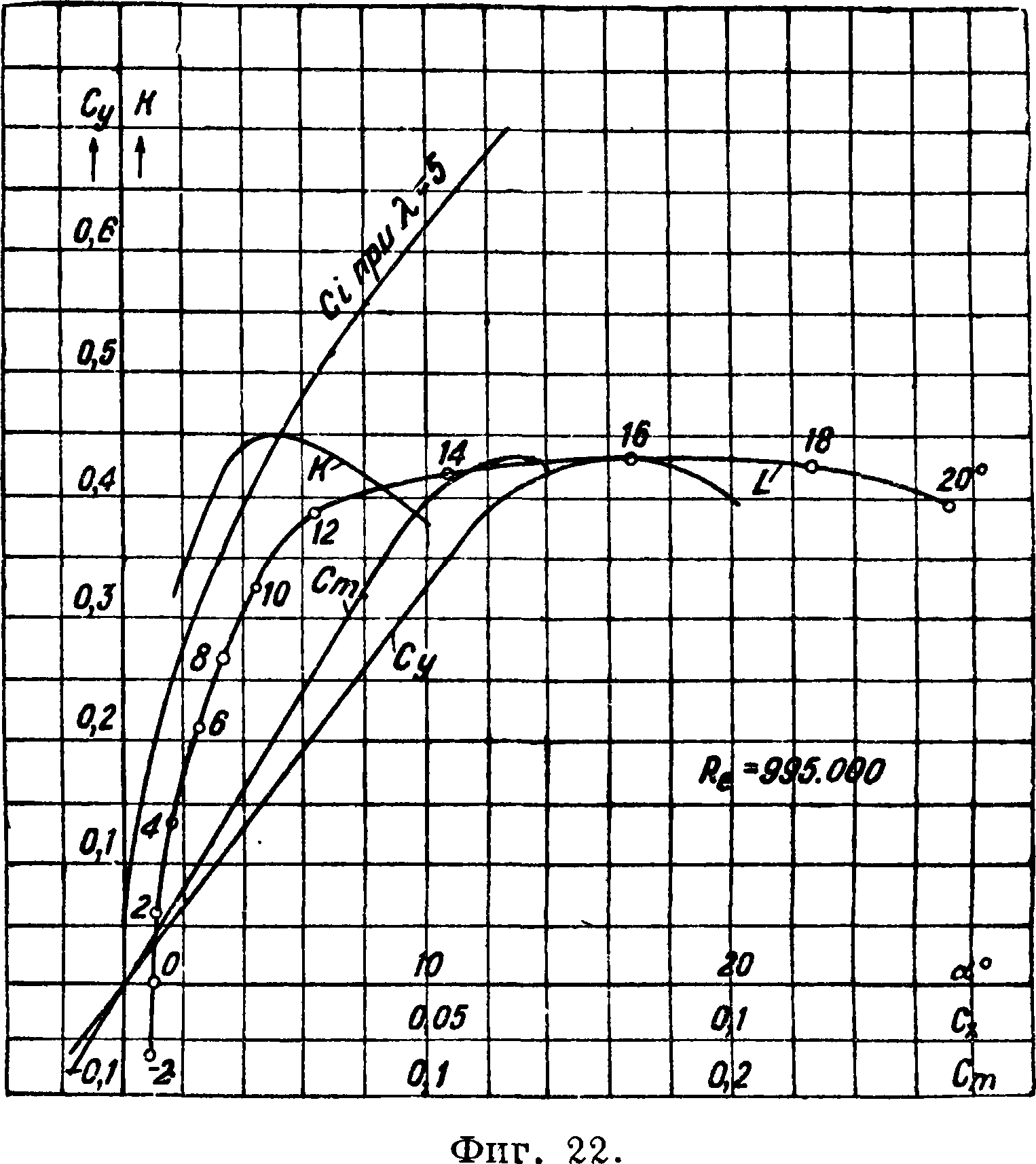
филей в процентах от хорды и аэродинамич. коэф-ты. Симметричные профили (фигура 22) характеризуются малым минимальным профильным сопротивлением, малым С_утах и постоянным центром давления. Крылья с симметричным профилем встречаются очень редко; симметричные профи-

выгоднее придавать профилю крыла обтекаемую форму. Аэродинамич. характеристики крыла во

многом зависят от формы его профиля. Для определения аэродинамических свойств профиля в аэродинамич. трубах испытываются прямоуголь

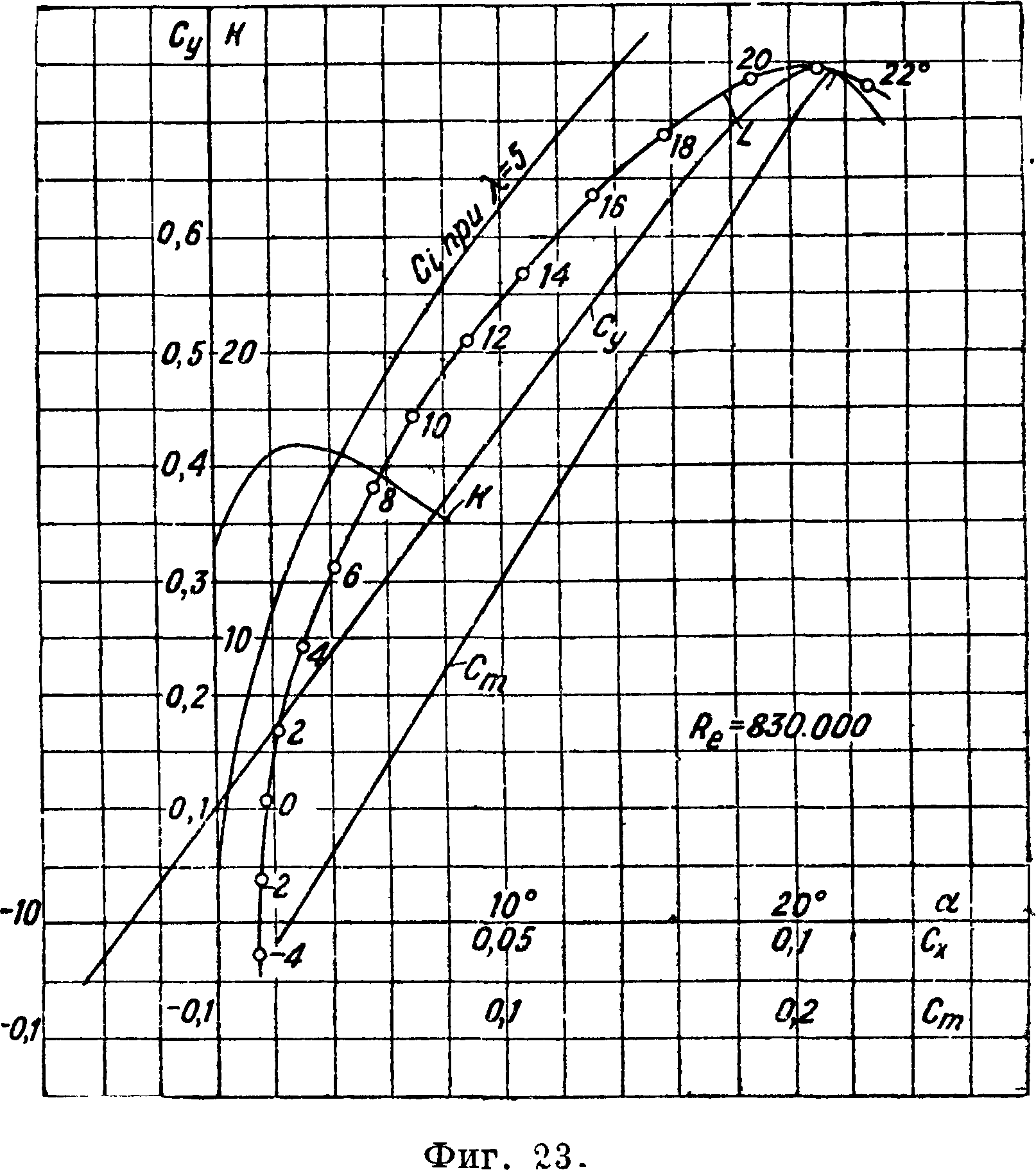
ли употребляются гл. обр. для горизонтального и вертикального оперения самолетов. Профили крыльев почти всех самолетов несимметричные. Результаты испытаний одного из таких профилей приведены на фигуре 23. На фигуре 24 даны резуль_ттаты испытания профиля В—S с острой передней

Профиль RAF-30
X	0.00	1,25	2,5	5,0	7,5	10	15	20	30	40	50	60	70	80	90	95	100
Ув	0,00	1,40	1,96	2,74	3,28	3,70	4,30	4,70	5,00	4,90.	4,47	3,78	2,91	1,98	1,03	0,54	0,00
Ун	0,00	1,40	1,96	2,74	3,28	3,70	4,30	4,70	5,00	4,90	4,47	3,78	2,91	1,98	1,03	0,54	0,00
Профиль Р-П-16
X	0,00	1,25	2,5	5,0	7,5	10	15	20	30	40	50	60	70	80	90	95	100
Ув	0,00	3,26	4,7	6,77	8,25	9,40	10,92	11,75	11,94	11,28	10,02	8,34	6,45	4,43	2,27	1,13	0,00
Ун	0,00	-1,77	-2,42	-3,02	-3,33	-3,64	-3,78	-3,93	—4,00	-3,77	-3,30	-2,77	-2,15	-1,46	-0,76	-0,39	0,00
1 Профиль B-S-16
I ! х !	0,00	1,25	2,5	5,0	7,5	10	15	20	30	40	10	60	70	80	> 90	95	100
Ув	0,00	1,36	2,50	4,35	5,75	6,87	8,65	9,80	10,71	10,40	9,37	7,72	5,76	3,72	5 1,79	0,90	0,00
j Ун	0,00	-0,85	-1,51	-2,53	-3,21	-3,76	-4,43	-4,86	-5,24	-5,28	-5,23	-4,92	-4,35	-3,41	-1,97	—1,08	0,00

Табл 3. — Аэродинамические коэфициенты. Дужки RAF-30

1	-2е	0°	2®	4°	6°	1 8°	10°	12°	14°	16°	3 8° ·	20°
С»	—0,058	0,003	0,068	0,135	0,202	0,266	0,327	0,388	1 0,419	1 0,432	0,427	0,398
Сх 1 i	0,0045	0,0042	0,0050	0,0376	0,0114	0,0160	0,0216	0,0310	0,0525	0,0830	0,1125	0,1355
! 1 Cmz	-0,014	0,001 1	0,017	0,033	0,049	0,065	0,081	0,097	0,111	0,127	0,139	-

Дужки Р-П-16

α°	-4°	— 2°	с°	2°	4°	6°	8°	1G°	12°	14°	16°	18°	20°	22°
i	-0,028	0,038	0,105	0,173	0,239	0,303	0,373	0,441	0,507	0,571	0,631	0,688	0,733	0,729
1 сх	0,0070	0,0071	0,0081	0,0105	0,0145	0.0200	0,0265	0,0341	0,0435	0,0540	0,0658	0,0783	0,0930	0,1130
Cmz i	0,018	0,034	0,050	0,066	0,083	0,100	0,117	0,135	0,152	0,169	0,184	0,198	0,212	0,213

Дужки B-S-16

, а	0°	2°	4°	6°	8°	10°	12°	14^	16°	18°	2 С·
Су	0,048	0,108	0,173	0,237	0,287	0,330	0,371	0,405	0,430	0,450	0,447
( С*	0,0064	0,0072	0,0099	0,0142	0,0200	0,0267	0 0350	0,0451	0,0579	0,0720	0,0895
i @mz 1_	0,014	0,033	0,048	0 062	0,071	0,081	0,089	0,097	0,104	0,106	0,099

кромкой. Минимальный коэф. профильного сопротивления профиля В—S не велик, однако не велик и С_утах. Профиль В—S характеризуется еще нулевым значением С_то (С_т при С_у=0); последнее объясняется обратной кривизной хвостовой части профиля. Такая модификация профиля уменьшает его С_утах, однако достигается постоянство центра давления. Кроме того по мере увеличения обратной кривизны

профиля уменьшается момент, скручивающий крыло. Впервые профили такого типа были предложены Мунком [¹⁵].

При испытании моделей крыльев, а также на практике в условиях натуры следует обра

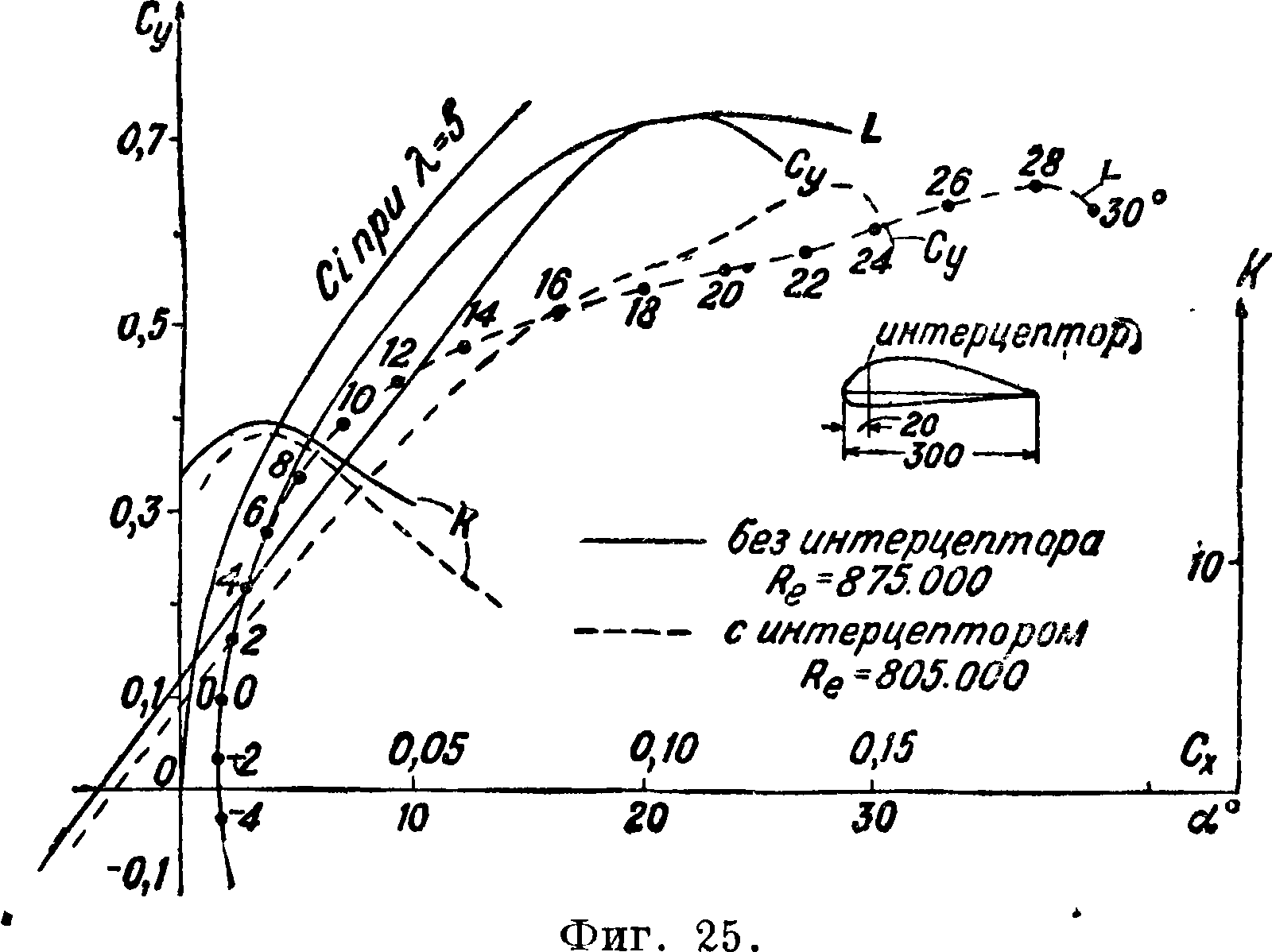
щать внимание на тщательную отделку их поверхности, особенно верхней поверхности. На фигуре 25 приведены результаты испытания в трубе Т-I ЦАГИ гладкого прямоугольного крыла н результаты испытания этого же крыла с интерцептором высотой 2 миллиметров, укрепленным перпендикулярно к верхней поверхности, как это показано на схеме. Длина интерцептора равнялась 0,2 метров при размахе крыла /=1,5 метров Интерцептор был укреплен в середине крыла. Из сравнений кривых видно, что при малых углах атаки поляры Лилиенталя практически совпадают, наоборот, при а >6° лобовое сопротивление крыла с интерцептором резко возрастает, а произ-

dCt,

водная уменьшается; уменьшается также Сутах- Это явление вызывается преждевремен ным срывом потока с верхней поверхности крыла

Г16 17 18 19 201

L » _{5 5}, J·

Для систематизации результатов испытаний профилей крыльев форму профиля характеризуют рядом его геометрич. параметров, из которых основными являются: толщина, вогнутость, положение максимальной вогнутости и кривизна носика профиля. За параметр толщины прини мается относительная толщина а₀=~ _f

где“ σ — максимальная толщина, а b — хорда. За параметр вогнутости принимается относительная в о-

^Г V ^т О С Т Ь Wq— —____^ентральная дужка

= - централь-

ной дужки, где w — максимальная вогнутость центральной дужки,

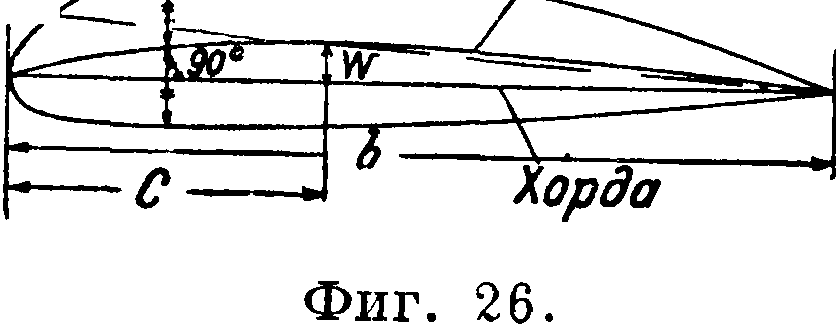
или относительная вогнутость д₀ — γ

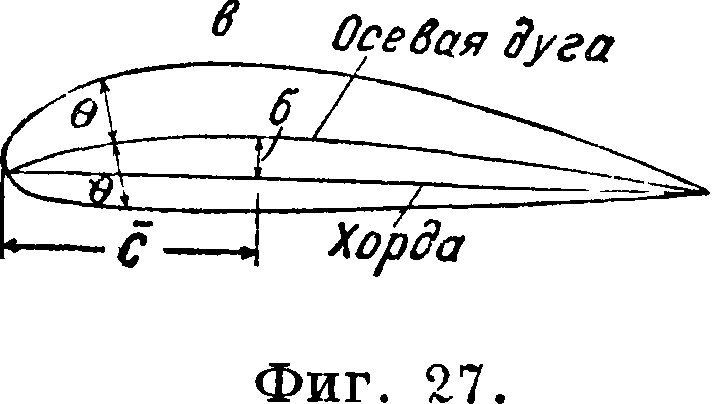
осевой дуги, где δ — ее максимальная вогнутость. Для построения центральной дужки (фигура 26) к внутренней хорде профиля проводится ряд перпендикуляров до пересечения с контуром профиля. Геометрическое место точек, лежащих посредине этих отрезков, есть центральная дужка. Для построения осевой дуги (фигура

27) контур профиля пересекается рядом прямых, наклоненных под равными углами к контуру. Геометрическое место точек, лежащих посредине этих отрезков, есть осевая дуга. За параметр положения максимальной вогнутости принимаются величины с₀=® (фигура 26) или с₀ =

(фигура 27). За параметр кривизны носика принимается относительный радиус кривизны носика, равный ϋ₀=^-, где ii—радиус кривизны носика профиля. Величины σ₀, w₀,

^со> ^со “ часто даются в процентах от хорды. Прямая, соединяющая точку максимальной вогнутости центральной дужки и хвостик профиля, дает с точностью до 0,5° направление потока, при к-ром С_у=0 [²¹, ²²].

Наиболее полный анализ аэродинамич. свойств профилей в зависимости от их геометрич. параметров провели Jakobs, Ward и Pinkerton [²³].

Фигура 28.

Ими была исследована серия профилей NACA* испытанная в трубе переменной плотности при ее третьем варианте. В этой серии номер профиля одновременно характеризует и геометрич. параметры профиля, а именно: первая цифра

R.^JJO⁶

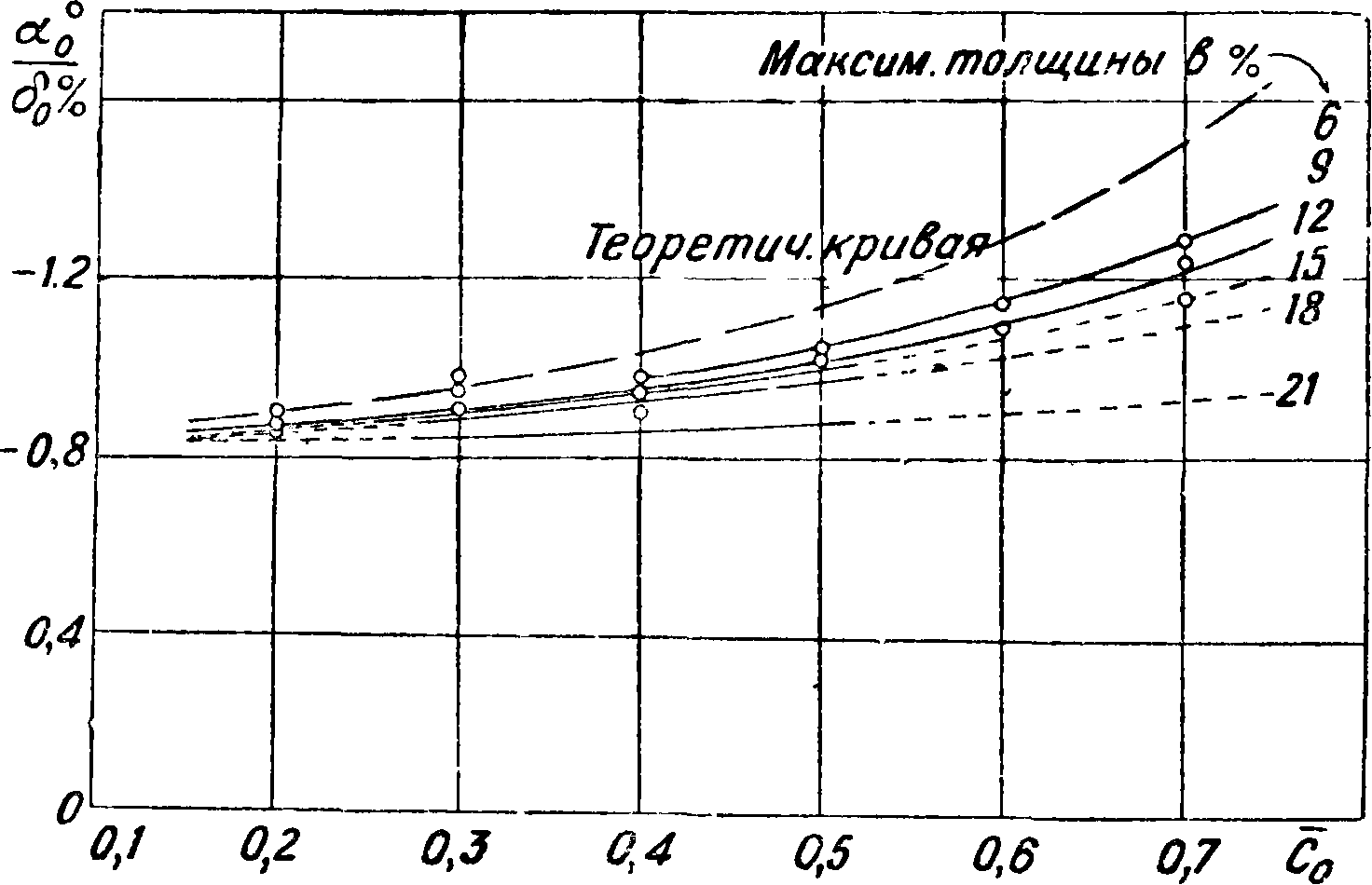
указывает вогнутость <5₀ в %, вторая цифра — положение вогнутости в десятых долях хорды и две последние — относительную толщину в % от хорды. На фигуре 28 приведен график изменения отношения ~ (а₀ —

угол атаки при С =0) в зависимости от положения вогнутости и максимальной толщины; кроме того приведена кривая, подсчитанная по теории тонкого профиля [²³, 24_} 25_? 26 27]. На фигуре

29 даны значения а₀=при Я=ар в зависимости от относительной толщины профиля. Согласно теории тонкого крыла Oq=π в действительности (фигура 29) вследствие потерь, вызывае-

J0 15 20 25 6₀%

Фигура 29.

dC-

мых вязкостью, а₀<тг, причем а₀ убывает при увеличении сг₀. Было обнаружено, что в области 0,2 < с^<0,4, то есть для наиболее употребляющихся профилей, а₀ от ζ практически не зависит.

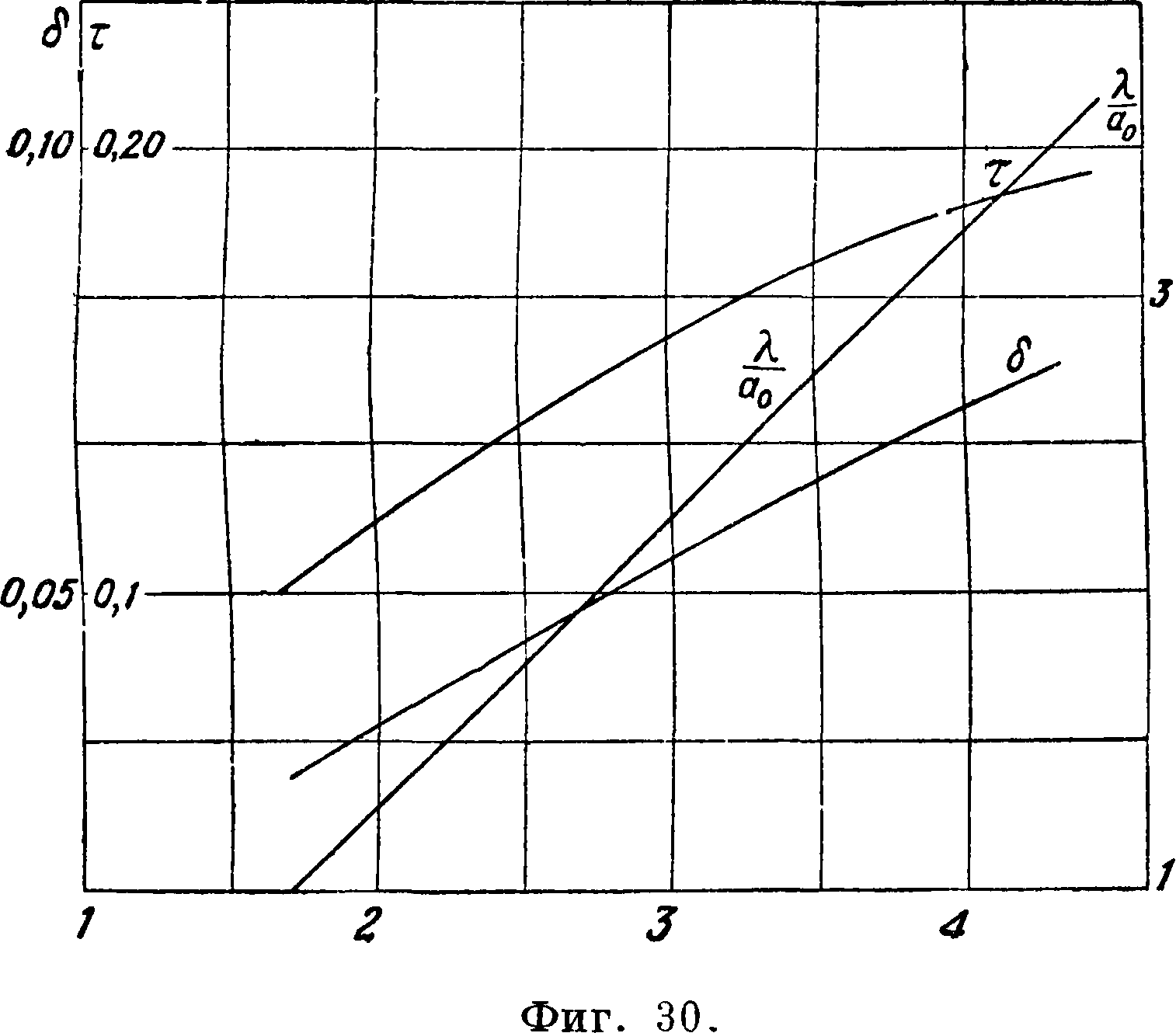
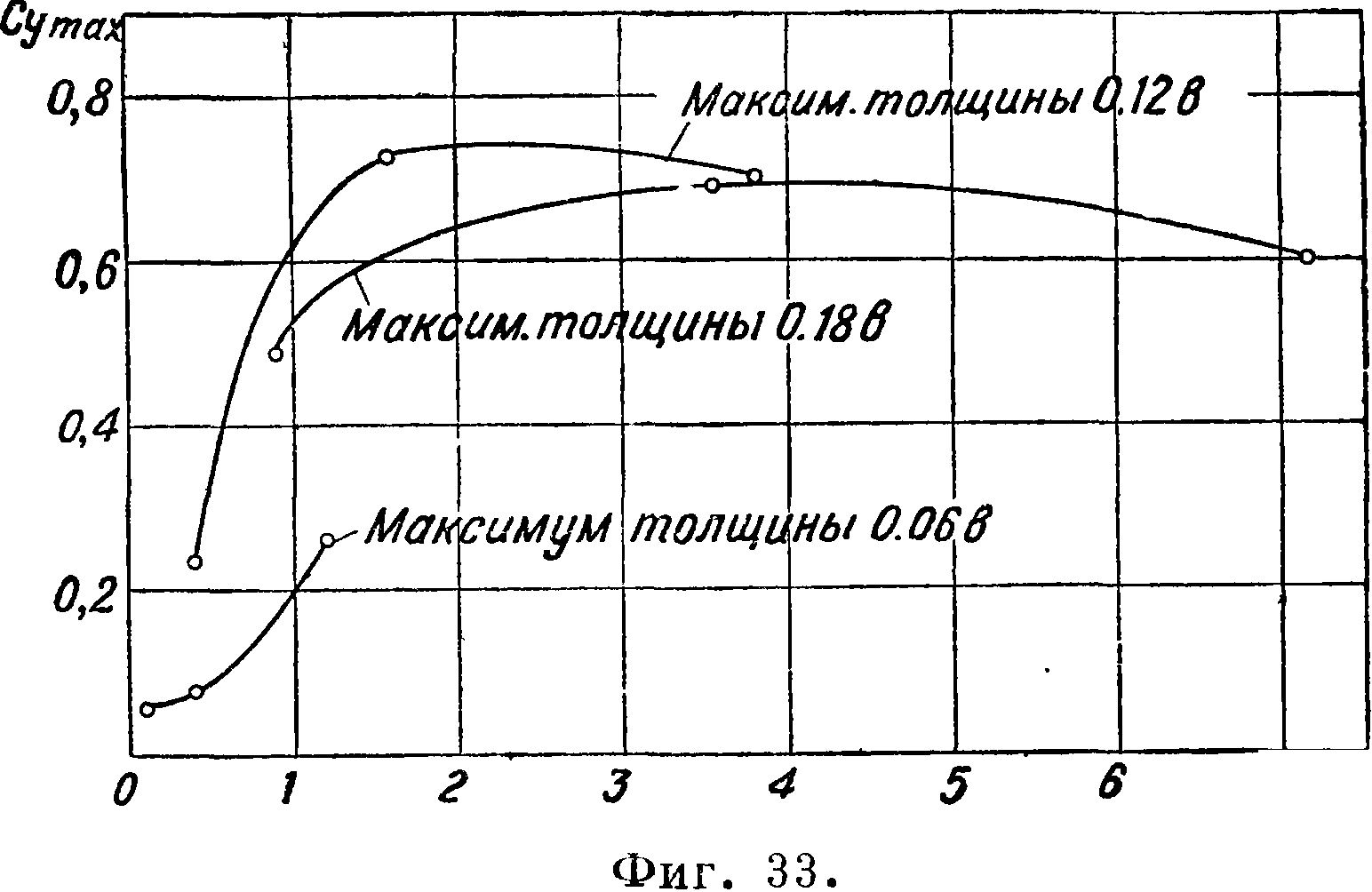
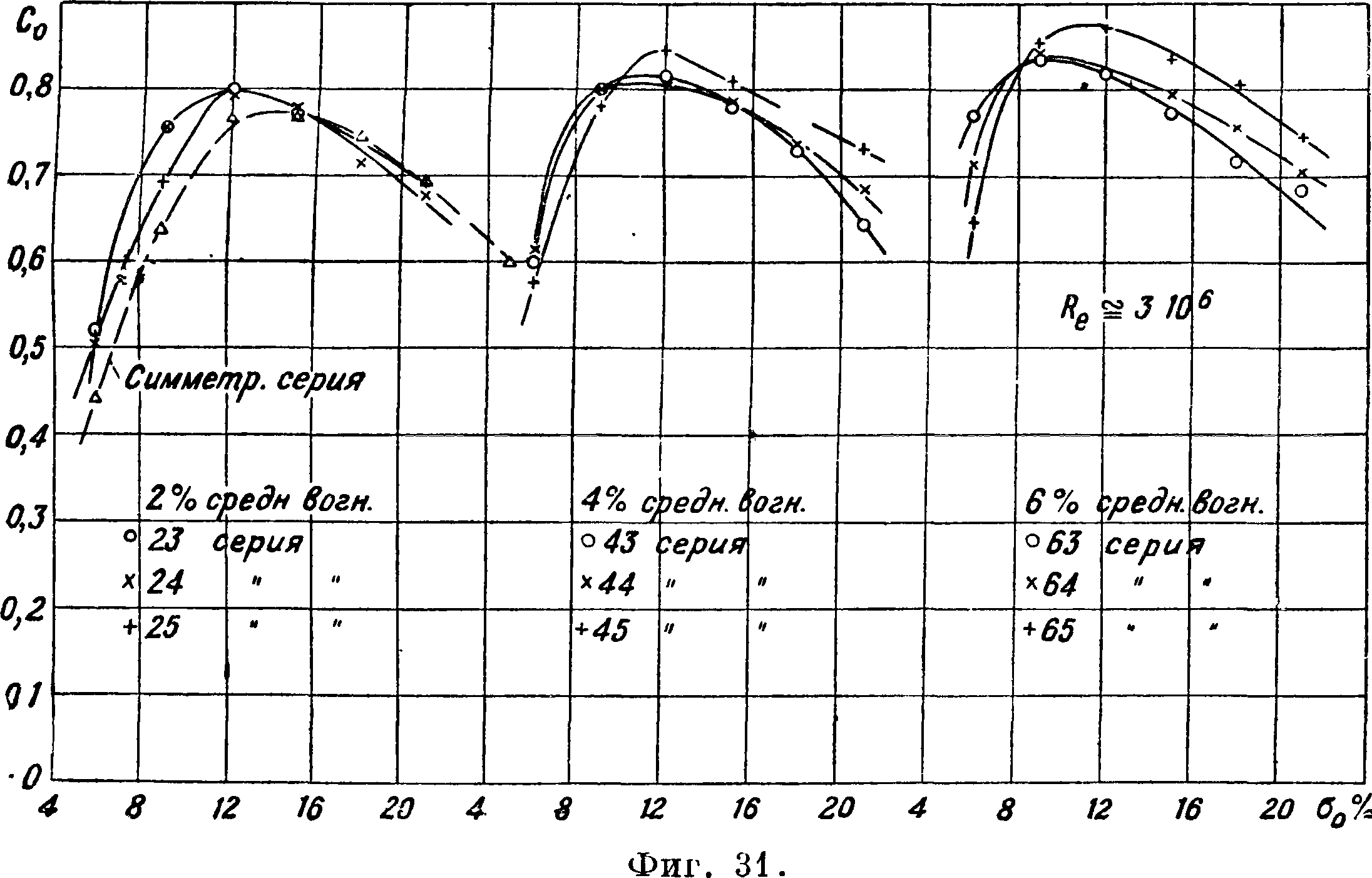
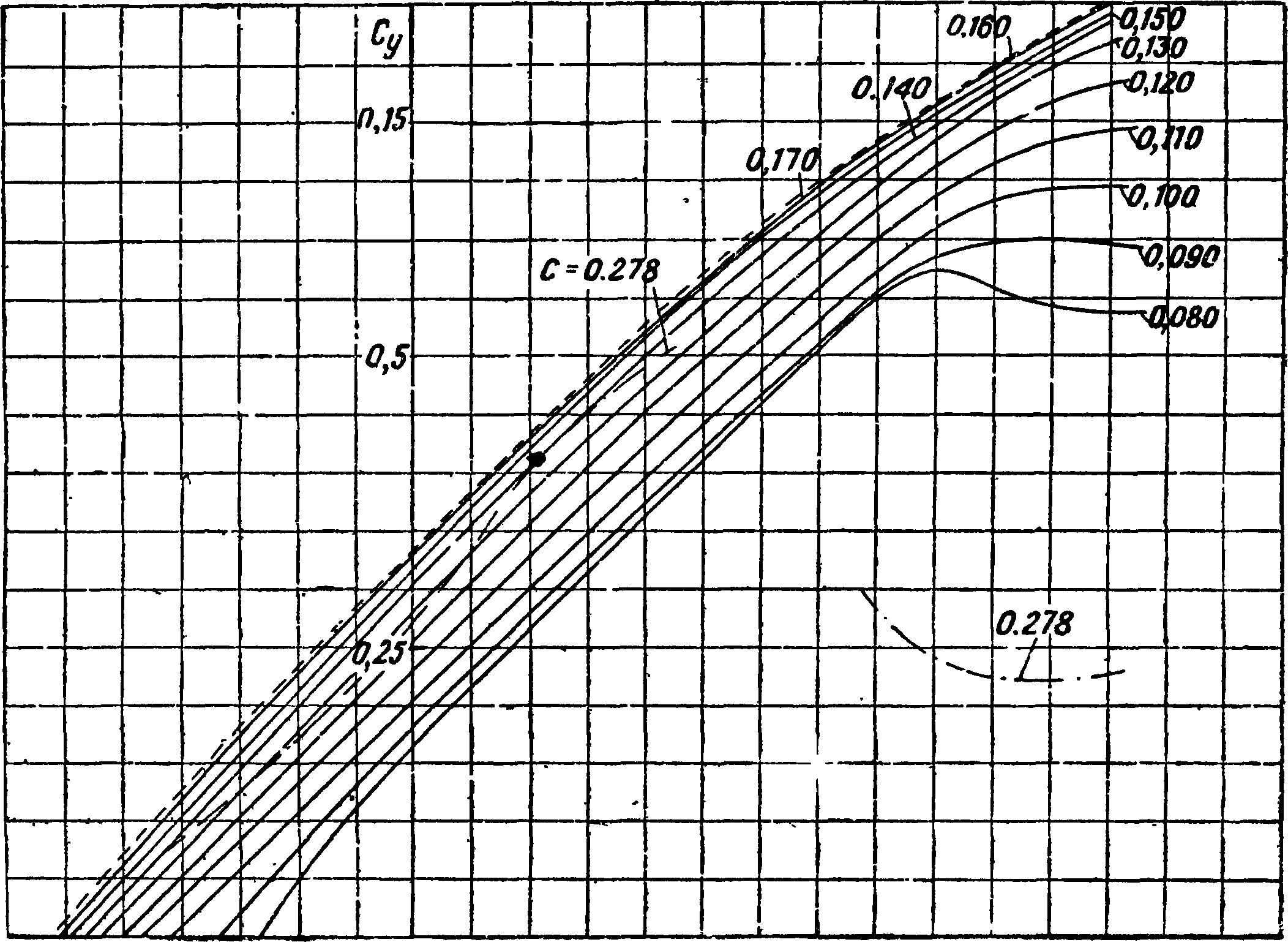
Значения т ф-ии — приведены на фигуре 30. Зависимость 0^ _тах от б₀, с₀, ег₀ и R₀ приведена на фигуре 31,32 и 33. При пользовании этими графиками следует помнить, что Су max ^в значительной Су_тстепени зависит от числа Рейнольдса и турбу- °~ лентности [⁶,⁷,¹³,¹⁹,^{28 29} ]. Было обнаружено о,9-[²*]> что С_ятах профи-лей с малой вогнуто- о,8стью (с5₀ < 0,04) растет· с увеличением числа 0,7-Рейнольдса, для профилей с большой во- о,б -гнутостью (<5₀ > 0,065) найдена обратная за- о,5-висимость, для профилей средней вогнутости Сушах приблизительно _фиг. 32.

постоянен. На фигуре 34

приведена зависимость С_{у тах} от числа Рейнольдса при различных начальных турбулентностях, найденная Милликеном и Клейном [⁷]

х
			А С4
	4==	/г
-		Среди вогк		f.
-г Си	ммеп	ip. npt	криль

7 в₀%

для профиля NAGA 2412. Повышенная турбулентность вызывалась проволочной решеткой, устанавливавшейся на различных расстояниях от модели крыла. Рассмотрение диаграммы показывает на значительное возрастание С _тах вместе с

Увеличение с₀ от 0,4 до 0,7 уменьшает а₀ на 5%. Если величина а₀ известна, то α=^~ при конечном и заданном Я находится по фигура 30 [²⁷]. Скос потока находится по ф-ле

Δα° =-§ (! + тонн). 57,3.

Фигура 34.

увеличением Re и τ. Влиянием турбулентности объясняются наблюдающиеся иногда совпадения в С_утпх1 найденных по опытам в аэро-динамич. трубе при малых числах Рейнольдса и в полете при больших числах Рейнольдса. Увеличение турбулентности не всегда вызывает увеличение С_утах для профилей с большой вогнутостью была обнаружена обратная закономерность [¹³].

Коэф. момента для летных углов атаки приближенно м. б. вычислен по ф-ле

Сжо + тСу,

где коэф. т теоретически равен 0,25. Опытным путем установлено, что этот коэф. для прямоуголь

ного крыла в зависимости от формы профиля меняется в очень узких пределах, а именно:

0,23<>г<0,25, причем он уменьшается по мере увеличения σ₀, <5₀ и с₀. Расстояние центра дав-

где С_п=С_у · cos а + С_х · sin а; при — 6° < а < < 20° С_п^С и поэтому s=100 -^^w-.

Су

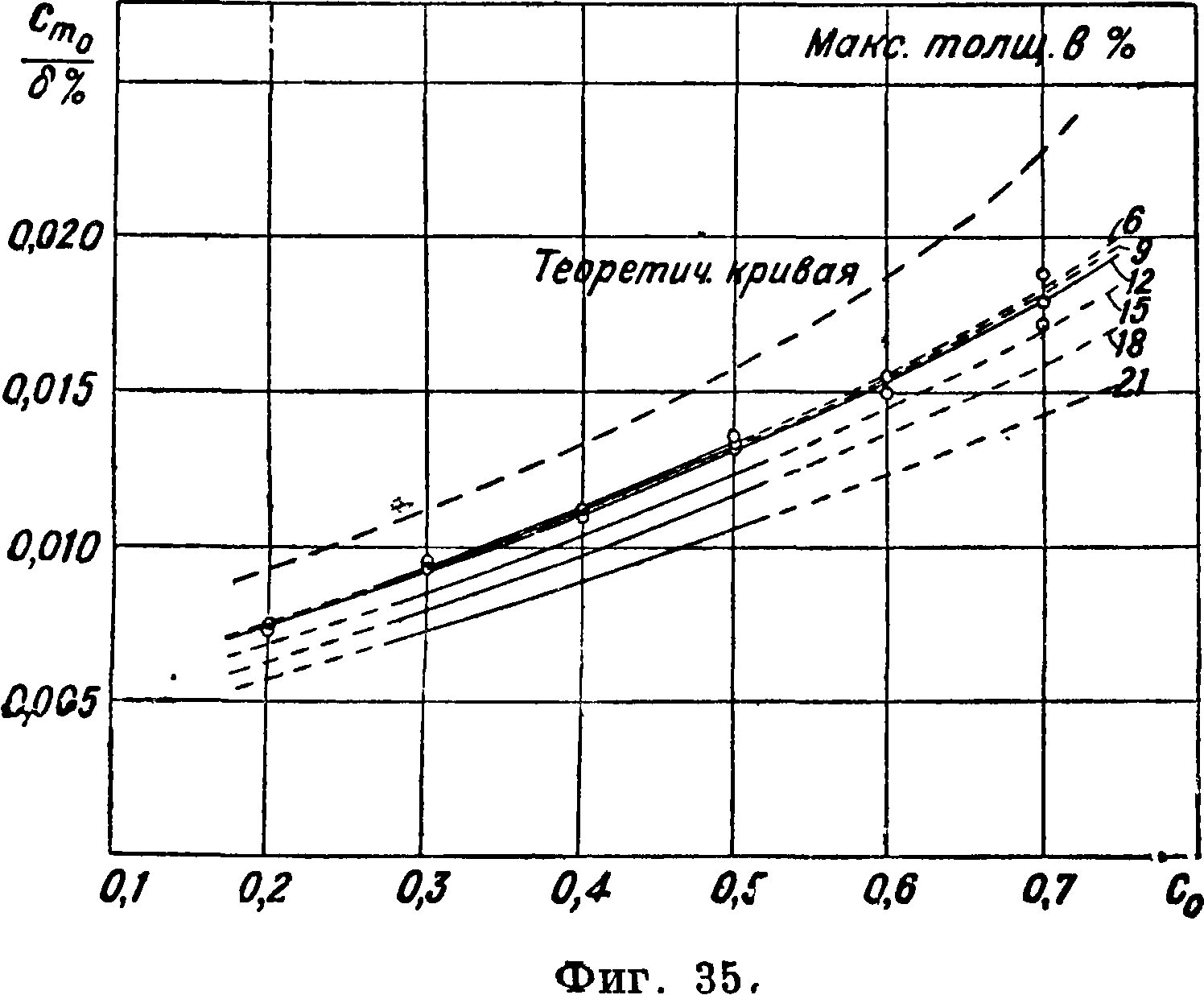
О зависимости коэф-та т от формы в плане см. [²⁷, ³⁰, ³¹]. На фигуре 35 приведена зависимость от положения максимальной вогну тости и от относительной толщины профиля; кро

ме того дана теоретическая кривая, подсчитанная согласно теории тонкого крыла [²³, ²⁴, ²⁵, ²⁶, ²⁷].

Лобовое сопротивление крыла м. б. разложено на 1) индуктивное сопротивление и 2) профильное сопротивление. Индуктивное со-Р противление обусловливается скосом потока перед крылом и зависит от очертания крыла в плане, закрутки и удлинения. Теория индуктивного сопро-

р по верхней поверхности

Фигура 39.

тивления (смотрите) крыла разработана до практического применения Прандт-лем, Бетцем, Мунком, Трефтцем и Глауэртом [²⁷, ³², ³³, 34, 35₁ 36^ 37_? 39₅ 40^ 41_? 4_2> 43]

Для прямоугольного крыла коэфициент индуктивного сопротивления определяется по формуле

⁼ тГГя * (1 +

величина д находится по фигура 30. Профильное сопротивление зависит от формы профиля и со

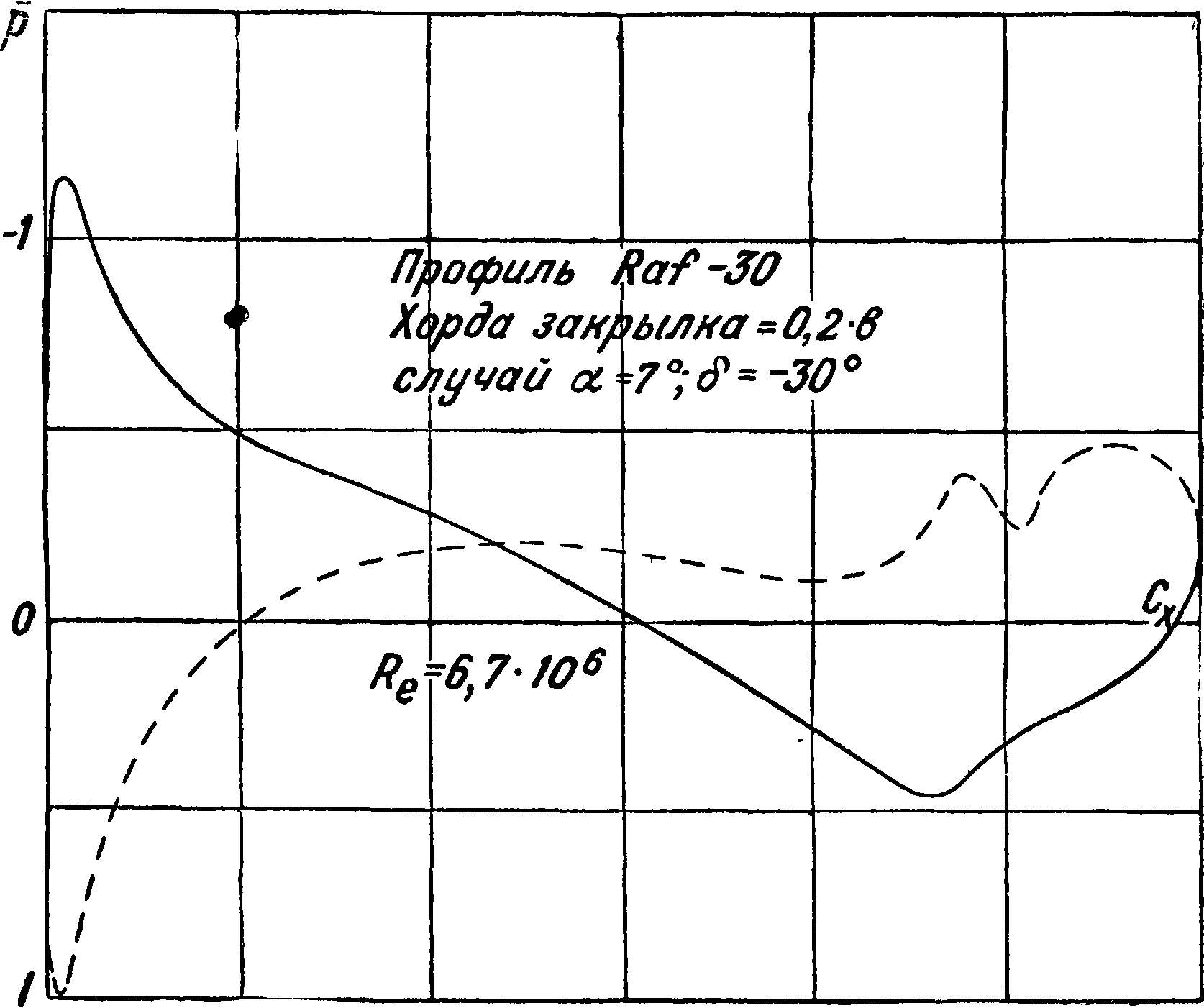
стояния поверхности. Коэфициент профильного сопротивления определяется как разность между полным коэф-том сопротивления и коэф-том индуктивного сопротивления, то есть С_р=С_х — С_£. Анализ испытания различных профилей показывает, что при данном состоянии поверхности минимальная величина С_р тем больше, чем больше

	Пр Щ сл^	криль R да закрк /чай ос =	if-30 чл/гα=0,4 7°; <? =0	?:в о
		Ьяв,7·	« we;
1					&
			---	N	1 у
L

Фигура 41.

сг₀ и w₀ или <5₀. Имеется большое количество ф-л для определения коэф-та С_р, но все ф-лы недостаточно точны, т. к. они не учитывают влияния числа Рейнольдса и турбулентности. Ф-ла Хиггинса [“] для симметричных профилей, выведенная на основании опытов в трубе переменной плотно-

Профиль Rot-JO Хорда закрылхα=0,2-Ь случаи сс=7°, ή

R_e*6, 7-Ю*

7-

Фигура 42.

сти (Re =3 100 000) при ее втором варианте (R_c =154 000), имеет вид

^Cpwin=0,0028 + 0,005 σ₀ + 0,05 og.

Ф-ла Гласса [¹⁶], выведенная по опытам, проведенным в трубе НК-I МАИ (Re=330 000 и R_c== 150 000), имеет вид

^Ср ™;п=2Ть * ⁰’^{0008 +} °’^{0375 σ}° + °’⁶⁴³ где П — периметр профиля. На основании обработки испытаний в трубе Т-I ЦАГИ (Re—1 000 000 и R_c =150 000) ряда употребляющихся в настоящее время профилей как симметричных, так и несимметричных м. б. предложена следующая приближенная ф-ла:

С_р=0,00155 + 0,028 σ₀ + 0,0058 C_v -- 0,0056 Cg + 0,055 - Cg.

Ф-ла применима при 0,1 < С_у <; 0,5. Все приведенные ф-лы выведены по данным испытаний полированных крыльев [^1в, ²³, ⁴⁶, “]. О вли янии состояния поверхности см. [¹⁶,¹⁷, ¹⁸,¹⁹,²⁰].

Фигура 43.

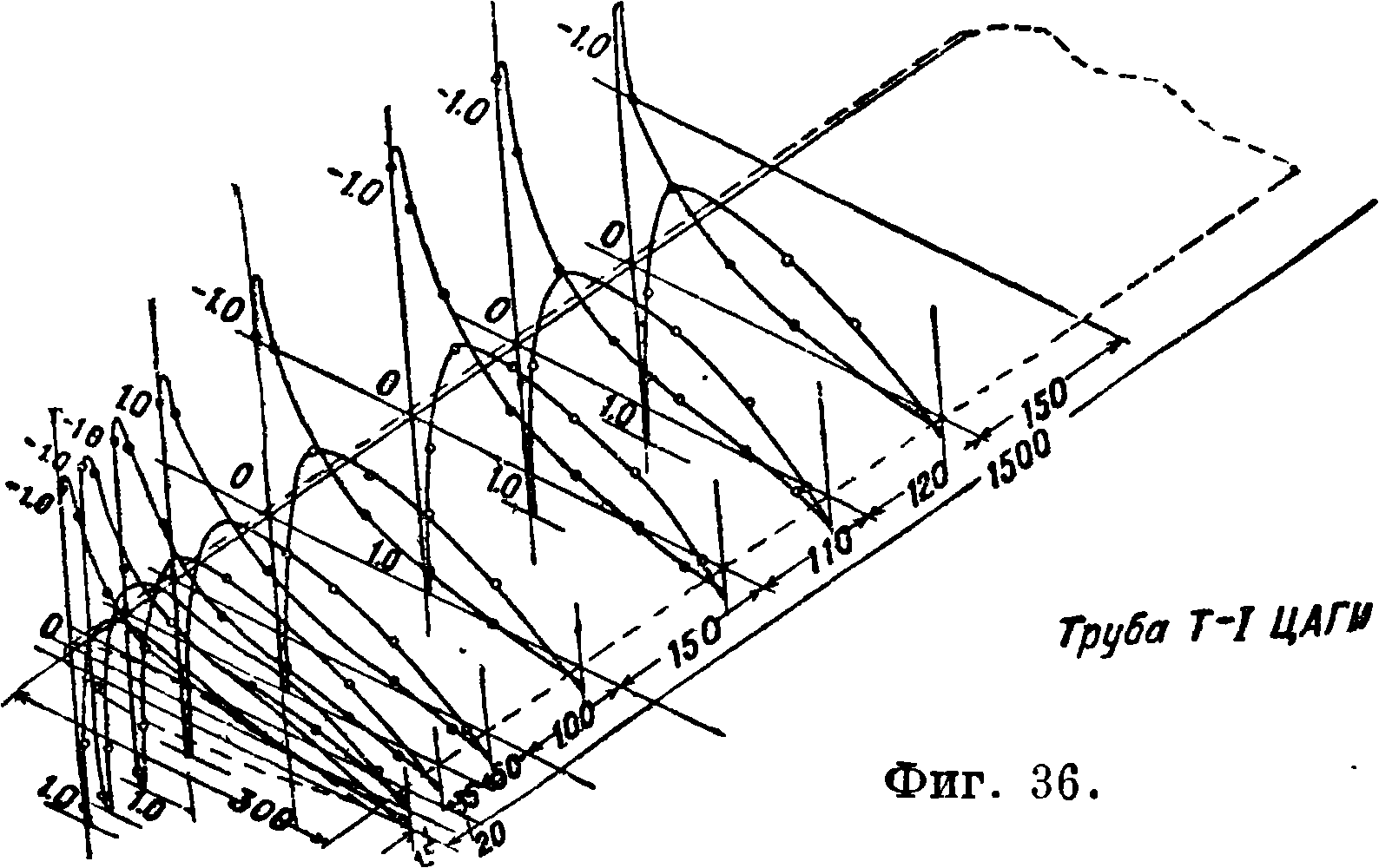
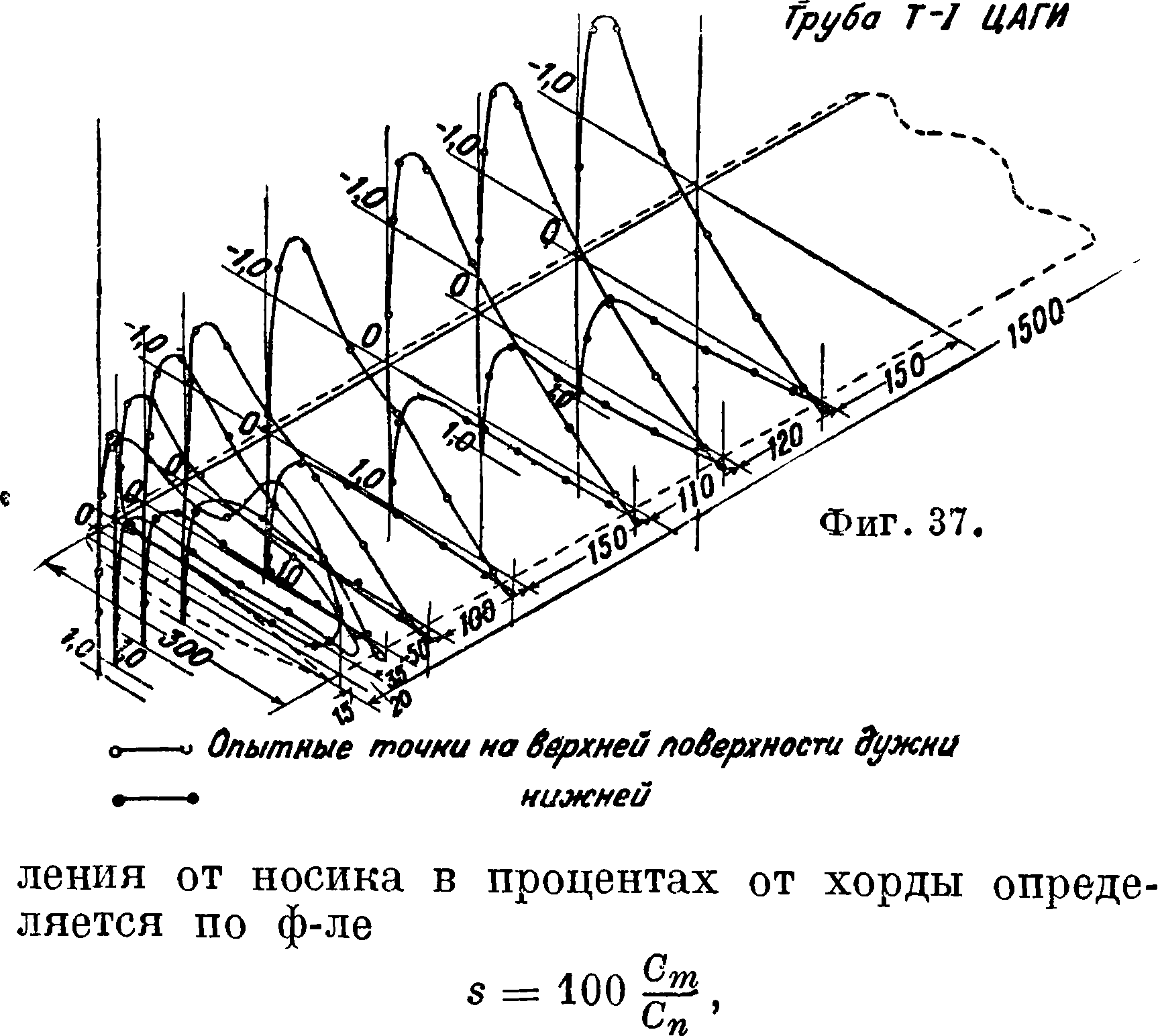
На фигуре 36, 37 и 38 приведено в аксонометрических проекциях распределение давления по полуразмаху прямоугольного крыла (Я=5). Как это обычно ради удобства принято, коэф. давления р отложен не перпендикулярно к поверхно-

1 J_, _,
К=2Л	1 i
_1__

-6-

Фигура 44.

сти, а перпендикулярно к хорде крыла. Случай а= — 4°20 соответствует С_у=0. Случай α= 8° (фигура 37) соответствует летному углу атаки при еще вполне устойчивом обтекании крыла; на это указывает линейный закон изменения давления на верхней поверхности в области положительного градиента давления. На концах крыла обнаруживается нарушение закономерности и пучности разрежения на верхней поверхности. Последнее вызывается присосавшимися в этом месте концевыми вихрями. Случай а=20° соответствует максимуму С_у (фигура 38). В этом случае

вблизи концов крыла обтекание еще совершается без заметного срыва потока; наоборот, в середине крыла поток уже сорвался с верхней поверхности, что видно из нарушения линейно-

го закона изменения давления. Если нет какой-либо искусственной причины, вызывающей срыв потока, то срыв обычно начинается в середине крыла, а потом уже распространяется по всей поверхности его. На фигуре 39 приведено распределение давления по сечению крыла с профилем В-18 в случае С_у=0. Это профиль мунковского типа с обратной кривизной средней линии и С_и _ ~ ~

ние фигура 36 и 39

Фигура 46.

указывает на причину, вызывающую нулевое значение С_т0 у профилей мунковского типа. Методы определения теоретического распределения давления по произвольному профилю см.

[38 _? 47 48 _? 49J

Профиль дужки PIJ (исходное, не разрезное крыло]

150

Профиль дужки Р~Ио (крыло с закрылком)

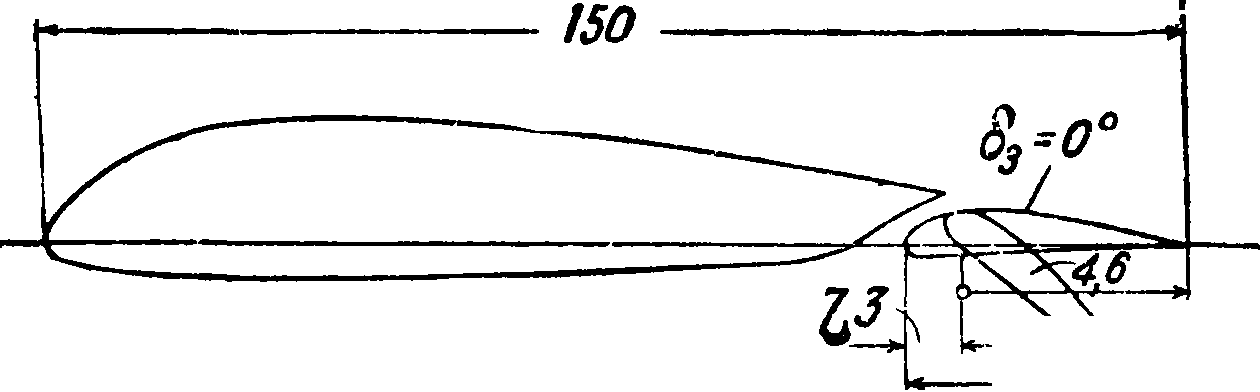
375-

Профиль дужки РIIЬ и обозначения координат (крыло с предкрылком)

Профиль дужки Р~П с и обозначения координат (крыло с предкрылком и закрылком)

Фигура 47

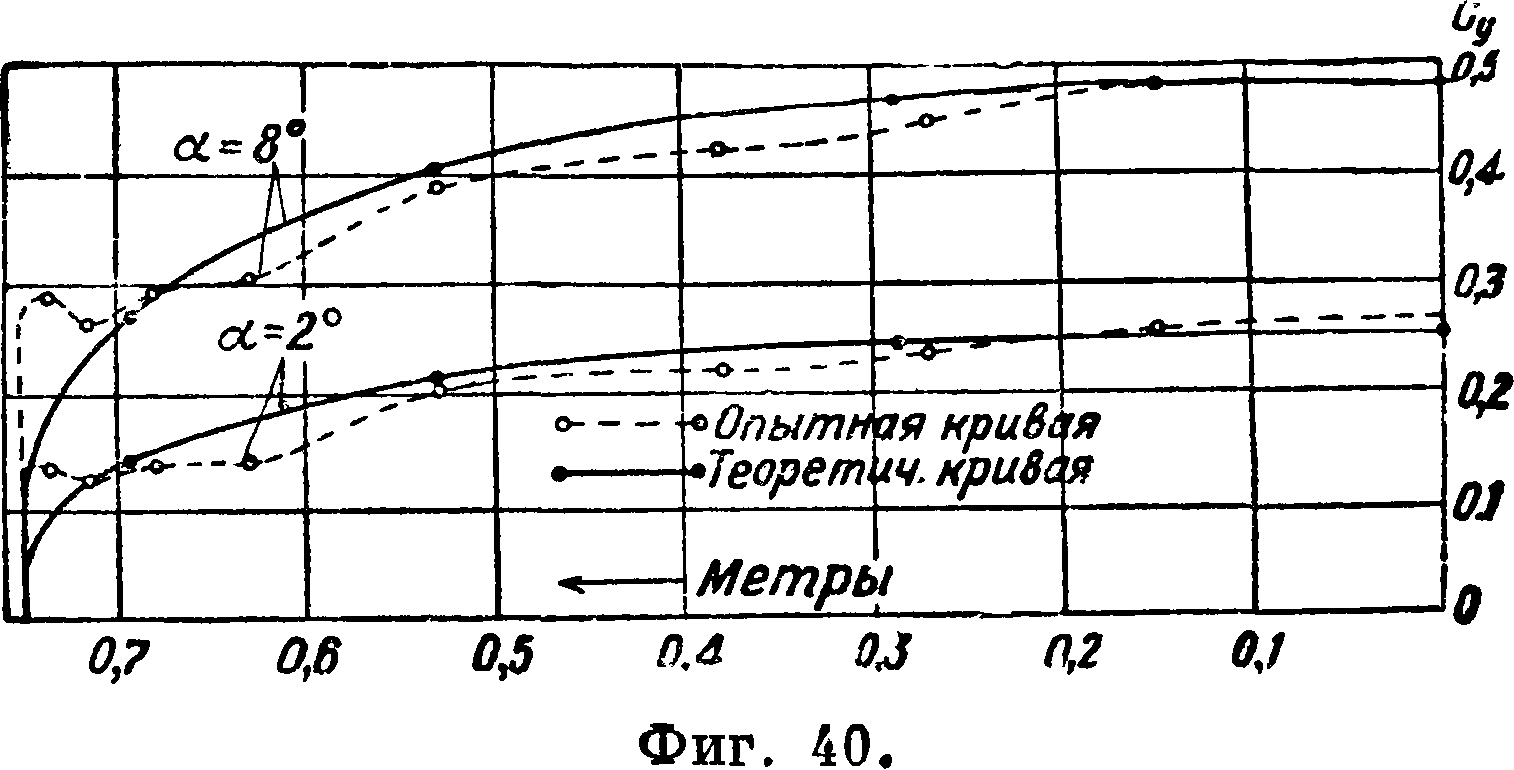
На фигуре 40 дано опытное и теоретик, распределение нагрузки при ρ=1, ν=1 и b=1 по полуразмаху прямоугольного крыла. Сравнение кривых показывает на вполне удовлетворительное совпадение за исключением концов крыла. В случае эллилтич. или трапецевидного очерта ния крыла в плане совпадение теоретических и опытных кривых много лучше. Совпадение кривых обычно наблюдается до углов атаки, при которых наступает нарушение прямолинейного закона изменения С_у по а. Теоретик, распределение нагрузки по размаху м. б. подсчитано согласно теории индуктивного сопротивления крыла [²⁷, ³², ³⁶, ³⁷, ³⁸, ³⁹, ⁴⁰, ⁴¹, ⁴², «].

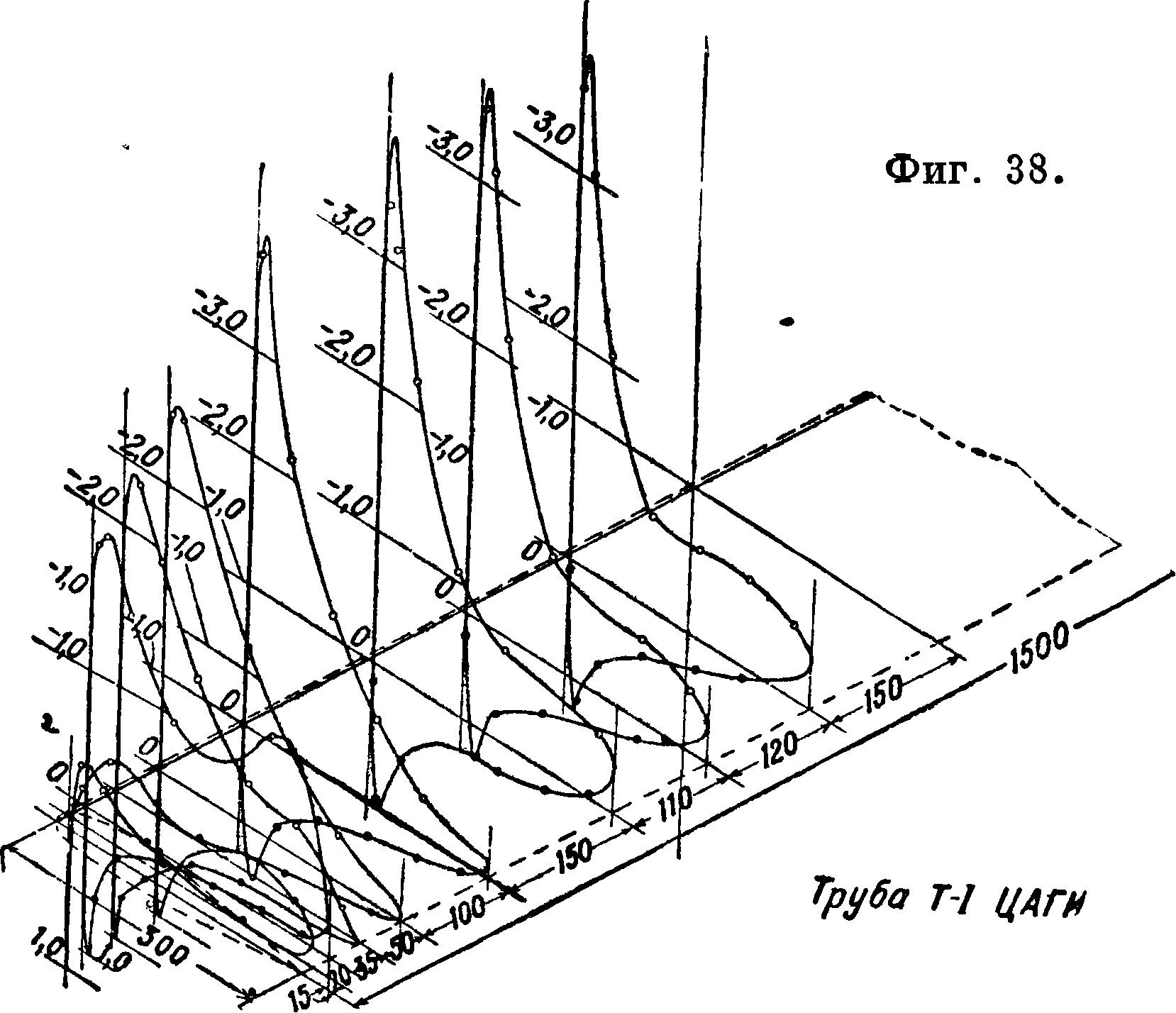
Опытное распределение давления по профилю и размаху крыла и оперению см. L⁵⁰, ⁵¹, ⁵², ⁵³, ⁵⁴, ⁵⁵, ⁵⁶]. На фигуре 41, 42 и 43 приведено распределение давления по сечению прямоугольного крыла с закрылком по всему размаху согласно опытам, проведенным в трубе переменной плотности [⁵⁷] при ее втором варианте (R_c=154 000). Диаграмма показывает характер распределения нагрузки

по профилю крыла при неотклоненных элеронах и при отклонении их на угол <5₃ =+30° (фигура 42, 43).

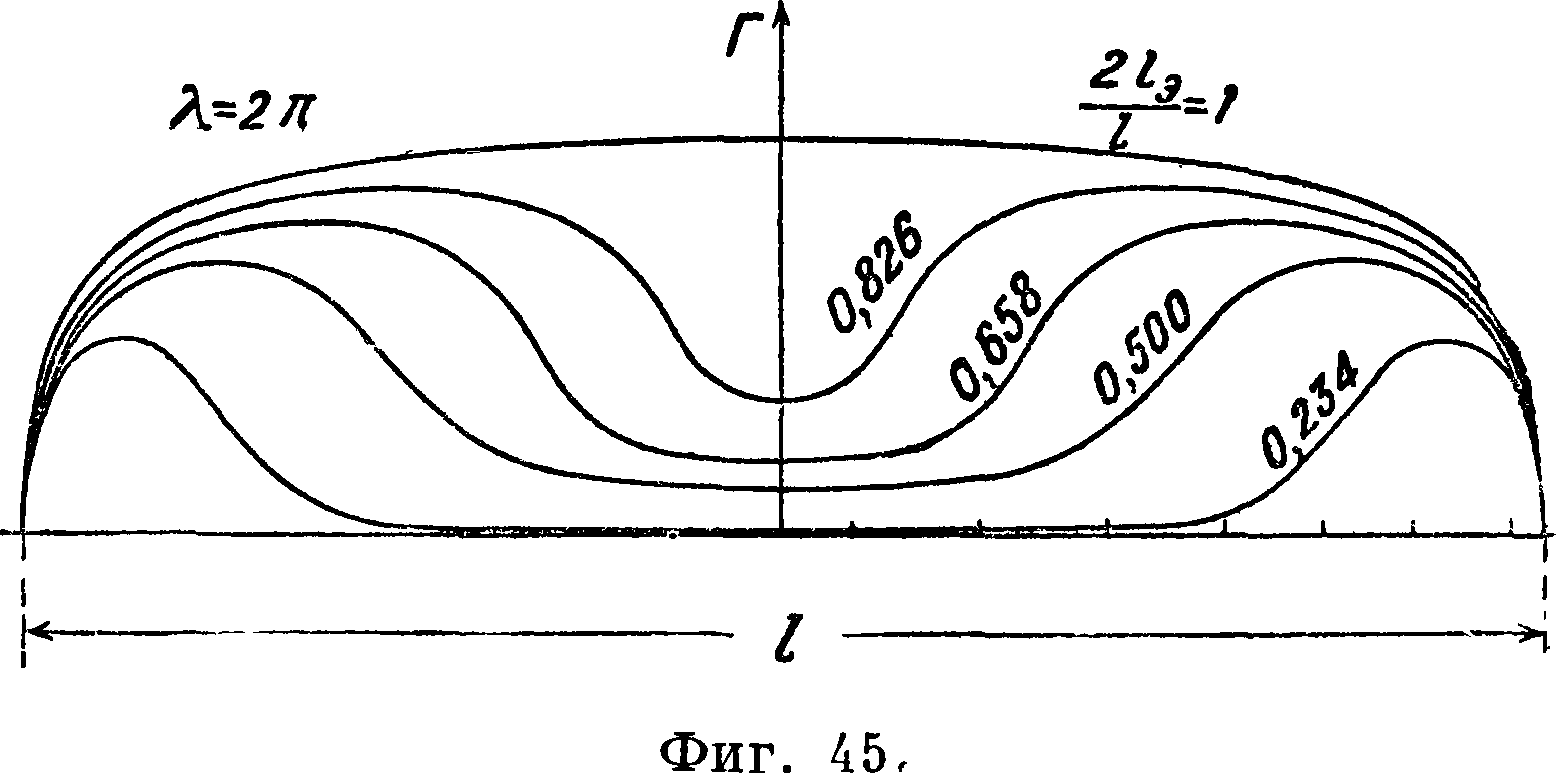
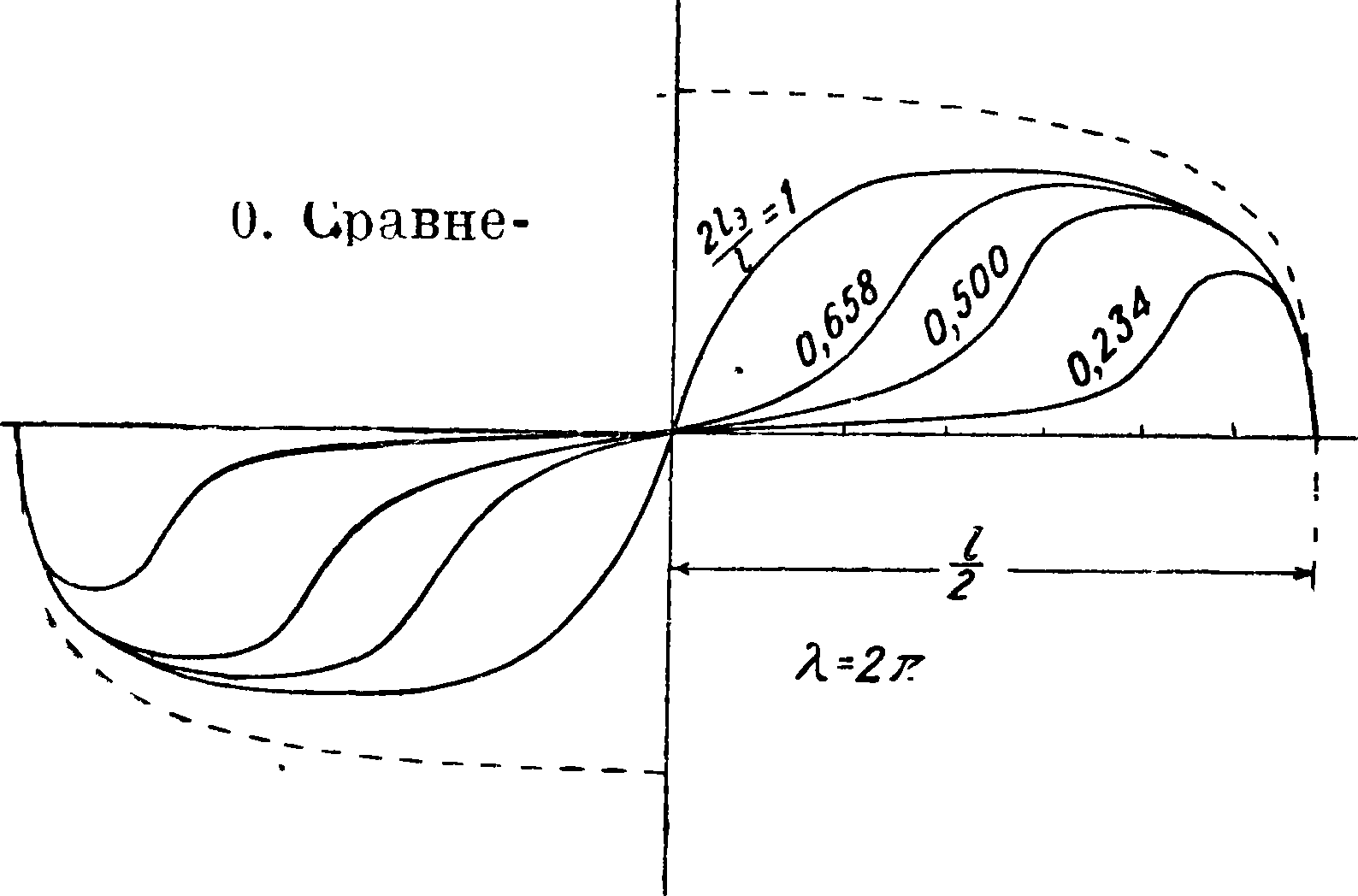
Распределение нагрузки по размаху крыла с элеронами или с закрылками (одностороннее отклонение элеронов) м. б. приближенно найдено теоретически [⁵⁸, ⁵⁹]. На фигуре 44 дана схема прямоугольного крыла с элеронами. На фигуре 45 приведено распределение приращения циркуля-

ции по размаху крыла в случае одностороннего отклонения обоих элеронов (случай закрылков). В этом случае, хотя элероны и не достигают середины крыла (за исключением=1) вслед ствие индуцированного скоса потока, в середине крыла возникает ^подъемная сила. На фигуре 46 приведено распределение приращения циркуляции по крылу с элеронами в случае их разно

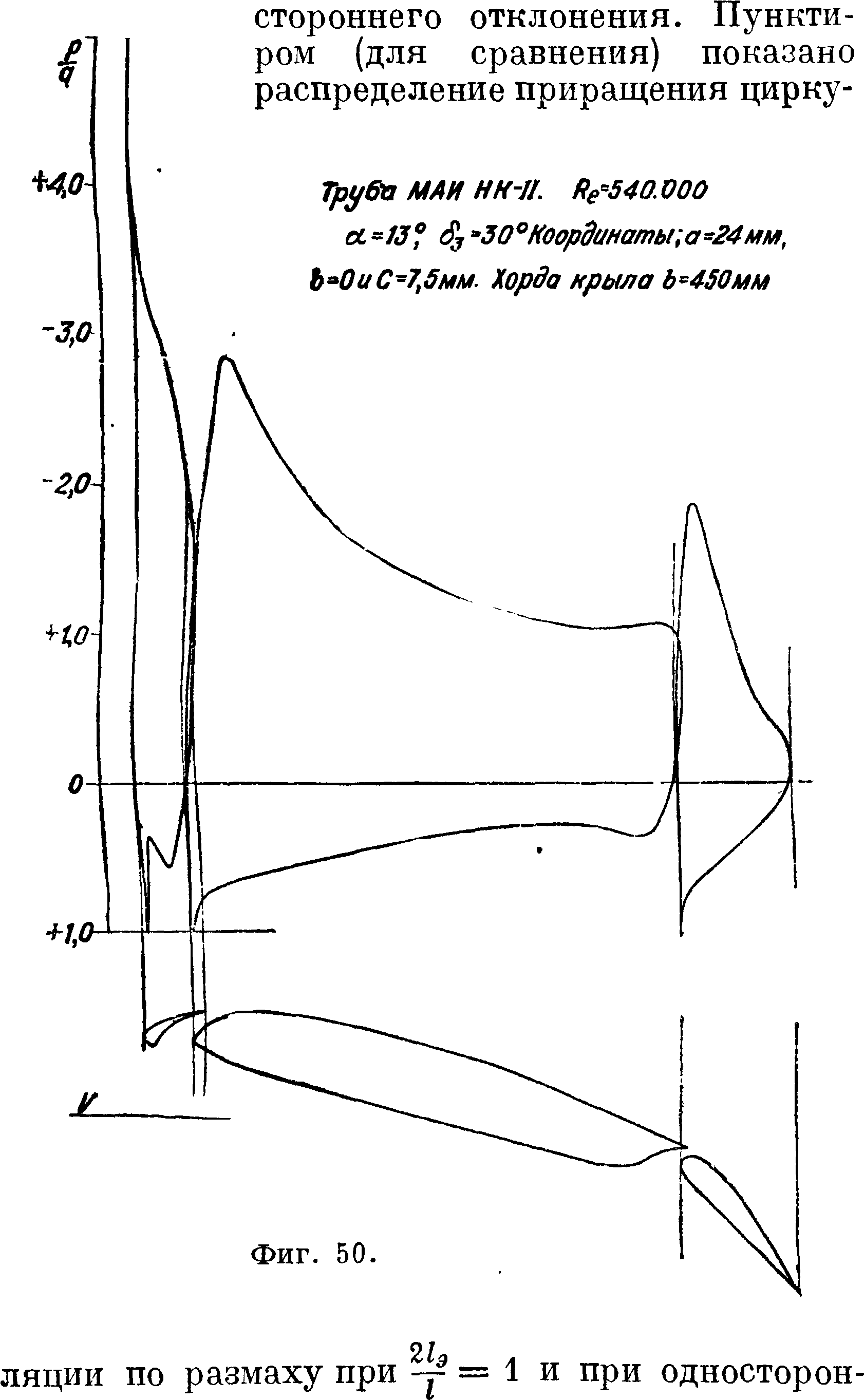
нем отклонении элеронов [⁵⁰, ⁶⁰, ⁶¹, ⁶², ⁶³, ⁶⁴, ⁶⁵, ⁶⁶, ⁶⁷]. VII. Способы повышения подъемной силы.

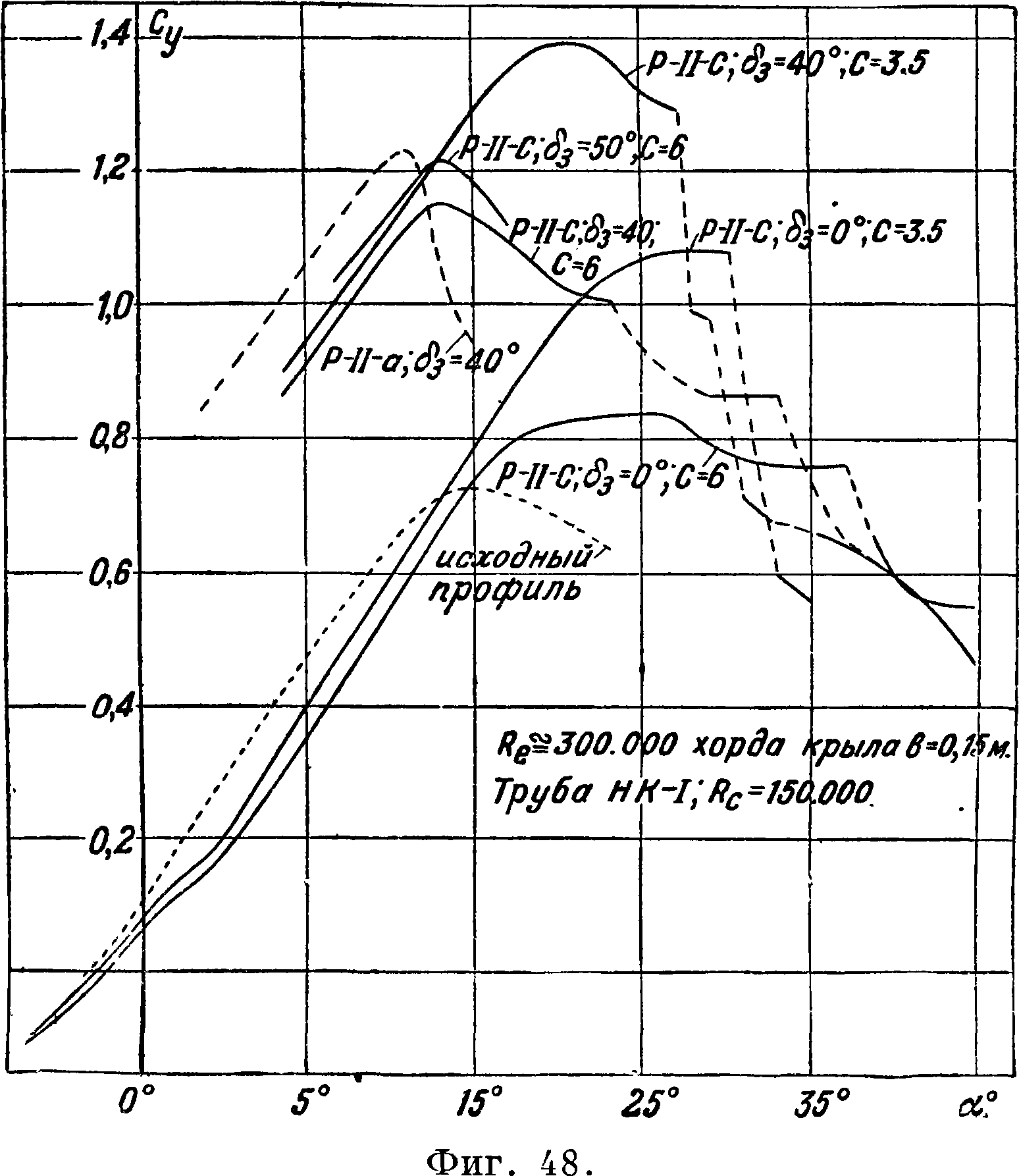
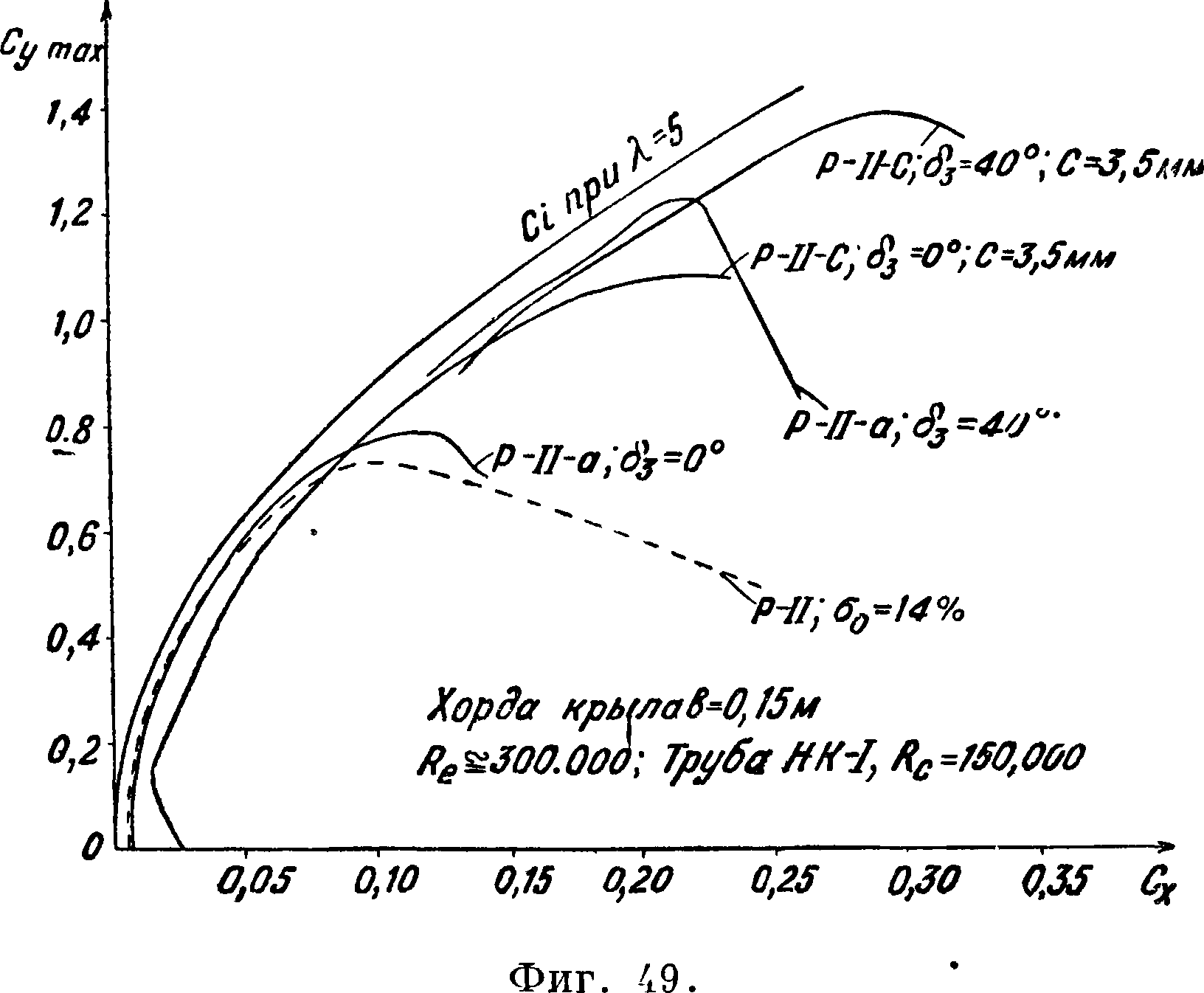
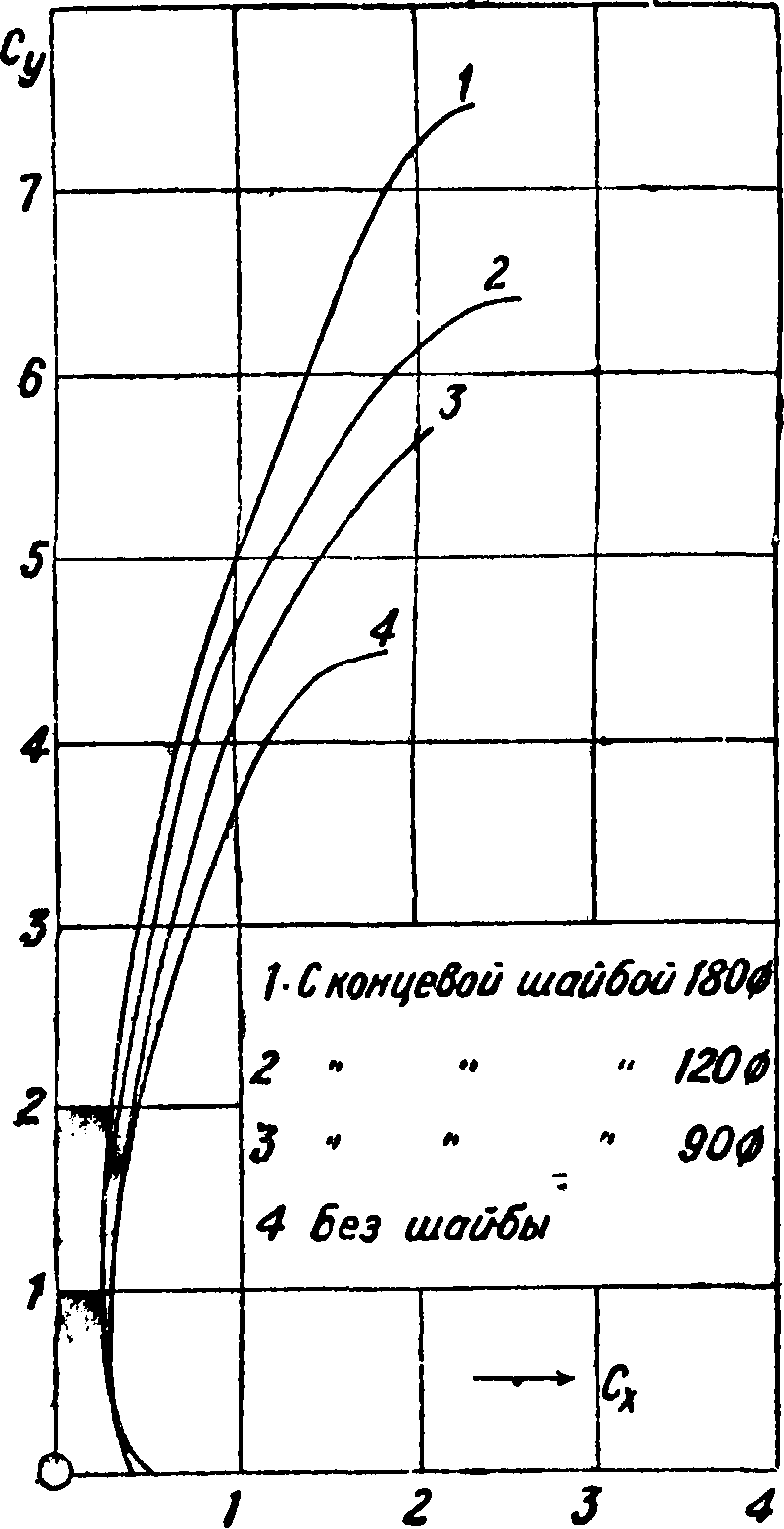
Для увеличения С_у крыльев можно применять разрезные крылья, крылья со щитками или производить отсасывание или сдувание пограничного слоя. Первые два способа нашли широкое применение на практике. Основные виды профилей разрезных крыльев (смотрите) приведены на фигуре 47; на ней же изображен исходный неразрезной профиль. Кроме указанных основных типов возможен еще целый ряд модификаций, но с принципиальной стороны их работа не отличается от работы приведенных основных трех типов крыльев. На фигуре 48 даны результаты испытания (в трубе НК-I МАИ) на С_у по а исходного неразрезного крыла и трех упомянутых разрезных крыльев с предкрылками и закрылками, расположенными по всему размаху [⁶⁸, ⁶⁹, ⁷⁰J. Для крыльев Р-Н-а и Р-Н-с угол д₃=40° является оптимальным, дальнейшее увеличение угла отклонения закрылка влечет уменьшение Су шах- У крыльев с предкрылками следует обра

-ъ=2оа-*

ч>₃—

Фигура 51.

щать внимание на правильный выбор положения предкрылка I⁷¹, ⁷², ⁷³]; особенно большое влия

ние оказывает координата с (фигура 48). На фигуре 49 приведены поляры Лилиенталя упомянутых крыльев. Наиболее неудачными в отношении

Разрез СО

. ШйтйА

; МОТОр^.

cQ контактный измеритель uucj [ Точки измерения явления

- /ООО -

Фигура 53.

сопротивления являются крылья с предкрылками (фигура 47 и 49), поэтому на практике предкрылок обычно делается выдвижным. При малых углах атаки предкрылок бывает плотно примкнут к

Зависимость Су_тах от нозфициеитов C_Q, C[_s u Ср

Фигура 54.

основной части крыла, а перед посадкой самолета он выдвигается или летчиком при помощи особого механизма или автоматически под влия-

нием аэродинамич. сил, действующих на предкрылок при больших углах атаки. С физич. стороны работа предкрылка объясняется затягиванием момента срыва потока вследствие скоса потока за предкрылком и увеличения кинетической энергии пограничного слоя на верхней поверхности, а также вследствие собственной подъемной силы предкрылка. Работа закрылка в основном обусловливается увеличением во-

во позволяет увеличить крутизну траектории самолета при посадке в 3—4 раза. В табл. 4 приведены основные данные разрезных крыльев различных типов; при пользовании таблицей следует учесть, что С^_тах= fjymax 69^ 70^

72 73 74 75 76 77

у max 79].

71

7.J

0,9

0J

0,5

0,3

0,1,

"v

X—

_

п

У

А

У

У

α-----у „ 7 +----« - 2 С*г. « 11 6 V---„ „ 12 о--" и 6 ^-----щель занрь <з-----Нещелевое Теоретик

>

А

А

У-,

—

/V

У

ч

“У

ima j ирьи φυβα.

У У

т

А

Sf у

А у

/а

у;

У ώ X1"

гч.

i

X

Г~

А

/у 1 у у

А

Ψ

А

и

4

ч

ч

^ А

/,

Й

У

V1

к-__

_ JV- -

>

;

А

щ

У J

S/s.

if

Ж

щ у

А: /у

ψΥ/, VV

и

ft

щ

у—

Уг

ол а

тан

у &У

I

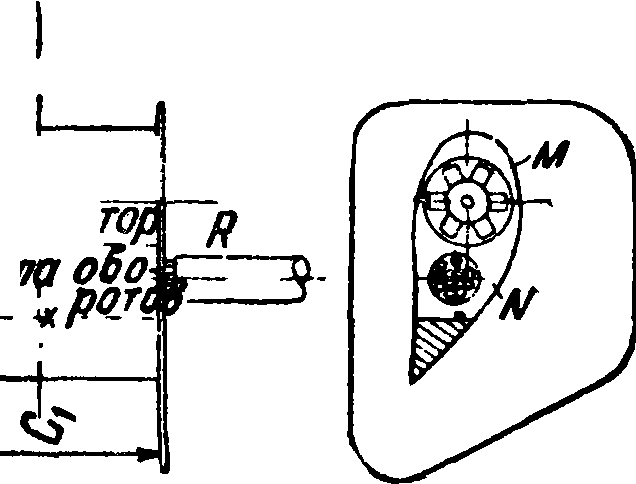
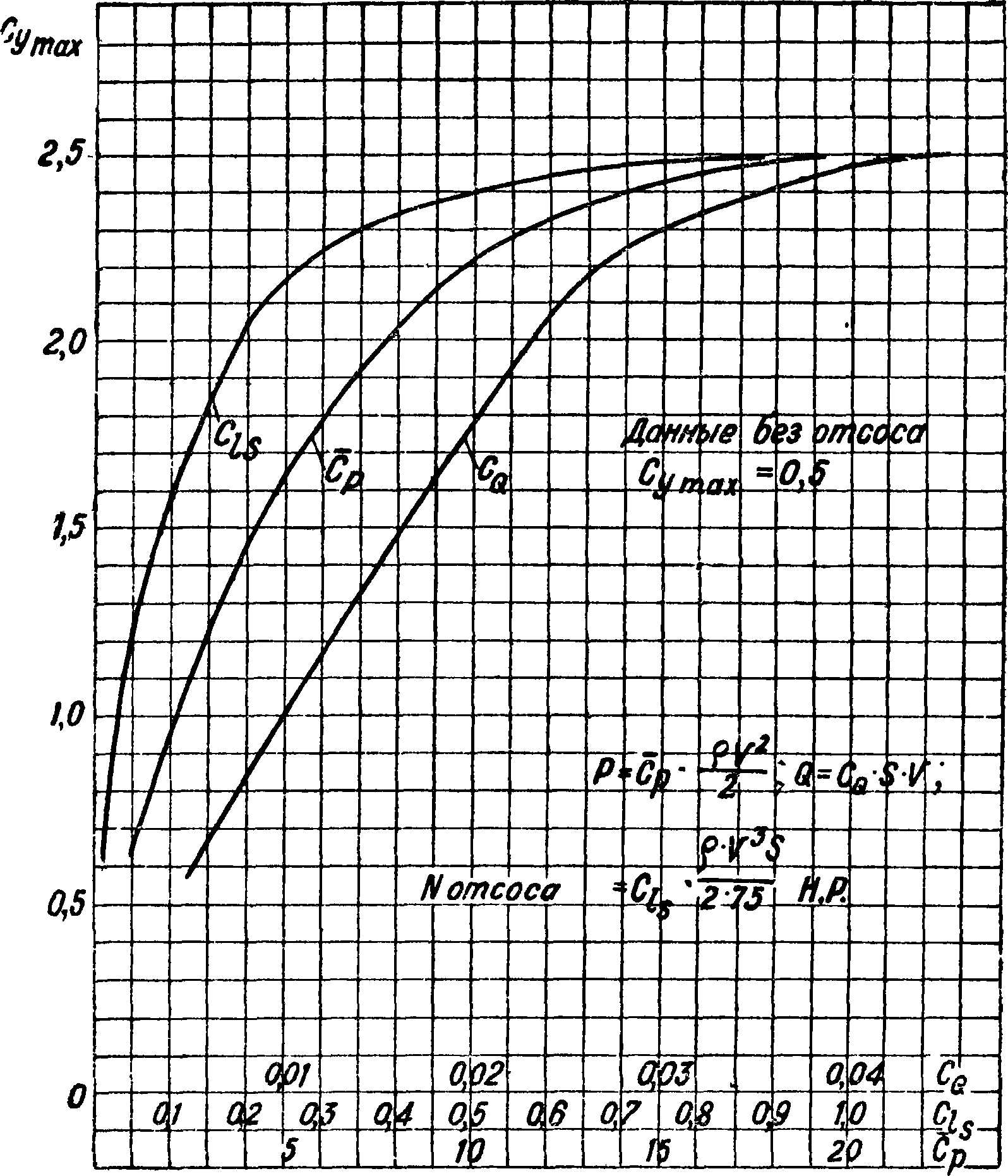
Для предотвращения срыва потока с крыла и увеличения С _шх можно производить отсасывание [⁸⁰, ⁸¹, ⁸². ⁸⁴ ] или сдувание [⁸¹, ⁸², ⁸³, ⁸⁴] пограничного слоя с верхней поверхности крыла. На фигуре 53 дан чертеж модели крыла, применявшейся в опытах с отсасыванием пограничного слоя, производившихся в большой трубе Геттингенской лаборатории [⁸⁰], а на фигуре 54 приведена зависимость Су max ^от безразмерных коэф-тов расхода, разрежения и мощности, потребной для отсасывания. Упомянутые безразмерные коэф-ты равны: коэф. расхода Cq=где Q — расход в m^z/ck, коэф. разрежения в камере С _р =, где р—величина разрежения в ка коэф. мощности С_г

где L_s—мощность, не-

12

Фигура 55.

24

28°

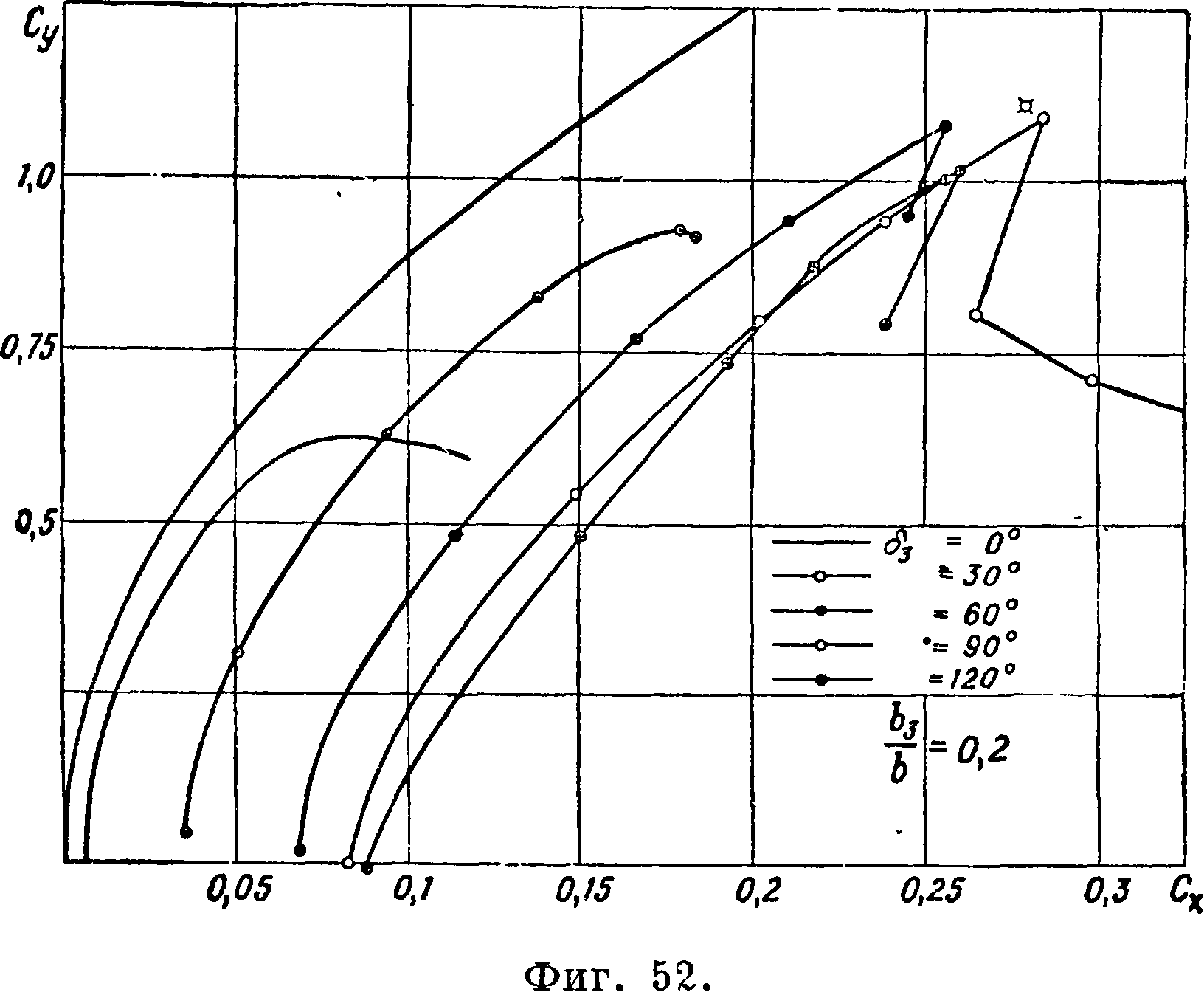
гнутости профиля. На фигуре 50 приведена диаграмма распределения давления по профилю крыла с предкрылком и закрылком [⁷⁴]; диаграмма дает соотношение между нагрузками, приходящимися

на каждый элемент разрезного крыла при С близком к максиму лгу. Разновидностью крыльев с закрылками являются крылья со щитками-закрылками. На фигуре 51 дан профиль крыла с таким закрылком, а на фигуре 52—поляры Лилиенталя при различных углах г5_? его отклонения при хорде щитка, равной 0,2 [⁷³]. Преимуществами крыла со щитком-закрылком являются: 1) отсутствие увеличения лобового сопротивления при <5^=0 по сравнению с сопротивлением исходного крыла и 2) увеличение подъемной силы при отклонении закрылка, сопровождающегося значительным увеличением лобового сопротивления (сравни фигура 49 и 52). Последнее обстоятельст мере, и

__ __

q S · V

обходимая для отсасывания с учетом потерь на выхлоп при условии отбрасывания струи воздуха назад (то есть с использованием реакции) и при условии равенства кпд винта и вентилятора. Фигура 54 позволяет определить необходимый расход, разрежение в камере и мощность установки в зависимости от С_{у пгах}. На фигуре 55 приведена зависимость С_у по а при различных С_рдля случая отсасывания и сдувания пограничного слоя через щель, расположенную на верх^ ней поверхности крыла [⁸²]. Опыты проводились при числе Рейнольдса Re=445 000 с крылом.

Фигура 57.

торцы которого примыкали вплотную к стенкам аэродинамич. трубы. Систематич. обработка этих опытов приводит к следующей формуле для определения приращения С _{и тах} в случае сдувания пограничного слоя

1,37 С,⁰⁴,

где коэф. С_г=С_р - Cq. Аналогичная ф-ла, найденная по опытам ЦАГИ и ВВА [⁸³], производив^

Т а

YOYN HidouQd mi иншчэо _____		<М -Ф	- 1
% увеличения диапазона скоростей	юоншчйнве шчхэойп э ошнэнавйэ оп	1	1
	шкифойп шчнДохэи о ошнэнавйэ оп	1	ха
% повышения подъемной силы	IMOH -шчйнве jwnxo -ойн э ошн -энавйэ оп	1	1
	иэи -ифойн шчн -Дохэи Э ошн -энавйэ оп	1	ха

₀ а Э1шэ иониэгйоп * 1мшэмтгг [ ndn вкифойп ojoh

-ДОХЭИ ИНВХВ ITOJX

^ЭКИЭИОГОМЭЧйОНИОН

-чшзшюмм ийп —

°0

л и VWfj ^

хтэхэойонэ ноетшви^

гшио ионшъДоп ’феон щчнчшзммнвн

ΒΙΓΗφΟίϊΠ охонДохэи хо % я T2HimclHT28 еМох

₀ а кгэкифосГи шчнДохэи и снчхэон -хс1эаоы иончкэхех -сшопэа κοχχ

АвтоматиЧ. предкрылок Хендлк-Пэдда *⁴ — _ 1,632*4, 114,2 _ 28 26 _ 345 _ 400

ЬН Jyi

cTgg о ” В о

S Й S. §Й«

g я

ogo

R И Η

bSS os g

»s

и ^H В к _m « в £ в

3“o gag, 3§g g“8 s _s о *go

D К W o»o m Mo n о Я g и Pi ft c °

к

Pi

к ей

И

3

Pi

к к

^Ч^’р

I

ей К л> О Р*5Г м

geo и §я « S

Н, К й

a a g

К

G5 о Н О

О*

К SB

<и

ft ·

В S о н л

(Ηϋβ

0 о b a ft в Й о F К И

о К Рн « m

1 о о К В В р В Ό ей О

«5 ^ и

^wgs

8"i

н ей К

|,“и

fgg

вё°

в в

SB

о «

К в Ϊ в * ·&

		Опечатка
Стр.	Строка	Напечатано	Должно быть	По чьей вине
129	5 графа по горизонт.	2,1 2	2,182	Типогр.

шимся при Re — 215 ООО и λ=2,5, имеет вид кС_{у тах}=1,225 Cg’⁴. Предел применимости обеих ф-лО С_е 0,15. На величину приращения С_утах

оказывают влияние относительный размах Я и высота концевых шайб. Эта зависимость еще не найдена. При вращении круглого цилиндра

Фигура 59.

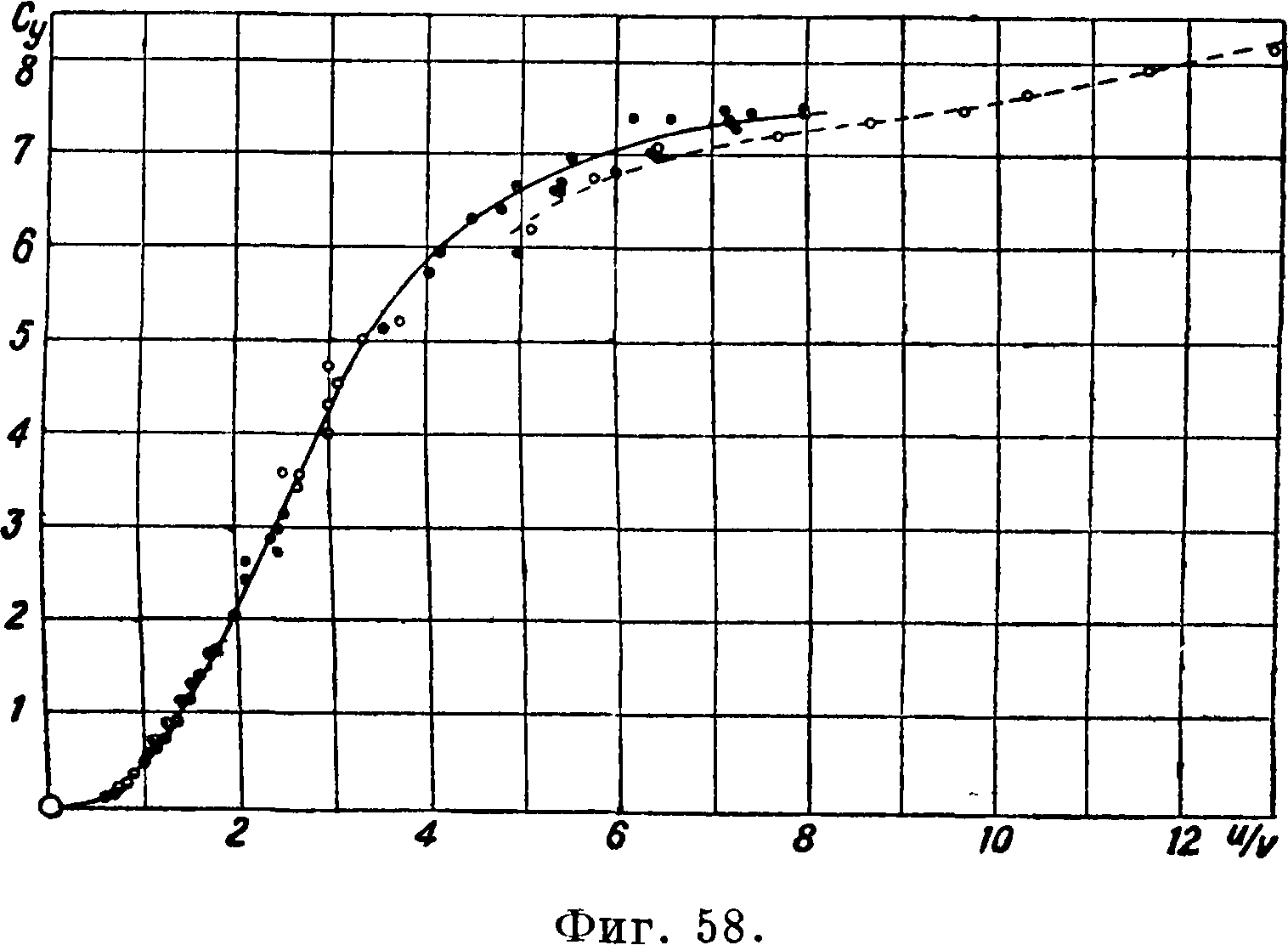
в потоке жидкости или газа возникает сила, перпендикулярная к набегающему потоку (эффект Магнуса). Это явление обусловливается возникновением циркуляции вокруг цилиндра, что видно из рассмотрения фигура 56 и 57. На фигуре 56 приведен спектр обтекания невращающегося цилиндра, а на фигуре 57 — спектр обтекания вращающегося цилиндра при ~=6, где и — окружная скорость вращения Цилиндра. На фигуре 58—60 даны результаты опытов, проведенных в Геттингенской лаборатории [⁸⁵]. Из рассмотрения фигура 58—60 видно, что подъемная сила и лобовое сопротивление вращающегося цилиндра зависят от отношения скоростей и размеров концевых шайб. Значения С_у мх У вращаю-Ф_ИГ# go. щихся цилиндров весь ма велики. Вращающиеся цилиндры еще не нашли .практич. применения на самолетах вследствие большого лобового сопротивления и опасности аварии при остановке мотора. Были попытки [⁸⁸] уменьшить лобовое сопротивление путем установки обтекателей, однако в этом случае С_{у тах} цилиндра уменьшается.

Лит.: 1) Dry den Н. a. Kuethe A., The Measurement of Fluctuations of Air Speed by the Hot-Wire Ane

mometer, «Technical Report NACA», Wsh., 320; 2) Uber den Reibungswiderstand stromender Luft, «Ergebnisse der Aerodynamischen Yersuchsanstalt zu Gottingen», Mch. — B., 1927, Lfg 3; 3) Zur turbulenten Stromung in Rohren und langs Platten, ibid., 1932, Lfg 4; 4) Karma n Th., Turbulence a. Skin Friction, «Journal of the Aeronautical Sciences», 1934, v. 1, 1; 5) Кожевников А., Сравнительные испытания одного и того же металлич. крыла и шара в аэродинамич. трубах СССР и за границей, «Труды Первой всесоюзной конференции по аэродинамике», 1931, 1932,- 6) D г у d е η Н. а. Кие“ the A., Effect of Turbulence in Wind Tunnel Measurements, «Technical Report NACA», Wsh., 342; ?) Mi 1 likan C. a. Klein A., The Effect of Turbulence, «Aircraft Engineering», L., 1933, August; 8) Flachsbart O., Der Widerstand von Kugeln in d. Umgebung der kriti-schen Reynoldsschen Zahl, «Ergebnisse der Aerodynamischen Yersuchsanstalt zu Gottingen», Mch.—B., 1927, Lfg 4; ⁹) Versuche uber den Luftwiderstand gerundeter u. kan-tiger Korper, ibid., 1929, Lfg 2, 2 Aufl.; W) H i 1 d a M. L у о n, Effect of Turbulence on Drag of Airship Models, «Aeronautical Research Committee, Rep. a. Mem.», 1511; ⁿ) Versuche uber den Luftwiderstand gerundeter u. kan-tiger Korper, «Ergebnisse der Aerodynamischen Yersuchsanstalt zu Gottingen, 2 Aufl., Mch.—B., 1929, Lfg 2; i²) F a g e A. a. F a 1 k n e г V., The Flow around a Circular Cylinder, «Aeronautical «Research Committee, Rep. a. Mem.», 1369; 13) Stack J., Tests in the Variable-Density Wind Tunnel to Investigate the Effects of Scale a. Turbulence on Airfoil Characteristics, «Technical Note NACA», Wsh., 364; 14) Атлас профилей, «Труды ЦАГИ», Μ., 1931, вып. 99; 15) Munk М., Determination of the Angles of Attack of Zero Lift a. of Zero Moment, Based on Mink’s Integrals, «Technical Note NACA», 122; 16) г л а с e Ф., Исследование профильного сопротивления крыльев, «Техника воздушного флота», М., 1929, 1; i?) Rauhigkeitseinflusse an Tragflugeln, «Ergebnisse der Aerodynamischen Versuchsanstalt zu Gottingen, Mch.—В., 1927, Lfg 1 u. 3; 18) Jacobs E., Airfoil Section Characteristic as Affected by Protuberances, «Technical Report NACA», Wsh., 446; Щ Hooker, The Aerodynamic Characteristics of Airfoils as Affected by Surface Roughness, ibid., 457; 20) Schrenk M., Gher Profil-widerstandsmessung im Fluge nach dem Impulsverfah-. ren, «Deutsche Yersuchsanstalt f. Luftfahrt», 102, B.—Ad-lerhof, 1929; ²i) Оглоблин А., Систематич. исследования крыльев, «Труды ЦАГИ», М., 1933, вып. 145; 22) Красильщиков И., О зависимости между некоторыми геометрич. параметрами профиля и его аэродинамич. характеристиками, «Труды ЦАГИ», М., 1932, вып. 103; 23) J а с о b s E., W a r d К. a. Pinkerton R., The Characteristics of 78 Related Airfoil Sections from Tests in the Variable-Density Wind Tunnel, «Technical Report NACA», Wsh., 460; 24) Munk M., General Theory of Thin Wing Sections, «Technical Report NACA», Wsh., 142; 25) Glauert H., A Theory of Thin Airfoils, «Aeronautical Research Committee, Rep. a. Mem.», 910; 26) B i r n b a u m, Die tragende Wirbelflache als Hilfs-mittel zur Behandlung des ebenen Problems der Trag-flugeltheorie, «Ztschr. f. angew. Mathematik u. Mecha-nik», B., 1923; 27) г л а у э p т Г., Основы теории крыльев и винта, пер. с англ., М., 1931; 28) Гласс Ф., О влиянии рейнольдсова числа на величину максимальной подъемной силы, «Труды ЦАГИ», М., 1932, вып. 103; 29) j а-с о b s Е., The Aerodynamic Characteristics of Eight Very Thick Airfoils from Tests in the Variable-Density Wind Tunnel, «Technical Report NACA», Wsh., 391; 30) T a p г С., О влиянии крыла на продольную статич. устойчивость самолета, «Техника воздушного флота», М., 1933, 9; 31) Arsandaux L., Etude, calcul et determination de certaines formes d’ailes dvolutives le long de Tcnvergure, «L’A£ronautique», P., 1928, 106, 107; 32) Голубев В., Теория крыла аэроплана конечного размаха, «Труды ЦАГИ», М., 1931, вып. 108; 33) ю р ь-е в Б., Индуктивное сопротивление крыльев аэроплана, там же, 1926, вып. 20; 34) О с т о с л а в с к и и И., Новый метод аэродинамич. расчета бипланной коробки, «Техника воздушного флота», М., 1931, 12; 35) Sherman A., The Aerodynamic Effects of Wing Cut-outs, «Technical Report NACA», Wsh., 1934, 480; зв) ч e с а-л о в А., Построение поляры Лилиенталя монопланного крыла произвольной формы, «Труды ЦАГИ», М., 1929, вып. 42; 37) Победоносцев Ю., Графич. метод построения циркуляции по размаху, там же, 1929, вып. 42; 38) G a r г i k, Determination of the Theoretical Pressure Distribution for Twenty Airfoils, «Technical Report NACA», Wsh., 465: 39) l 0 t z I., Berechnung d. Auftriebs-verteilung beliebig geformter Fliigel, «ZFM», 1931, 7; 40) H u e b e r J., Die aerodynamischen Eigenschaften von doppeltrapezf6rmigen Tragflugeln, ibid., 1933, 9,

10; 4i) H u e b e r J., Der verwundene Tragfliigel, ibid., 11; 42) p r a n d t 1 L., Gber Tragfliigel kleinsten induzier-ten Widerstandes, ibid., 1933, 11; «) Беляев В, Аэродинамич. теория закрученного крыла, «Техника воздушного флота», 1933, 2; 44) Higgins G., The Prediction of Airfoil Characteristics, «Technical Report NACA», Wsh., 312; 45) Muller H., Fliigelschnitt u. Fluglei-stungen, «Luftfahrforschung», 1929, В. 5, Η. 1; 4β) T ο u s-saint A., L’Aviation actuelle, Etude a^rodynamique

et essais des avions, «L’Aviation actuelle et la s6curit6», P., 1928; 47) Theodorsen T._f On the Theory of Wing Sections with Particular Reference to the Lift Distribution, «Technical Report NACA», Wsh., 383; 48) The o-dorsen T., Theory of Wing Sections of Arbitrary Shape, ibid., 1931, 411; 49) Theodorsen T. a. О a r r i c J., General Potential Theory of Arbitrary Wing Sections, ibid., 452; 50) Юрьев Б. и Лесникова H., Аэро-динамич. исследования, «Труды ЦАГИ», 1928, вып. 53; 51) Ширманов П., Устойчивость пути изолированного крыла. Круговая обдувка крыльев, там же, 1928, вып. 36; ⁵²) Мартынов А., Исследование работы оперения самолета методом распределения давления, там же, М., 1933, вып. 163; 53) Род Р., Распределение давления по крыльям и хвостовому оперению истребителя PW-9 в полете, «Технич. заметки ИНФО ЦАГИ», 1933, 5; 54) Messung d. Druekverteilung an drei Eindecker-flachen u. an einem Doppeldecker, «Ergebnisse d. Aero-dvnamischen Yersuchsanstalt zu Gottingen», 2 Aufl., Mch.—B., 1929, Lfg 2; 55) N о r t ο n F. а. В a c ο n D., Pressure Distribution over the’Thick Airfoils Model Tests, «Technical Report NACA», Wsh., 1922, 150; 56) j _a с о b s E. a. Pinkerton R., Pressure Distribution over a Simmetrical Airfoil Section with Trailing Edge Flap, ibid., <360; 57) w i e s e 1 s b e r g e r C., Bestimmung der durch die Querruderwirkung beim Tragflugel erzeug-ten Luftkrafte u. Momente, «ZFM», 1928, 13; 58) w i e-selsberger C., Theoretische Untersuchungen uber die Querruderwirkung beim Tragflugel, «Report of the Aeronaut. Research Institute Tokyo Imperial University», 1927, <30; 59) Жуковский H., О поддерживающих планах типа «Антуанетт», «Труды Отд. физ. наук общества любителей естествознания», 1911, т. 15, вып. 2; 60) Чаплыгин С., К общей теории крыла моноплана, М., 1922; βΐ) Голубев В., Теория крыла аэроплана в плоско-параллельном потоке, «Труды ЦАГИ», М., 1927, вып. 29; 62) Aerodynamic Characteristics of Airfoils, «Technical Report NACA», Wsh., 93,124,182, 244, 286, 315; 63) 3 а с о b s E., Large Scale Aerodynamic Characteristics of Airfoils as Tested in the Variable-Density Wind Tunnel, ibid., 1930, 352; 64) Fliigelprofiluntersu-ebungen, «Ergebnisse der Aerodynamischen Versuchsan-stalt zu GrOttingen», Mch.—B., 1927—32, Lfg 1, 3, 4; 65) Toussaint A. et Carafoli E., Theorie et Traces des Profils d’ailes sustentatrices, P., 1928; 66) Carafoli E., A6rodynamique des ailes d’avions, theorie et applications, «Revue g£n£ral de Fa6ronautique», P., 1929, 10; 67) Красильщиков П., Практич. применения разрезных крыльев, «Техника воздушного флота», М., 1932, 5—6; 68) е г о ж е, Исследования по разрезным крыльям с закрылком, «Труды ЦАГИ», М., 1931, вып. 105; 69) е г о ж е, Влияние длины закрылка и ппед-крылка на работу разрезного крыла, там же, М., 1932, вып. 133; 70) _е г о ж е, О выборе наивыгоднейшего положения предкрылка, там же, М., 1933, вып. 161; 71) Т о w-nend Н., A Study of Slots, Rings a.

Boundary Layer Control by Blowing, «The Journal of the Royal Aeronautical Society»,

L., 1931, 8; 72) w e n z i n g e r C. a. S h о r-t a 1 J., The Aerodynamic Characteristics of a Slotted Clark-Y Wing as Affected by the Auxiliary Airfoil Position, «Technical Report NACA», Wsh., 400; 73) Ушаков Б., Аэро-динамич. исследования автоматич. предкрылка, «Технич. заметки ИНФО ЦАГИ», М.,

1932, вып. 2; 74) G-ruschwitz Е. и.

Schrenk О., tlber eine einfache M6glich-keit zur Auftriebserhohung von Tragfliigeln,

«ZFM», 1932, 20; 75) г о л у б е в В., Исследования по теории‘разрезного крыла, «Труды ЦАГИ», М., 1933, вып. 147; 76)Lachmann

G., Control beyond the Stall, «The Journ. of the Royal Aeronautical Society», L., 1932,

256; 77) Ушаков Б., Влияние размеров предкрылка на работу разрезного крыла,

«Технич. заметки ИНФО ЦАГИ», М., 1932,

2; 78) его же, Влияние исходного профиля на работу предкрылка, там же, М., 1932,

22; 79) S с h r e h к О., Versuche mit einem Absaugeflugel, «ZFM», 1931,.9;⁸⁰)Perring W. a. Douglas О., Wind Tunnel Experiments on -the Effect of the Maximum Lift of Withdrawing a. Discharging Air from the Upper Surface of an Airfoil, «Aeronautical Research Committee, Rep. a. Mem.», 7700; si)

Millard J. Bamber, Wind Tunnel Tests on Airfoil boundary Layer Control Using a Backward-opening Slot, «Technical Report NACA», Wsh., 385; 82) з а к с Результаты предварительных опытов со сдуванием пограничного слоя, «Труды 3 Всесоюзной конференции но аэродинамике», М., 1932; 83) Красильщиков П., Улучшение аэродинамич. свойств крыла путем отсасывания и сдувания пограничного слоя, «Технич. заметки ИНФО ЦАГИ», 1932, 6; 84) Messungen an rotierenden Zylindern, Ergebnisse der Aerodynamischen Versuehs-anstalt zu Gottingen, Mch.—B., 1932, Lfg 4; 85) Wo life

H. en Koning C., Vorgezet onderzoek naar den in-

vloed van een draaiende rol, aangebracht in een vleugel-profil, Verh. Rijks Studiedienst v. d. Luchvaart, Amsterdam, 1925, Deal 3, p. 47. П. Красильщиков.

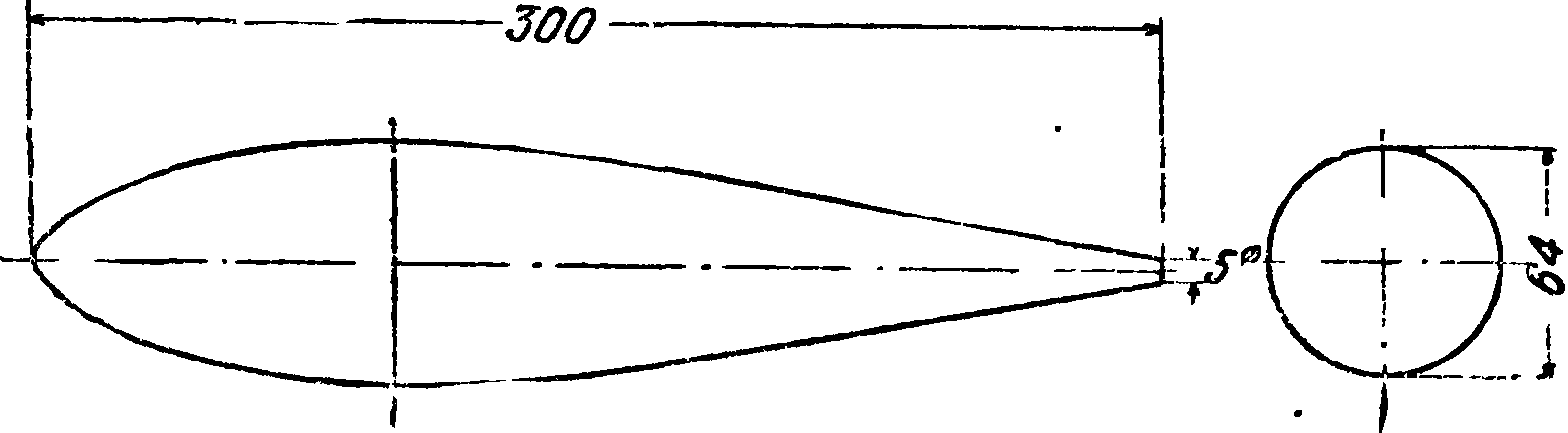
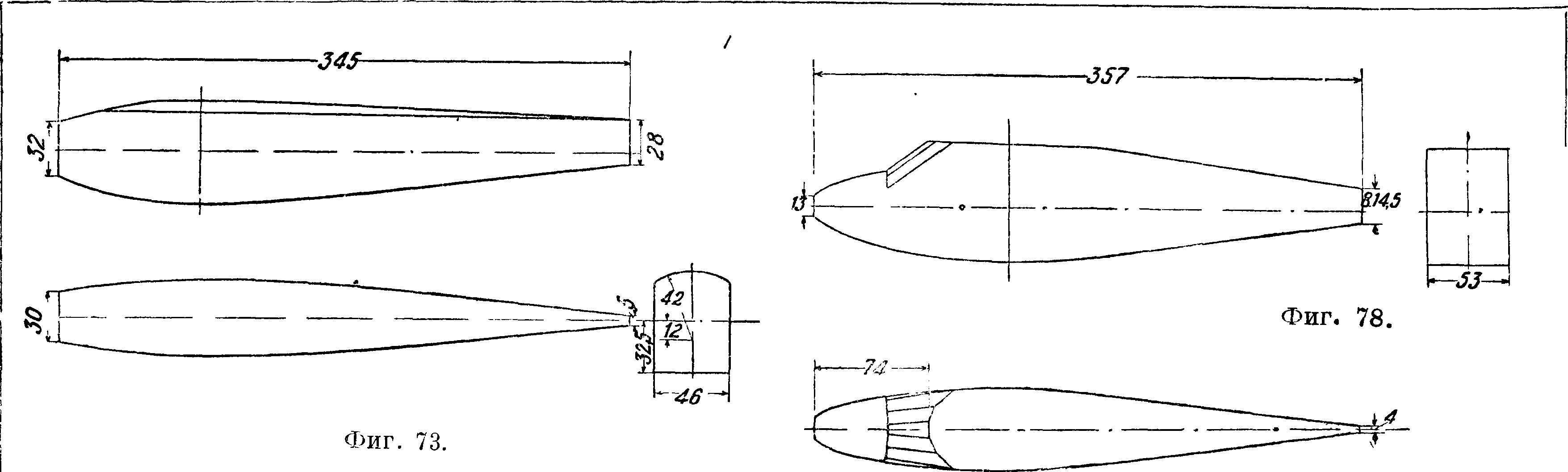
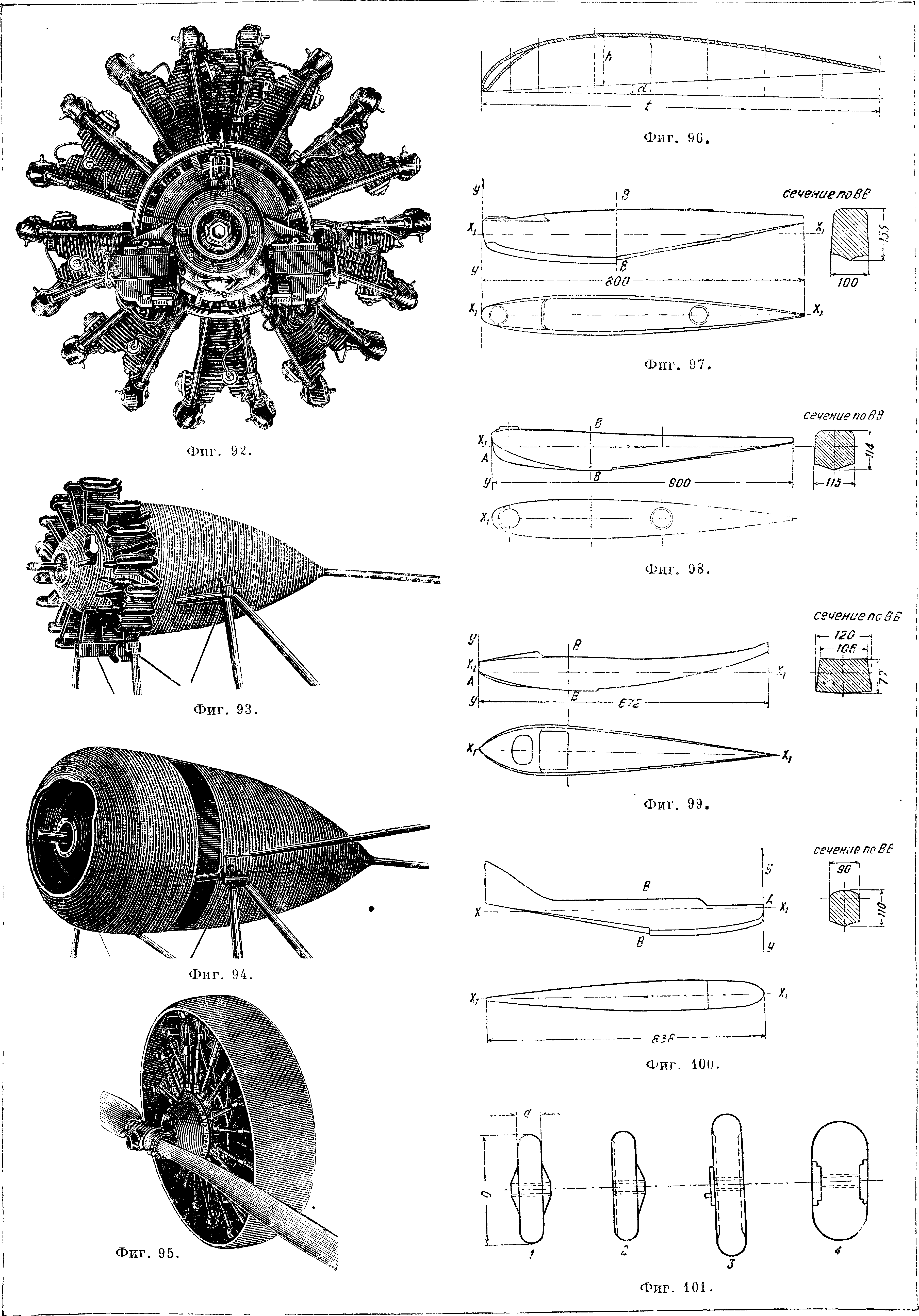
VIII. Профили винтов, а) Профили RAF-6 (английские). Для деревянных винтов одними из лучших являются английские винтовые профили RAF-6. Очертания этих профилей даны на фигуре 61, а ординаты—в табл. 5. Аэродинамич.

Фигура 61.

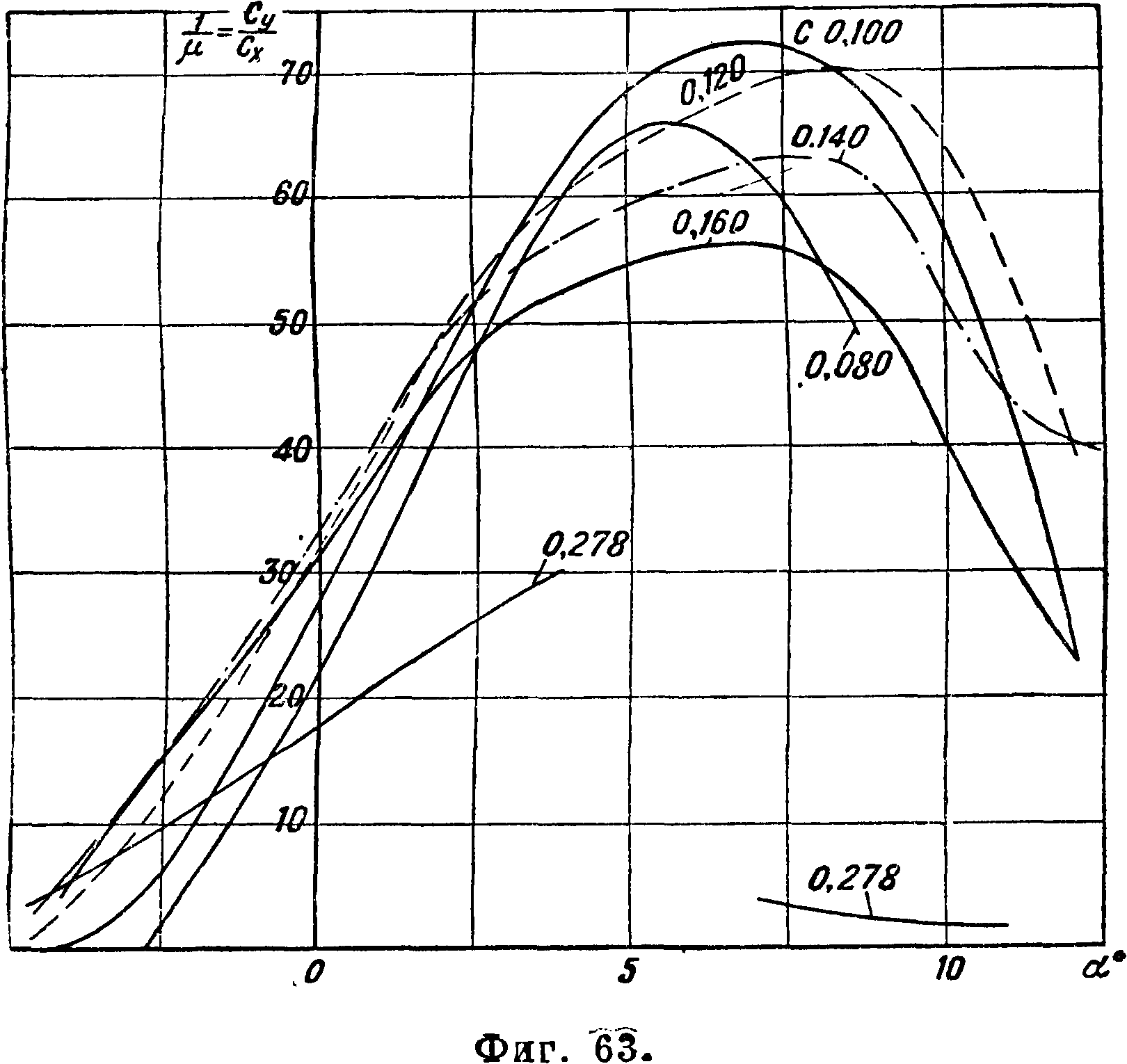
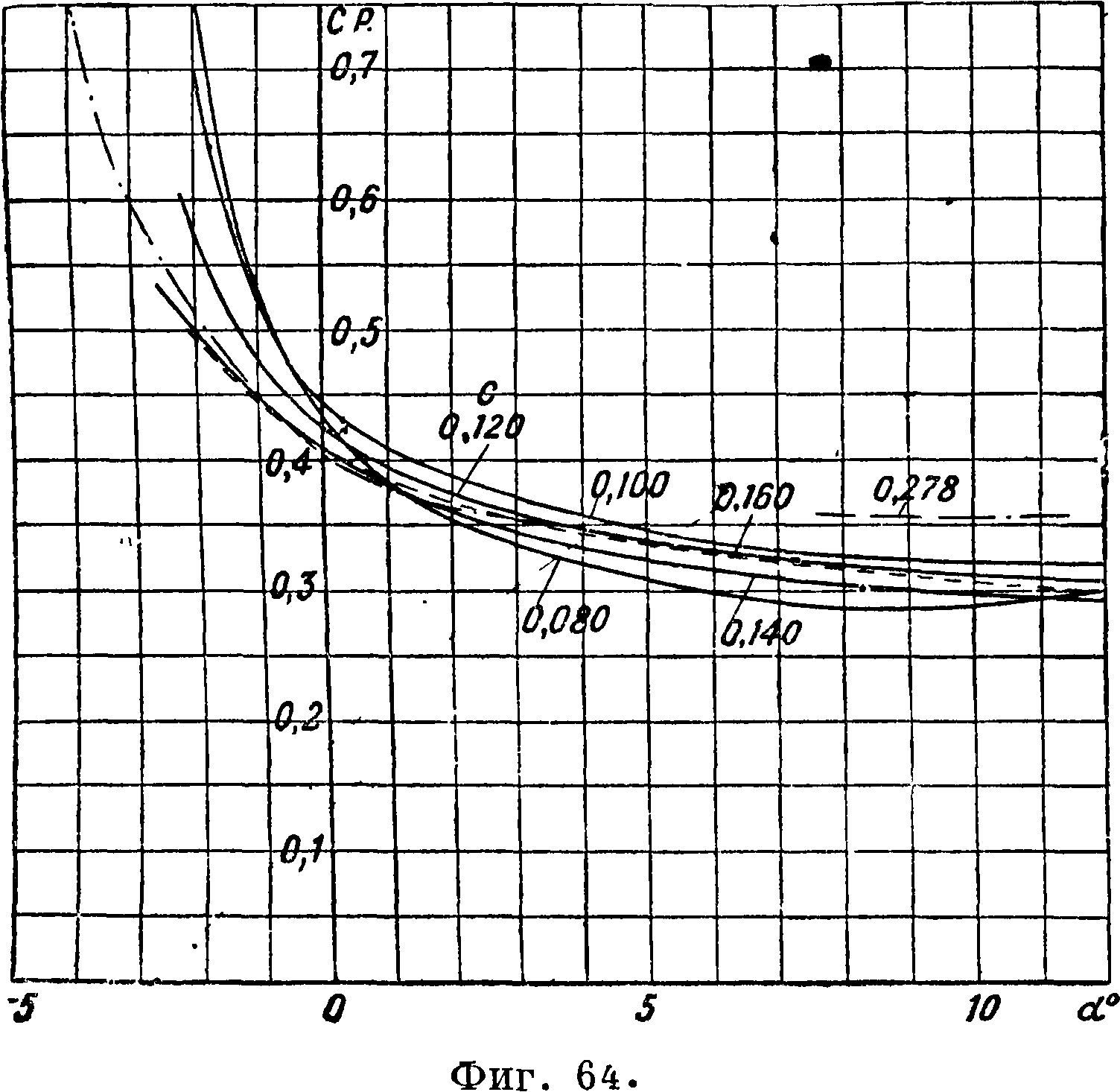
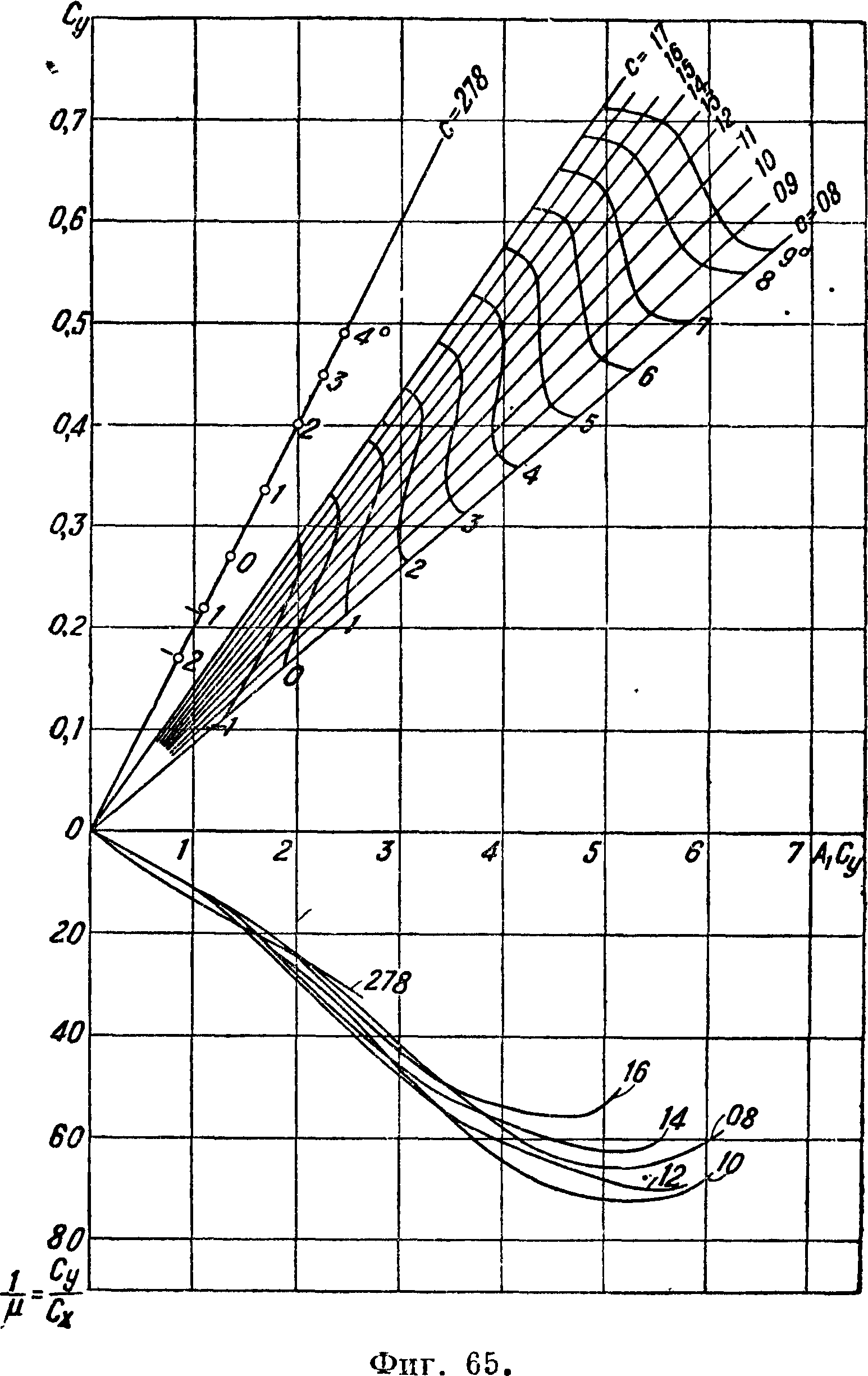
характеристики этих профилей,· приводимые на фигуре 62, 63 и 64, получены интерполированием данных испытаний серий крыльев относительной толщины с=0,086; 0,103; 0,129; 0,168 и крыла с выпуклой нижней поверхностью относительной толщины с=0,278, пересчитанных на бесконечный размах по ф-лам для прямоугольных крыльев с учетом падения циркуляции к концам за счет большего скоса потока у концов и увеличения вследствие этого к концам индуктивного сопротивления. Относительный размах крыльев при испытании был равен 6 при хорде 159 миллиметров. Скорость потока равнялась ~ 24 м]ск. В табл. 6 даны ф-лы для определения положения ц. т., площади, моментов инерции и модулей сопротивления профилей. Все перечисленные

S О 5 10 сС°

Фигура 62.

! Профиль	Расстояние от носика в % хорды		2,5	5	10	20	30	40	50	60	70	80	90	Радиусы
														носика	хвостика
RAF-6*	Ординаты в % максимальной толщины	Ув	41,1	59,2	78,6	96,1	100,0	99,1	96,1	87,3	74у7	57,2	36,9	12,0	9,0
ВС-2		Ув	18,9	30,4	46,2	65,2	72,6	73,7	70,6	63,3	52,8	40,0	24,2	1 8,0	8,0
		Ун	12,1	16,7	21,9	25,9	25,9	28,5	20,8	18 Д	15,4	12,7	10,0

* Ординаты двояковыпуклого толстого профиля с относительной толщиной с=0,278 даны на фигуре 61.

величины выражены в ф-ии толщины профиля δ и его хорды b. На фигуре 65 представлена диаграмма, служащая для подбора сечений лопасти

винта, с учетом одновременно условий прочности и условий А.; на этой диаграмме по оси абсцисс отложены произведения коэф-та модуля со

противления изгибу для растянутых волокон на коэф. подъемной силы профиля А_гС_у, а по оси ординат — коэф. подъемной силы С_у. На этой же фигуре внизу приведены кривые качества про-

Ф^илей 7=§?

Ь) Профили ВС-2. Для быстроходных винтов (преимущественно металлических) более выгодными являются профили ВС-2 и Clark-Y, мал© отличающиеся друг от друга. Очертания профиля ВС-2 даны на фигуре 66, а ординаты в таблице 5. Аэродинамич. _{Фиг> 66}

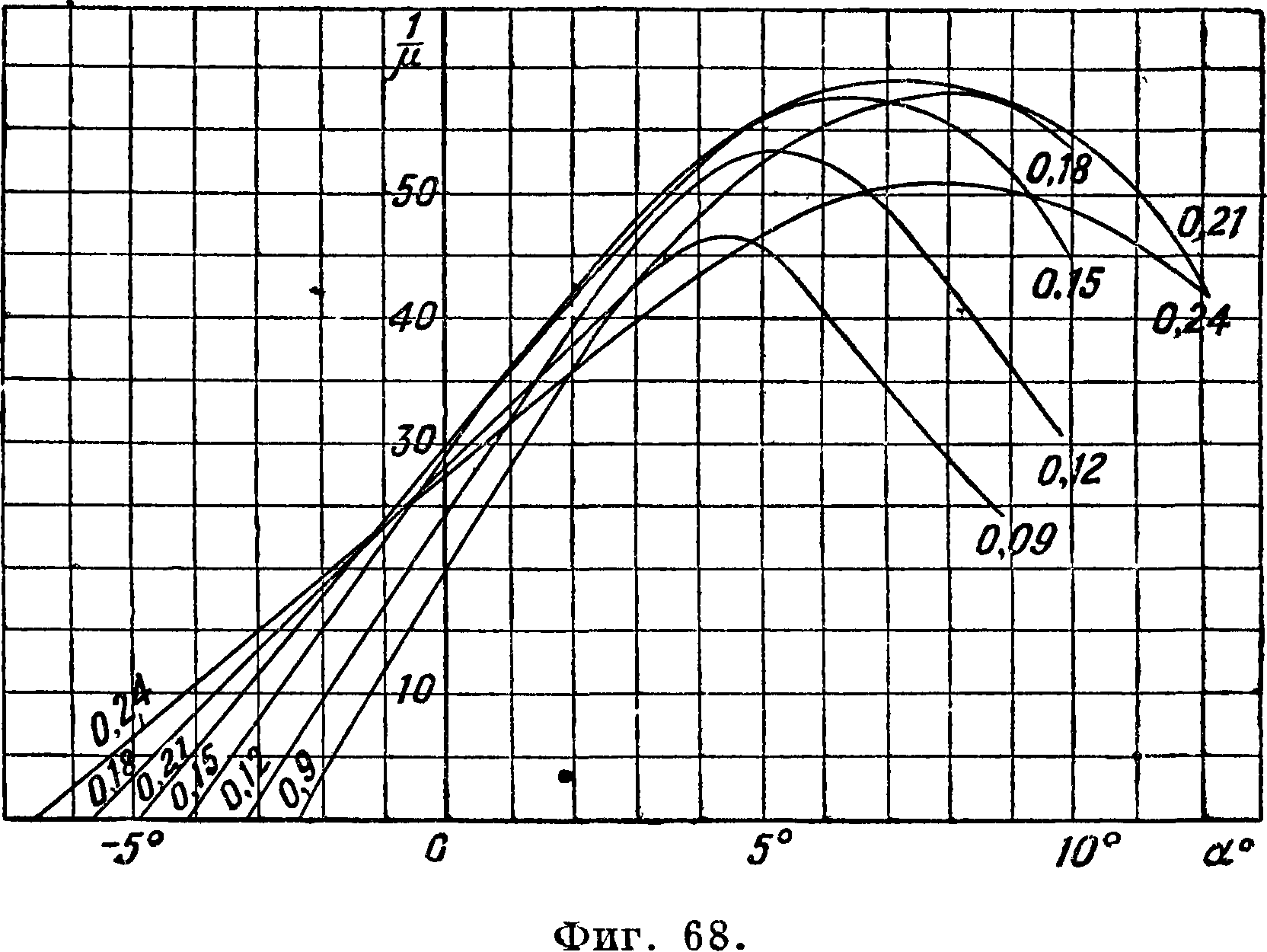
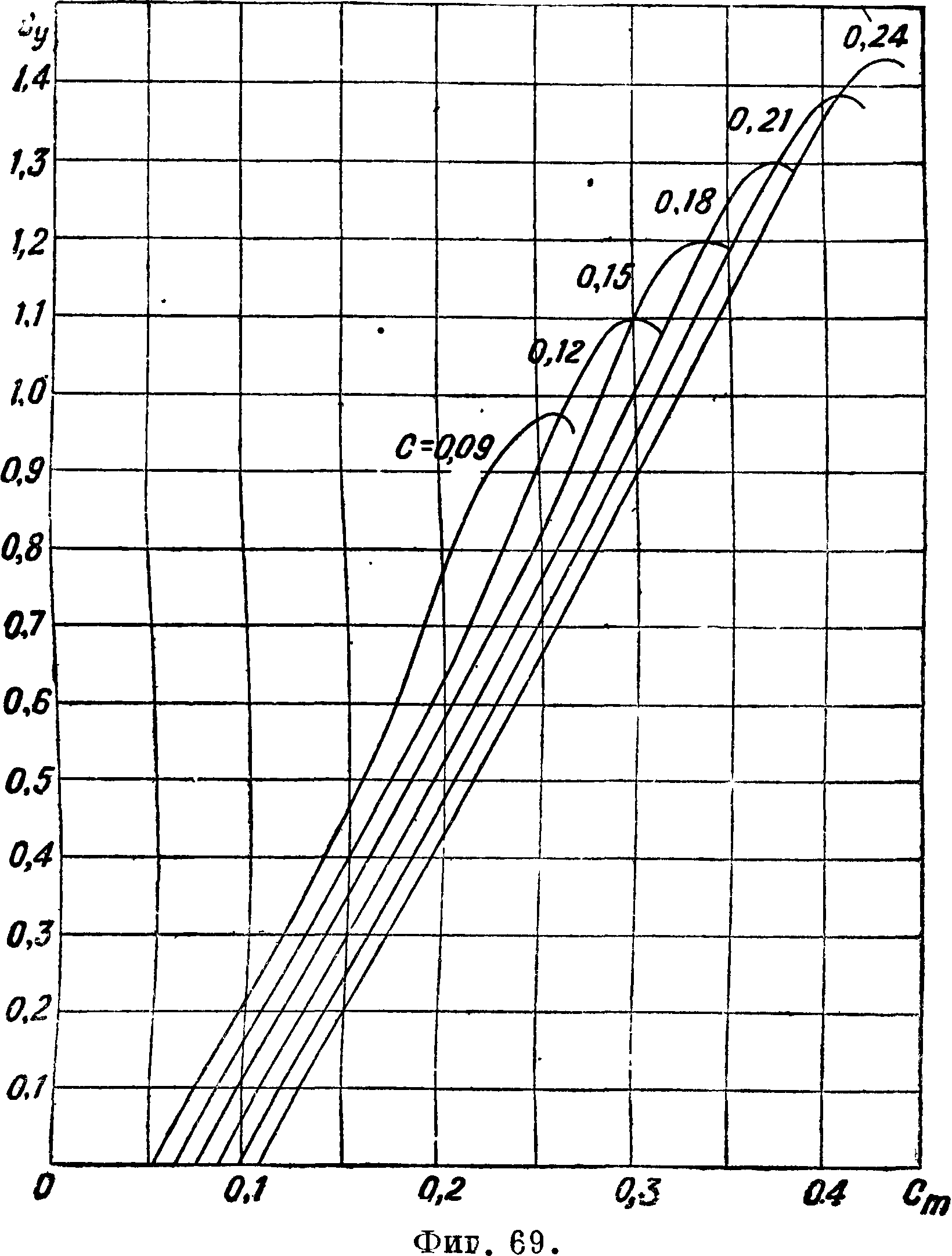
характеристики профилей серии ВС-2, полученные путем обработки и пересчета на бесконечный размах результатов испытаний крыльев относительной толщины с=0,09; 0,10; 0,12; 0,15; 0,18; 0,20; 0,21 и 0,24, представлены на фигуре 67, 68, 69. Относительный размах дужек при испытании был равен 5 при хорде 150 миллиметров. Испытания производились в трубе НК-1 ЗАО

Т а б л. 6.— Формулы для определения центра тяжести, площади, моментов инерции и модулей сопротивления профилей RAF-6 и ВС-2.

Название величины

Хорда

Максимальная толщина

Относительная толщина“

Площадь сечения

Расстояние ц. т. от носика..· · · ·

Расстояние ц. т. от хорды

Момент инерции относительно оси, проходящей через ц. т. и параллельной хорде..

Момент инерции относительно оси, проходящей через ц. т. и перпендикулярной хорде..

Центробежный момент инерции относительно осей х, у. Угол оси наименьшей жесткости с хордой:

a) в радианах

b) в градусах

Моменты инерции относительно осей эллипса инерции:

а) наименьшийг

b) наибольший

Расстояние до наиболее удаленных от главной оси инерции волокон:

a) до верхнего сжатого волокна..

b) до нижнего растянутого волокна..

Модули сопротивления на изгиб относительно главной оси инерции:

а) для верхних сжатых волокон..

Ь) для нижних растянутых волокон..

Коэф-ты модуля сопротивления изгибу относительно главной оси инерции:

а) для верхних сжатых волокон ..

Ь) для нижних растянутых волокон

_Про

RAF-6

Ь

6

б

^С~~ b s=0,750b х₀=0,445Ь Уо=0,420

I_x=0,053<33b К,=0,047<5ЬЗ

1_Ху=0,009<32Ь2

0=0,195с 6°=11,2с

°’^05Шb=Ж6

до

!= 0,048*3=—

»72=0,586 η_Λ=0,506

W t=—=0,08862b It

_w __ —1- — 0,10262b

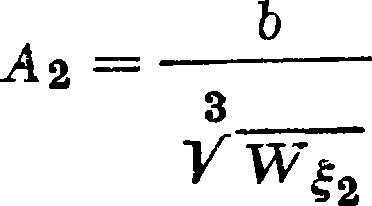
2,25

3

V~&

Ai =

b

3 _

Vw_h

2,14 3 _ Yc²

BC-2

b

6

6

5=0,7056b xo=0,448b Vo=0Д956

I_x=0,042363b

I=0,04106b* I_xy=0,0013962b²

6=0,035c $· — 2c

Ijt=0,042363b=—

* 2o,0

653

I_n=0,04106b» *= —

ч 24,4

«=0,5456 r/J=0,4556

. 0,077762b

Wt₁=—=0,093062b A2 =

%

b

2,34

Ai=-

b_

3 _

VW*.

3 _

V & 2,21 3 _

V &

ЦАГЙ при скорости потока ~ 30 м/ск. Ф-лы для определения положения ц. т., площади,

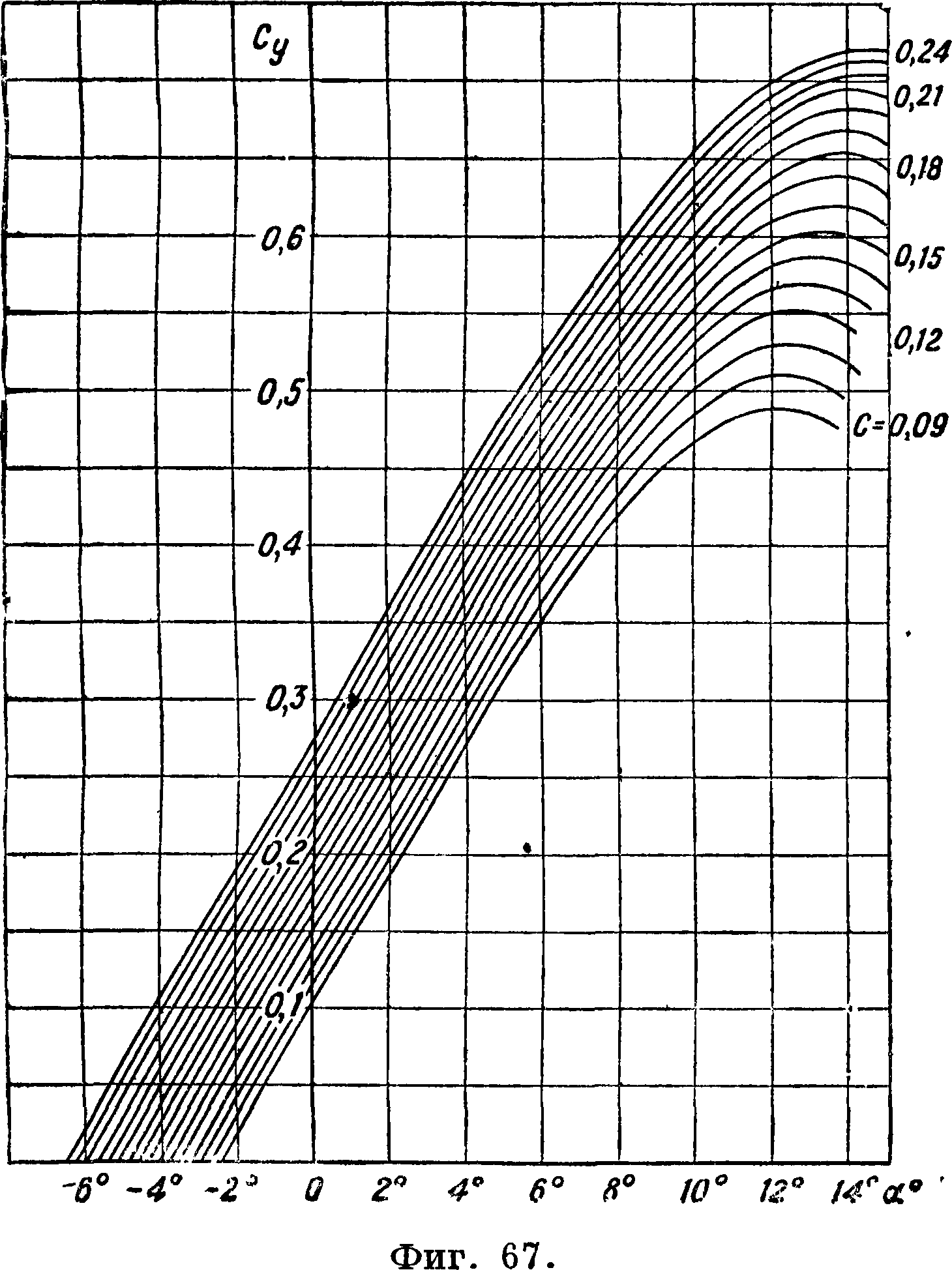
моментов инерции и модулей сопротивления профилей для серии ВС-2 представлены в таблице 6. Диаграмма, служащая для подбора сечений лопасти винта с профилями ВС-2, представлена на фигуре 70. При проектировании винтов с профилями Clark-Y можно приближенно пользоваться характеристиками профилей ВС-2.

Лит.: Кузьмин Г., Диаграммы для проектирования воздушных винтов, «Труды ЦАГИ», 1929, вып. 38; Кузьмин Г. и Халезов Д., Диаграммы для проектирования воздушных винтов с профилями ВС-2, «Труды ЦАГИ», 1933, вып. 137; Кузьмин Г., Расчет винта по вихревой теории, «Труды ЦАГИ», 1932, вып. 132; Лесникова Н., Графики для расчета гребных винтов, М.—Л., 1932. Д. Халезов.

IX. ЛоСозые сопротивления частей самолета.

1. Аэродинамические характеристики изолированных дета-I лей. а) Аэродинамические х а р а к-

теристики фюзеляжей, моторных гондол, лодок и поплавков. Про-

А

Ж

к.

/У

1

ψ

h-

а

%

L.

2

£

v

ш

£

• V

т

А

XX

X”

§

0

9

А

i

i

//А V

%

>>

А

1

УХ/

* ύ

j

А//Л

У2

(1 ~

*

f

έ

2

3

4

5

>

у

00

>

%

i

24,

£О.К

_—1

//j

а/5 0.18

21

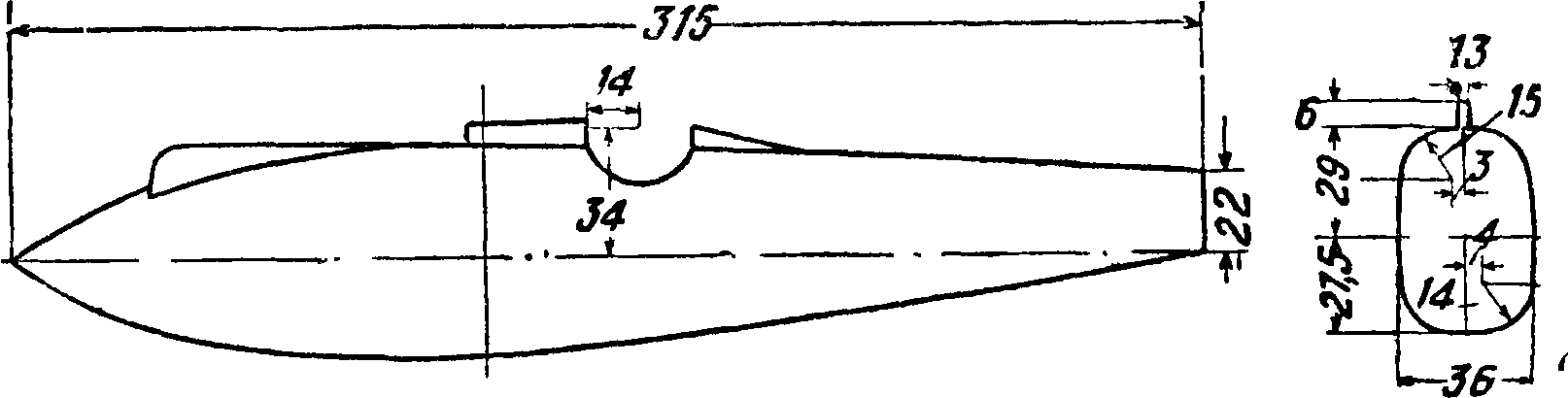
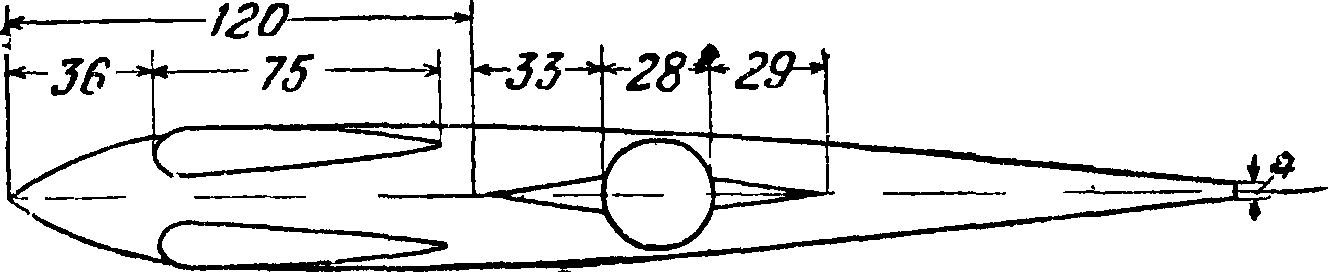
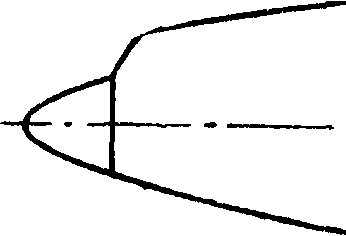
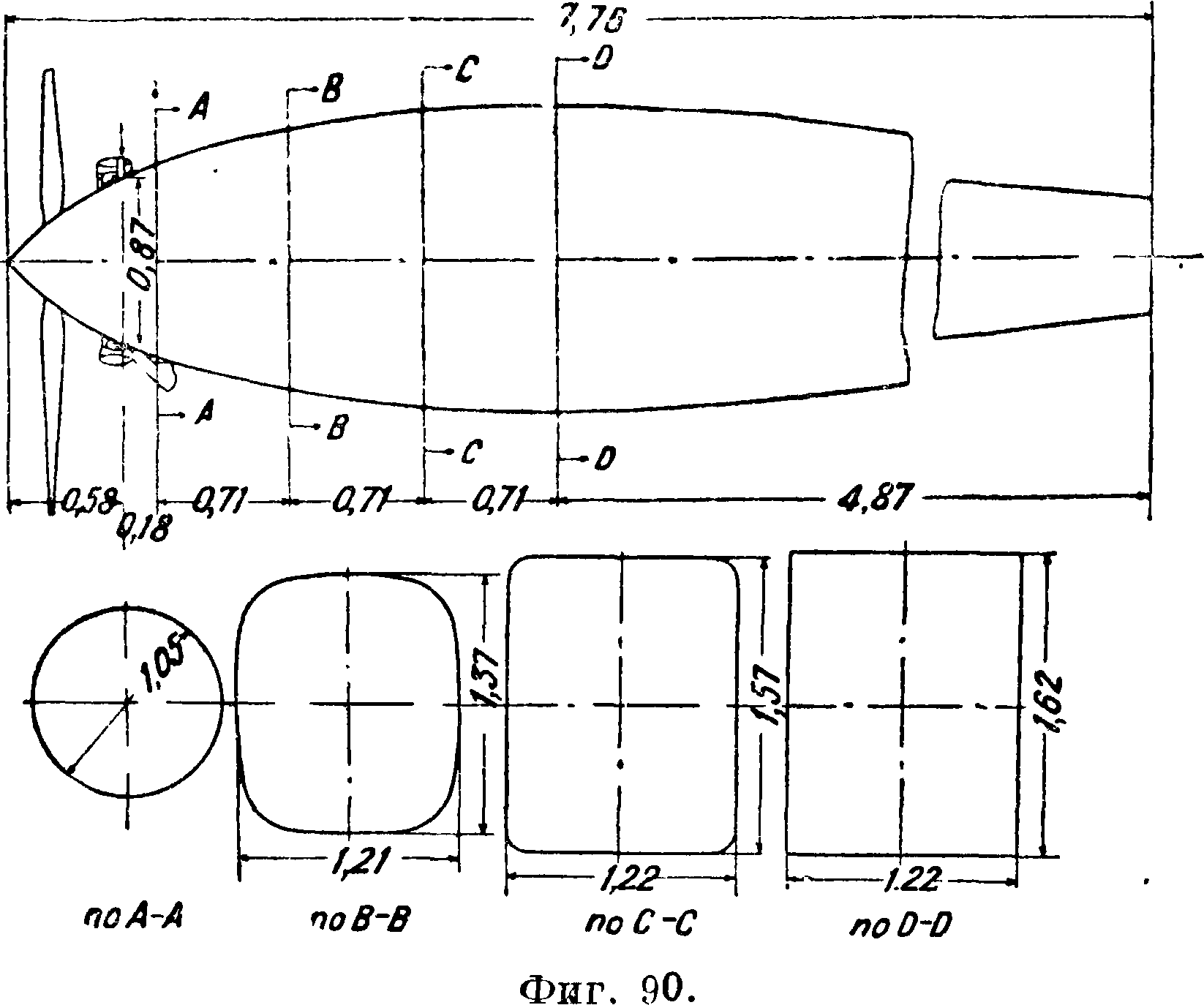
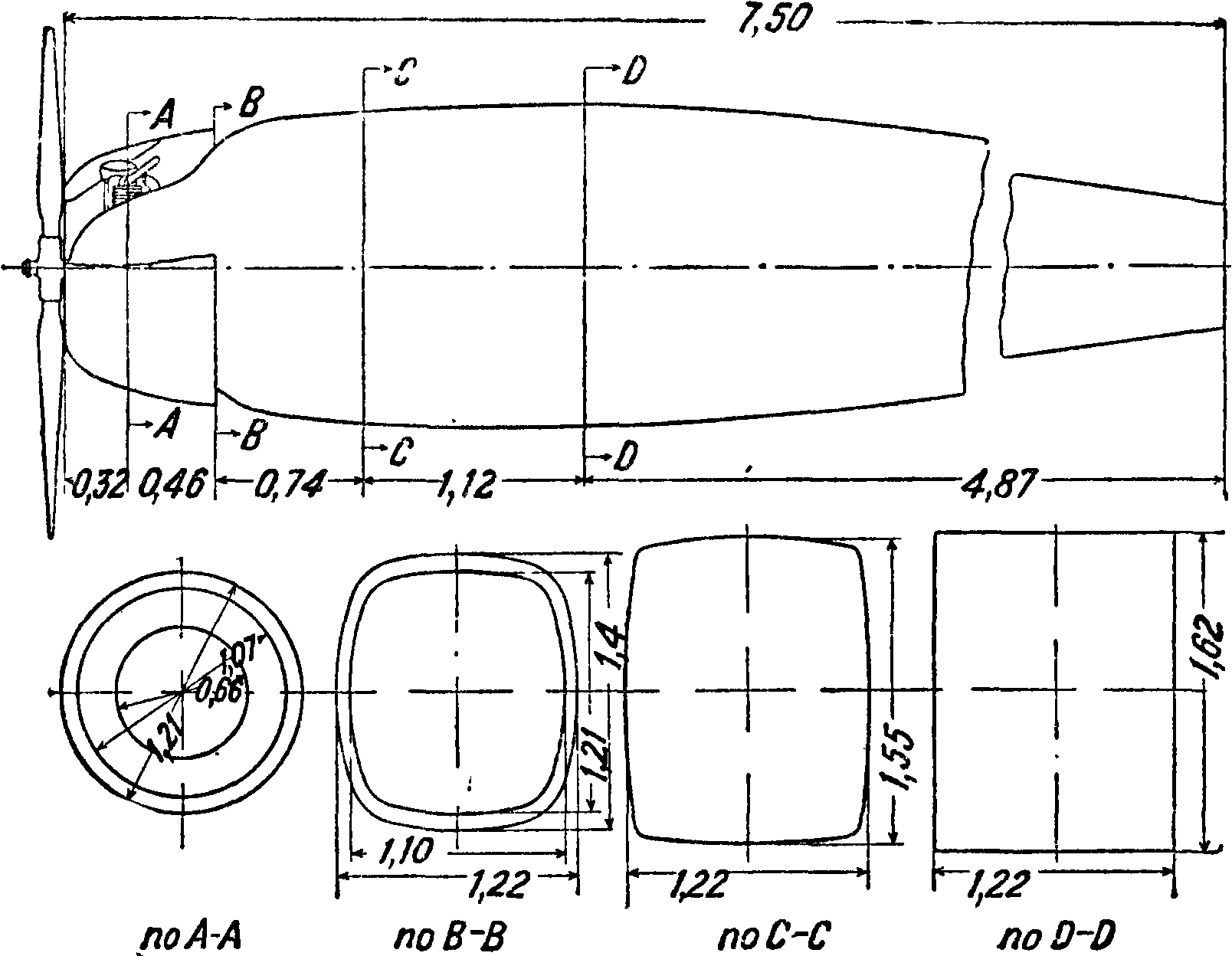
длина тела, a d — диам. и С_ж отнесены к площади ми-

стейшей и наиболее совершенной формой фюзеляжа является форма тела вращения (фигура 71). В табл. 7 приведены результаты испытаний в Варшавской аэродинамич. лаборатории [*] ряда таких тел, характеризующихся различным отношением где I Коэф-ты сил С_уделя, а коэф-ты момента продольной устойчивости отнесены к площади миделя и к длине тела, то есть

Q г“ _ Р „ (-ί _ M_z

QSv2 ’ — qSv2 ^mz ~ _QSvH

Момент определялся относительно оси оз, проходящей через носик тела, причем пикирующий момент считался положительным. Такие тела вращения имеют наименьшее лобовое сопроти-

С„ =

Фигура 71.

вление, причем оно вследствие весьма обтекаемой формы почти целиком определяется силой трения. Из табл. 7 видно, что по мере увеличения отношения коэф. С_х растет; это явление обусловливается возрастанием силы трения за счет увеличения поверхности тела. Наивыгоднейшее отношение длины тела к его диаметру с точки зрения минимума лобового сопротивления равно ~ ^ 3. В зависимости от вида образующей наивыгоднейшее отношение может немного меняться в ту и другую сторону от приведенной средней величины.

Необходимость размещения мотора, кабин летчиков и пассажиров, вооружения и других агрегатов заставляет отступать от наивыгоднейшей формы и придавать поперечному сечению фю.зе-ляжа прямоугольную или овальную форму. Как видно из табл. 7, это тотчас приводит к значительному увеличению коэфициента лобового сопротивления. Дальнейшее усложнение формы приводит к еще большему возрастанию коэф-та лобового сопротивления (фигура 72 — 81). На фигуре 82

^,ίψ

νί ‘ jv?

-SO-

Фигура 72.

приведена схема поплавка гидросамолета, испытанного в Варшавской аэродинамич. лаборатории, а в таблице 7 даны соответствующие аэродинамич. коэф-ты. Коэф-ты сил отнесены к площади миделя, а коэф-ты момента к площади миделя и к длине поплавка. На фигуре 83 дана схема модели фюзеляжа, испытанного в Аахенской аэродинамич. лаборатории (Германия) [²] с целью изучения влияния на величину лобового сопротивления фюзеляжа козырьков и различных ‘форм

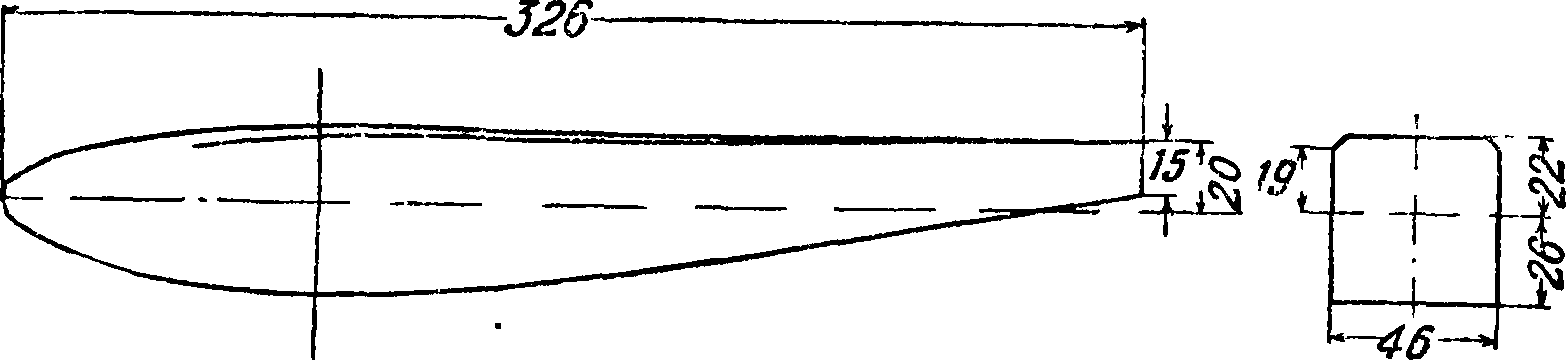
Фигура 74.

397

т->1 I—

—/93-ч

—495-

Фигура 79.

/f

V

Фигура 75.

Фигура 80.

Фигура 76.

Фигура 81.

355-

36 35,5

--94-*	и	*-38^г—б4~*]
	У	i_Ьг^ПТ~~

Фигура 77.

J

-Аэродинамические коэфициенты фюзеляжей и поплавков.

о (М II в	δ О	ОТ О О от ОТ от от © 0,0 и О О ю Ю О Λ Ю CD ОТ —* СО 05 СО «ψ О — 05 CD CD 05 CM О «Ο 00 О OONiON-f o o qo^o о. ОО^О^О^О^ОО^ООДО^ o о о“ о” сГ о сГ о o о о o о" о” о" о“ o o о" 1 II II
	о	О О О Ю и Ю Ю йОййОйОЮОООй О ОТ О СО СО 05 ОТ н“* СЭ н»* — СО NCSHCOiDO OON^CDNNCOlOOvnH^1 OO--OWH Г-н О CM —< —1 T-J.CM. -н СМ_—^г-Н^СМ О О o о” сГ о” о“" о“ о" о" о" о с о о о’ о о о
	Ss О	ООЮОйОЮ ЮОЮОЮООЮЙЮЮЙ Hi* гН Г"1 05 ОТ ,—ι <35 СО ОТ 00 СМ СО ОТ СМ 1—1 от 05 ОТ -сР тг О) О О N ·» ООТ—<-нотСООООТОТСООСО rlvrH.N.n.rl!|l,” ^.О.С^СОО^МСВМгнМ^ нр о" o о” О о” О О*1 3 ОООООООООООО
от и в	δ о	ОООЮЮОО ЙЮОЙОООООЮШО О ОТ СО СМ 00 CM CD t— f-t-OTi—1СОГ->О51>»-нСО05 сантиметров -Η 1—) о -Η <7М О ΟΝ>-ΝΟΟΟηηΜΜρι оооДоо^ OJO 0^05.0^0^0 0 0 0.0 0^ ο ο ο ο ο oo о“ о о о о“ о о о о о" о" о 1 1 1 1 1 1 1 1 1 II 1
	о	Ю и й О in iC Й О О и й и О и й О О |СЙ СО СМ СО СО 00 CD -н t~-CD05OTiHOT05TP00C0CMO -гр СО CD t~- Ή· -Η 05 OniOCROHTlIOifHOOin О О О^ОгнО^ H.0.,H.0.rt.“,.rlH.H.H.0.,l odooddd сГсГооосГосГсГоо σ
	о	О Λ О О и й О ЮйООйОООййОй t>. О 05 05 00 ОТ-М« сантиметров см сантиметров ^ со со от ^ оо сантиметров со со ОО — СО i) СО О -н СО СО о г>-00 СО Г>-ОТ СО О 05 о 1— н О СО СМ СМ. О см^ r-i .О^·—_СМ^--^0_—<.г-^см oO о о o o" o o o о" o <D o o~ o" o“ ©О* сГ
δ II 0	δ* о	ΛΟώ ОТ О »«0Q0OT©0OT©0 со со ю от от сантиметров от Отн“—<с5оот — ~tcovrccoeo СМСМСМтНгНСМг-1 ОСООтН-Ф—COO-HCOiCMCO о О 00^0^0^ о о о о о^О с. ©.о^©^ о" о" o o о~ о" о" о о о o’4 o" о о о о <э о ©*“ II 1 II 1 1 II 1 1 1 1 1 1 1 1
	о	> О О ОТ ОТ О ОТ ОТ ©ОТ ©от©ОТ©ОТО©© OOOOOiOCOt-H-Η ®OOOMiniOOrHr-C5t-N СО СО СО ’Р СО СО ОТ inCONiKJOSNON-iNiOOi 0 0 0^0^0^ О^О^и О^О^^О^-о о^ dodddod © о о о o о ©“ о o" о o4 о
	о1	ОТ ОТ О ОТ О ОТ О ОТОТОООООТОТОТОТОТ ФОООО Ф — ©ОТ©Г^н“СО|СО — 00 н“ ! HP CD С— 00 СО СО -Н го © СО Μ 00 ,-Η. 05 ОТ 05 00 ОТ Ο Ο Ο Ο Ο ή -Η -^0^-^^0_0_-^0_0_ о.©.»-* 0*0 00000 о о о о о о сГо о о о о
Го II 0	«t	ОТ ОТ ОТ О ОТ О ОТ О ОТ ОТ ОТ ОТ ОТ ОТ © ОТ ОТ © СО О О СО СО —< О CMt-OOOOTOTCM-POCMOTt·» S-e5.ci.ri-Н СМ ем О О О О о О О О О ООО О С^о о о о о o ©©"о о©*© ооооооо^оооо 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
	о	О О от от О О ОТ 00000-0 00 от ООот CM СО 05 со Р- ОТ PJOOOClDHClOODN ем г» сантиметров см со со со со со о от г>- от оо от да ео нр е-О О O^OJOO О О.-^О^О^О^О^О^О^ 0*0*0*0*00 o’4 о о“о"о“о“о“о“о о“о“о“о“
	„30 О	О От О От ОТ ОТ ОТ от от ОТ О ОТ ОТ ОТ О от от от от р— гн со —н со со от -^даг-сосОтнао-^-Фот — ь—< СМ СМ С ОТ СО ОТОСОтНМ — СО ч“ СМ СО ОТ СО ооо^оооо оо_ ©©©_©_ 0^0 О^О^О^ о о‘о“ оо’оо“ о о oooodo* ooVoo*
ь и в	«) δ о	ОТ ОТ ОТ ОТ ОТ ОТ ОТ ОТ ОТ О ОТ смемсо-фсо—г-емечемао ниОИНМОООЯСО ООООООО о ® Я,0.0.0.®.®. ®.°.° ° о~ о о" о" о" о’ о" o" o" o о“" 1 1 1 1 1 1 III
	н О	От О ОТ О О ОТ от отототототоооооотО до — .-мм о fH О £- -- — -ФО^наОФдаоесс© СМ СМ СМ СО СО СМ ем СО 05 rt Г- ОТ CD -грооот 0 0^0^0 0^ 0 0_0<ч0 О О^О^О^С 0^0 о о" o’" о" о"о"o’ сГ о о" сГ сГ сГ сГ o o сГ о"" сГ
	О	0 0 0 0 0 0 0 • 0 — 0,0035 — 0,0070 — 0,0265 0 — 0,0210 — 0 0095 0,0025 0,0155 0 0,0030 — 0,0205
Размеры миделя в миллиметров		ОТ ОТ. отОТСоЗн^есГвО 0(МС0тЦй«^00 050Н(М иг- ^ ifj I> t> t> t> N N Ь· t> 00 СО СО § § В 1 x x x 22нн«1Пл hJ* BSSBSSSBSSH со >&>θ<>θ<>θ<>8<>θ<>8<>8<>8<>8<>8<
Форма сечения		круг » » * эллипс квадрат квадрат с закругленными углами прямоугольн. овал фигура 73 фигура 74 фигура 75 фигура 76 фигура 77 фигура 73 фигура 79 фигура 80 фигура 81 фигура 82
Длина в м		ООООООО о Г— От СО нН on от t- 00 ОТ нР ООООООО ООТчрСМ00О50ТОТ05 — СО ч“ lOCO.^* нр Hi* СО СО. to СМСОСОСОССОТСОСО о сГсГ о сГ о сГ о о“" сГ o о“" о о~о о“ сГ о сГ
Эскиз		нН СМ СО чр ОТ CD 05 О — См t - t» t» Гч- t» l·» t» 00 00 0О и 1 1 1 1 1 1 I ΰ ей ΰ и и и tl и tl О ΘΘΘΘΘΘΘΘΘΘΘ

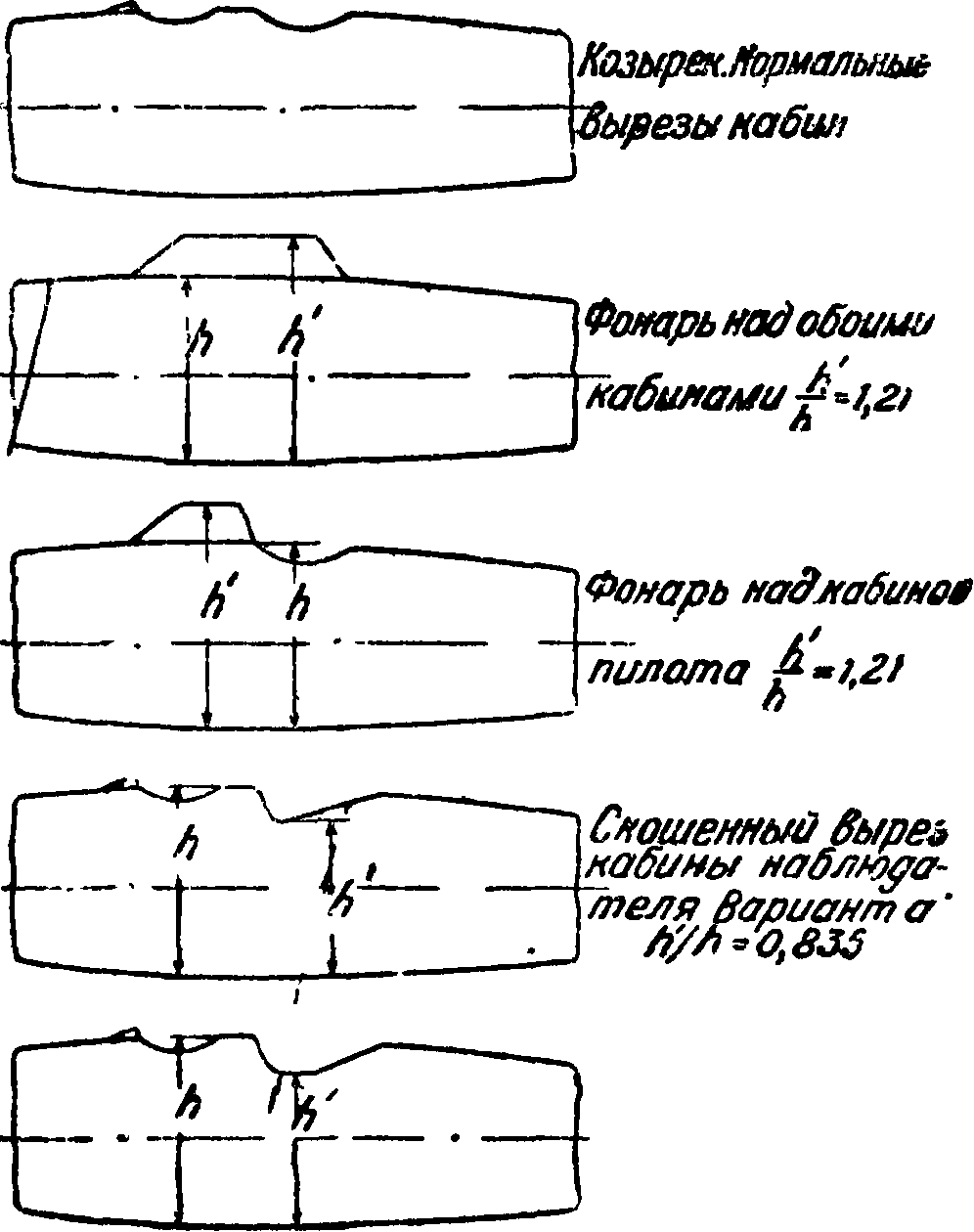
открытых и закрытых кабин (фигура 84). На фигуре 85 приведены результаты испытаний: на вертикальной оси в зависимости от формы кабин на

Тоже Вариант. *

Фигура 84.

Фигура 83.

несены соответствующие числовые значения от-

0_Х

ношения ^, где С,о — коэф. лобового сопротивления гладкого фюзеляжа, а С_х—соответствующий коэф. фюзеляжа с кабиной. Параллельно оси абсцисс отложены отрезки, пропорциональные указанному отношению. Значительное возрастание лобового сопротивления, -вызываемое вырезами и выступами на фюзеляже, заставляет по возможности избегать нарушения плавных контуров фюзеляжей или заключать выступающие детали в обтекатели. Значительное увеличение лобового сопротивления фюзеляжа вызывает мотор с воздушным охлаждением; в этом случае лобовое сопротивле-= ние может возра сти в три раза. ==» Для уменьшения лобового сопроти-=> вления применяют обтекатели различ-^D ной формы, заклю чая отдельно каж-

³ дый цилиндр в ин дивидуальный об-^ текатель или же весь мотор вместе с цилиндром за-^ крывают капотом.

Последнее меро-_ приятие оказывает-

—;гг ся наиболее эффек-

тивным. В Аэро-динамич. лаборатории в Ланглей-фильде (США) проведены весьма подробные изыскания по выбору наивыгоднеяших форм капотов ₉причем выработан хороший тип капота, называе-

Фигура 85.

мый «капотом NACA» (смотрите Самолетостроение). Опыты проводились в аэродинамич. трубе с открытой рабочей частью диам. 6,1 метров с фюзеляжем в натуральную величину и с работающим мотором. Последнее позволило выработать капот, удовлетворяющий не только условию значительного уменьшения лобового сопротивления, но и условиям хорошего охлаждения.

ше переднего диам.) и 3) у - вогнутость кольца, где h—максимальная ордината профиля кольца, отсчитываемая от хорды кольца. Наивыгоднейшая глубина кольца равна 3504-450 миллиметров.

Наивыгоднейшая вогнутость кольца равна ^ 4-^. Наивыгоднейший угол а_усШт близок к 4°, однако

Таблица 8. — Сопротивление фюзеляжа с различными капотами на моторе.

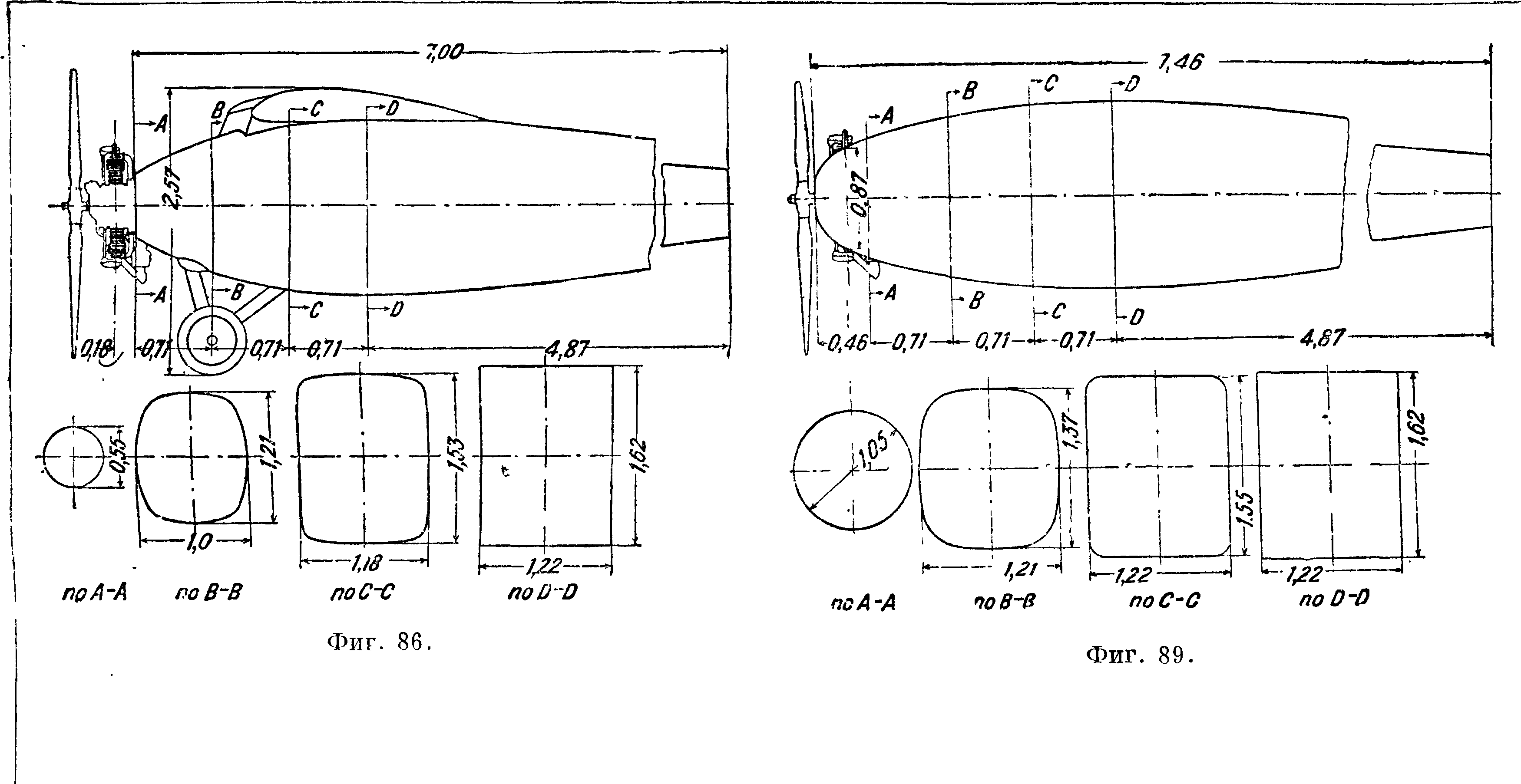
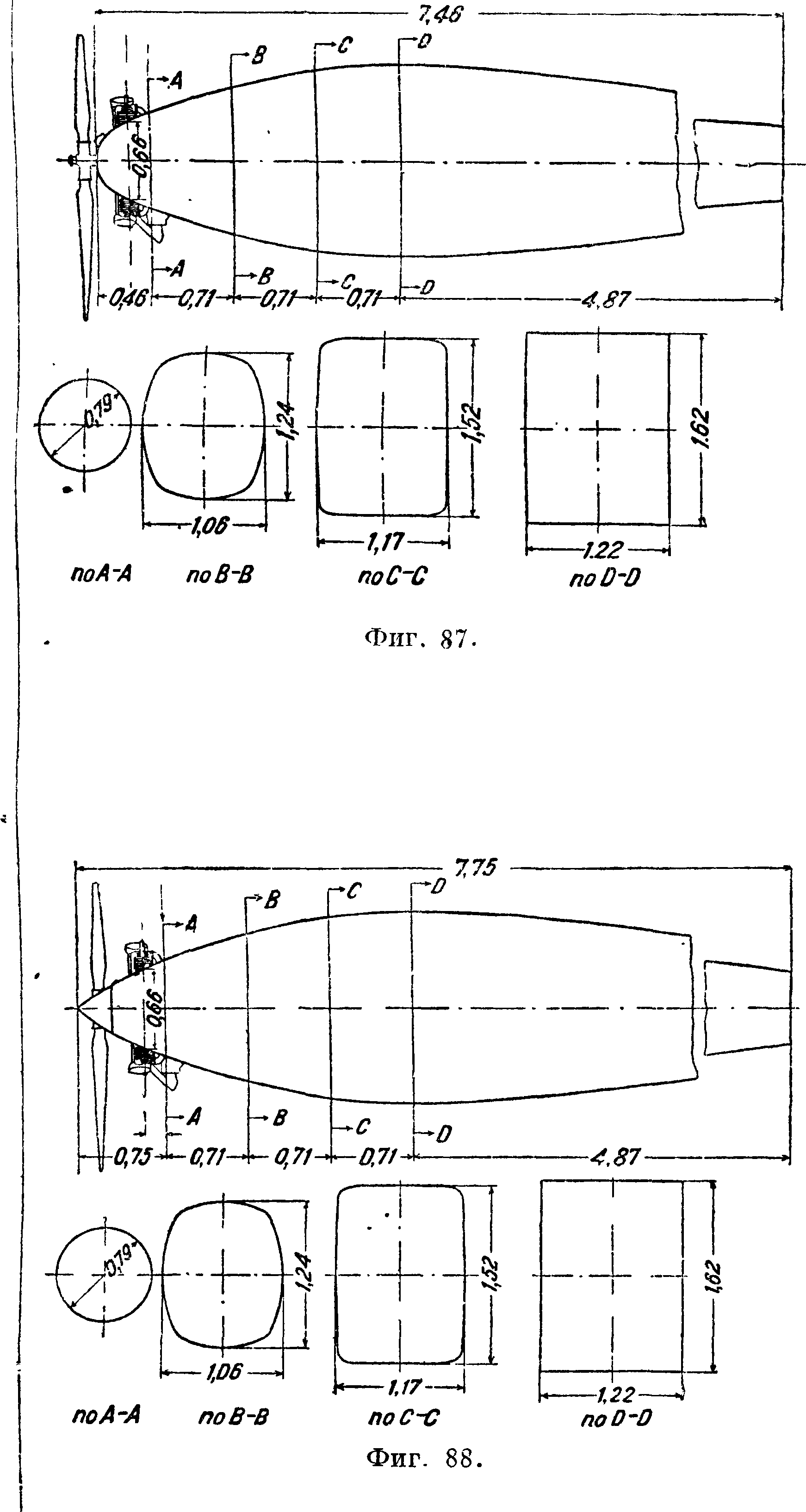
№		Тип капота	Сопротивле	Уменьшение
капотов	Эскиз		ние в килограммах при	сопротивле
			V=1бо км/ч	ния в %
	Фигура 86	Мотор без капота	! 56,5	0,0
5	Фигура 87	Капот № 5 без обтекателя на втулке винта.	I 53,6	5,1
6	Фигура 88	» № 6 с обтекателем на втулке винта.	! 52,3	7,4 21,4
7	Фигура 89	» № 7 без обтекателя на втулке винта.	! 46,4
7	—	То же, но капот изменен для лучшего охлаждения.. ί Капот № 8 с обтекателем на втулке винта.	50,0	11,5
8	Фигура 90		i 45,0	20,4
а	—	То ше, но капот изменен для лучшего охлаждения. Капот № .0 без обтекателя на втулке винта.	47,7	15,6
10	—		28,8	49,0
10	Фигура 91	То же, но капот изменен для лучшего охлаждения.	33,8	40.2 40.2
10	—	То ше, но добавлен обтекатель на втулке винта.	33,8
—		Без мотора, фюзеляж спереди закруглен..	18,0	68,1

На фигуре 86 — 91 приведены чертежи фюзеляжа с капотами различной формы, а в таблице 8 приведены результаты испытаний [³]. Наилучшим капотом оказался капот № 10 (фигура 91); в этом случае уменьшение лобового сопротивления фюзеляжа достигает 40% при хорошем охлаждении. Применение капотов NACA позволяет увеличить максимальную скорость самолета на 5—10%. С физич. точки зрения наличие капота NACA вызывает уменьшение скорости потока в области расположения цилиндров и улучшение обтекания фюзеляжа за цилиндрами (уменьшение и значительное сужение вихревой зоны). Еще больший эффект по сравнению с эффектом уменьшения лобового сопротивления фюзеляжа вызывает капот NACA при установке его на мотор, находящийся в гондоле. На фигуре 92 приведен изолированный мотор Райт «Уирлуинд» в 200 л.с., впоследствии смонтированный в шестиметровой аэродинамич. трубе в Ланглейфильде для определения лобового сопротивления [⁴]. На фигуре 93 приведен этот мотор в моторной гондоле, а на фигуре 94—мотор в гондоле с капотом NACA. В табл. 9 даны результаты испытаний. Рассмотрение таблицы показывает, что вызванное капотом уменьшение лобового сопротивления достигает 72% от сопротивления гондолы с открытым мотором.

Другой разновидностью обтекателей моторов с воздушным охлаждением являются кольца Тоуненда [V] (Ф^иг· 95). На фигуре 96 дан профиль кольца. Уменьшение лобового сопротивления, вызываемое кольцом Тоуненда, объясняется тем, что вследствие скоса потока за кольцом вихревая зона, возникшая за цилиндрами, суживается и обтекание в кормовой части фюзеляжа улучшается. В табл. 10 приведены основные характеристики колец, испытанных в ЦАГИ: 1) i — глубина кольца, 2) а_уст — угол, составляемый хордой профиля кольца м осью мотора (угол o._ycWt считается положительным в том случае, если’ задний диаметр кольца боль его точное значение зависит как от глубины кольца, так и от формы носовой части фюзеляжа. Наибольшее влияние на лобовое сопротивление

Таблица 9 .—С сопротивление мотора и моторной гондолы при скорости г?=160 км] час.

Эскиз	Тип мотора	Лобовое сопротивление в килограммах	Уменьше ние сопротивления в %
Фигура 92	Изолированный мотор воздушного охлаждения	80,5	0
Фигура 93	Мотор с моторной гондолой без капота	70,0	13
Фигура 94	Мотор с моторной гондолой и капотом NACA	19,4	76

оказывает угол а_ус7Пя9 неправильный выбор его может привести к весьма малому уменьшению лобового сопротивления. Необходимо, чтобы угол характеристики колец Тоуненда и с о о т-ния коэфициента лобового сопр отивле-

атаки кольца по отношению к местному направлению скорости был близок к критич. углу атаки, соответствующему С_{у тах}, но не превышал бы его. В табл. 10 кроме основных характеристик колец приведены результаты испытаний фюзеляжа с различными кольцами в большой аэродинамич. трубе ЭАО ЦАГИ. Кольца .Тоуненда по сравнению с капотами NAGA менее эффективны, однако они весьма удобны в э^с-плоатации, не затрудняют доступа к мотору и

Таблица 10.—О сновные ветствующие значе ния фюзеляжа (по опытам ЦАГИ).

Основные характери стики		Номер в		а р и а н т а			С индивидуальными обтекателями	Без кольца и без обтекателей
	2	3	4	5	6	la*
h	1	1	1	1	1	1
ί	ю	6	8	8	~s	8
	8	8	4	10	8	6	_	—
уст· t В миллиметров.	853	353	353	353	450	353	—	—
Οχ.	0,303	0,295	0,280	0,305	0,303	0,308	0,360	0,380
Уменьшение
Οχ в %.	20,3	22,4	26,4	19,7	20,3	19,0	5,3	0

* Кольцо 1а имело меньший диаметр и колпаки-обтекатели, над клапанными головками цилиндров.

;__:___

позволяют монтировать их без переделки фюзеляжа на уже готовом самолете.

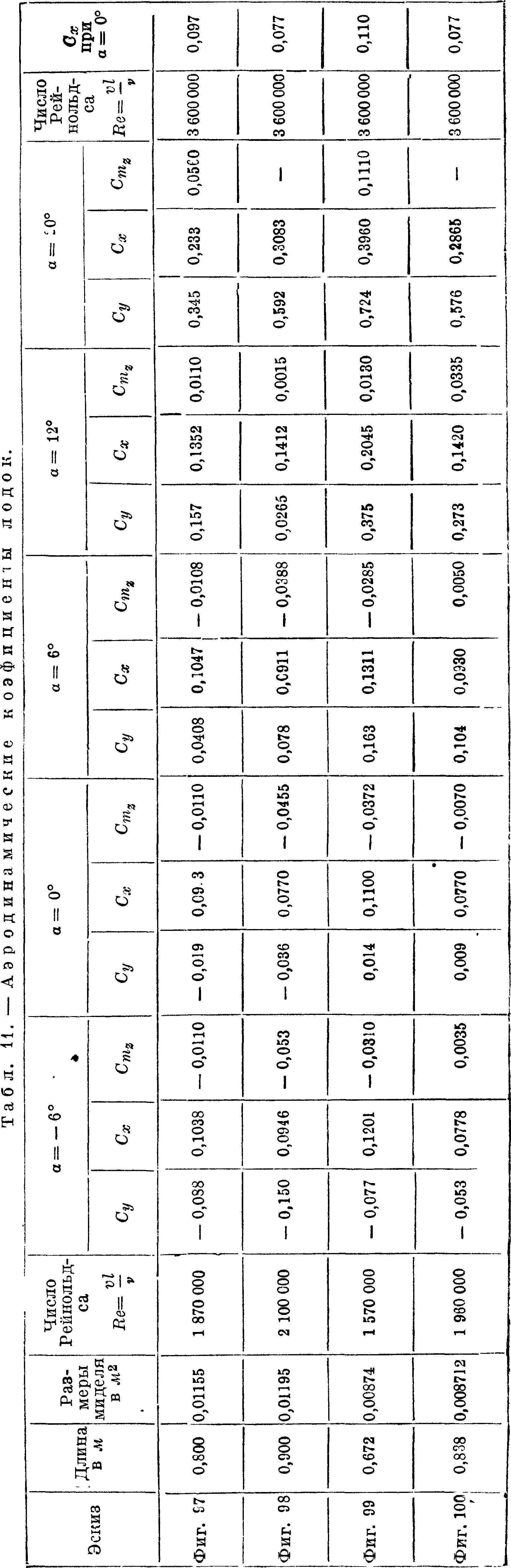
На фигуре 97—100 представлены общие виды моделей лодок, испытанных в трубе Т-III ЭАО ЦАГИ [⁸], а в таблице 11 приведены значения аэродинамич. коэф-тов С_х и С_у9 отнесенных к площади миделя, и значения коэф-та С_т момента продольной устойчивости относительно носиков лодок (оси А), отнесенного к площади миделя и к длине лодок. Пикирующий момент считается положительным.

Ь) Лобовое сопротивление колес, шасси и лыж. На фигуре 101 приведены схемы колес, испытанных в натуральную величину в трубе Т-I ЭАО ЦАГИ [⁹]. Основные геометрия. характеристики приведены в таблице 12. Спицы колес № 1 и № 2 были обтянуты полотном. Результаты испытаний на С_х по v м/ск приведены на фигуре 102. Коэф. С_х относился к площади, равной произведению D-d (фигура 101). Из рассмотрения фигура 102 видно, что форма колеса оказы

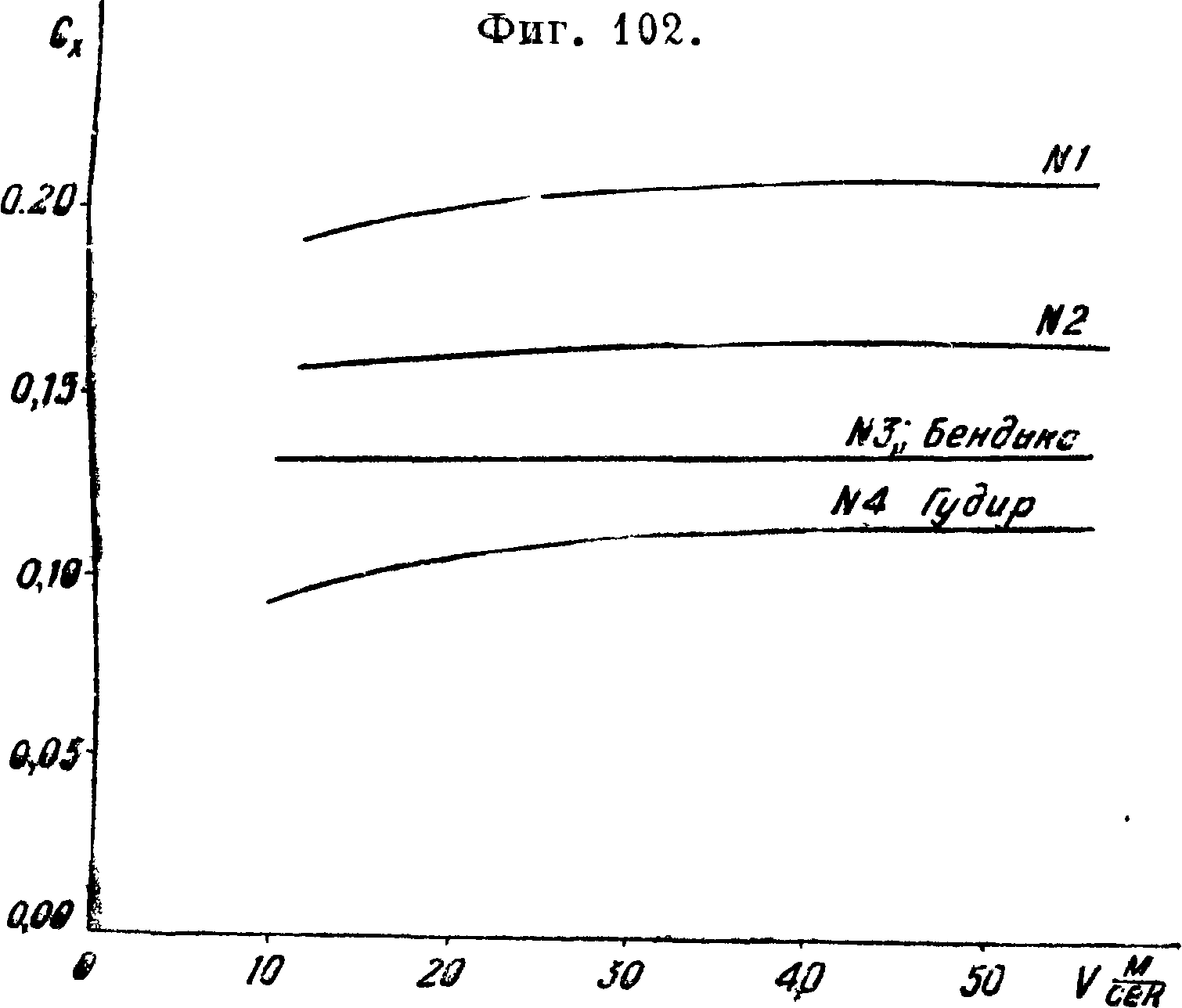
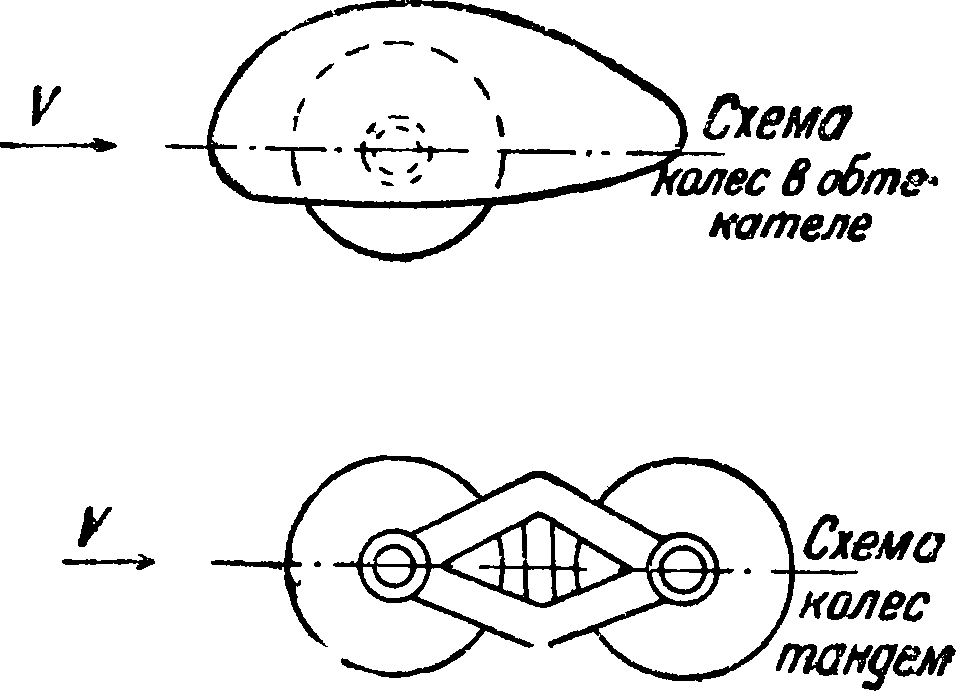
вает большое влияние на величину коэф-та лобового сопротивления; величина его для испытанных колес колеблется при v —50 м/ск в пределах 0,115-1-0,212. Лобовое сопротивление колес при v=max составляет в среднем 8—10% от полного лобового сопротивления самолета. Для уменьшения лобового сопротивления колес их располагают тандем или заключают в обтекатели. На фигуре 103 даны схемы таких расположений,

а в таблице 12 указаны соответствующие значения коэф-та ·С_х там же указан % снижения коэф-та С_х в случае заключения колес в обтекатели. Кроме того в таблице 12 приведены результаты испытаний спаренных колес (фигура 103), устанавливаемых иногда на тяжелых самолетах. На фигуре 104 указана зависимость коэф-та С_х колеса от для колес с открытыми спицами и для колес с затянутыми спицами [¹⁰] (смотрите Колесное производство, авиационные колеса).

Фигура ЮЗ.

Схема спарен“ ных нанес

Лобовое сопротивление шасси обычно принимается равным сумме сопротивлений изолированных колес, стоек и подкосов, однако такое определение вследствие взаимного влияния отдельных элементов шасси может оказаться не совсем верным, и для более точного ответа лучше производить испытания в аэро-динамич. трубе целого шасси. Лобовое сопротивление шасси при v=max составляет в среднем 16—

20% от полного лобового сопротивления самолета, но оно м. б. значительно уменьшено применением обтекателей. Капотирование шасси с одиночными колесами вызывает уменьшение лобового сопротивления в среднем на 30%.

Капотирование шасси тяжелых самолетов (колеса на тележке) вызывает уменьшение лобового сопротивления на 50— 75%—в зависимости от формы шасси, формы тележки и обтекателей [®].

На фигуре 105 дан общий вид авиационной лыжи (смотрите Лыжи), на фигуре 106 приведены результаты ее испытаний в натуральную величину на ^СХ, Су К в трубе Т-I ЭАО ЦАГИ при скорости потока v==37,3 метров ск. Коэф-ты сил относились к площади опорной поверхности лыжи, а коэф. момента был отнесен к площади опорной поверхности лыжи и к ее длине. Момент определялся относительно оси крепления лыжи: пикирующий момент считался положительным. Б среднем минимальный коэфи-циент С_х для лыж без обтекателей на кабанчике м. б. принят равным 0,014, а в случае обтекателя на кабанчике G_xmin в среднем равен противления стоек и обтекателей труб относят к площади миделя. Коэф. С_х лобового сопротивления стоек и обтекателей зависит от числа Рейнольдса, эта зависимость особенно велика

Таблица 12 .—К оэфициенты лобового сопротивления ави а“ц ионных колес.

1 Тип колеса	D	d	S=D - d	Сх		% сниже
(фигура 101 и 103)	в м	в м	в м	без обтекателя	с обтекателем	ния Сх
Колесо № 1 одиночное. Колеса № 1 спаренные (щель между колесами	0,70	0,12	0,084	0,212	0,090	57,5
60 миллиметров)..	0,70	0,12	0,084	0,500	0,208	58,4
Колеса № 1 тандем.	0,70	0,12	0,084	0,470	0.195	58,5
Колесо № 2 одиночное. Колеса № 2 спаренные ицель между колесами	0,75	0,125	0,09375	0,168	0,088	47,6
25 миллиметров).. Колесо № 3 «Бендикс»	0,75	0,125	0,09375	0,390	—	—
тормозное одиночное. Колесо балонное № 4	0,90	0,20	0,180	0,135	—	—
«Гудир» одиночное. Колеса балонные № 4	0,635	0,28	0,1788	0,115	0,075	34,8
«Гудир» тандем.	0,635	0,28	0,1788	0,237	0,133	43,9

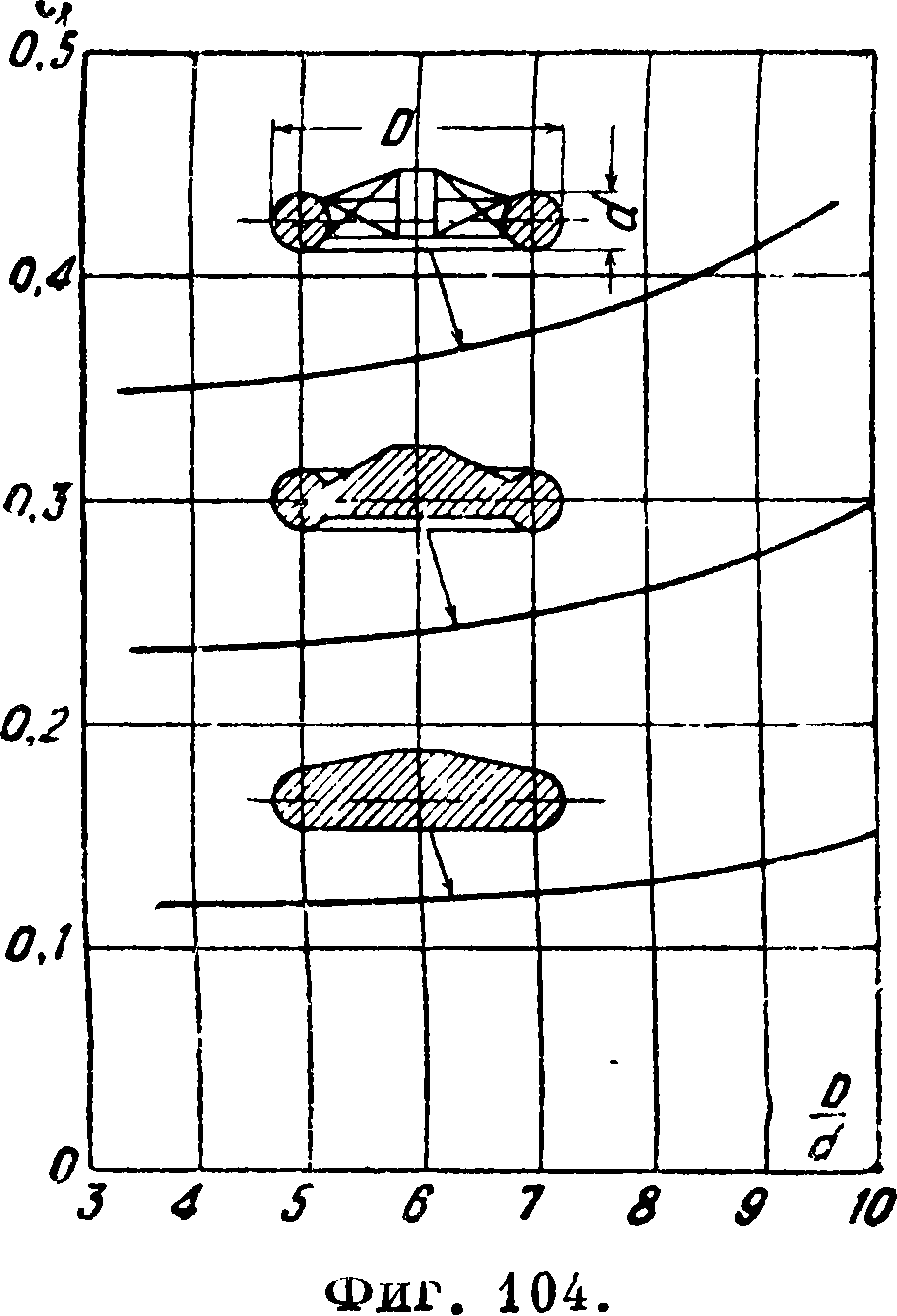
при малых числах Рейнольдса. При увеличении числа Рейнольдса коэф. С_х быстро уменьшается, стремясь асимптотически к некоторому пределу (подробнее о зависимости коэфициента С_х стоек от числа Рейнольдса и турбулентности см. главу «Лобовые сопротивления простейших тел»).

При числах Рейнольдса Re=~ > 130 000, где а—ширина стойки или обтекателя, коэфициецт С_х можно приближенно принять постоянным и

Таблица 13.—К о о р д и н а т ы профилей стоек.

Абсцисса в % от хорды	Ординаты в % от хорды
	№ 1	№ 2	№ 3
0	0,00	0,00	0,00
ь	6,60	7,55	8,80
10	9,00	10,28	12,00
20	11,48	13,10	15,30
30	12,35	14,10	16,45
40	12,50	14,28	16,65
50	12,00	13,70	16,00
60	10,78	12,28	15,00
70	9,23	10,53	12,30
80	7,10	8,10	9,45
90	4,25	4,87	5,65
95	2,44	2,79	3,25
100	0,00	0,00	0,00

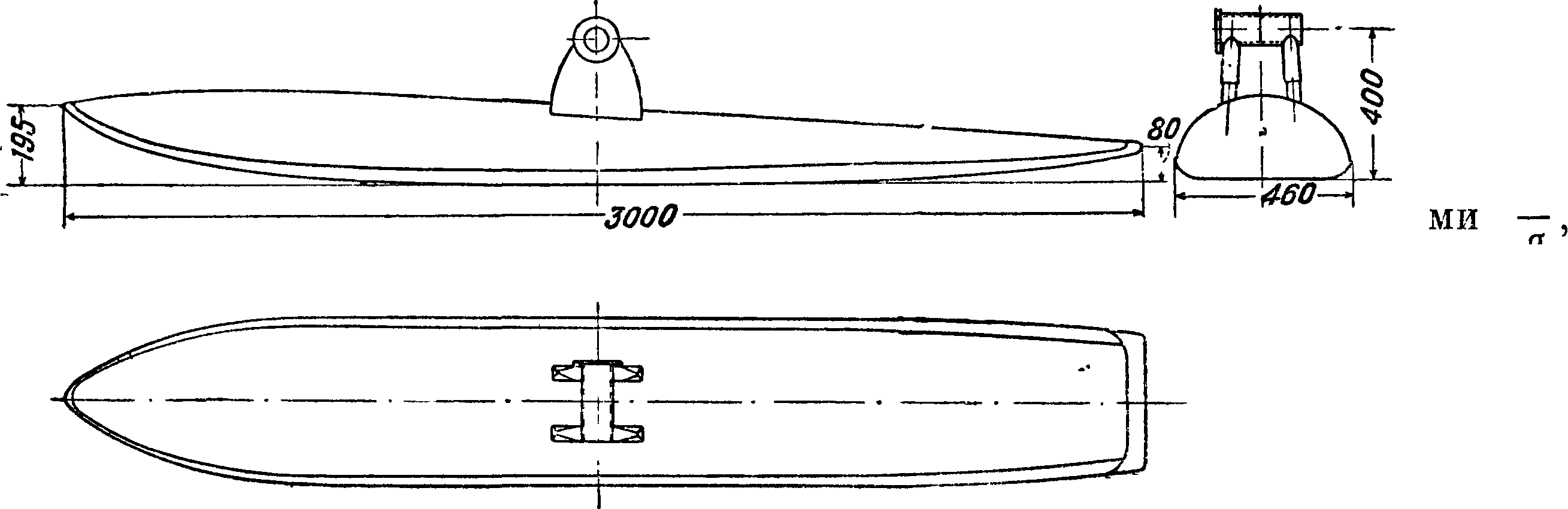
Фигура 105.

0,008, то есть обтекатель вызывает снижение сопротивления в среднем на 43%.

с) Лобовое сопротивление стоек, обтекателей труб, проволок, тросов, тендеров и лент. Коэф-ты со не зависящим от числа Рейнольдса. На фигуре 107 приведены три профиля хорошо обтекаемых стоек, характеризующихся различными отношения-

где b — глубина стойки. На этой же фигуре указаны соответствующие коэф-ты лобового сопротивления [¹⁰]. В табл. 13 даны координаты стоек в % от хорды. На фигуре 108 приведены схемы различных обтекателей труб и указаны соответствующие коэф-ты С_ХлДля учета лобового сопротивления концевых креплений стоек и обтекателей за расчетную длину их принимают 1_расч.= 1+0,6 метров При наклонно расположенных стойках и обтекателях за расчетную длину принимают 1_ра€Ч.=^.+ ^м>

где l_np,—длина проекции стойки или обтекателя на плоскость, перпендикулярную к потоку.

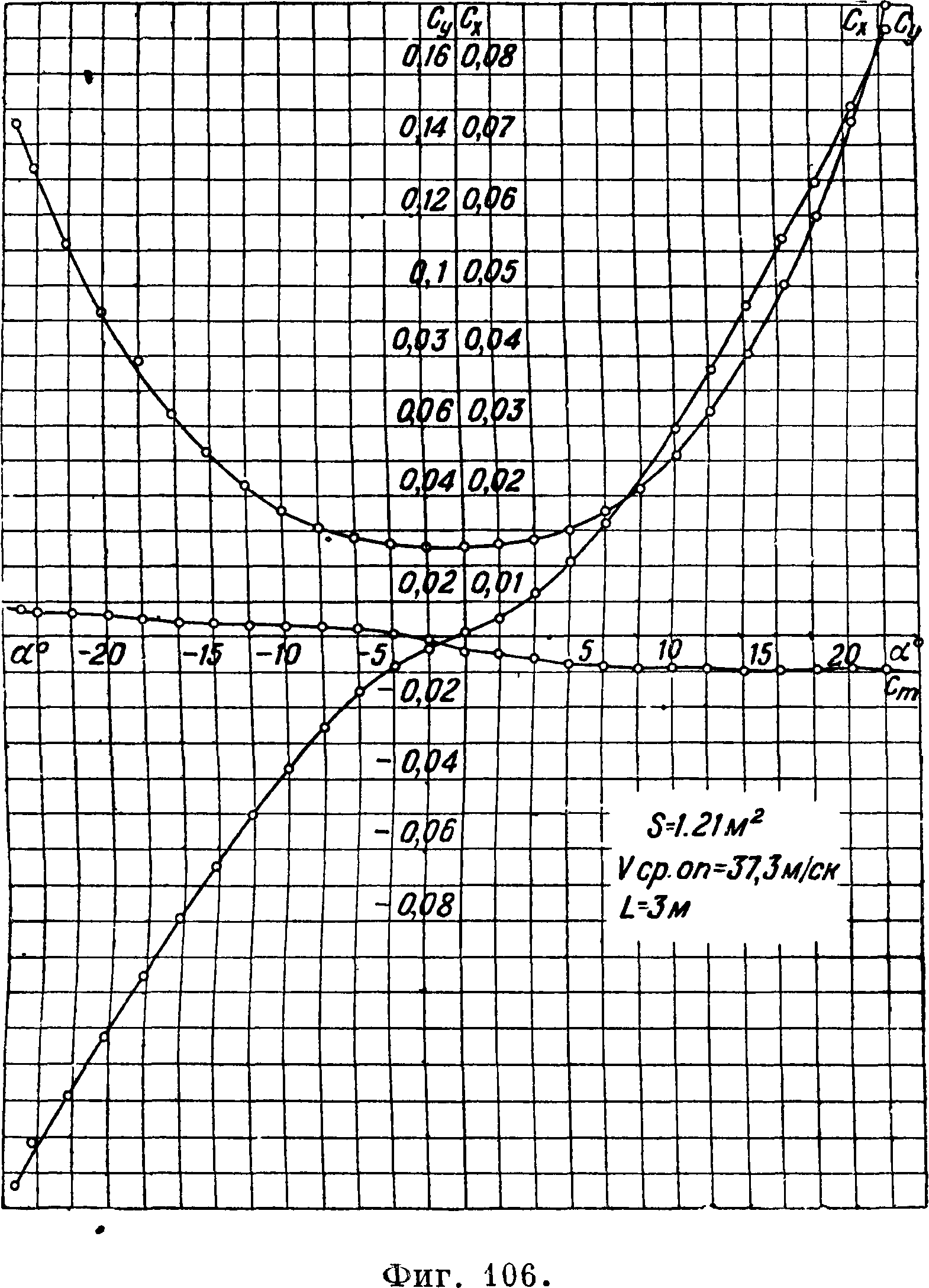
Коэф-ты сопротивления тросов и проволок относят к площади миделя, то есть к произведению длины на диаметр. В табл. 14 приведены осно-

Таблица 14.—Основные данные тросов двойного плетения, испытанных в ЦАГИ.

Диам. троса d в миллиметров	Число стренг *1	Диам. стренг в миллиметров	Число проволок в стренге	Диам. проволоки в миллиметров	Отношение 1 *2 λ-т
8,10	7	2,6	7	0,8	371
7,09	7	2,2	19	0,4	424
6,39	7	2,0	19	0,3	470
5,03	7	1,6	7	0,5	598
4,00	7	1,2	7	0,3	750
3,01	7	0,9	7	0,2	998
2,01	7	0,5	7	0,1	1437
12,06	7	4,0	10	0,9	249
14,96	7	5,0	30	0,6	201
*1 У тросов в центре находится одна стренга, а все
остальные расположены вокруг центральной в один ряд. *2 1 — длина троса.

вные данные тросов, испытанных в трубе Т-I ЭАО ЦАГИ [^п], а на фигуре 109 результаты этих испытаний. По оси ординат отложены коэф-ты лобового сопротивления С_х, а по оси абсцисс числа Рейнольдса. Для сравнения на этой же диаграмме нанесены результаты испытания круглого цилиндра (проволоки). Для учета лобового сопротивления концевых креплений проволок и тросов за расчетную длину принимают 1_расч.⁼ +0,6 метров При наклонно расположенных проволоках за расчетную длину принимают: при

90°>а°>60° 1_р^,сч. ⁼ Jsina + 0,6 м, при 60°>

>а°>30° 1_расч.== sin 0,8а + 0,6 метров При наклонно расположенных тросах за расчетную длину принимают 1_расч.=1_пр.+ 0,6 м, где 1_ПР—длина проекции троса на плоскость, перпендикулярную к потоку. Лобойое сопротивление тендеров по опытам ЭАО ЦАГИ [^п] м. б. принято равным 1,7 Q_m, где Q_m—лобовое сопротивление троса длиной, равной длине тендера с двумя заплетками, и диаметром, равным диам. ушка тендера. Коэф. сопротивления лент относится к площади миделя. В табл. 15 приведены основные характеристики авиационных лент, испытанных в трубе Т-1 ЭАО ЦАГИ [“]; значение указанных в таблице 15

Таблица 15.— Основные данные авиационных лент, испытанных в ЦАГИ.

№ ленты	W в миллиметров	Т в миллиметров	п в миллиметров	г в миллиметров	W т	-4
6	8,30	2,00	12,00	0,44	4,15	1500
10	13,00	3,50	20,58	0,76	3,72	856
12	17,25	4,25	24,90	0,92	4,06-	7U5
16	21,50	5,32	34,32	1,27	4,04	562

характеристик понятно из фигура 110, на которой дано поперечное сечение ленты. На фигуре 111 приведена зависимость коэф-та лобового сопротивления испытанных лент от числа Рейнольдса

Re=^v-^₎ где Т—толщина ленты. Для учета лобового сопротивления концевых креплений лент за расчетную длину принимают 1_расЦт=1- -+0,8 метров При наклонно расположенных лентах за расчетную длину принимают 1_расч,= l_np.-l· +0,8 м, где l_npm—длина проекции лент на плоскость, перпендикулярную к потоку.

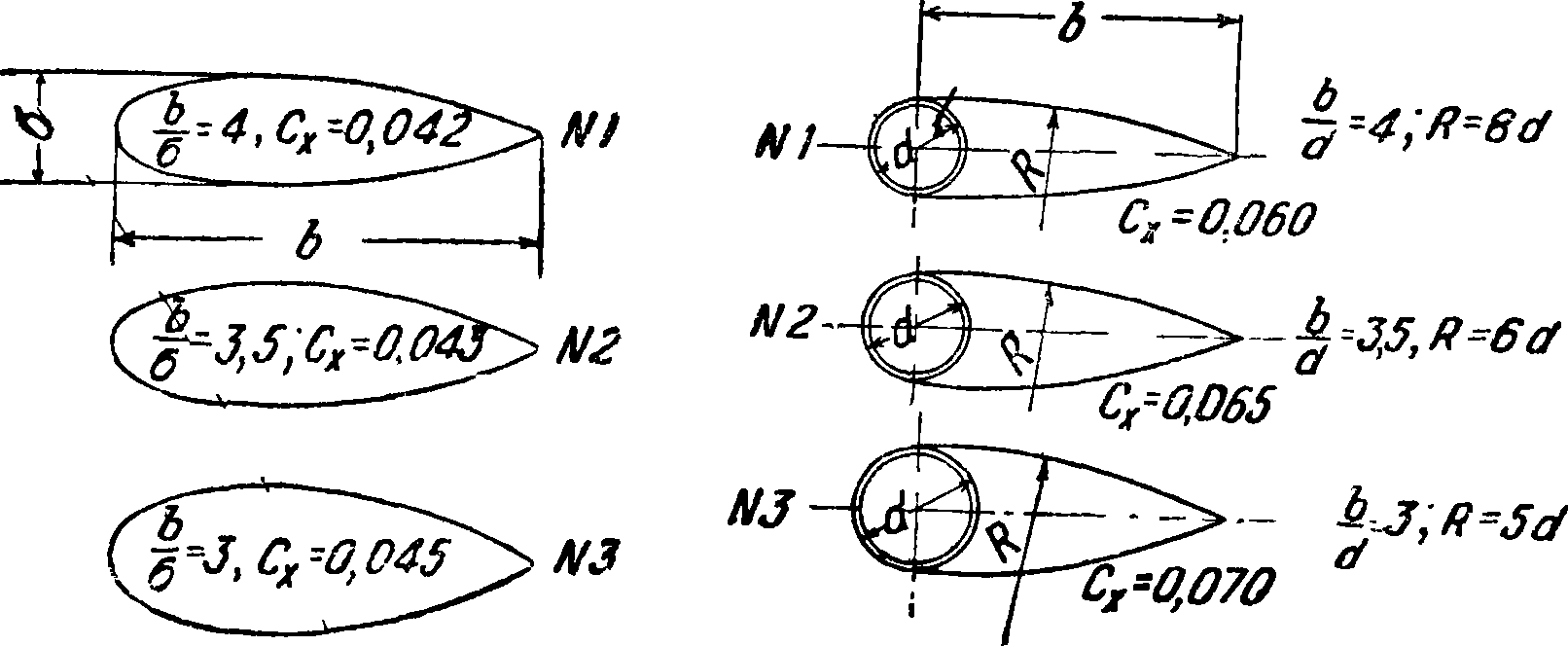
Фигура 107. Фигура 108.

d) Аэродинамические характеристики горизонтальных оперений. На фигуре 112 дана схема горизонтального оперения, испытанного в трубе НК-I МАИ при v=32 м/ск, а на фигуре 113 приведена зависимость коэф-та нормальной силы от угла атаки оперения при различных углах отклонения рулей высоты [¹²]. Эффективность рулей зависит от отношения площади рулей и площади оперения, от формы профиля, от формы оперения и от типа компенсации и размеров компенсаторов [¹²,¹³,^г4]. Подбор и расчет оперения следует делать с учетом интерференции фюзеляжа и оперения, с учетом скоса потока от крыла и с учетом влияния струи винта |¹⁵, ¹⁶, ¹⁷, ¹⁸, ¹⁹, ²⁰].

e) Сопротивление турельных пулеметов. На фигуре 114 и 115 даны схемы различных расположений спаренных пулеметов Льюиса и пулемета Максима с указанием соответствующих коэфициентов R_x=, где Q — лобовое сопротивление пулемета при нормальных условиях (то есть при р=760 миллиметров и ί=15°). При подсчете лобового сопротивления пулеметов в условиях, отличных от нормальных, следует пользоваться ф-лой

Q=A.R_x.v

где Δ=-. Значения Δ в зависимости от высоты

«?0 пт над уровнем океана приведены в главе «Международная стандартная атмосфера» (табл. 19).

2. Интерференция частей самолета. Под интерференцией частей самолета подразумевают их взаимное влияние друг на друга, вернее говоря, их взаимное влияние на поток, обтекающий рассматриваемую комбинацию, состоящую из отдельных элементов. Взаимное влияние частей самолета друг на друга может привести или к увеличению лобового сопротивления или к его уменьшению, то есть в первом случае лобовое сопротивление всей установки будет больше суммы лобовых сопротивлений изолированных деталей, во втором случае оно будет меньше этой суммы.

В первом случае интерференционное сопротивление будет положительным, во втором — отрицательным. В худших случаях положительное интерференционное сопротивление мо>кет свести нанет летные свойства самолета, особенно такие, как потолок, скороподъемность, дальность, маневренность и посадочная скорость.

Интерференция частей самолета может привести не только к увеличению лобового сопротивления, но и к уменьшению, и иногда значительному, подъемной силы. По своей сущности явление интерференции заключается в том, что в некоторых случаях при сочетании частей самолета изменяются скорости и давления в местах сочленений, в других случаях сочетание частей вызывает нарушение обтекания и служит причиной возникновения или ускорения срыва потока. Первый фактор может выз-

интерференцию. Явление интерференции становится все более и более заметным по мере совершен ствования аэродинамич форм отдельных элементов

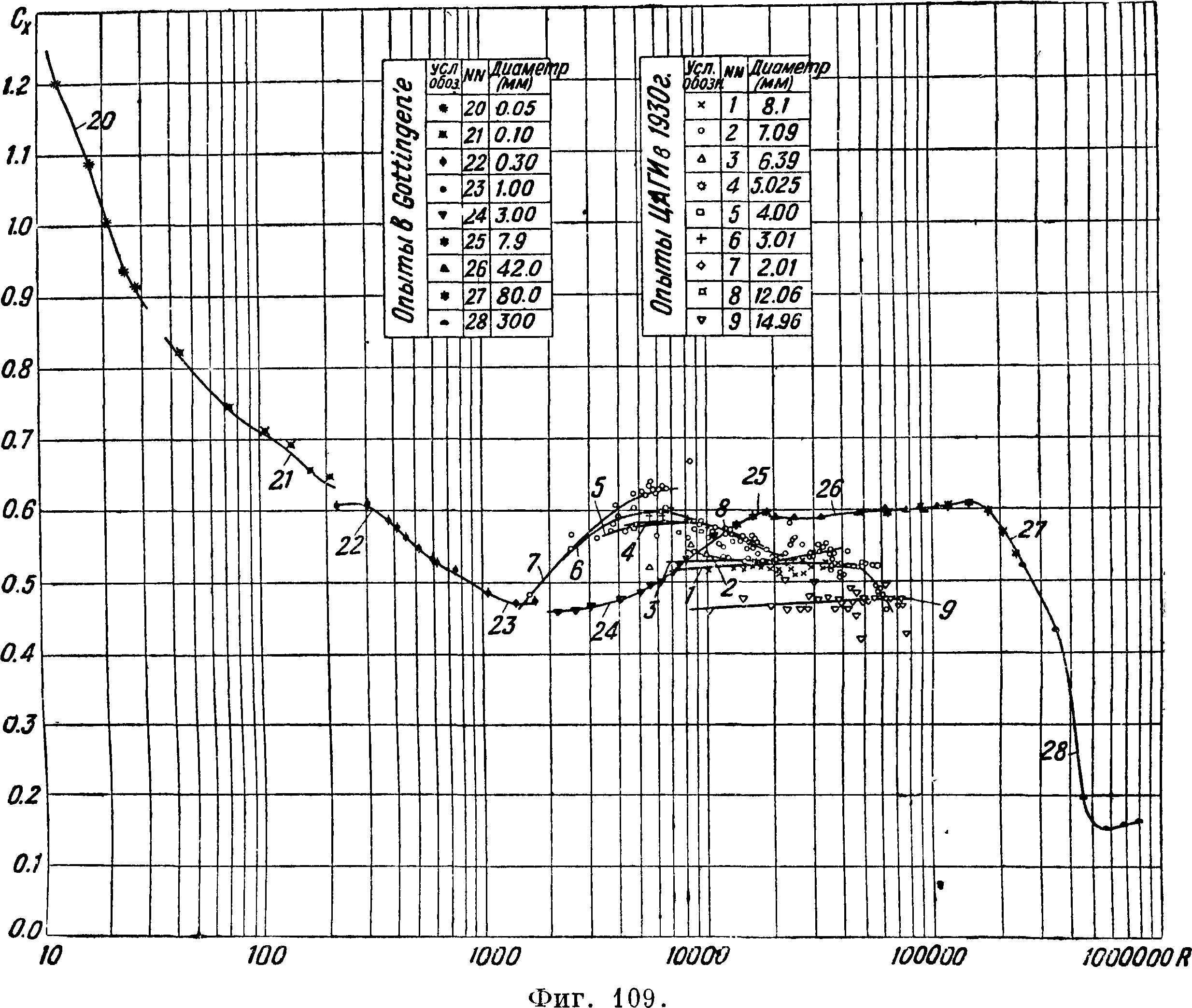
Фигура но.

					>
			—Лента N6 Пента.N10 Лента N12 —Лента N16 -+~*-Лента N16 [повторный опыт)
мв
	Λ	N10
		ч“.				N12
									-Г"

5000

1QOOO

Фигура 111.

15000

20000R

вать положительную или отрицательную интерференцию, второй вызывает всегда“положительную а) Интерференция круглых цилиндров, стоек и лент. При расположении двух круглых цилиндров один за другим (тандем, возникает отрицательная интерференция. В этом случае лобовое сопротивление двух цилиндров меньше суммы сопротивлений изолированных цилиндров, кроме того лобовор сопротивление каждого цилиндра в присутствии другого меньше сопротивления изолированного цилиндра. На фигуре 116 приведены результаты ис“ пытания круглого цилиндра диам. <2=11,5 миллиметров и длиной 2=600 миллиметров Профиль оперений в присутствии дру-

—— того цилиндр та-

Фигура 112.

$рул. выс. ~⁰’3333₀η?μ

кого же диаметра, но длиной 2=1 500 миллиметров. Опыты проводились в трубе НК-I МАИ при числе Рейнольдса Re — ~=25 000 [²¹]. На фигуре

116 по оси ординат отложен коэф. лобового сопротивления C_Xi а по оси абсцисс — расстояние между центрами цилиндров в диаметрах цилиндра, то есть Δ= где а—расстояние между центрами цилиндров. Пунктиром показана величина коэф-та лобового сопротивления изолированного цилиндра. Через С_х обозначен коэф. сопротивления переднего цилиндра в присутствии заднего, а через С"_х коэф. заднего цилиндра в присутствии переднего. Среднее значение, равное ^С* ⁵ обозначено через С_х0. Уменьшение сопротивления переднего цилиндра в присутствии заднего объясняется подпором воздуха, вызванного задним цилиндром. Уменьшение сопротивления заднего цилиндра обусловливается тем, что задний цилиндр находится в аэродинамич.

0п

1

I

0,5

*21

Г J

wL

у

у

О

0,4

у

я

У

у

у.

ί

Ί

03

У

У

У

У

у

Г

у

у

у

У

у

№

У

у

У

У

у С

р 25

У

А

А

У

У

А

У

к

А

7

А

у у

у

А

у

ту

У

/,

У

У

Δ

У

A

У

У

у

У

у.

у

у

у

у

Ά

У

У

го

Л

У

У,

У

/у

у

Р

У,

7

0

2

0

ОС‘

/t

У

у

V

ь,

у

у

У

у

у

У

У

<

у

У

У,

У

А>

У

У

у

у.:

У/.

у

у

у

у

У

А

оА

/у-

у

А

у

у

У

У

%4

5?оп пп-0,0665м2

Δ

£

у

^оил.вьи

* 0

0222мг=33,3%

опи

✓

А.

0,5

•

,6

Фигура из. тени, вызванной передним цилиндром. Отрицательное сопротивление заднего цилиндра при близких расстояниях цилиндров друг от друга вызывается подсасывающим эффектом разрежения, господствующего позади переднего цилиндра. Рассмотрение диаграмм кроме того показывает,

что по сравнению с задним цилиндром влияние переднего цилиндра интенсивнее и распространяется на значительно большее расстояние. Для учета лобового сопротивления концевых креплений на каждую пару круглых проволок следует прибавлять по 1 метров Учет наклона смотрите выше. На фигуре 117 приведена схема расположения цилиндров-тандем при угле сноса а°, a на фигуре 118 даны результаты испытаний. По оси ординат отложен коэф. лобового сопротивления центрального цилиндра, а по оси абсцисс — угол сноса а° [²¹]. Опыты проводились при трех расстояниях между осями цилиндров. При углах сноса, близких к 90°, лобовое сопротивление центрального цилиндра больше сопротивления

изолированного цилиндра (С_х изображен пунктиром), причем сопротивление тем больше, чем ближе друг к другу расположены цилиндры.

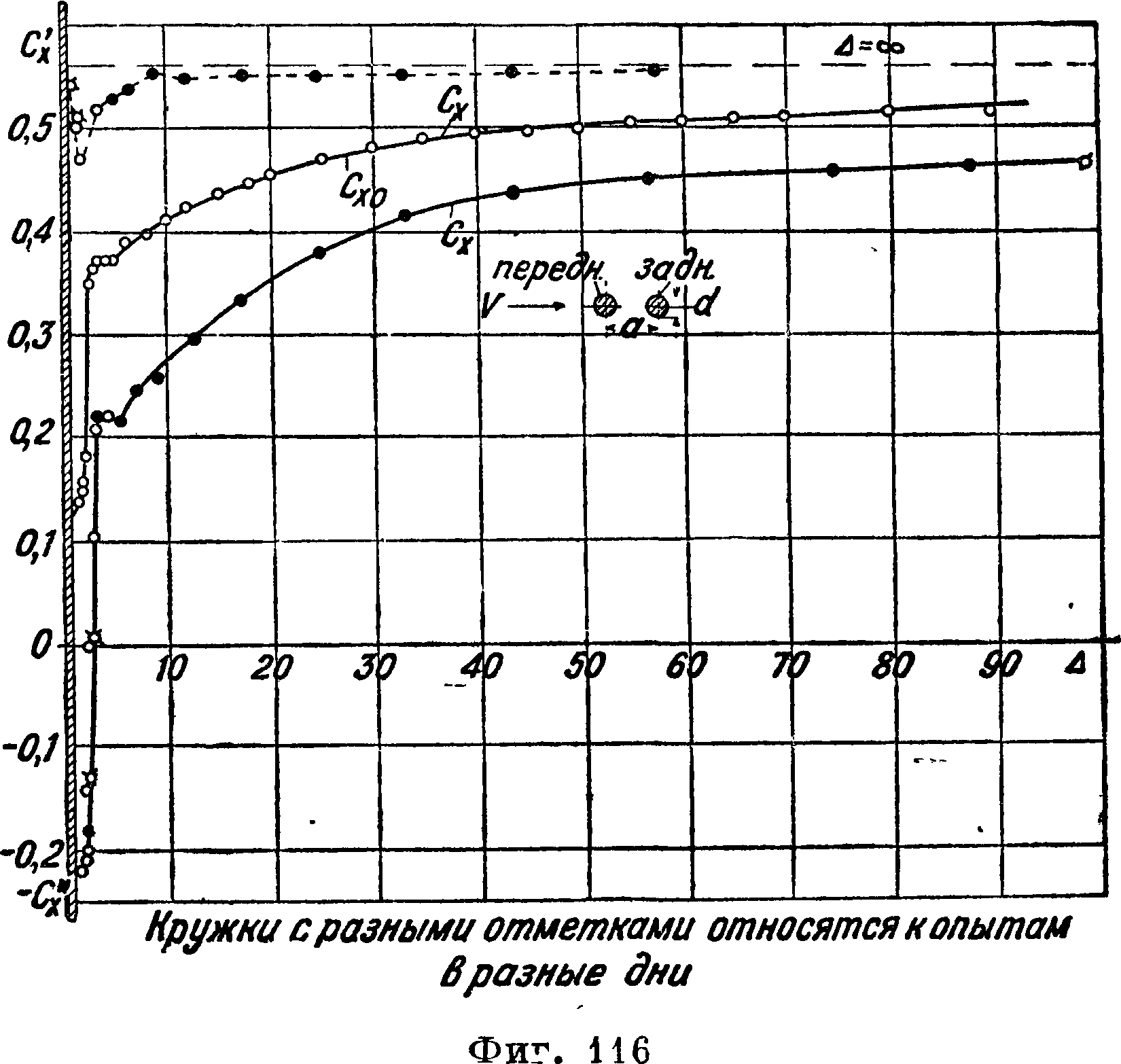
Увеличение сопротивления в этом случае объясняется тем, что при углах а, близких к 90°, между цилиндрами образуется диффузор, увеличивающий обратные токи и интенсивность вихрей.

На фигуре 119 приведены результаты испытания в трубе НК-I МАИ [²²] двух спаренных симметричных стоек. Толщина каждой стойки равнялась 20% от хорды; в таблице 16 указаны координаты профиля испытанных стоек. На фигуре 119 приведена величина коэф-та С_х для каждой из спаренных стоек в зависимости от отношения где h—расстояние между стойками, а — ма-

Фигура 117.

Таблица 16. — Координаты профиля стойки.

Абсцисса В % от хорды	Верхняя и нижняя ординаты в % от хорды	Абсцисса в % от хорды	Верхняя и нижняя ординаты в % от хорды
0,0	0,00	50,0	9,00
3,3	5,00	60,0	7,86
6,6	6,60	70,0	6,20
10,0	7,70	80.0	4,60
20,0	9,46	90,0	2,80
30,0	9,34	93,3	2,13
40,0	9,67	100,0	0,00

ксимальная толщина каждой стойки. Опыты проводились при двух значениях числа Рейнольдса

Re=~ _} где b — глубина стойки. Рассмотрение диаграммы показывает, что по мере сближения стоек коэф. лобового сопротивления возрастает. Возрастание сопротивления объясняется вредным влиянием образующегося между стойками диффузора, вызывающего интенсивное вихреобразова-

ние. При ~<1,15 коэф. лобового сопротивления начинает уменьшаться. Это явление обусловливается тем, что при весьма близких расположениях спаренных стоек они начинают обтекаться как одно целое и за миделевым сечением между стойками образуется мертвая зона, давления в которой равны давлению позади стоек.

Коэф. лобового сопротивления авиационных лент, расположенных тандем и под углом к потоку, м. б. определен путем умножения коэф-та лобового сопротивления изолированной ленты на поправочные коэф-ты, приведенные в таблице 17 [¹⁰].

Таблица 17.—Относительное сопротивление чечевицеобразных лент, расположенных тандем. вые отрезки крыльев были прямоугольной формы, а «ложные» продолжения их прикреплялись к стенкам аэродинамич. трубы с сохранением небольшого зазора между корневыми отрезками и «ложными» крыльями. Такая установка была сделана с целью исключить влияние концов и создать условия обтекания плоско-параллельным потоком, соответствующие бесконечному размаху внешних частей крыла. Ось фюзеляжа устанавливалась по потоку, а угол атаки крыла равнялся нулю. Результаты испытаний приведены на фигуре 122. По оси ординат отложены значения подъемной силы Р в килограммах и лобового сопротивления Q в килограммах фюзеляжа вместе с отсеками, а по оси абсцисс—расстояние крыла от оси

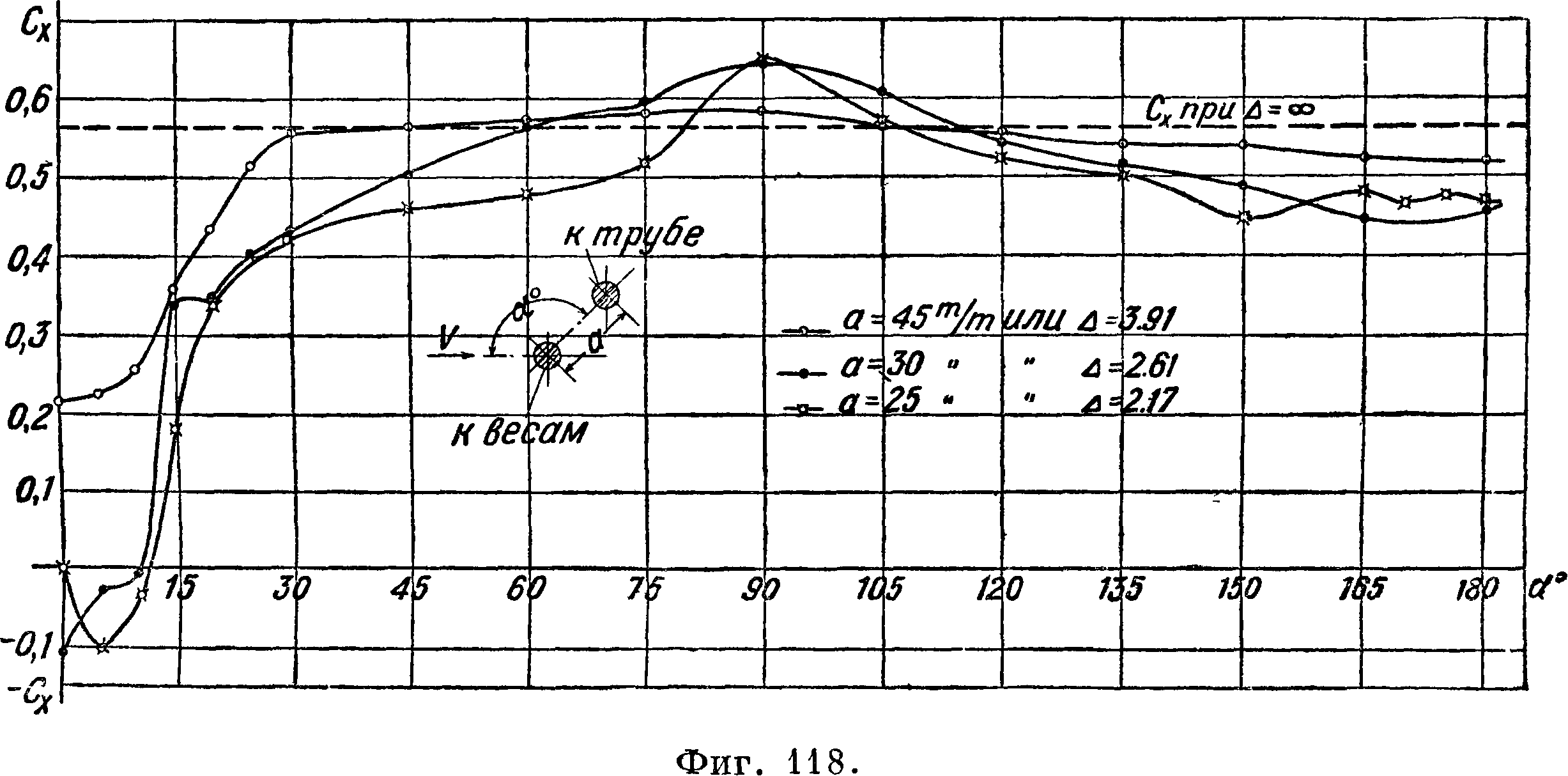
Угол атаки а°	Расстояние между центрами чече-виц, выраженное в максимальных размерах сечения				Относит, сопротивление 2 лент в отдельности
	1	2	3	5
0	0,50	0,86	0,84	0,95	1,00
5	0,69	0,92	0,93	0,97	1,05
10	0,96	1,12	1,63	1,06	1,20
15	1,51	1,12	1,08	1,00	1,69
20	1,11	1,02	1,06	1,02	3,21

Для учета сопротивления концевых креплений спаренных лент на каждую пару лент следует прибавлять по 1,2 метров Учет наклона смотрите выше.

Ь) Интерференция крыла и фюзеляжа. Положительная интерференция крыла и фюзеляжа при неудачном сочетании этих элементов м. б. настолько велика, что приводит, как это было упомянуто выше, к значительному ухудшению ряда основных летных свсшств самолета. На фигуре 120 приведена схематическая модель фюзеляжа, использованная Ower [²³] (Национальная физическ. лаборатория, Англия) для определения наивыгоднейшего расположения крыла относительно фюзеляжа. К модели фюзеляжа прикреплялись отрезки крыла профиля RAF-31. Различные положения отрезков крыла относительно фюзеляжа показаны на фигуре 121. Корне-

фюзеляжа в долях хорды крыла. Для ясности буквами отмечены положения крыла, указан

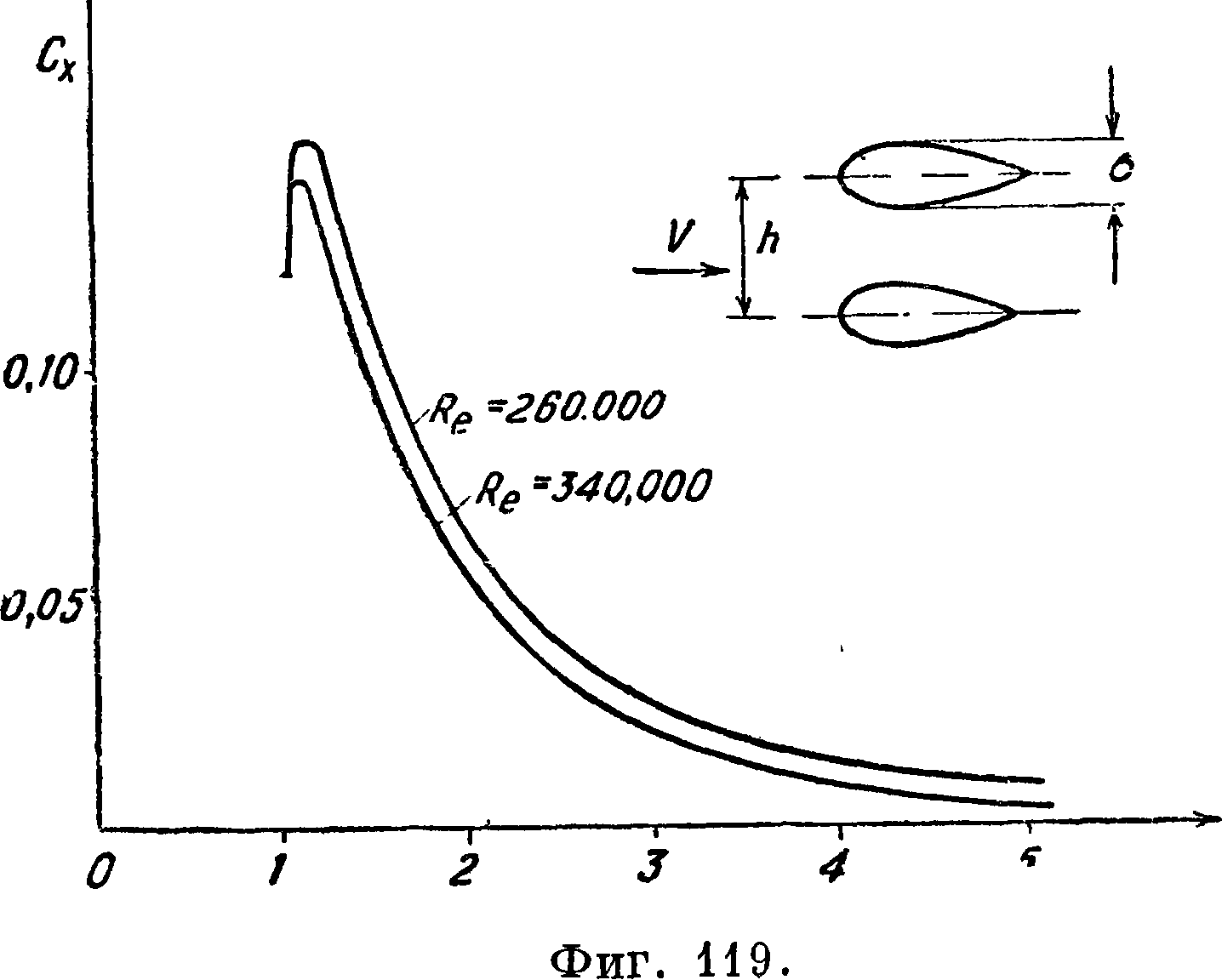
ные на фигуре 121. Положительные значения по оси абсцисс соответствуют положению крыла под осью фюзеляжа. Как видно из фигура 122, наилучшим положением оказалось положение Я, соответствующее помещению крыла посредине фюзеляжа. Наихудшим положением является поло-

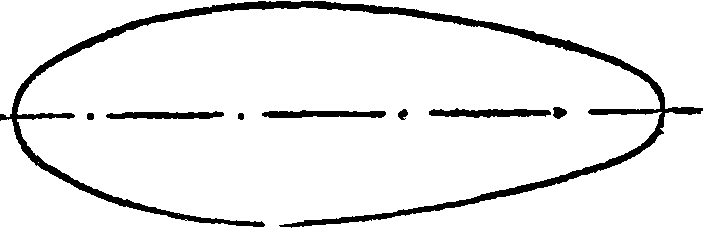
Фигура 120.

Фигура 121.

жение крыла под фюзеляжем (положение М) с небольшим зазором между ними. Положение L, соответствующее самолету с нижним располо-

6

Т. 9. Доп. пг. жением крыла, также является одним из наихудших. Дальнейшие опыты показали, что при нижнем расположении крыла положительное интерференционное сопротивление значительно возрастает по мере увеличения угла атаки. Рассмотренное явление положительной интерференции объясняется образованием диффузора между крылом и фюзеляжем в случае расположения крыла

Фигура 122.

вблизи верхней или нижней поверхности фюзеляжа, что приводит к увеличению положительного градиента давления и следовательно способствует образованию вихрей в рассматриваемых местах и в результате приводит к срыву потока с поверхности крыла и фюзеляжа. Это явление особенно резко выражено при нижнем расположении крыла (положения L и М), т. к. в этом случае вызывающий срыв потока поло

жительный градиент на задней части верхней поверхности крыла еще усиливается диффузором, образующимся между крылом и фюзеляжем. Для устранения диффузора область между крылом и фюзеляжем закрывают обтекателем, называемым «зализом». Этим путем удается значительно уменьшить положительную интерференцию, а при удачной форме зализа свести ее к нулю. На фигуре 123 приведена зависимость между уве личением подъемной силы и радиусом зализа в долях хорды, а на фигуре 12* дана зависимость

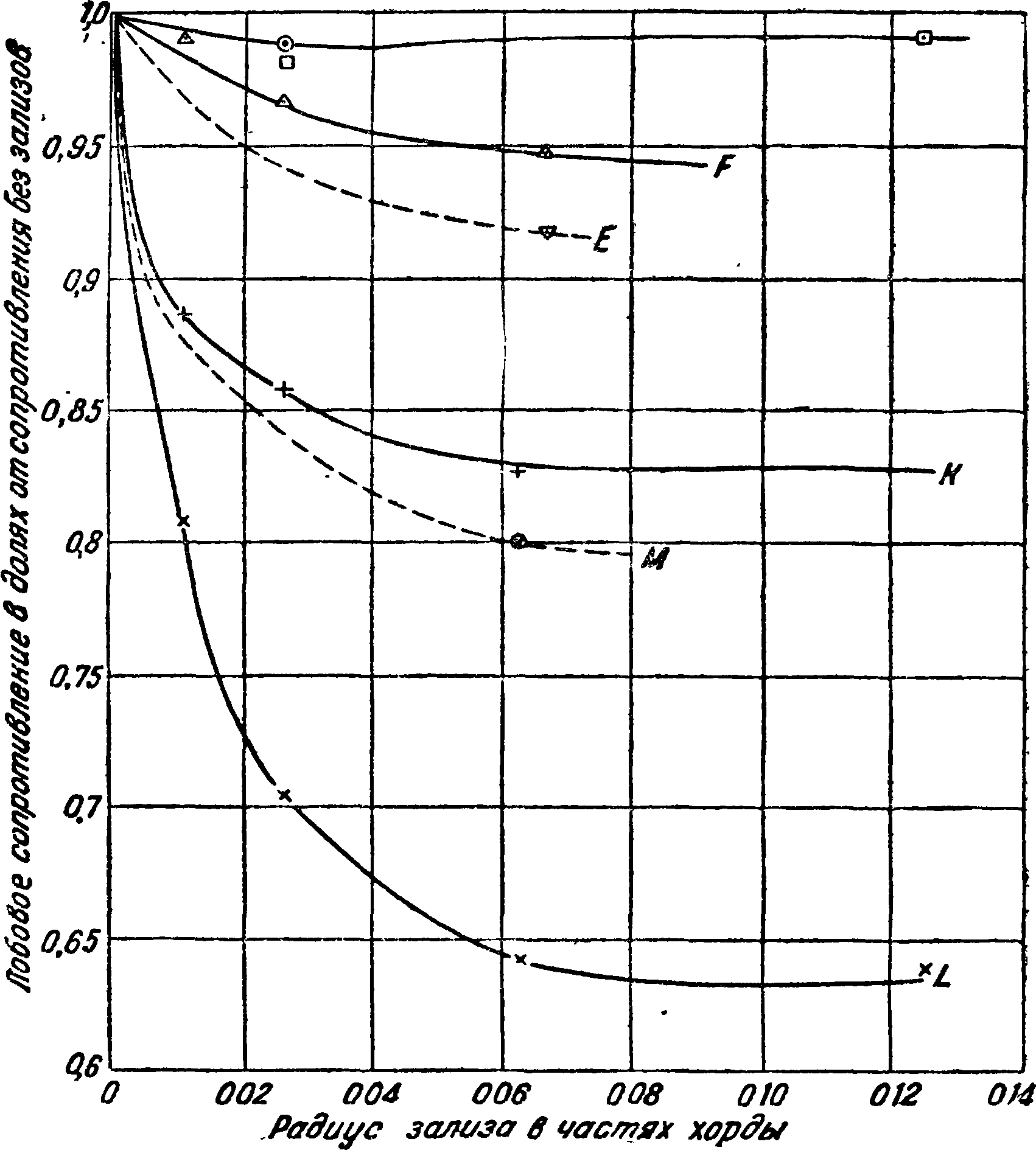
Фигура 124.

между уменьшением лобового сопротивления и радиусом зализа. Наилучший радиус зализа по опытам Ower равен б — 8% от хорды крыла.

На фигуре 126 приведены результаты опытов, проведенных в Геттингенской аэродинамич. лаборатории (Германия) [²⁴,²⁵] с рядом схематич. моделей фюзеляжей, изображенных на фигуре 125.

Фигура 125.

На фигуре 126 приведены поляры Лилиенталя изолированного крыла и крыла с четырьмя фюзеляжами, боковые поверхности которых составляли с верхней поверхностью крыла углы, равные 120, 90, 60 и 45°. При углах 120 и 90° положительная интерференция невелика, наоборот,

при острых углах, равных 60 и 45°, когда между верхней поверхностью крыла и фюзеляжем образуется диффузор, положительная интерференция намного больше, причем она растет с уменьшением угла между фюзеляжем и крылом и с увеличением угла атаки.

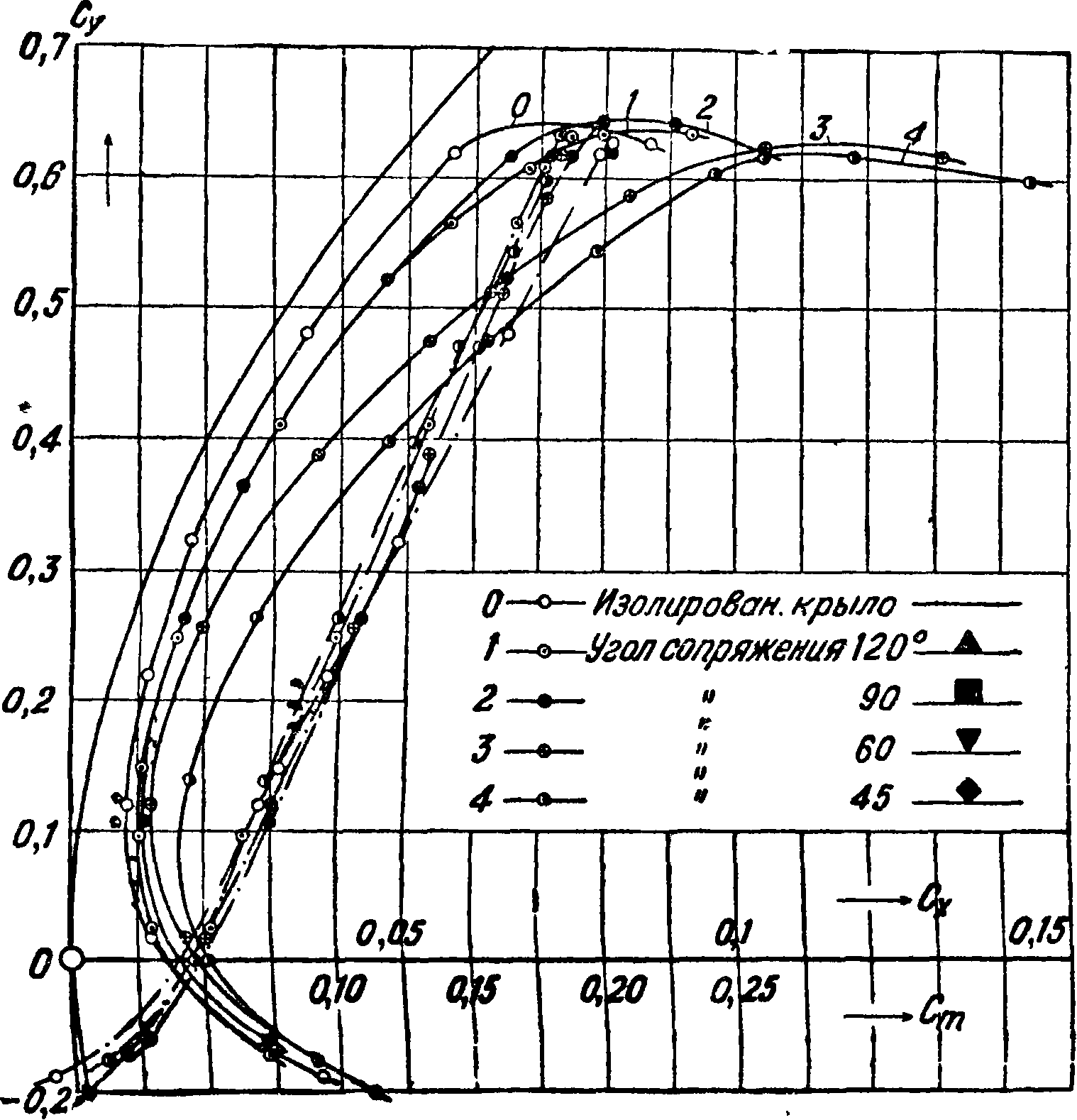
Фкг. 126.

Подробные опыты по изысканию наивыгоднейшей формы зализа для нижнего расположения положений, крыла. Опыты проводились с моделью самолета «Нортроп альфа» в Аэродина-мич. лаборатории Калифорнийского технологии, ин-та [²⁶]. На фигуре .128 приведены поляры Лилиенталя и кривые С_у по а° для изолированного крыла, крыла с фюзеляжем без зализа, крыла с фюзеляжем при неправильном зализе и при наивыгоднейшем зализе. Рассмотрение диаграммы показывает, что при наивыгоднейшей форме зализа положительная интерференция отсутствует и лобовое сопротивление крыла увеличивается только на лобовое сопротивление фюзеляжа. Анализ радиусов кривизны в различных точках наивыгоднейшего зализа показывает, что вблизи передней кромки радиус зализа равен 1,5% от хорды крыла, далее он возрастает; в области максимальной толщины радиус зализа равен 5—8% от хорды крыла, а вблизи задней кромки он достигает 27,5% от хорды. Часть зализа, расположенная за задней кромкой крыла, приподнята вверх и, постепенно уменьшаясь, плавно сходит нанет. При таком зализе диффу-зорный эффект отсутствует. Зализ с большим радиусом кривизны вблизи передней кромки и с малым радиусом кривизны вблизи задней кромки дает неудовлетворительный результат, так как такой зализ ’ не устраняет диффузорного эффекта. с) Интерференция крыла и моторных гондол. На фигуре 129 —131 показаны схемы различных положений моторной гондолы относительно крыла, а в таблице 18 приведены результаты испытаний в Аэродинамич. лаборатории в Фарнборо (Англия) Г ³⁰]. Рассмотре-

крыла были проведены в США [²⁶, ²⁷]. На фигуре 127 приведены формы неправильного зализа и двух наивыгоднейших зализов для двух ние табл. 18 показывает, что наименее выгодным оказывается положение А моторной гондолы над крылом на расстоянии 0,62 ее диаметра.

Наивыгоднейшим положением является положение By когда носик гондолы находится на хорде крыла, а сама гондола помещается частично

Таблица 18.—Отношение сопротивления изолированной моторной гондолы плюс интерференция к сопротивлению изоли-рованной гондолы (профиль RAF=34, α=6, хорда 5=0,203 м, скорость

υ=18,3 м/ск).

Фиг. и № кока	Абсцисса носика гондолы в диам. кока	Ординаты носика гондолы в диам. гондолы	Угол атаки а
			1°	2,6°	5,2°	6,3°	10,1°	14,4°	16,4°	18°
59 A	1,07	0,62	3,00	4,91	7,39	8,15	13,30	15,37	15,10	16,05
60 Б	1,07	0,33	1,16	1,58	1,99	2,16	6,53	13,00	13,54	23,95
61 В	1,07	0,00	0,84	0,89	0,83	0,89	1,68	3,96	15,76	26,10

над крылом, а частично под крылом. На фигуре 132 приведены соответствующие этим случаям поляры Лилиенталя. Сравнение их с полярой Лилиенталя изолированного крыла по-с_у называет на значительную положитель ную интерференцию при расположении

0,6^:

о,5

ОА

0,5

о,г о

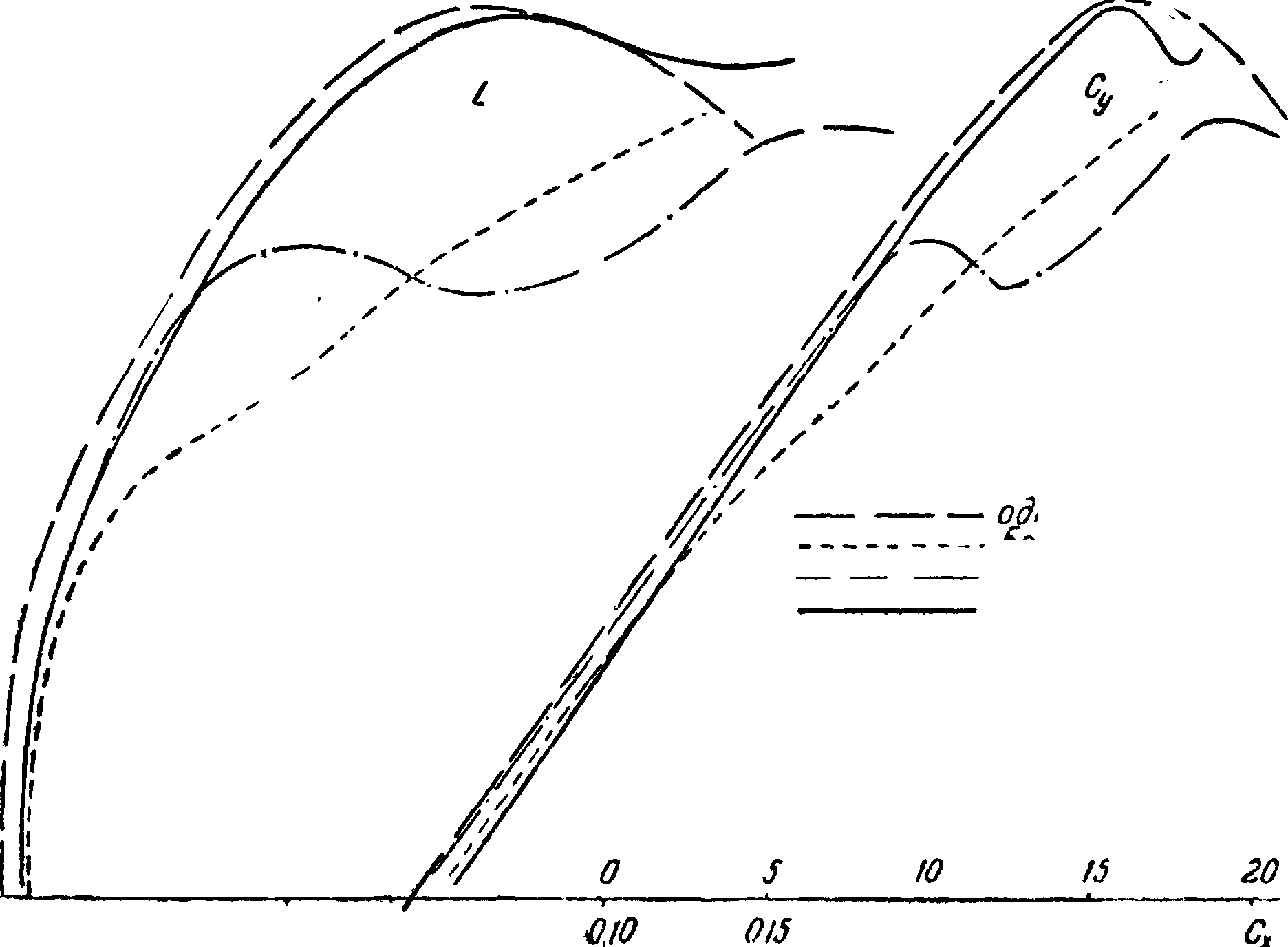
0.05

Фигура 128.

моторной гондолы над крылом и на почти полное отсутствие положительной интерференции при расположении гондолы в крыле. Опыты, проведенные в большой трубе (диам.=6,1 м) Аэродинамической лаборато-Л рии в Ланглейфильде

(США) [³¹] с работающим винтом, подтверждают этот вывод. Из болыно-го числа исследованных случаев наилучшим оказалось положение гондолы в крыле при расстоянии плоскости вращения винта от передней кромки крыла, равном 0,25% от хорды [²³, ^за|. А., Применение обтекателей

Фигура 129.

Лит.: !) Мартынов на моторах воздушного охлаждения для уменьшения лобового сопротивления фюзеляжей, «Техника воздушного флота», 1932, 4; 2) Румянцева Е., Атлас лобовых сопротивлений ненесущих частей самолета. Испытание фюзеляжей и лодок, «Труды ЦАГИ», ISO; 3) Щербаков

К., Аэродинамич. исследования шасси самолетов и изолированных колес, там же, 196; 4) Чев А., Коэфициенты вредных сопротивлений по аэродинамич. расчету самолетов, там же, 1929, вып. 42; 5) Кузнецов Б., Лобовое сопротивление тросов, проволок тан-деров и авиационных лент, там же, 1930, вып. 97; 6) Горский В., Аэродинамич. исследования горизонтальных оперений с компенсаторами и без них. Аэродинамические исследования по оперению самолета, там же, 1930, вып. 49; ЧРумянцеваЕ., Аэродинамич. исследования изолированных горизонтальных оперений, «Технич. замки ЦАГИ», 1932, 1; 8) Румянцева Е., Влияние геометрич. параметров на аэродинамич. характеристики изолированных горизонтальных оперений, там же, 1929, 42; 9) Ведров В.,

Скос потока у стабилизатора. Материалы по аэродинамич. расчету самолетов, «Труды ЦАГИ», 1929, вып. 42; Ю) Горский В., Влияние обдувки на фюзеляж и хвостовое оперение самолета Ц-2, «Технич. заметки ЦАГИ», 1932, 1; и) Могилев ский М. и О с т о с л а в с к и и И., Исследование скоса потока у оперения самолета, «Техника воздушного флота», 1930, 10; 12) Горский В., Исследование влияния фюзеляжа на горизонтальное оперение самолета. Аэродинамич. исследования по оперению самолета, «Труды ЦАГИ», 1930, вып. 49; 13) Ж у р а в ч е н к о А., Экспериментальные поправки на интерференцию фюзеляжа и оперения. Аэродинамические исследования по оперению самолета, там же, 1930, вып. 49; Ы) Гончаров Б., Подбор органов управления самолета, «Технич. заметки ЦАГИ», 1934, 34; 15) К у з н е ц о в Б., Аэродинамич. исследования цилиндров, «Труды ЦАГИ», 1931, вып. 98; 16) Федя е в с к и и К., Влияние расстояния между стойками на их лобовое сопротивление, «Техника воздушного флота», 1931, 4; 17) Muttra у Н., Исследование влияния фюзеляжа на крыло при верхнем положении фюзеляжа (реф. Ф. Гласса), «Техника воздушного флота», 1929, 7; 18) Румянцева Е., Взаимное влияние крыла и фюзеляжа, «Технич. заметки ЦАГИ», 1934, 36; 1») Резунов М., Влияние надстроек на верхней поверхности крыла на его аэродинамич. характеристики, «Труды ЦАГИ», 1931, вып. 86; 20) Prace Insty-tutu Aerodynamicznego w Warszawfe, Zeszyt 5, Warszawa, 1932; 2i) Modell-messungen uber die zweckmassigste Aus-bildung der Sitzausschnitte in offenen Flugzeugen, «Bericht aus dem Aero-dynamischen Institut der technischen Hochschule Aachen», Luftfahrtforschung, Mch.—B, 1924, B. 11, 3; 22) w e i k F., with Various Forms of Cowling for a Engine-I, «Technical Re-

¹ крыло uej зализа с не прабилькым зализом С май выгоднейшим зализом

Drag and Cooling, _4Λ, «Whirlwind», Radial Air-Cooled

port NACA», 313; with Various Forms of Cowling for a «Whirlwind», Radial Air-Cooled Engine-II, ibid., 314; 24) N о r t h J., Air-Cooled Engine Cowling, «Aircraft Engineering», 1934, April; 25) a r e e n F., The Resistance of Air-Cooled Engines, «The Journal of the Royal Aeronautica Society», 1930, 238; 26) О w e r E., Some Aspects of the Mutual Interference between Parts of Aircraft, «Aeronaut. Research Committee, Rep. and Mem.», 1932, 1480; 27) M ut tray

W e i k F., Drag and Cooling

Фигура 130 и 131.

„ H., Versuche uber die Ausbil-dung der Flugelwurzel von Tiefdeckern, «Ergebnisse der Aerodynamischen Versuchsanstalt zu Gottingen», Lfg 4, 1932; 28) Klein A., Effect of Fillets on Wing-Fuselage Interference, «Transactions of the American Society of Mechanical Engineers», N. Y., 1934, y. 56,

January, 1; Щ M a η 1 e у J., Η ο ο d a n d White J., Full-Scale Wind Tunnel Research on Tail Buffeting and Wing-Fuselage Interference of a Low-Wing Monoplane; so) H a r t s c h o r n A., The Influence of a Fuselage on the Lift of a Monoplane, «Aeronautical Research

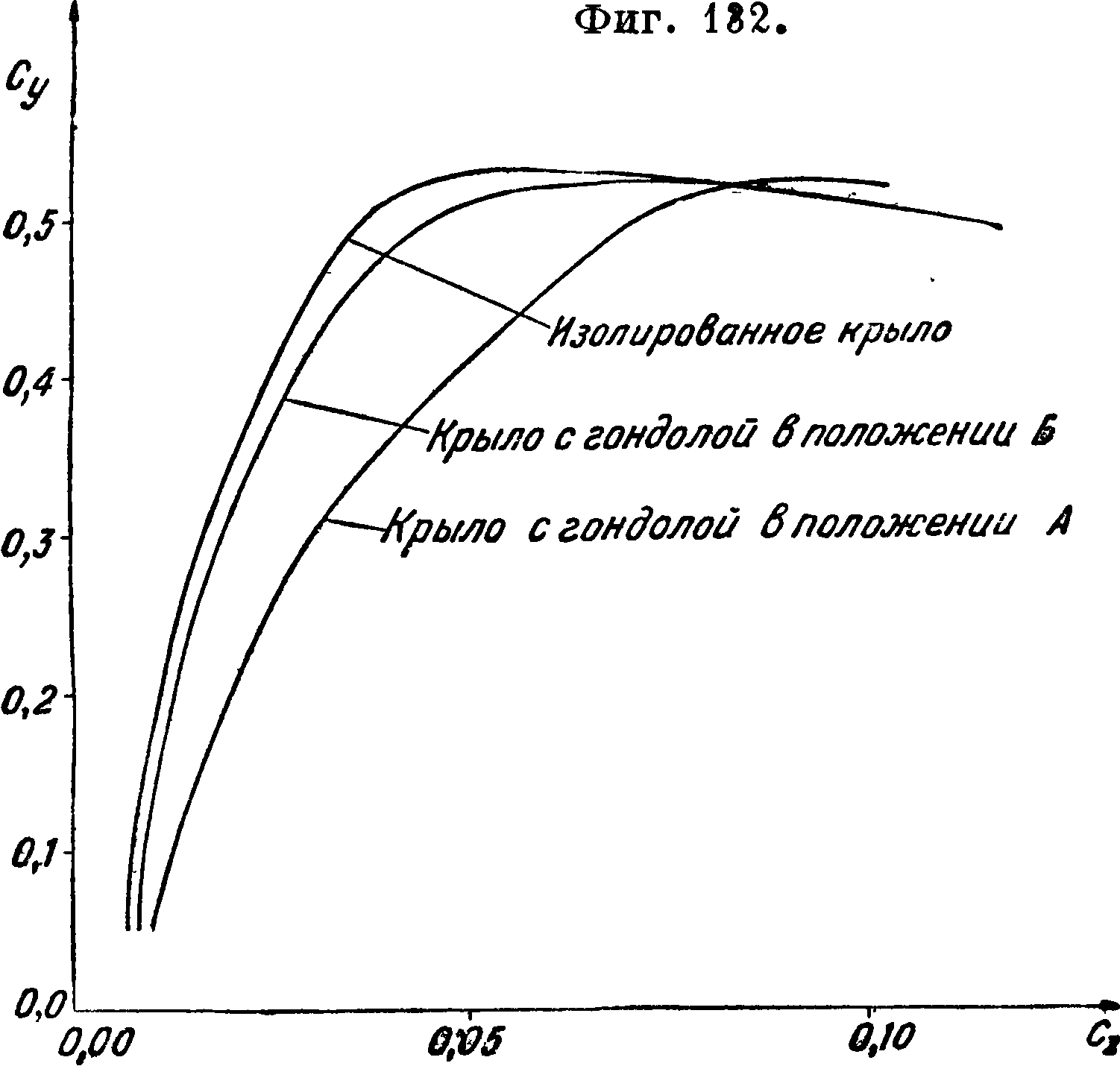
выраженная в процентах, равна В каче стве типичного материала f¹] приводим три диаграммы, относящиеся к испытаниям эталонного крыла в лаборатории Московского авиационного ин-та. На фигуре 133 приведены кривые относительных (100Δ С_х/С_х) и абсолютных (&С_Х) ошибок в ф-ии угла атаки а для коэф. лобового сопротивления С_х. На фигуре 134 аналогичные кривые даны

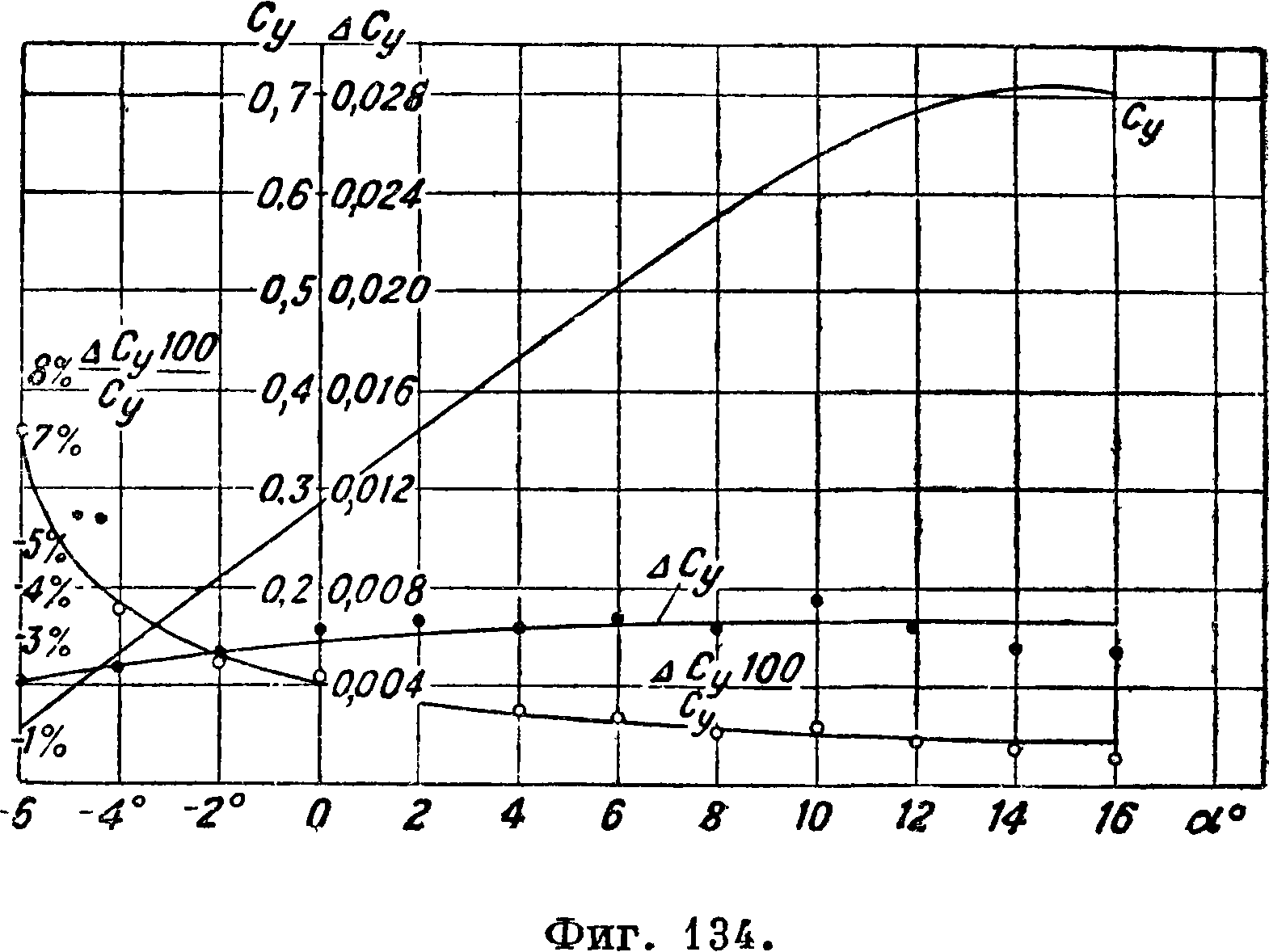
Committee, Rep. a. Mem.», 1344; si) Perring W. and C alien C., Drag and Interference of a Nacelle when installed on the upper Surface of a Wing, ibid., 1932, 1414; 32) Donald H. W о о d, Tests of Nacelle Propeller Combinations in Various Positions with Reference to Wings, «Techn. Report NACA», 415. П. Красильщиков.

X. Точность аэродинамических исследований.

При повторных испытаниях одной и той же модели в аэродинамич. трубе всегда имеют место довольно заметные расхождения, причины к-рых, вообще говоря, весьма разнообразны и трудно устранимы. Оценка порядка величины этих расхождений имеет существенное значение, т. к.

результаты аэродинамических исследований кладутся в основу расчетов различных летательных аппаратов. В практике многих лабораторий принято оценивать точность эксперимента по результатам многократных испытаний т. н. эталонных крыльев. Обработка этих результатов по теории ошибок дает весьма наглядное представление о точности аэродинамич. исследований. Известно, что вероятнейшее значение некоторой величины равно среднему арифметическому из отдельных измерений, а порядок ошибки отдельного измерения м. б. характеризован величиной ε, т. н. «средней квадратич. ошибкой», вероятнейшее значение которой вычисляется по ф-ле

•=±УЩΨ-.

где х — величина среднего арифметического, —значение отдельного измерения, п—число всех измерений. Относительная средняя ошибка,

для коэф-та подъемной силы С_у. Заштрихованные области на фигуре 135 построены т. о., что верхняя

кривая каждой области соответствует значениям ic+ε, а нижняя кривая—значениям ε. Веро ятность того, что при отдельном испытании измеренные величины не выйдут за пределы заштрихованных областей, составляет 0,75.

Лит.: 1) Ушаков Б., Повторные испытания ме-таллич. крыла в трубе НК-1, «Труды I Всесоюзной конференции по аэродинамике», М., 1932, стр. 28—32;

Красильщиков П., О точности аэродинамич. испытаний, «Труды ЦАГИ», 1931, вып. 65; Кожевников А., Сравнительные испытания одного и того же ме-таллич. крыла и шара в аэродинамич. трубах СССР и за границей, «Труды I Всесоюзной конференции по аэродинамике», М., 1932, стр. 46—62; Баулин К., Обзор работ винтовой секции ЭАО ЦАГИ, там же, М., 1932, стр. ИЗ—120; «Ergebnisse der Aerodyn. Versuchsanstalt zu Gottingen», Lfg 1, p. 48—49. Б. Ушаков.

XI. Измерение скорости воздушного потока. а) Трубки Пито. Одним из наиболее простых и удобных приборов для измерения скорости воздушного потока является т. н. трубка Пито, при помощи которой можно определить разность между полным и статич. давлением в потоке, а из величины этой разности можно найти и значение скорости. В основе этого метода лежит ур-ие Бернулли, к-рое для воздуха (рассматриваемого как несжимаемая, невесомая и невязкая жидкость) м. б. представлено в виде

Po + ej=Pi + ej=е, (1)

то есть другими словами полное давление, равное сумме статич. и динамич. давления, остается постоянным вдоль линии тока. Если линия тока встречает препятствие, то скорост > обращается в нуль, и давление, испытываемое этой точкой тела, будет равно пэлному давлению в потоке,

то есть

Отсюда и

Ρι =	= Ро + е ^ ·	(2)
4-	-Pi Ро = ^	(3)
	-V*·	(4)

Т. о. если мы сможем найти разность h между полным и статич. давлением в потоке, то скорость v₀ невозмущенного потока м. б. определена из ф-лы (4). рубка Пито, различные типы которой представлены на фигуре 136—139, позволяет как-

раз определить эту разность h: переднее ее отверстие, обращенное против направления потока, испытывает со стороны последнего полное давление, а отверстия в боковых ее стенках находятся под воздействием статического давления,

т. к. скорость здесь направлена вдоль стенок и по величине весьма близка к скорости ν_ύ невозмущенного потока. Соединив эти отверстия при помощи трубок с двумя концами жидкостного микроманометра, мы получим величину h, измеренную обычно в миллиметров вод. ст., что очевидно со ответствует давлению, выраженному в килограммах/м². Различные виды трубок [на фигура 136—стандартная трубка Пито-ЦАГИ (1-й вариант) при d — 2,4; 4, 6 и 8 миллиметров на фигуре 137—стандартная трубка Пито-ЦАГИ (2-й вариант) при d=2,4; 4,6 и 8 миллиметров на фигуре 138—трубка Пито-Прандтля; на фигуре 139—трубка Пито-Браббэ (трубки этого типа при

меняются в лабораториях Англии и США)] отличаются в основном формой головки, положением отверстий статич. давления и расстоянием последних от державки. Полное давление измеряется трубкой Пито практически совершенно точно, и основная трудность заключается в правильном замере статического давления, так как неудачное положение отверстий статического давления и неправильно установленное расстояние державки могут существенным образом исказить результаты.

На фигуре 140 представлены 4 вида головок [⁸]: трех конических разной длины а, б, ей одной полусферической г, присоединявшихся к полой дренированной трубке д. Так как головки были просверлены не насквозь, то в полости трубки господствовало то давление, под которым находились открытые для данного опыта отверстия (в каждом сечении их было 4). На фигуре 141 представлены распределения давления вдоль трубки для различных видов головок при отсутствии державки. По оси абсцисс отложены расстояния сечений от основания головки, выраженные в диаметрах трубки, & по оси ординат разности в процентах от скоростного напора между измеренным давлением у данного сечения и истинным статич. давлением в потоке р_изли—р_ист. · Из диаграммы следует, что при желании наиболее правильно измерить статическое давление с помощью такой трубки без державки отверстия статич. давления должны находиться не ближе 6 диам. от основания головки независимо от формы последней. Но и в этом случае измеренное статич. давление будет меньше статич. давления в потоке примерно на 0,25% от скоростного напора. Присутствие державки однако существенно меняет дело, так как вносимый ей подпор повышает статич. давление у сечений. На фигуре 142 представлена .кривая повышения давления у сечения, отстоявшего на 12Z) от основания головки, при различных расстояниях, от него державки для трех типов головки. Форма головки и на этот раз не оказывает большого влияния, и существенное значение имеет только расстояние державки от отверстий статич. давления. Отсюда видно, что при правильном выборе положения державки пониженное против статического давление у данного сечения можно повысить как-раз до требуемой величины. В большинстве практич. трубок Пито эта задача решена вполне удовлетворительно. Тем не менее каждая из них нуждается в специальной тарировке для определения своего поправочного коэф-та, хотя он обычно и очень близок к единице.

Трубка Пито обладает довольно слабой чувствительностью к направлению потока [⁷], т. ч. отпадает необходимость устанавливать ее строго

Фигура 140.

по потоку. В некоторых случаях, при затруднительности определить действительное направление потока, это обстоятельство представляет серьезное преимущество. На фигуре 143 приведены для насадка типа Прандтля три кривые, представляющие изменение полного напора р, статич.

J

1

I

ft

*1

I

I *

--1 и Ρψ
~jfr щ
	о Трубка Пито - а×в + * 6 *
			i
’1 —_ —.

^ о г 4 6 8 10 12 14 16

Расстояние сечений от основания гол о в ни (6 ф трубки]

Фигура 141.

давления р_с и скоростного напора при от клонении оси трубки от направления потока. Полное давление и статич. давление при отклонении уменьшаются, но их разность, равная скоростному напору, остается почти постоянной в пределах ±2°. Насадки с конич. головкой обладают несколько большей чувствительностью к направлению потока. Сжимаемостью воздуха можно пренебрегать до скоростей порядка 70—100 м/ск, т. к. величина ошибки в определении скорости не превысит 1 — 2%. При скоростях выше 100 mJck и скоростях выше скорости звука [⁴] необходимо применять особые ф-лы.

b) Измерение скорости в пульсирующем потоке [⁵]. Т. к. при помощи трубки Пито мы определяем среднюю величину скоростного напора, то есть величину, пропорциональную квадрату скорости, то при измерении трубкой Пито средней скорости в пульсирующем (турбулентном) потоке мы можем найти среднее квадратическое, а не среднее арифметическое значение скорости. Т. к. среднее арифметическое всегда несколько меньше среднего квадратического, то для турбулентного потока мы получим всегда несколько преувеличенное значение скорости. По опытам Кумбруха [⁶] в сильно тур-булизированном потоке поправочный коэф. к скоростному напору может измениться примерно на 4%, то есть измеренное значение скорости может оказаться на 2% больше действительной средней ее величины. В аэро-динамич. трубах степень турбулентности однако значительно меньше, и разница между средней скоростью, полученной с помощью трубки Пито, и действительной средней скоростью измеряется только долями процента и в расчет обычно не принимается.

c) Измерением а-лыхскоростей [⁸].

Т. к. при стандартных условиях (давление 760 миллиметров рт. ст. и t°=15°) ρ=0,125 килограмм-ск²/м⁴, то из ф-лы (4) следует, что

v₀=YWh=iVh. (5)

Если h=1 миллиметров вод. ст. =

= 1 килограмм/м², то Vq=4 м/ск.

Точное определение давления

I!¹

it

	—i—г 1 I
	Трубка Пито в • г
Т
i
		V
					Ч-

- S 10 15 20 25 30

Расстояние дфжавки от отверстия статич. давления ίβ а™)

ФИГ. 142.

ВОД. %от ϋ

-20

ст. с помощью обычных порядка 1 миллиметров микроманометров

-40

-SO

•SO

-too

V*- 2		- |-	_
	Jf			V^
	f			А
	у
					п

-40 -го

20

40 SO⁹

-

Фигура 143.

крайне затрудаительно, поэтому нижний предел надежного определения скорости потока с помощью трубки Пито и обычного микроманометра ограничивается величинами порядка 8—10 м/ск. Но при применении специальных особо чувствительных микроманометров трубкой Пито можно измерить и очень малые скорости порядка 0,6 м/ск. Если в ур-ии

kh=_t

_V2

(6)

поправочный коэф. к при обычных скоростях потока постоянен и близск к единице, то при малых скоростях величина его заметно меняется. На фигуре 144 дана кривая значений коэф-та к стандартной трубки Пито Нацио-

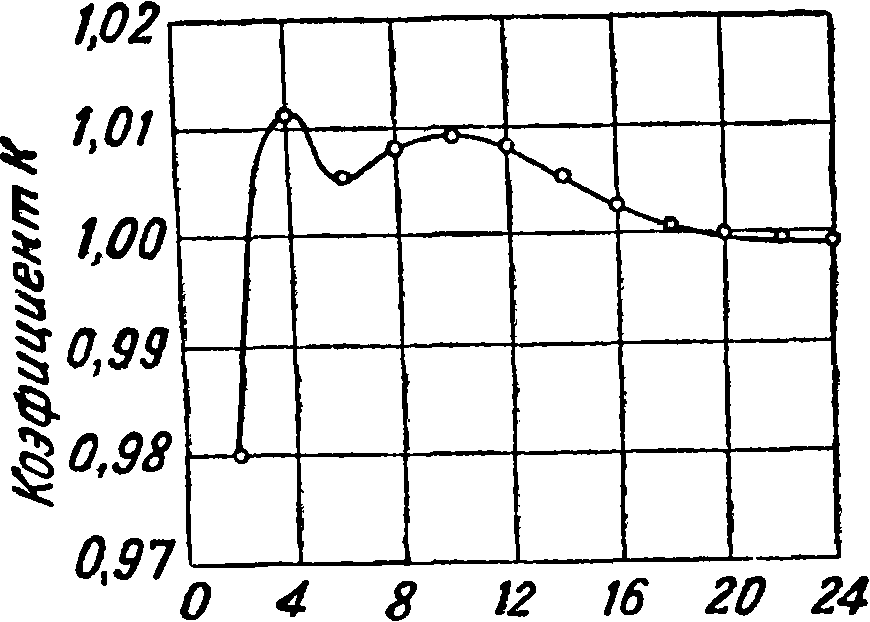
Скорость потока вр т/сек Давление 760мм pm cm г-ра15°

Фигура 144.

нальной физич. лаборатории по опытам Ower, проводившимся в диапазоне скоростей 24-24 фт/ск. (0,614-7,3 м/ск). Ограничиваясь скоростями от 4 фт/ск. и выше, видим, что изменение коэф-та к равно примерно 1%. Пренебрегая этим изменением к и счи-к при обычных скоро тал его равным значению. ^

стях, мы сделаем ошибку в определении скорости не свыше 0,5—0,6%, чем в большинстве слу чаев можно пренебречь.

d) Определение направления скорости воздушного потока[ ², ³, ⁷, ⁹,¹⁰]. В ряде случаев необходимо знать не только величину, но и направление скорости воздушного потока. Трубка Пито, как мы видели, для этой цели не пригодна, и вместо нее применяются особые насадки. На фигуре 145 представлен т. н. ци-линдрич. насадок. У конца трубки в одном поперечном сечении сделаны три отверстия, схема соединений которых с манометрами дана на той же фигуре. Если отверстия а и b будут расположены симметрично относительно направления потока, то уровни в обоих коленах 11-образного манометра будут стоять на одной высоте. Обычный микроманометр служит для измерения скоростного напора, причем величина поправочного коэфициента определяется из особой тарировки.

Поворотом цилиндрич. насадка около его продольной оси можно всегда добиться совпадения уровней и определить угол, составляемый направлением потока с некоторой фиксированной плоскостью. На фигуре 146 представлен т. н. английский насадок, принцип работы которого аналогичен принципу работы цилиндрич. насадка. Так как указанные два насадка дают возможность определить только положение проекции вектора скорости на плоскости, перпендикулярной к оси насадка, то применяются ещет. н. пространственные насадки. Первый из них получается из английского насадка путем добавления второй пары согнутых трубочек, плоскость которых перпендикулярна к плоскости первой пары. Каждая пара^ трубок соединяется со своим U-образным мано-**

метром. Вращая насадок сначала около оси, перпендикулярной одной из этих плоскостей, а затем около другой, всегда можно добиться совпадения уровней в обоих U-образных манометрах. Зная углы поворота около каждой оси, можно найти действительное пространственное положение вектора скорости в данной точке. Аналогично протекает работа с шаровым насадком, схематич. вид которого приведен на фигуре 147.

е) Электрический метод измерения скорости потока [⁷, ⁸, ⁹, ⁿJ. За последнее время электрический метод измерения скорости воздушного потока (т. наз. термоанемометрия) получил широкое распространение в практич. работе аэродинамич. лабораторий, особенно заграничных. Этот метод основан на изменении электрич. сопротивления нагретой тонкой проволоки при охлаждении ее потоком воздуха. Материалом для проволоки служат платина или никель благодаря их химич. инертности к атмосферным условиям даже при высокой ί°. Кроме того электрич. сопротивление платины и никеля сильно зависит от ί°, что в данном случае и требуется. Т. к. платина допускает нагрев до более высокой t°, то применение ее предпочтительнее. Типич. форма насадка приведена на фигуре 148: а—тонкая платиновая нить (диам.

0,01—0,1 миллиметров, длина 2—30 миллиметров); б и в— манганиновые державки, укрепленные на эбонитовой подставке г. Подставки вделаны в металлич. трубку д, внутри которой идут провода е от державок б и в Тщательность контактов между

проволокой а и державками б ж в имеет чру крайне существенное значение. Реко- у · мендуется применять здесь сварку, a h v не пайку. Проволоку а можно устана- _{Фиг 148>}вливать или перпендикулярно или параллельно направлению потока. Измерение скорости потока можно делать при помощи самых разнообразных электрич. схем, из которых приведем две наиболее типичные.

1) Метод постоянного напряжения (фигура 149). Насадок Я является одним из плеч мостика Уитстона. При отсутствии потока сила тока регулируется реостатом R так, чтобы гальванометр G находился на нуле. При набегании потока проволока начнет охлаждаться, и равновесие мостика нарушится. Стрелка гальванометра отклонится тем больше, чем больше охладится проволока, то есть чем больше скорость потока. Т. о. по отклонению стрелки гальванометра можно найти скорость потока. Этот способ пригоден только для очень малых скоростей (от нескольких см/ск до 4—5 mJck), т. к. при дальнейшем повышении скорости потока охлаждение проволоки почти не увеличивается, а следовательно и сопротивление ее почти не меняется. Тарировку этого насадка лучше всего делать на ротативной машине.

2) Метод постоянной температуры нити (фигура 150). Измеряемый диапазон скоростей для этого метода составляет примерно от 0,5 до 10 —12 м/ск. Стрелка гальванометра G

должна все время в потоке и без потока стоять на нуле, что достигается соответствующей регулировкой силы тока, нагревающего нить. Равновесие мостика очевидно возможно только в том

случае, если сопротивление нити, а следовательно и ее t° будут оставаться постоянными. Величина сопротивлений в остальных плечах мостика меняться при этом не будет, т. к. все сопротивления делаются из манганина, температурный коэф. которого практически равен нулю. Скорость потока можно представить или в функции показаний амперметра А или вольтметра V. Если скорость потока превысит 12 .ю/ск, то количество тепла, теряемого проволокой, будет расти крайне медленно, и увеличивать силу тока в мостике для сохранения его равновесия почти не потребуется. Т. о. точность измерения скорости при повышении ее быстро падает, а скорости, превышающие 12 ж/ся, оказываются практически неопределимыми. При некоторых видоизменениях этой схемы (а также в некоторых других схемах) можно однако добиться почти прямолинейной тарировочной кривой, допускающей измерение скоростей потока до величин порядка 50—70 м/ск. Комбинированные насадки, состоящие из нескольких проволок, позволяют наряду с величиной скорости определить и ее направление. Основное преимущество метода термо-аиемометриц заключается в почти полной его безинерционности при малом диам. нити. Это свойство позволяет применять термонасадки для изучения пульсаций скорости потока. Т. к. размеры насадка м. б. очень малыми, то становится возможным самое детальное исследование структуры потока [¹², ¹³, ¹⁴, ¹⁵, ¹⁶].

Лит.: 1) Юрьев Б. и Лесникова Н., Аэроди-намич. исследования, «Труды ЦАГИ», М., 1928, вып. 33; 2) Красноперов Е., Экспериментальная аэродинамика, ч. 1, М., 1930; 3) Александров В., Тех-нич. гидродинамика, М.—Л., 1932; ⁴) О к у н е в, Шапиро и Венцель, Внешняя баллистика, Л., 1933; 5) В airstow L., Applied Aerodynamics, L., 1920; β) Kumbruch H., Messung stromender Luft mittels Staugeraten, «Forscbungsarbeiten auf d. Gebiete des Ingenieurwesens», B., 1921, H. 240; ⁷) P r a n d t 1-T i e t-j ens, Hydro- u. Aeromechanik, B. 2, B., 1931; 8) О w e r F., Measurement of Air Flow, L., 1933; *) Ilndb. d. Expe-rimentalphysik, hrsg. v. W. Wien u. F. Harms, B. 4, T. 1, Hydro- u. Aerodynamik, Lpz., 1931; ^la) В u k о w s-k i i J., Technika laboratoryjna pomiarow aerodynamicz-nych, Warszawa, 1933; H) Ulsamer Л., Die Grund-lagen der Messung der Geschwindigkeit nach Grosse u. Richtung mit d. Hitzdrahtinstrument, «Forschungsar-beiten auf d. Gebiete des Ingenieurwesens)?, 1933, 3; 12) Ziegler M., The Application of the Hot-Wire Anemometer for the Investigation of the Turbulence of an Airstream; «Versi, d. Kon. Akad. v. Wetenseh.», Amsterdam, v. 33 11930>, p. 723; 13) Ziegler M., A Complete Arangement for the Investigation, the Measurement and Recording of Rapid Air-Speed Fluctuations with very Thin and Short Hot Wires, v. 34 (1931), p. 663; ¹⁴) Dry-den H.a. Kuethe A., The Measurement of F uctuattons of Air-Speed by the Hot-Wire Anemometer, «T. Rep. NACA* 320; 15) Dry den H. a. К u e t b e A., Effect of Turbuhnce in Wind Tunnel Measur ment, ibid., 342; ιβ) Mock W. a. Dry den H., Improved Apparatus for the Measurement of Fluctuations of Air Speed in Turbulence Flow, ibid., 448. Б. Ушаков.

XII. Международная стандартная атмосфера [¹,²,³].

Необходимость унификации изменчивых атмосферных условий для возможности сравнения результатов испытаний летательных аппаратов с расчетами и сравнения различных аэродинамич. расчетов между собой привела к созданию т. н. международной стандартной атмосферы, в которой изменения по высоте давления, плотности и t° подчинены вполне определенным соотношениям, близким к средним действительным величинам. Для уровня моря приняты следующие начальные данные: г°=15°, темп-ра абсолютная Т°=288°, давление р₀=760 миллиметров Hg=10 332,276 килограмм/м², весовая плотность воздуха γ₀=1,2255 килограмм/м“, плотность воздуха ρ₀ =

= ^=0,1250 килограммск²/м⁴. Воздух считается сухим,

совершенным газом, для которого действительно уравнение Клапейрона. Газовая постоянная #=29,2708. До высоты ζ=11 000 м“ изменение 1° происходит по следующему закону:

t_z — а * z (1)

или

T_z=T₀ — а * z. (2)

Значение градиента а равно 0,0065 °С/м. Начиная с 11 000 метров и выше, t° считается постоянной и равной —56,5°. Из ур-ия Клапейрона следует,

что	р=ϋγΤ — RgqT
или	Pz _ Yz Те _ΰζ Tz Ρ0 У0 То Q0 То“		[Щ
откуда	^=ТОроГО-та=°’03416Тг*		(4
Если давление pz выражено в миллиметров Hg,		TO
	г г а т i Pz ММ Hg γζ — 0,4644 1 z		щ
Изменение	давления и плотности от	z=0	д»
2=11 000 метров происходит по ф-лам Бьеркнесса:
Pz _	ll “ zY5’256 — ίι — ζ	5 »256	(6)
Ро	ν To j ~ г 44 300	»
Уг _ Qz :	а «5б_ z	4 »256	(7)
У0 Q0	- V1 То I1 44 30oJ	1 >
из ф-лы (7) получаем
	_ То Γι _ /м0’2351
	z-vL1 Iro J
или	z=44 300 - 42 230 у/’235.		(8)

Приведение данных испытаний к условиям стандартной атмосферы делается след, обр.: по измеренным значениям p_z и T_z по формуле (4) или (5) определяют y_s, а из ф-лы (8) находят соответствующее значение высоты z в стандартной атмосфере. Приращение высоты Δζ при уменьшении давления на величину Ap=p_L—p₂ выражается следующим соотношением д _ _ 13,59Δρ миллиметров Hg /0*

² Уш * ^;

где у_т — среднее значение плотности между давлениями р, и р₂. От высоты 11 000 метров и выше закон изменения плотности и давления одинаков и соответствует формуле Галлея:

__ 3-11 000

_Pz_ _ Qz _ _с 6 340 _β (10)

Pz=11 000 Qz=11 000

Численные значения международной стандартной атмосферы через 1 000 метров от z=—1 000 метров до z=15 000 метров приведены в таблице 19.

* Для стандартной атмосферы, принятой в США„ эта высота равна 10 769 метров В соответствии с этим предельная f равна не — 56,5° а — 55° (смотрите нише).

Таблица 19. — Международная стандартная атмосфера.

η N	р m	О m N Еч	о Е-ч Ь-ч“	о а Λ	о а» ’ν О	Р В миллиметров Hg	n| С» Οι	со < > £
-1 000	21,5	294,5	1,023	1,124	1,100	854,6	0,137	1,348
0	15,0	288,0	1,000	1,000	1,000	760,0	0,125	1,226
1 000	8,5	281,5	0.978	0,887	0,907	674,1	0,113	1,112
2 000	2,0	275,0	0,955	0,7s5	0,822	596,2	0,103	1,007
ЗОЮ	- 4,5	268,5	0,932	0,692	0,742	525,8	0,093	0,909
4 000	-11,0	262,0	0,910	0,60^	0,669	462,3	0,084	0,819
5 000	-17,5	255,5	0,887	0,533	0,601	405,1	0,075	0,736
6 000	-24,0	249,0	0,865	0,466	0,538	353,8	0,067	0,660
7 ООО	—30,5	242,5	0,842	0,405	0,481	307,9	0,060	0,590
8 000	—37,0	236,0	0,820	0,451	0,429	266,9	0,054	0,525
9 000	—43,5	229,5	0,797	0,303	0,381	230,5	0,048	0,466
10 000	-50,0	223,0	0,774	0,261	0,337	198,2	0,042	0,413
11 000	-56,5	216,5	0,752	0,223	0,297	169,4	0,037	0,364
12 000	-56,5	216,5	0,752	0,190	0,253	144,6	0,032	0,310
13 000	-56,5	216,5	0,752	0,163	0,217	123,7	0,027	0,265(
14 000	—56,5	216,5	0,752	0,139	0,135	105,6	0,027	0,227
15 000	-56,5	216,5	0,752	0,119	0,158	90,1	0,020	0,194
ζ—высота в м; tz— темп-pa на высоте z в РС; Tz — абс. темп-pa на высоте : в °С; Х0 —абс. темп-pa на земле (0 м); ρζ—давление воздуха на высоте г; Ро— давление воздуха на земле (0 м); qz—массовая плотность воздуха на высоте ζ; со — массовая плотность воздуха на высоте 0 м; γ—весовая плотность воздуха.

Лит.: Чев А., Международная стандартная атмосфера и приведение к ней результатов полетных испытаний самолетов, «Труды ЦАГИ», вып. 42, стр. 161— 179; Сборн. «Самолетостроение», М., 1931, стр. 53—57; Diehl W., Engineering Aerodynamics, р. 267—273, Ν. Y., 1928; Technical Report of the National Advisory Committee for Aeronautics, 218; Standard Atmosphere Tables and Data, Wsh., 1925. Б. Ушаков.