> Техника, страница 17 > Аэродинамина

Аэродинамина

Аэродинамина, наука, изучающая движение газообразных жидкостей (здесь газ рассматривается как идеальная жидкость) и реакции, которые получаются на помещенные в них твердые тела. А.—часть гидродинамики (смотрите). Принципиальная разница между А. и собственно гидродинамикой заключается в том, что газообразная жидкость, с которой оперирует А., является жидкостью сжимаемой, тогда как в гидродинамике рассматривается жидкость капельная, несжимаемая. Однако и в А. во многих случаях принимают газообразную среду (воздух) также несжимаемою. Свое техническое приложение А. получает гл. обр. в авиации, где она касается изучения обтекания твердых тел определенных форм и нахождения сил, действующих на эти тела. Как и в гидродинамике, А. рассматривает главн. образом совершенную, идеальную газообразную жидкость, без вязкости, ибо интегрирование ур-ий движения вязкой жидкости настолько сложно, что м. б. выполнено лишь в немногих частных случаях. Для случая несжимаемой вязкой жидкости задача частично решена только для обтекания шара (задача Стокса) и эллипсоида; поэтому в А. в большинстве случаев приходится отказаться от рассмотрения того сопротивления тел, движущихся в жидкости, которое зависит от трения, а рассматривать лишь сопротивление, зависящее от.

Фигура 2.

возмущения телом набегающего на него потока жидкости. А. идеальной жидкости рассматривает только силы, получающиеся перпендикулярно направлению движения, т. н. подъемные силы, и лишь в самое последнее время в А. стала развиваться самостоятельная часть, т. н. теория индуктивного сопротивления, которая учитывает также вызываемое сбегающими с тела вихрями лобовое сопротивление, то есть сопротивление, направленное по движению потока. Вследствие идеализирования жидкости теоретическая А. не может дать для практики полного ответа о возникающем сопротивлении жидкости движущемуся в ней телу; поэтому приходится пользоваться опытными данными и с помощью соответствующих коэффициентов исправлять и дополнять те выводы о величине сопротивления, которые дает .теория. А. состоит из двух частей: теоретической“ опирающейся на общие законы классической механики, и прикладной, или экспериментальной, оперирующей с опытными данными, дополняющими общие выводы теоретической аэродинамики.

I. Аэродинамика теоретическая.

Общие уравнения движения жидкости форме Эйлера будут следующие:

1	dp	_ v	ди	ди	du	du
ρ	дх	- л. —	U дх	VJ~y~	Ί0 "г dz	~W
1	dp	_ V	dv	dv	dv	dv
ρ	д,у ~	= I —	“i - дх	V~dy~	Ί0 -t-- dz	~dt’
1	др	_ у	dw	div	dw	dw
ρ	dz	- /j —	“ дх	V dy	ΊΟ dz	~dt’

в

όρ, 0(ρΐή, 0(ρν), _Λ

dt ⁺ ~dx~ ^{+ + =} ’

где X, Y, Z—силы, действующие на массу, и, V, w—компоненты скорости по осям координат, а р и ρ—давление и плотность. Последнее ур-ие выражает собой условие непрерывности упругой жидкости. Здесь надо находить 5 неизвестных: р, ρ, и, v, w как функции х, у, ζ и t—поэтому этих ур-ий недостаточно. Для установления связи между ρ и р рассматривают процесс изменения состояния воздуха адиабатическим или по-литропичееким. Зависимость между р и ρ можно выразить след, ббразом: р=£. ργ, где у— коэфф., выражающий отношение удельных тепл от газообразной жидкости, в случае адиабатического процесса для воздуха равный 1,408; ξ—кбэфф., характеризующий степень сжимаемости. Продифференцировав это ур-ие, найдем, άρ=ξγρ^Ί1άρ

V

или (1р=у ~ (Ιρ. Т.к.скорость звука в данной среде выражается ф-лой с=л _γ ^р, то имеем у ρ

dp

^с“=-_d-, т. e. изменение плотности в зависимости от давления пропорционально квадрату скорости звука в данной среде. Вследствие того, что скорость звука в воздухе только в четыре раза меньше, чем в воде, во многих вопросах или задачах А. можно принимать воздух несжимаемым и лишь при больших скоростях движения, приближающихся к скорости звука, приходится принимать во внимание сжимаемость воздуха. Уравнение непрерывности в этом случае примет вид: ди ,dv dw_ дх dydz~

Установившимся движением жидкости называется такое движение, когда в любой точке в потоке скорость не зависит от времени. Уравнения движения в этом случае для несжимаемой жидкости примут вид:

1	др	_ Ύ	ди	— V	du	- w	du
ρ	дх	— А-	11 дх		ду~		~dz’
1	д р __		dv	— V	dv	-w	dv
ρ	ду	= 1 —	Н дх		ду		dz’
1	др	— 7	dw Лй___.	— V	dw	- w	dw
ρ	dz ’	— л —·	дх		Ту~		dz’
		ди	dv	dw	= 0.
		дх	ау +	dz

Обозначим через V полную скорость частиц, т. e. V — Vu² + v² + го². Подставляя это выражение в ур-ие движения и производя соответствующие преобразования, получим: 1 dp d(F²) _0/„„. ρ дх дх ^Ζ ^ ’

X —

1

ρ ду д^у

i а_?_ф ₌

ρ dz dz ^{v J}

ди dv дго _ _n

_ tm 1 Idw dv

где введены обозначения: ξ=— ^ζ

2

ди диЛ _ 1 /dv ди

dz дх) ’ * ^— 2 ()а? ду

Эти вы ражения называются компонентами вихри и представляют собою проекцию на оси координат угловой скорости вращения частиц жидкости. Положим, что жидкость не завихрена, тогда £=»?=ζ=0; а отсюда dw ον ди dw dv ди _

dj^!=rz^;0z ⁼ di^;di⁼di· ^{Этиурия п}°-

называют, что должна существовать нек-рая

dw

функция φ, обладающая свойством: ^=п ;

дф дф,

—=v; -^z=w. Функция φ называется функцией потенциала скоростей и аналогична потенциальной (силовой) функции в механике. Т. о. в установившемся невихревом потоке должна существовать функция потенциала скоростей. Семейство поверхностей ф(х, у, ζ) — φ называется эквипотенциальными поверхностями, причем скорости частиц жидкости нормальны к эквипотенциальным поверхностям. Решить задачу о движении потока в трех измерениях представляет значительные трудности, поэтому приходится прибегать к упрощающим схемам, как двухразмерный поток или плоскопараллельный поток. Разработанная до сих пор теория крыльев — теория несущих поверхностей— оперирует гл. обр. с плоскопараллельным потоком, причем задачи этой теории могут с некоторыми поправками быть перенесены и для случая трехразмерного потока, обтекающего аэроплан-ное крыло. До некоторой степени эти поправки вводит теория индуктивного сопротивления. Плоскопараллельным потоком называется поток, текущий между двумя параллельными плоскостями; скорости в нем имеют одну и ту же величину и направление во всех точках, лежащих на одной нормали к этим плоскостям. Семейство линий тока, то есть линии, которые описывают частицы жидкости при своем движении, м. б. выражено в виде ур-ия гр(х, у)=хр, где ip называется функцией тока; скорость, нормальная к направлению s, будет выражаться ф-лой dip

q_п=0-, а компоненты скорости по двум взаимно перпендикулярным направлениям вы-разятся так: ?=+—; v=— Т. о. быстрота изменений функции тока характеризует собою скорость потока. Для случая плоскопараллельного потока общие уравнения движения для несжимаемой жидкости примут вид:

1 dp _ du du du

ρ dx ^U dx ^V dy dt’

1 dp „ dv dv dv

q dy dx dy dt

du dv dx ^ by ~

Интегрирование даже этих уравнений плоскопараллельного потока представляет большие трудности, поэтому для решения многих вопросов А. прибегают к искусственным методам; одним из таких методов является применение теории источников.

Источником называется точка в пространственном потоке, из которой в единицу времени вытекает одинаковый объём жидкости (иногда рассматривается источник с переменным расходом, то есть пульсирующий источник). Отрицательным источником, Фигура i. Схема линей- или стоком, называет-ного источника. ся точка в пространстве, через к-рую жидкость уходит из потока. Силой, или напряжением, источника называется объём жидкости, выходящей в единицу времени из источника. В случае плоскопараллелыюго потока источники и стоки называются линейными, ибо жидкость в линейном источнике приходит или уходит из потока через линию, нормальную к потоку. В случае наличия линейного источника в первоначально покоящейся жидкости, из источника жидкость будет выходить по радиальным направлениям; если т—сила источника, то радиальная скорость на радиусе г выразится

УУ1

ф-лой: и=2^· Линии тока в этом случае будут радиусами (фигура 1), исходящими из

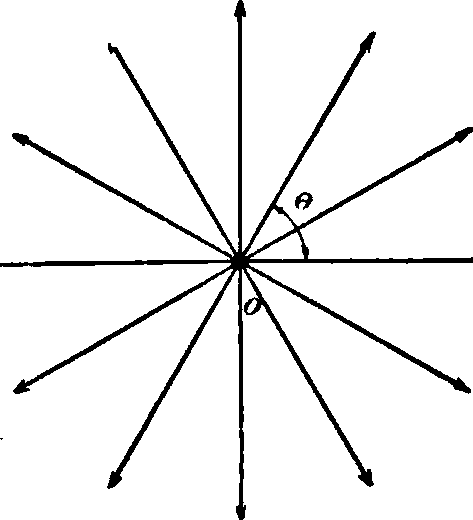
источника, а функция тока хр выразится т _

так: ip=Θ.

Если рассматривать источник в потоке, движущемся равномерно со скоростью F, параллельной оси X, то функция тока в этом

ш

случае будет иметь вид: ip=— V-у + — Θ.

671

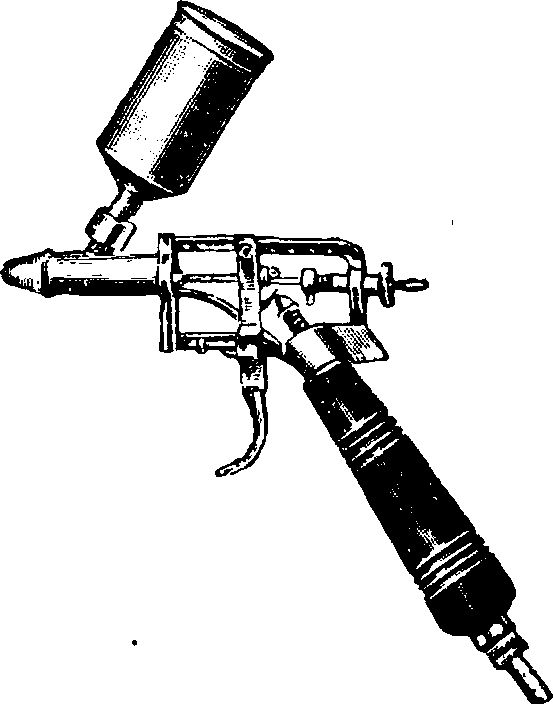
При одновременном действии источника и стока с равными силами (фигура 2) функция

ТУЬ 7YI

тока принимает вид: (Θi — Θ₂)=φ,

67Ζ 67Ζ

где <9₂ и φ — углы, указанные на чертеже. Полагая начало кординат проходя-

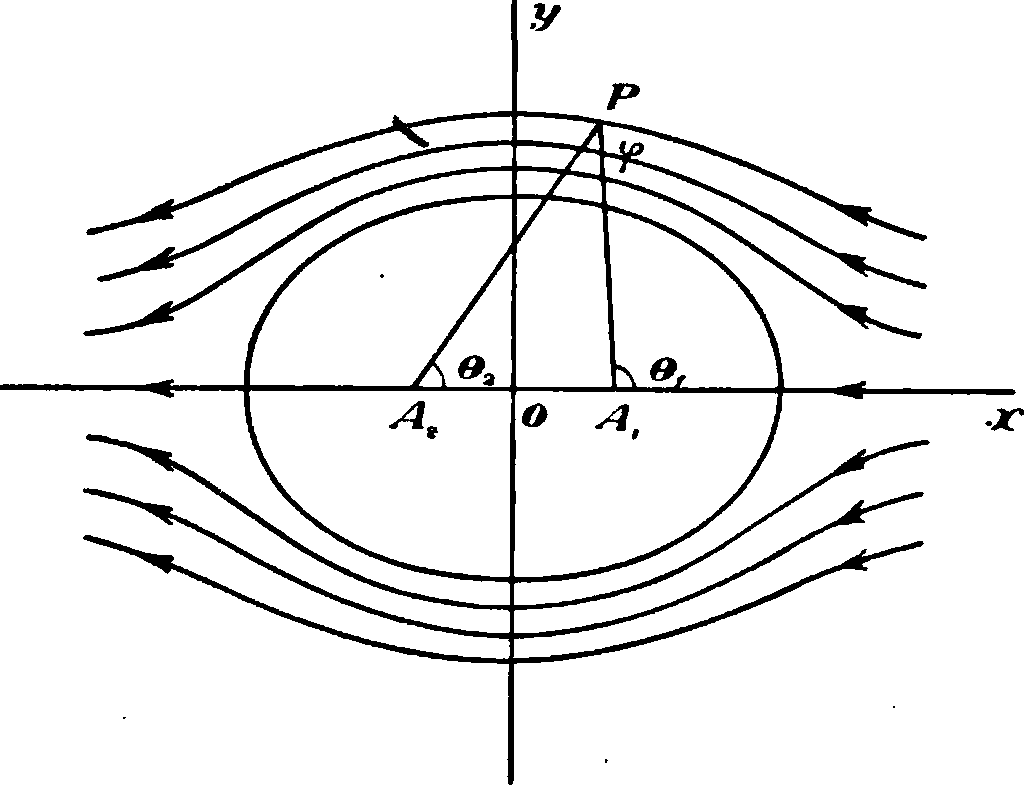
Фигура 2. Схема источника и стока. щим через точку, находящуюся на середине между источником и стоком, и обозначая расстояние между ними через 2s, получим выражение для функции тока в таком виде: m. 2 ys _

ip=arc tg „—Если теперь при-

2тс х“-{-у²—s²

ложить к нашим потокам равномерный поток, текущий параллельно оси×со скоростью V, то функция тока такого сложного потока будет иметь вид:

„, ш _х 2 ys

ip =— V.y + arc tg --г

^{Ύ ϋ} 2π χ² + у¹ — s²

Полученная функция тока может быть приложена для изучения обтекания потоком тел, имеющих в сечении продолговатую форму. Изменяя силы источников и принимая очертание замкнутой линии тока, проходящей через критические точки, то есть точки с нулевой скоростью, за очертание сечения твердого тела, к-рое похоже на очертание сечений тел, применяемых в авиации, можно этим методом изучить те давления, которые получаются в этих формах. В случае пространственного потока методом источников изучают давление на дирижабли. Положим теперь, что источник и сток приближаются друг к другу, причем произведение силы источника на расстояние между источником и стоком имеет постоянное значение μ — 2ms. Такие совмещенные источники и стоки носят название дублетов; функция тока в случае дублета примет вид: гр=~;=J·sin Θ. Прибавим к

2л х² + у^г 2л ^с

рассматриваемому потоку равномерный поток, текущий II оси×со скоростью V;

функция тока будет иметь вид: ψ=—V.y + Линия тока гр=0 будет со-

+

μ

у

μ

2 я X^я + у¹

стоять из оси×и из круга х^я + yⁱ — ^ ^у

Т. о., принимая очертания линии тока ψ=0 за сечение твердого тела, мы получаем обтекание этого тела потоком, движущимся со скоростью V. Источники и стоки, а также и дублет обладают свойством независимости действия, то есть к действию источников можно прикладывать любые потоки, причем сложение скоростей делается геометрически, а потенциалов—алгебраически.

Для решения многих задач А. бывает удобно применять теорию функций комплексного переменного, которая дает возможность сравнительно просто строить потоки несжимаемой жидкости. Это применение основано на том свойстве функции тока и функции потенциала скоростей, д<р dip όφ _ dip

ЧТО -Z-=~,

dx dy dy

dx’

этим же свой ством обладает функция комплексного переменного вида: f(z) — <р + W- Функции ψ и ip обладают еще тем свойством, что кривые, семейство которых они собою выражают, взаимно ортогональны. Рассмотрим функцию f(z) комплексного переменного ζ=х + гу, однозначную и конечную на всей плоскости. Пусть ξ и η — действительная и мнимая части этой функции: f(z)=ζ=ξ+гη. Кривые постоянных значений ξ и η м. б. представлены на плоскости z как семейство взаимно ортогональных линий, соответствующих потенциальной функции и функции тока. С другой стороны, ξ И η можно рассматривать как абсциссу и ординату новой системы координат, в которой ζ есть комплексное переменное. Каждая кривая на плоскости е м. б. перенесена на новую плоскость ζ. Т. о. семейство кривых линий плоскости z трансформируется в семейство взаимно ортогональных прямых плоскости ζ. Так, например, бесконечно малый треугольник на плоскости г· преобразуется помощью указанного способа в бесконечно малый треугольник на плоскости ζ, с сохранением величины углов. Преобразование описанного вида называется конформным преобразованием, и в А., гл. обр. в теории крыльев, это преобразование получило большое применение, т. к., поставив условие, что функции потенциала скоростей и расходы потока при этом преобразовании не меняют своей величины, получаем возможность, зная потоки в одной плоскости, находить соответственные им потоки в другой; при этом линии тока и эквипотенциальные линии в одной плоскости конформно преобразуются в таковые же линии в другой плоскости, расходы же и разности потенциалов скоростей на соответствующих друг другу конформно отрезках кривых остаются неизменными. Кроме того, можно доказать, что при конформных преобразованиях потоков циркуляция (смотрите Вихревая теория) не меняет своей величины. Так. обр., если найден поток обтекания тела какой-либо формы, то помощью кон формного преобразования можно найти другой соответствующий этому преобразованию поток и, следовательно, поток, соответствующий обтеканию другого тела. Вся трудность в такого рода построении потоков заключается в подборе подходящей функции преобразования.—В теории крыльев обычно исходят от потока, обтекающего цилиндр, ибо выражение этого потока можно - легко найти, пользуясь потоком, ео-Фигура 3. Обтекание цилиндра, здаваемым дублетом. Мы выше уже получили выражение для функции тока дублета; принимая очертание линии тока ψ=0 за сечение цилиндра, помещенного в потоке, получим:

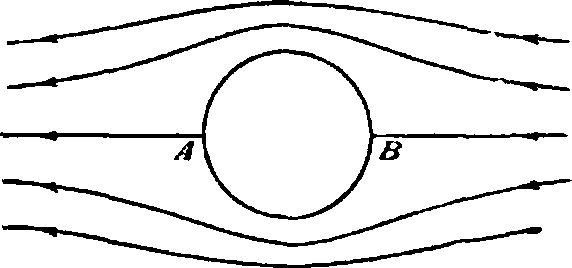
xp=—V.y 1 — --= =

а²

—V [г — ~ sin Θ,

где а—радиус цилиндра (фигура 3). Радиальная и тангенциальная скорости в любой точке потока будут:

и =

1 dip г άθ

ν =

dip

dr

F|1 -ficose, Г|1+£]от

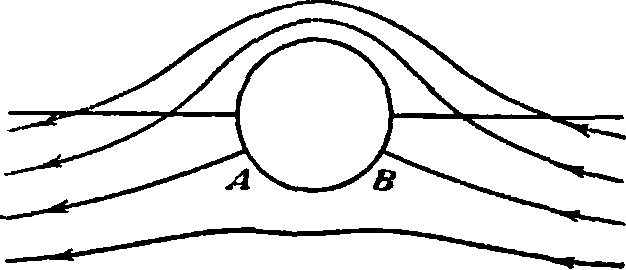
Как видим, на поверхности цилиндра радиальная скорость равна нулю; кроме того, величины скоростей симметричны относительно осей координат. Т. о., в силу того, что количества движения при таком обтекании не создается, тело не испытывает никакого сопротивления движущемуся потоку. Этот вывод в обобщенном виде носит название парадокса Эйлера. В точках А я В цилиндра имеются две критические точки, в которых и тангенциальная скорость равна нулю. Для целей практики более интересным случаем обтекания цилиндра является несколько иной случай.

Рассмотрим так называемым циркуляционный поток (фигура 4), то есть поток, в котором частицы жидкости двигаются по концентрическим окружностям. Такой поток м. б. вызван прямолинейным вихрем (ем. Вихревая тео- φ_ΙΙΓι 4 схема циркуля-рия) С ЦИркуЛЯЦИ- ционного потока, ей J. Пусть начало координат находится в центре вихря; радиальная составляющая скорости будет равна нулю, а скорость по окружности ν выразится так: ν= ^—Отсюда получаем выражение для функции тока у>= — lg г.

2 л

Сложим теперь согласно принципу независимости два потока, обтекающих цилиндр:

один с функцией тока ψ=—V.y ^ 1 — ^ j, а

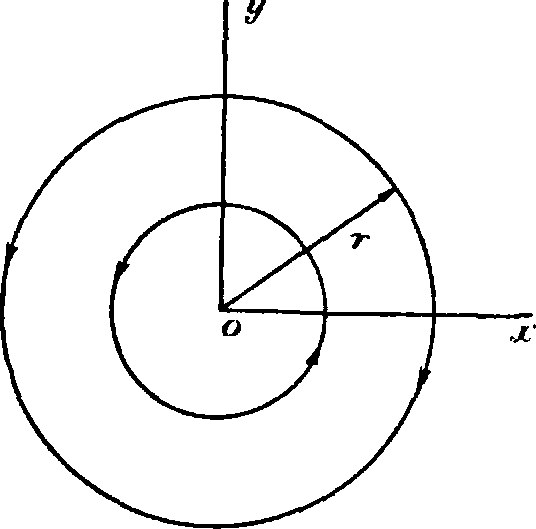
Т. 9. m. I.

27

другой, циркуляционный ψ=— ~ lg г; ииы-

Z п ми словами, мы заменяем наш цилиндр дублетом и прямолинейным вихрем, проходящим через ось цилиндра (фигура 5). В полученном сложном потоке функция тока будет иметь вид:

V—Igr.

Радиальная и тангенциальная скорости выразятся уравнениями:

и

1 dw г д&

= — F 1

а“

μ

dr

(1‘

cos Θ, J

1 + -_T sin Θ + -

r“ j 2 nr

На поверхности цилиндра будем иметь:

J

и— 0 и r=2Fsin

2 па

Фигура о. Обтекание цилиндра с циркуляцией.

Критические точки А и В,то есть точки нулевой скорости на поверхности цилиндра, найдем, полагая ν=0, т. e. sin Θ=—~~rr ·

4 παν

В данном случае образуется нек-рое количество движения, и поэтому появляется и нек-рая сила сопротивления. Эта сила получается за счет разности давлений с одной и другой стороны цилиндра, причем эта разность давлений, в свою очередь, получается вследствие различных скоростей в этих местах. Зависимость между давлением и скоростью дается по уравнению Бернулли (смотрите Гидродинамика):

QV^

р -г -2~=Const. На одной стороне цилиндра имеется пониженное давление и повышенная скорость, а на другой—повышенное давление и пониженная скорость. Подставим в ур-ие Бернулли значение скорости на поверхности цилиндра:

р + (2V sin Θ + —)=Const.

2 2 па]

Полное давление на цилиндр длиной d~ будет:

/2^

р sin Θ.α άθ. о

Подставляем сюда выражение для давления па цилиндре:

dP=dz J j Const —

— (2rsin Θ -j- l” si

2 2 na] J

sin Θ.α d&.

Проинтегрировав это выражение, получим: dP=ρ JVdz, τ. е. сила реакции жидкости на цилиндр с циркуляцией J перпендикулярна направлению скорости в бесконечности, равна плотности жидкости, помноженной на циркуляцию, на скорость потока в бесконечности и на длину цилиндра dz. Направление этой реакции получается, если взять вектор, представляющий скорость в бесконечности, и повернуть его на прямой угол в сторону, обратную циркуляции. Это — теорема Жуковского, на которой основывается вся теория крыльев. Здесь дан вывод ее только для цилиндра, Жуковским же она обобщена и потому приложима и определению подъемной силы любых тел, движущихся в потоке. Т. о. сила сопротивления тела, движущегося в идеальной жидкости, получается лишь при наличии циркуляции, причем эта сила сопротивления является подъемной силой, то есть силой, перпендикулярной к скорости движения. Сила лобового сопротивления до последнего времени совсем не учитывалась, и лишь с возникновением теории индуктивного сопротивления этот парадоксальный вывод А. идеальной жидкости был до известной степени восполнен. Зная обтекание цилиндра, то есть имея для него выражение функции тока и подъемной силы, можно найти и обтекание других тел, делая конформные преобразования потока, обтекающего цилиндр. Наиболее интересными преобразованиями являются преобразования, предложенные проф. С. А. Чаплыгиным («О давлении плоскопараллельного потока на преграждающие тела»). Некоторые из них подверглись детальному изучению за границей и носят название преобразований Жуковского. Преобразования Жуковского лишь по методу отличны от преобразований Чаплыгина, хотя оба приходят к одному и тому же результату. Функция этих

_ „ I ( а“

преобразовании имеет вид: ζ=Н £ + —

С помощью этой функции можно преобразовать круг в различные виды кривых, к-рые, являясь инверсиями кривых второго порядка, по своему очертанию очень хорошо подходят к профилям крыльев аэроплана. Трефцем (Trefftz) предложен очень простой геометрический метод построения этих профилей, основанный на геометрических свойствах конформных преобразований. Пусть мы имеем круг и внутри его другой соприкасающийся (фигура 6); проведем из точки соприкосновения под углом φ к прямой, с оединяющей эту точку с центрами кругов, прямую; из точки 0 на этой прямой проведем два луча под одинаковыми углами & к прямой; соединяя точки пере-_ „ „ сечения этих л V-

Фигура 6. Построение инверсии „ _τ,„_τττ,₀»ΐττ

параболы по методу Трефца. ^с кругами прямыми линиями с противоположными точками пересечения и деля эти отрезки прямых по-t полам, получим искомую точку на кривой профиля. Изменяя угол д от 0 до π, получим весь профиль. При угле наклона прямой φ равном нулю получается симметричный профиль. Такого рода профиля суть инверсии параболы и за границей носят название профилей Жуковского.

	—/« р i X X х Д i» —“нГ
f
°	/θ /: 7 < : i
	*
	— Р

Если немного раздвинуть два круга так, чтобы один оставался в другом, и произвести такие же построения, получим профиля, предложенные Чаплыгиным,—инверсии эллипса. У инверсий эллипса, в отличие от инверсий параболы, не будет заостренного заднего кончика. — Мы рассматривали крыло только в плоскопараллельном потоке, то есть отрезок крыла, равный ширине потока; в трехразмерном потоке это будет соответствовать крылу бесконечно большого размаха; на практике же приходится иметь дело с конечным размахом. Разница в обтекании крыльев бесконечно большого и конечного размаха заключается гл. обр. в том, что в последнем на концах образуются сбегающие вихревые жгуты, на образование которых тратится некоторая энергия; кроме того, эти вихри изменяют поле около крыла. В теории индуктивного сопротивления (смотрите) рассматриваются эти потери, а также и те поправки, которые необходимо сделать, прилагая к крылу конечного размаха выкладки теории крыла в плоскопараллелыюм потоке.

II. Аэродинамика экспериментальная.

А. экспериментальная базируется гл. обр. на основном законе сопротивления, к-рый дает зависимость сопротивления тел, движущихся в жидкости, от плотности и вязкости среды, в которой движется тело, размеров, скорости движения и формы его. Общее выражение этого закона можно дать в виде следующей ф-лы:

В — qPv²F (ρ,Ι,ν,ν), (1)

где В—сопротивление тела, ρ— плотность жидкости, I — линейный размер тела, ν — скорость движения тела и F—функция указанных величин и вязкости жидкости ν. Посмотрим, как выражается вязкость ν. Пусть ds— элемент площади в жидкости и п — нормаль к этой площади; в точке ленд кости, находящейся на расстоянии dn по нормали от элемента ds, скорость будет ν + dn. Согласно гипотезе Навье-

Стокса, тангенциальная сила на рассматриваемый элемент выразится:

₇ до,

pds=μ _д— ds. (2)

Коэфф. μ называется коэфф-том вязкости. Чаще рассматривают другой коэффициент

ν=—, где ρ— плотность лбидкости. Коэфф. ν Q

называется кинематическим коэфф-том вязкости. Его размерность найдется из ф-лы (2) и будет [кг°мЧк~^г]. В общей формуле сопротивления размерность ρΡν²· есть размерность силы, следовательно F (ρ,Ι,ν,ν) должна иметь размерность нуль, а это получается при одной только комбинации величин

ρ,Ι,νιιν, именно, полагая Β(ρ,Ι, ν,ν)=F

Таким образом имеем:

д=(3)

Следовательно, два течения можно считать подобными только в том случае, если ве-

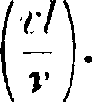
0-2

см

1-0

2-0

3-0

40

Фигура 7. Зависимость коэфф. сопротивления от скорости.

vl „

личина — остается одной и той же. Это есть

V

выражение закона аэродинамич. подобия;-^- называется числом Рейнольдса. Ф-ла (3) обычно пишется в следующем виде: В=CoSv (4)

где S — миделевое сечение тела (наибольшая площадь сечения тела, перпендикулярного направлению движения) или какое-нибудь другое измерение площади, характеризующее величину тела, и С — нек-рый коэфф., зависящий от формы тела. Если считать С независящим от скорости, то, как показывает ОПЫТ с и как явствует °^3г из выражения (3), не на всем диапазоне скоростей будет справедливо выражение (4): на малых скоростях (до 1 м/ск) оправдываете я закон первой степени скорости; при больших скоростях, близких к скорости звука, повидимому, имеет место закон кубов; при скоростях же выше звуковой опять наблюдается закон квадратов. Принимая всюду закон квадратов, следует ставить коэффициент С в зависимость от скорости. На фигуре 7 представлена зависимость этого коэфф-та от отношения скорости движения тела к скорости звука. Однако на том диапазоне скоростей, при к-ром приходится иметь дело с аэроплан-ными деталями (от 20 до 80 м/ск), закон квадратов скоростей довольно хорошо оправдывается. Вообще говоря, законы сопротивления тел при скоростях выше 100 м/ск пока еще недостаточно хорошо изучены. Сверхзвуковые скорости имеют место в артилл. снарядах, и поэтому изучение сопротивления при таких скоростях относится к области внешней баллистики (смотрите Баллистика). Коэфф. С в формуле сопротивления (4), как видно из выражения (3), является безразмерным, поэтому этот коэфф. называется абсолютным коэфф-том. Иногда формулу сопротивления пишут: В=KSv², то есть К=Ορ, так что К зависит от плотности среды. В Германии сопротивление относят не просто к скорости, а к скоростному напору, то есть пишут: В= CqS, где 2= % ρν^г. Т. о. зависимость между различными коэфф. выразится так:

Г=К-=^С-.

ρ 2

Мы уже видели, что в идеальной жидкости тела не испытывают лобового сопротивления. На самом деле полного обтекания потоком тел не бывает, а за телом образуется б. илим. интенсивное завихрение, к-рое вместе с трением и создает наблюдаемое сопротивление. Это вихреобразование зависит от места возникновения срыва струи от поверхности тела и поэтому зависит от формы тела; этим и объясняется зависимость коэффициента С от формы тела. Одним из наиболее неустойчивых по вихреобразова-нию тел является шар. Исследования вих-реобразования производятся получением т. н. аэродинамич. спектров, то есть фиксированием каким-либо образом линий токов в данном течении (смотрите ниже). На фигуре 8

Фигура 8. Обтекание плоской пластинки на малой скорости. дано обтекание плоской пластинки, поставленной перпендикулярно потоку, при малых скоростях; в этом случае вихреобра-зования не наблюдается, и поток почти симметричен; лобовое сопротивление в данном случае создает почти одно только трение. На фигуре 9 — обтекание той же пластинки при бблыпих скоростях, когда начинают появляться вихри. Сопротивление плоской квадратной пластинки, поставленной нормально к потоку, в экспериментальной А. иногда служит эталоном для сравнивания сопротивления различных тел. Сопротивление данного тела приводят к сопротивлению т. н. эквивалентной пластинки по ф-ле: B-Cqov“, где В—сопротивление данного тела, С—коэфф. сопротивления плоской пластинки, принимаемый равным 0,64, и а —

Фигура 9. Обтекание плоской пластинки на большой скорости. площадь пластинки. По этой формуле находится площадь эквивалентной пластинки В

и=- g₄~_ra ’ которой и характеризуется сопротивление данного тела. В таблице даны коэффициенты лобового сопротивления С для некоторых форм:

Плоская квадратная пластинка, поставленная нормально к направлению по тока 0,64

Круглый плоский диск, поставленный нормально к направлению потока.. .. 0,6 6

Шар0,25

Эллипсоид с большой осью, направленной перпендикулярно потоку..0,30

То же, но с большой осью по потоку. 0,035 Веретенообразные тела с передним тупым. а задним заостренным концом (тело наитучшего обтекания), при отношении длины к диам. 4 (ось но току).. 0,013

Цилиндрические тела, имеющие в сечении форму тела наилучшего обтекания (стойки аэроплана) с осью 1 к потоку. 0,045 Цилиндрические тела, имеющие в сечении круг (круглые трубы, проволока).о,60

Профилированная проволока — в зависимости от отношения размеров сечения. .0,15—0,2 0 Фюзеляжи — в зависимости от формы. 0,3 5—0,50 В приложениях А. наибольший интерес представляют тела малого сопротивления, а такими будут тела, при движении которых вихреобразование получается наименьшим. Как показывает опыт, наименьшее вихреобразование получается для форм вытянутого вида, с утолщенным передним концом и заостренным задним. Подобные формы теперь обычно^придаются дирижаблям и по возможности всем деталям аэропланов, находящимся в потоке воздуха. В теоретической аэродинамике мы видели, что если вокруг тела получается циркуляция, то есть получается некоторая разность скоростей с одной и с другой стороны тела, то возникает также сила, перпендикулярная направлению движения. В виду того, что в авиации эта последняя сила играет большую роль, рассмотрим формы тел, которые дают эту силу сравнительно большой.

Рассмотрим тело крылообразной формы, то есть цилиндрическое тело, имеющее в сечении, перпендикулярном образующим, одну свою размерность меньшей, чем другую; положим, что сечение этого крыла имеет форму, представленную на фигуре 10. Это сечение называется профилем кр ы-л а, или дужкой крыла. Край этого профиля, на который набегает поток, называется передним краем профиля, или дужки, а с которого сбегает поток—з а д-ним краем. Угол между хордой нижнего очертания сечения и направлением потока называется углом атаки к р ы-л а. Хорда сечения крыла является линией условной. Обычно в профилях, имеющих одну сторону вогнутой или плоской, за эту условную линию принимается направление прямолинейной рейки, которая, будучи приложена к этой стороне, прикасается к очертанию профиля не менее как в двух точках. В профилях, имеющих выпуклые очертания с обеих сторон, такого положения рейки найти нельзя, и поэтому в этих случаях фиксируют какую-либо ли-

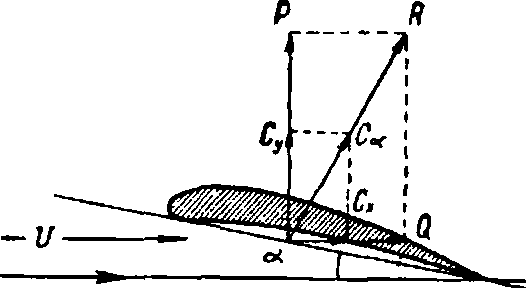
Фигура 10. Схема разложения силы действия на крыло. нию, принимая ее за хорду, и от нее делают отсчет углов атаки. Для симметричных профилей за хорду принимают продольную линию симметрии. Если крыло имеет нецилиндрическую форму и его хорды непараллельны друг другу, то углы атаки в разных сечениях будут разные. Из нецилиндрических крыльев наиболее употребительными являются формы, составленные из двух конических поверхностей; однако употребляются также и другие, более сложные крылья (смотрите Аэроплан). Полная сила сопротивления будет результирующей сил — подъемной и лобовой. С изменением угла атаки полная сила сопротивления меняет как свою величину, так наклон и место приложения на профиле. Для удобства исследования обыкновенно рассматривают на крыле не самую силу, а соответствующий коэффициент сопротивления, который ей пропорционален. Таким образом имеем:

R=CaQSv2,	(5)
P=CyQSv	(6)
Q-C1S“,	(?)

где С а называется коэфф-том полной силы, С_у—коэфф-том подъемной силы, С_х—коэфф. лобового сопротивления и S — площадь крыльев, то есть в случае цилиндрических крыльев—площадь, получаемая умножением ширины крыла (то есть длины отрезка хорды, отсекаемого перпендикулярами к хорде, касающимися передней и задней кромок крыла) на размах (то есть длину между крайними точками крыла, измеряемую параллельно образующим). Рассмотрим изменение величины этих коэффициентов в зависимости от угла атаки. — Подъемная сила с увеличением угла атаки увеличивается до некоторого максимального значения, а потом снова начинает падать; угол, соответствующий максимальной подъемной силе, называется критическим углом; величина его для различных профилей разная (примерно около 15—20°). На фигуре 11

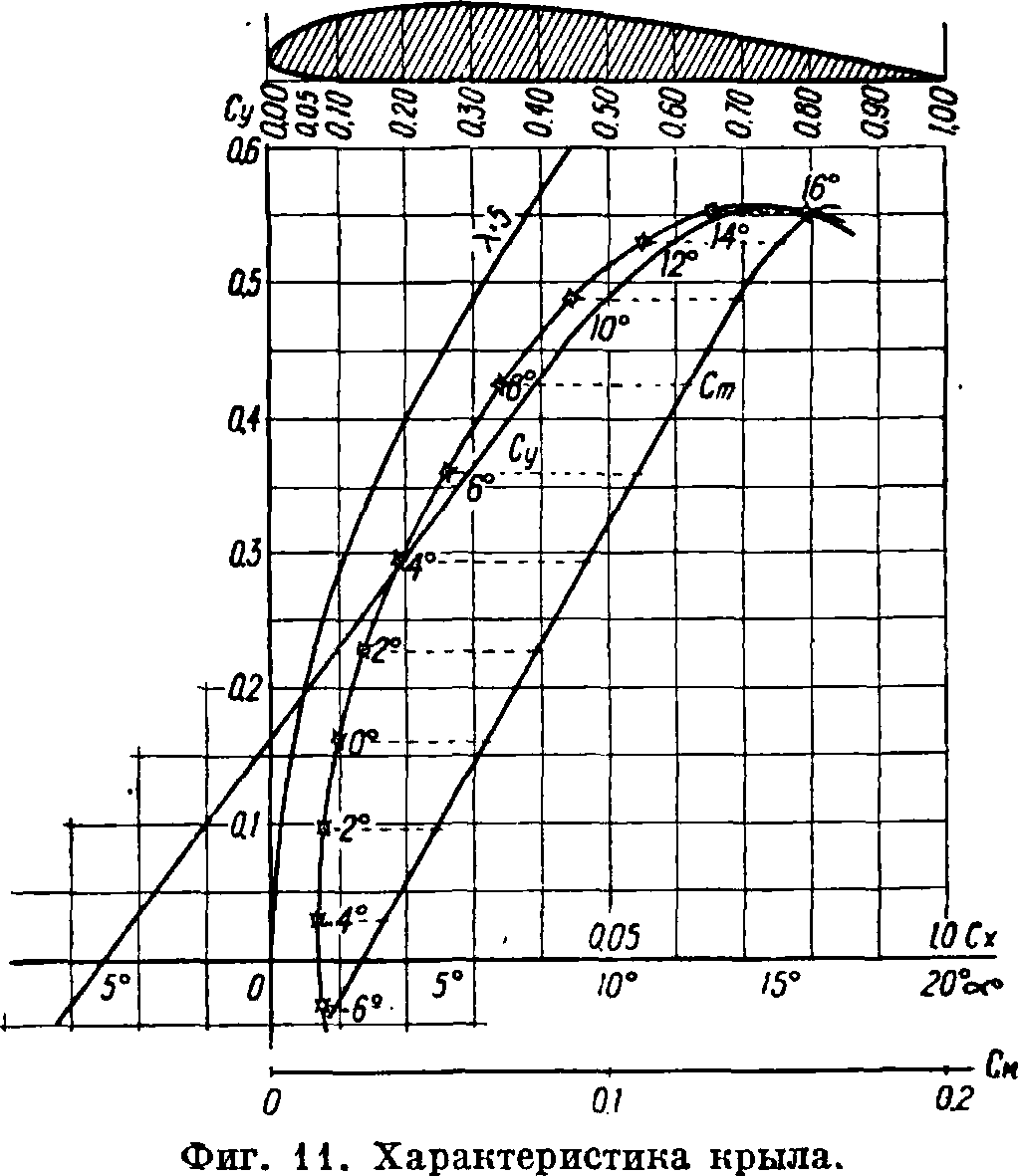
представлена указанная зависимость; как видим, закон изменения C_v, почти точно прямолинейный до критического угла, при больших углах атаки нарушается, вследствие появления срыва струй—При угле атаки 0° для несимметрич. профиля имеется некоторая подъемная сила. Линия, фиксированная на профиле и параллельная движению потока при нуле подъемной силы, иногда называется нулевой линией. Для симметричный, же профилей подъемная сила при угле атаки 0° равна нулю. Для авиации обычно бывает интересен лишь небольшой диапазон т. н. летных углов, примерно от —10° до +20°, поэтому и эксперименты делаются обычно в этих пределах и только для каких-либо специальных целей находят зависимость подъемной силы или полной силы от углов атаки в пределах от 0° до 360°.

Сила лобового сопротивления с увеличением угла атаки тоже увеличивается, имея минимум на углах около 0°, причем увеличение это близко подходит к параболическому закону. В авиации важно иметь возможно ббльшую подъемную силу и возможно меньшее лобовое сопротивление; таким образом качество крыла оценивается

Q

величиной -γ*-· На

(а?

фигура 11 показано также изменение качества с углом атаки.

Из фигура 10 видно, что величина, обрати.

С_х

качеству, то есть

Су есть tg угла наклона вектора полной силы к подъемной силе; этот наклон имеет нек-рый минимум, соответствующий наибольшему качеству, после чего он начинает опять увеличиваться. При угле атаки, соответствующем нулю подъемной силы, вектор полнойсилы обращается в лобовое сопротивление и направлен по потоку. Центр приложения вектора полной силы также меняет свое положение, причем при наибольшей подъемной силе, то есть при критическом угле, он расположен обычно в наиболее переднем положении (обычно около Vs ^от передней кромки), с уменьшением же угла атаки точка приложения отходит назад (фигура 12). Полная сила сопротивления образуется за счет разных скоростей по профилю крыла, а следовательно, и разных давлений в этих местах. Как показывает опыт, давление по профилю распределено т. о., что разрежение с верхней стороны больше, чем давление снизу; т. о. крыло поддерживается в воздухе главн. обр. не давлением снизу, а присасыванием сверху. С уменьшением угла атаки в передней части профиля начинает появляться сила, противоположная получающейся в задней, и при угле атаки, соответствующем нулю подъемной силы, эти две силы становятся равными и противоположными. Следовательно, при нуле подъемной силы имеется не только лобовое сопротивление, но также и еще пара сил, которая стремится повернуть крыло на еще меньшие углы. Т. о. мы видим, что при набегании на крыло потока с определенной скоростью на крыле получается сила сопротивления, которая относительно какой-либо точки на крыле дает момент. Обычно для удобства этот момент относят к носику профиля, то есть при цилиндрическом крыле — к точке пересечения хорды

Фигура 12. Положения равнодействующей на профиле крыла. профиля с перпендикуляром к ней, касающимся передней кромки. Момент относительно передней кромки будет

М=C„QSbv², (8)

где С_т —т. н. коэфф. момента, а b — длина хорды профиля — ширина крыла (в случае нецилиндрических крыльев момент относят к какой-либо точке крыла, например к наиболее выступающей вперед кромке и тому подобное.). Коэфф. момента наносится на общую диаграмму. Эта диаграмма, на которой нанесены в зависимости от углов атаки коэфф-ты подъемной силы, лобового сопротивления, момента и иногда качество, называется характеристикой данного крыла. Иногда более удобными бывают характеристики несколько иного вида: по оси абсцисс откладывается коэффициент лобового сопротивления, а по оси ординат — коэффиц. подъемной силы, углы же атаки наносятся на самой кривой как параметры; такого вида характеристика называется полярой Лилиенталя 1-го рода; она представляет удобства в том отношении, что на ней сразу находятся и полная сила, и ее направление, и качество; последнее будет tg угла наклона прямой, проведенной из начала координат к определенной точке кривой, соответствующей данному углу атаки (смотрите фигура 13). Очень часто, для удобства построения поляры, масштабы осей орди-

Фигура 13. поляра Лилиен- нат и абсцисс при-таля i-го рода. нимают разными

(обычно масштаб О_х берут в пять раз больше, чем масштаб С_у); в этом случае при нахождении качества и вектора полной силы приходится принимать во внимание разные масштабы. В вопросах устойчивости аэропланов часто приходится находить коэфф-ты сопротивления компонентов сил не по направлению потока и ему перпендикулярному, а по хорде крыла. В этом случае .получаются два компонента:

Л_п — C„qSv² и R_t=C_tgSv², где первая сила направлена по перпендикуляру к хорде, а вторая—по хорде. Если построить диаграмму, исходя из этих сил, т.е. откладывая их соответственно по оси ординат и абсцисс, то получится поляра Лилиенталя 2-го рода. Также и здесь, •для удобства построения, масштабы осей координат иногда принимаются разными.

Вид характеристики в значительной мере зависит от формы профиля, однако можно подметить некоторую закономерность в течении того или иного элемента характеристики. Так, например, профиля с большой кри визной обычно имеют бблыную подъемную силу, следовательно и бблыную максимальную подъемную силу; последняя величина чрезвычайно важна для аэропланных крыльев; с другой стороны, тонкие кривые профиля имеют быстрый срыв струй на отрицательных углах. Толщина профиля играет до некоторой степени роль кривизны, то есть можно сказать, что толстый профиль, имеющий одинаковую среднюю кривизну (то есть кривизну лмми, делящей пополам разность ординат верхней и нижней линий очертания профиля), до некоторой степени подобен тонкому профилю с такой же средней кривизной; однако толстые профиля обычно имеют более плавную поляру в диапазоне практически применяемых углов атаки. Профиля симметричные, то есть с нулевой средней кривизной, имеют сравнительно небольшой прямолинейный участок на кривой подъемной силы, то есть срыв струй у них наступает уже при сравнительно малых углах. Помещение на одном крыле разных по размаху профилей, а также установка этих профилей под разными углами (сложные крылья) могут значительно изменять аэродинамич. характеристику всего крыла по отношению к характеристикам входящих в это крыло профилей. К этому виду сложных крыльев относятся также и сдвоенные или строенные крылья, расположенные или одно над другим, или одно сзади другого; в первом случае мы имеем бипланы и трипланы, а во втором—тендемы. За последнее время теория таких сложных крыльев довольно хорошо разработана (смотрите Индуктивное сопротивление), и поэтому систематического испытания их в аэродинамических трубах почти не производят, кроме испытаний в уже готовых аггрегатах — моделях аэропланов.

Аэродинамические исследования разделяются на два типа: на качественные и количественные. В первом случае явление исследуется с чисто формальной стороны, не затрагивая измерения элементов, вызывающих или сопутствующих данному явлению. К ним относится снятие аэродинамических спектров. Во втором случае измеряются те силы и скорости, которые в данном объекте исследования появляются. Снятие спектров производится различными способами. Пуская цветной дым в поток, набегающий на исследуемую модель, можно соответствующим образом зафиксировать на фотографической пластинке линии токов этого течения. В 1909 г. японский проф. Танака-дате производил опыты со снятием спектров потока вокруг вращающегося винта, впуская к лопастям нагретый воздух и фотографируя видимые вихри. За последнее время в Америке были получены спектры потоков, обтекающих модели крыльев с почти звуковой скоростью. Фотография получалась благодаря большому изменению плотности вокруг крыла и конденсации водяных паров, содержащихся в воздухе. Д. П. Рябушинский в Аэродинамической лаборатории в Кучине получал спектры помощью ликоподия (фигура 14). Одним из наиболее простых способов

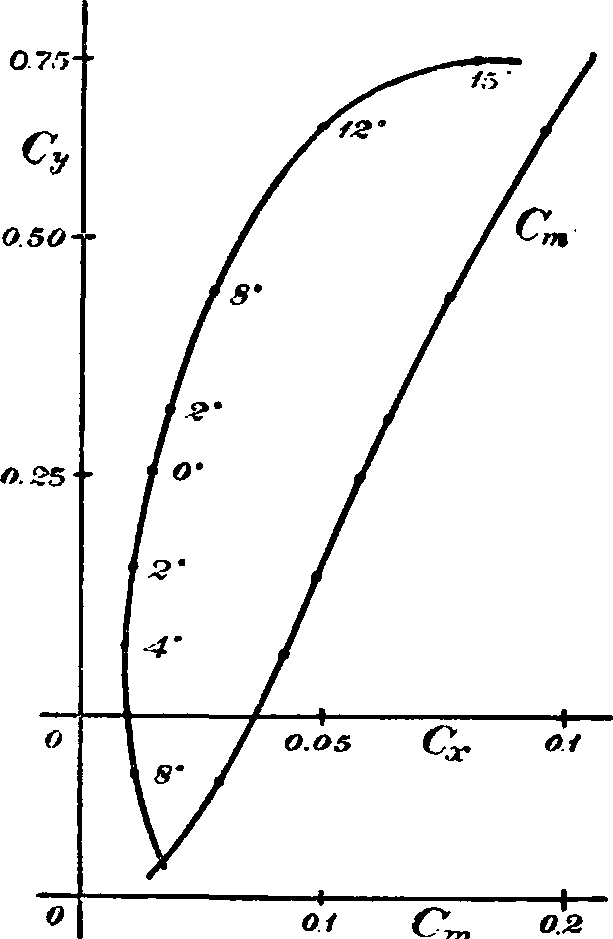
получения спектров является помещение в потоке ряда маленьких флажков и фотографирование нх направления. Кроме получения спектров в воздухе, гораздо легче получаются спектры в воде путем подкрашивания впускаемых струек (Хейль-11 Iay-Карефоли).

Количественные исследования могут производиться двумя путями. Для определения величины сопротивления потока на

Фигура 14. Спектр Рябушипского. Обтекание плоской пластинки. тело можно или тело двигать в жидкости, или, наоборот, создавать движущийся поток, набегающий на неподвижное тело. В первом случае необходимо испытуемое тело двигать или прямолинейно, например на какой-нибудь тележке, поставленной на рельсовый путь (тележка Saint-Syr), или же на автомобиле (опыты Duc de Guiche), или по кругам, — вращая его на конце рычага около укрепленного центра (ротативная машина). Однако такого рода исследования на открытом воздухе распространения не получили, вследствие того, что движение тела в неспокойном воздухе не позволяет создать обстановки, в которой можно было бы учесть влияние различных факторов на точность измерения,— в закрытом лее помещении трудно создать необходимые скорости. Поэтому в настоящее время при аэродинамич. исследованиях почти всегда пользуются вторым путем, оставляя тело неподвижным и создавая движущийся поток. Этот поток получается в аэродинамических трубах (смотрите ниже), и самые исследования производятся в аэродинамических лабораториях. В виду того, что создание в аэродинамич. трубе цилиндрического потока большого диаметра и большой скорости требует затраты большой мощности, исследования в аэродинамическ. трубах ведутся обычно на сравнительно малых моделях. Т. к. весьма часто аэродинамич. исследования, произведенные на моделях, приходится применять на практике для больших объектов, должен возникнуть вопрос о возможности применения выведенных зависимостей к большим объектам. Закон аэродинамическ. подобия говорит, что при соблюдении одинаковости числа Рейнольдса можно считать течения подобными, а следовательно, и коэфф-ты сопротивления, найденные в одном случае, применять в другом. Оперируя в одной и той же среде, числитель дроби, выражающей число Рейнольдса, vl, называют характеристикой опы-

т а. Обычно в аэродинамических трубах испытывается модель аэропланиого крыла в 7ю—V20 натуральной величины; следовательно, чтобы выдержать числа Рейнольдса, получающиеся в натуре, необходимо иметь скорость в трубе в 10—20 раз большую, что, конечно, чрезвычайно затруднительно. Т. о., с точки зрения применения экспериментальной А. для практических целей авиации, можно говорить лйшь о пределах чисел Рейнольдса, при которых следует производить аэродинамич. испытания. Вопрос еще усложняется при испытании моделей, имеющих различные линейные размеры своих элементов, — в этом случае модели испытываются по большей части без мелких деталей (например без проволок-растяжек, тонких стоек и тому подобное.); эти детали испытываются в натуральную величину при скоростях полета аэроплана, и их сопротивление прибавляется к сопротивлению, полученному при испытании модели. Этим делается допущение независимости аэродинамического действия отдельных деталей. В натуре характеристики опыта для аэропланных крыльев обычно бывают в пределах 50—150 м²,1ск, в аэродинамич. же трубах — ок. 6—30 м²/ск; следовательно, эти числа далеки от действительно наблюдаемых. Для выяснения пределов применимости испытаний при малых характеристиках опыта, производятся также испытания целых аэропланов в полете. Как оказывается, наибольшее расхождение получается при углах атаки, близких к критическим, причем б. ч. наблюдается в моделях более раннее наступление срыва струй, чем в натуре, а следовательно, и меньшее значение максимальной подъемной силы для тонких крыльев, и обратное— для толстых. Для соблюдения числа Рейнольдса, в Америке была выстроена аэродинамическ. труба с сжатым воздухом, где давление доводилось до 20 atm и этим увеличивалась плотность воздуха. Вследствие уменьшения кинематического коэффициента вязкости воздуха с увеличением плотности, в этой трубе достигались характеристики опыта порядка 50 м^г1ск. Как показывают имеющиеся в настоящее время исследования, при характеристиках опыта приблизительно в два-три раза меньших, чем в натуре, расхождение получается, повидимому, порядка 10% на участках характеристик крыльев, не близких к критическим положениям (малые и большие углы атаки). Что касается лобового сопротивления различных тел, то для хорошо обтекаемых тел пределы чисел Рейнольдса гораздо значительнее, чем для тел плохо обтекаемых. Вообще зависимость сопротивления от числа Рейнольдса недостаточно хорошо изучена, и поэтому в настоящее время нет еще достаточно четкого критерия для перехода от модели к натуре. Обычно полагают, что модели, испытанные при характеристиках опыта выше 6 м^а/ск, дают результаты, которые можно применять и к аэропланам в натуре.

В связи с запросами конструирования новых типов аэропланов, аэродинамич. исследования моделей широко применяются в изучении свойств аэроплана и его деталей, как-то: в определении его статической устойчивости, эффектов действия органов управления, исследовании винтов и тому подобное. У нас в СССР всякая вновь сконструированная машина, до выпуска ее в первый полет, должен быть испытана в виде модели в аэродинамической трубе на устойчивость.

Кроме нахождения сил, действующих на тела, помещенные в поток, аэродинамическ. исследования касаются также нахождения распределения давления около этих тел, определения скоростей в потоке, то есть нахождения т. н. скоростного поля, и тому подобное. Эти исследования производятся как в аэро-динамич. трубах с моделями, так и с действительными объектами в натуральную величину. Примером последнего может служить нахождение распределения давления по крыльям летящего аэроплана, которое находится путем дренирования крыльев аэроплана и записью соответствующими манометрами, число которых иногда доходит до нескольких сот. Отдельно стоят аэродинамические исследования аэропланов в не-установившемся движении. Эти исследования ведутся гл. обр. с аэропланами в натуре и заключаются в нахождении помощью соответствующих приборов моментов и сил, действующих в этом случае на летящий аэроплан (смотрите Динамика полета).

Экспериментальная А. применяется во многих отраслях техники, но наибольшее применение она получила в авиации — в теории аэроплана. В аэроплане часть элементов имеет лобовое сопротивление и подъемную силу, а часть —только лобовое сопротивление. Т. о. если к лобовому сопротивлению крыльев прибавить лобовое сопротивление других частей аэроплана, то мы получим полное лобовое сопротивление аэроплана. Обычно подъемной силой других частей, кроме крыльев, пренебрегают; т. о. можно получить характеристику уже всего аэроплана, если к характеристике крыльев прибавить это полное лобовое сопротивление (Сое== С_х + С_х). Если предполагать также, что от угла атаки это добавочное лобовое сопротивление не зависит, то поляру Лилиенталя для всего самолета мы получим, отодвинув всю кривую II оси ординат на эту добавочную величину

(фигура 15). Отношение Фигура 15. Поляра Лшгаен- q

-Д- будет качеством Оа

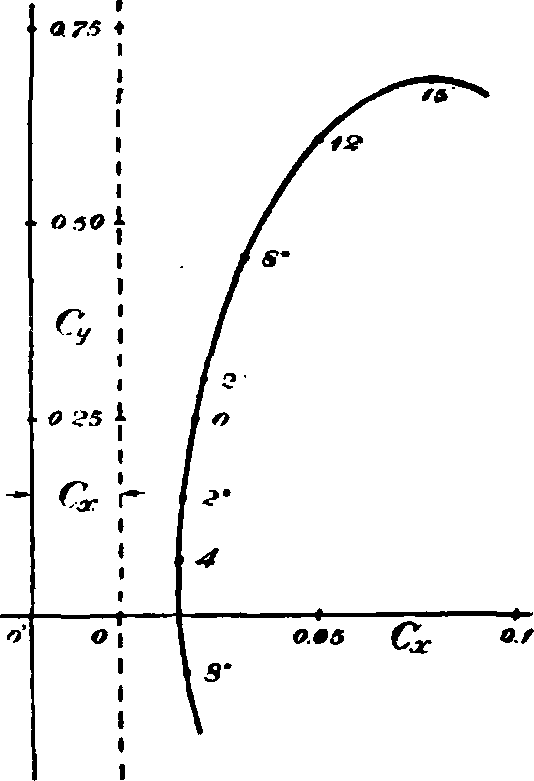
таля всего самолета. всего аэроплана; его можно найти, проведя лучи из начала к соответств. углам на поляре (при одинаковых масштабах осей координат). Максимальное качество равно tg угла наклона касательной, проведенной из начала координат (обычно это качество изменяется для различных аэропланов в пределах от 6 до 12).

На аэроплан в равномерном установившемся горизонтальном полете (фигура 16) действуют силы: 1) вес аэроплана G, 2) подъемная сила аэроплана Р, 3) лобовое сопротивление Q и 4) сила тяги винта Ф. При указанных условиях полета равнодействующая всех сил и момент относительно центра тяжести аэроплана должен быть равны

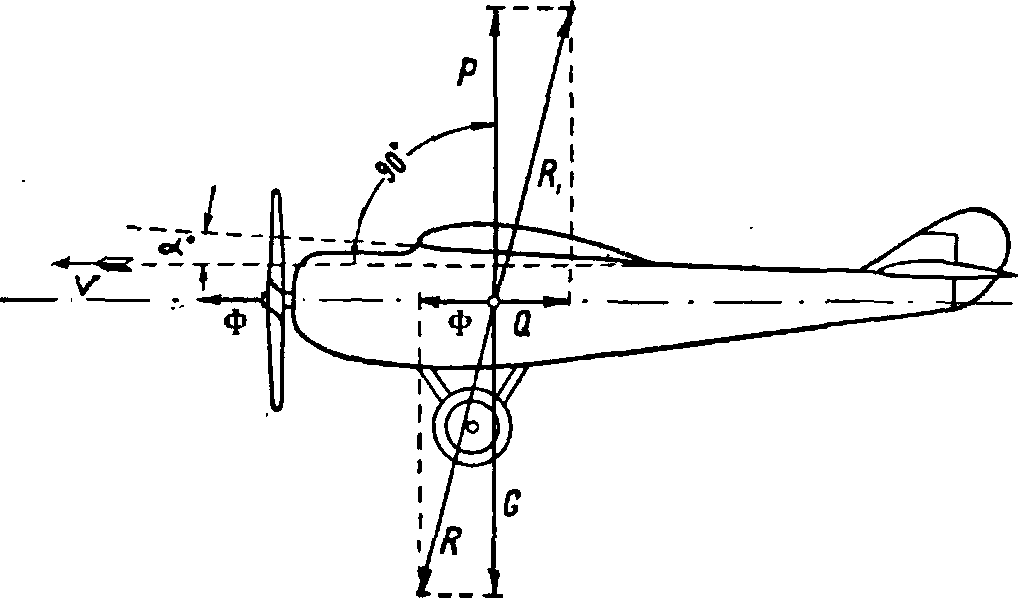
Фигура 16. Схема усилий в горизонтальном полете аэроплана. нулю. Б. ч. при аэродииамич. расчете моменты сил, вследствие их небольшой величины, не принимаются во внимание (т. к. предполагается, что летчик рулями устанавливает равновесие аэроплана), а рассматривают только равнодействующую сил. Т. о. надо, чтобы сила тяги была равна лобовому сопротивлению, а сила тяжести — подъем, силе; это приводит нас к условию: Ф=С ^qSv* (9)

и Р=(?= C_vqSv². (10)

Эти формулы являются основными формулами аэродинамического расчета самолета. Мощность в Н“, потребляемая аэропланом при горизонтальном полете на различных углах атаки, выразится:

= (и)

Вместе с предыдущим равенством (9) мы получаем тяги и мощности, потребные для горизонтального полета аэроплана. Можно, т. о., составить кривые тяги- и мощностей в зависимости от скорости полета для данного аэроплана, то есть аэроплана данного веса, аэродинамически определяемого соответствующей ему характеристикой, по формулам (9) и (И), принимая во внимание равенство (10), к-рое обусловливает горизонтальность полета. Такие кривые называются кривыми П э н о. Т. к. с высотой плотность воздуха меняется, то, изменяя ρ соответствующим образом (смотрите Атмосфера стандартная), или просто изменяя масштаб скорости, можно найти кривые Пэно и для разных высот. Кривые Пэно имеют минимумы как тяги, так и мощности. Угол атаки, при котором тратится наименьшая тяга для самолета при горизонтальном полете, называется наивыгоднейшим углом атаки, угол же, при к-ром тратится наименьшая мощность — экономическим углом атаки. Экономический угол атаки всегда больше наивыгоднейшего, поэтому и скорость, соответствующая наивыгоднейшему углу, больше экономической скорости. Движение аэроплана по наклонным к горизонту траекториям без тяги винта, то есть под влиянием составляющей силы тяжести, называется планированием. На фигуре 17 дано распределение сил при планировании под углом Θ к горизонту; как видим, угол планирования равен углу между полной силой сопротивления и подъемной силой, т. e. tg его равен

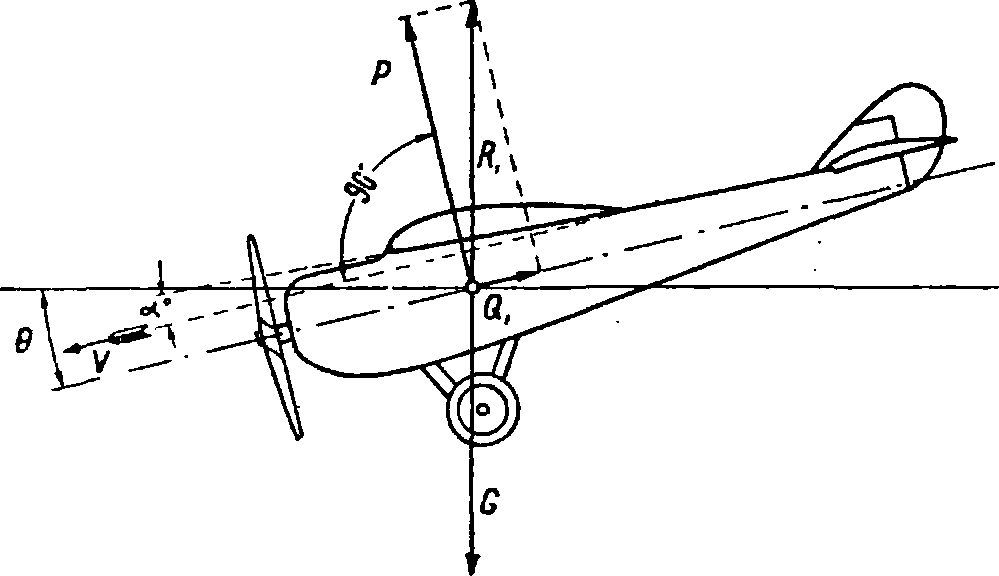
Фигура 17. Схема усилий в планирующем аэроплане. обратному качеству самолета, или он равен углу, составленному с осью ординат прямой, проведенной из начала к соответствующему углу атаки на поляре Лилиенталя для всего аэроплана. Минимальным углом планирования будет, следовательно, угол, составленный с осью ординат касательной, проведенной из начала к поляре Лилиенталя. Скорость планирования определяется из формулы: _

-/fey ⁽¹²⁾

где С_а находится из поляры для соответствующего угла планирования. При планировании под углом около 90°, когда подъемная сила крыльев равна нулю и все сопротивление сводится к лобовому сопротивлению, имеется случай установившегося пикирования. В данном случае Ra=G, и скорость пикирования находится из уравнения 6г=C₁fSv², где С_а соответствует значению С_р=0.

Основной прибор всякой аэродинамич. лаборатории—аэродинамич. труба—строится на основании соответствующих опытов и выводов экспериментальной А., которая дает необходимые для расчета коэффициенты, как качество трубы, коэффициенты трения воздуха о стенки и, следовательно, падение напора вдоль трубы и тому подобное. Аэродинамическая труба в основной своей части представляет цилиндрический канал, в котором помощью вентилятора создается поток воздуха значительной скорости (обычно 30 — 50 м/ск). Поместив в этот поток какое-либо тело (модель самолета, крыла и тому подобное.), можно наблюдать как течение воздуха (съемка спектра), так и те силы, которые текущий воздух вызывает на теле. Поток в такой трубе, для получения точных и однородных результатов, должен быть постоянен по времени и иметь в различных точках сечения одну и ту же скорость. Для получения такого потока перед цилиндрической частью трубы помещается плавно сходящийся насадок, «коллектор», в который вставлена направляющая решетка. Поверхность стенок трубы делается возможно более гладкой, и помещение, в котором нахо дится труба, строится с гладкими стенами, без ниш, выступов и тому подобное., благодаря чему получается минимальная, возможная в данных условиях, неравномерность потока, доходящая в хороших трубах по сечению лишь до 1—2%, а по времени до 0,5—1,5%. При конструировании труб вопрос об их экономичности имеет большое значение, и в настоящее время, когда мощность моторов на трубах превосходит 200 Н экономия в мощности является существенно важной. Все потери должен быть уменьшены. Коллектор, устраняя сжатие струи при входе, уменьшает потери, связанные с этим сжатием. Далее идут потери на трение в рабочей части, после чего воздух с полной рабочей скоростью выбрасывается из трубы и происходит явление удара, на к-рое тратится полностью вся живая сила. Эта потеря, весьма значительная, уменьшается во много раз применением расширяющегося канала — диффузора, к-рый с небольшими потерями обращает кинетическую энергию струи в потенциальную. Сумма всех потерь энергии должен быть пополняема двигателем, передающим свою энергию потоку посредством вентилятора с некоторым кпд η вент. Приравняв секундную энергию, отдаваемую вентилятором, энергии потерь и выразив последнюю в долях живой силы секундной массы воздуха в рабочем сечении, получим:

Σ» ^{т V2} ЦТ

ς —2— =А η вент.»

где ξ—коэфф. потерь на различных участках трубы, а N—мощность мотора в килограммахм.

mu*

Ч вент. п

Величина

Ц вент.

Ж

—Хтр. называется качест вом трубы. Принимая массовую плотность

1 Fv*

воздуха ρ= —, получаем: х_тр.= ₁₂ооЖ ’

где F— площадь рабочего сечения в ж², a Ν— мощность мотора в Н*.

А. т. можно разделить на 3 типа. Тип I (фигура 18)—незамкнутая А.т.,открытая с концов, с замкнутым потоком. Воздух засасывается из помещения, пройдя сквозь к-рое

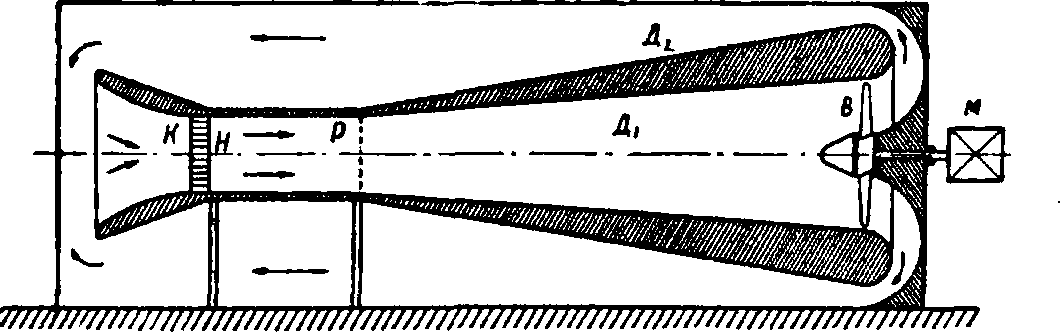
Фигура 18. Открытая труба (СССР—Англия): К— коллектор, Р−рабочая часть, Д„ Д,—диффузор,

В—вентилятор, М—мотор, Н—направляющая решетка. выбрасывается и по помещению возвращается обратно. Поток в рабочей части отделен от внешнего пространства стенками. Этот тип применяется в СССР и в Англии. Тип II (фиг“. 19)—незамкнутая А.т.со свободным потоком. Стенки рабочей части раздвинуты и образуют герметическую камеру (камера Эйфеля), к-рую и пронизывает поток.

Тип этот распространен во Франции. Тип III (фигура 20)—замкнутая труба со свободным потоком. Выходное отверстие связано со всасывающим герметическим обратным каналом. Поток в рабочей части открыт и сообщается с окружающим помещением.

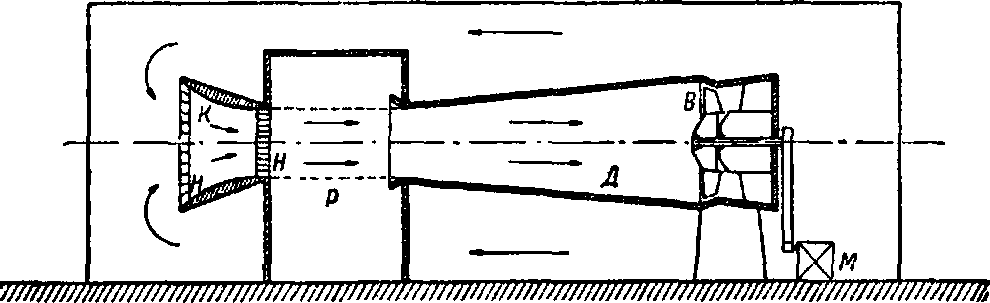
Фигура 19. Труба Эйфеля (Франция): К—коллектор, Р−рабочая камера, Д—диффузор, В—вентилятор, М— мотор, Н—направляющая решетка.

Давление в потоке атмосферное. Тип этой трубы применяется в Германии (труба Прандтля).

Измерение скорости потока в аэродинамической трубе, а равным образом и на аэроплане, производится, кроме тарированных анемометрических приборов-вертушек, также и манометрическим способом, путем измерения скоростного напора в потоке помощью разного вида насадок, обычно присоединяемых к различным манометрам.

Исследование аэродинамич. труб и применяемых в них лопастных вентиляторов дает возможность до некоторой степени применять эти выводы и к таким промышленным сооружениям, как вентиляционные каналы и коридоры в сушильнях, вентиляциях большого расхода и тому подобное. Старые

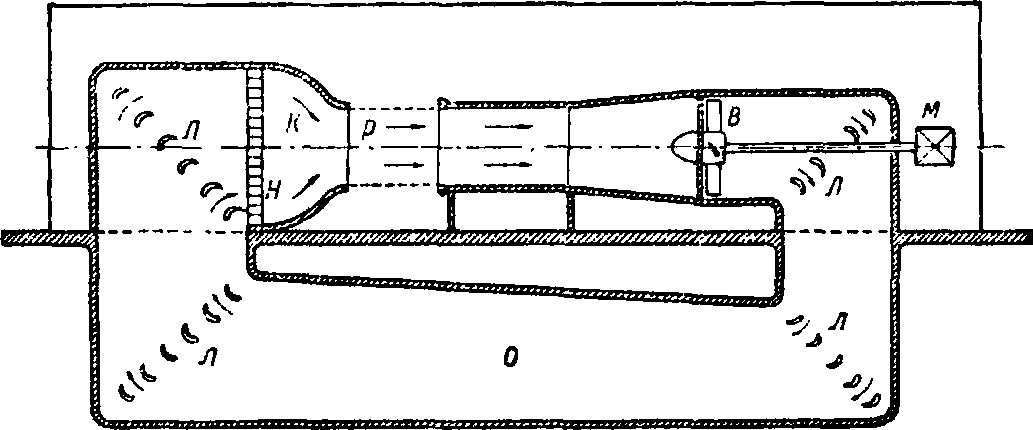
Фигура 20. Замкнутая труба Прандтля (Германия):

К—коллектор, Р−рабочая часть (открытая), В— вентилятор, Л—направляющие лопатки, О—обратный канал, М—мотор, Я—направляющая решетка. нормы давления на крышу здания от ветровой нагрузки давали эти давления положительными, то есть давящими на крышу сверху; однако опыты, произведенные в аэродинамич. лабораториях, показали, что на крышу здания действует гл. обр. присасывающий эффект (фигура 21); поэтому во многих случаях нормы эти имели преувеличенное значение, а следовательно, вели к перетяжелению конструкции и удорожанию, давая вместе с тем ослабление крыши на отрывание.—Аэродинамич. исследования охватывают также и определение давления ветра на другие гражданские сооружения, как, например, мосты, мачты, дымовые трубы и тому подобное. Вопросы, касающиеся защитных от снега ж.-д. щитов—их установки, относительной высоты и расстояния от полотна, изучаются помощью аэродинами-мических спектров моделей.таких устройств. Быстрое развитие и прогресс транспорта, заключающийся в увеличивающихся скоростях передвижения, приводят к необходимости учитывать сопротивление воздуха, которое с увеличением скорости получает преобладающее значение. Поэтому и приборам транспорта приходится придавать в некоторых случаях, для уменьшения

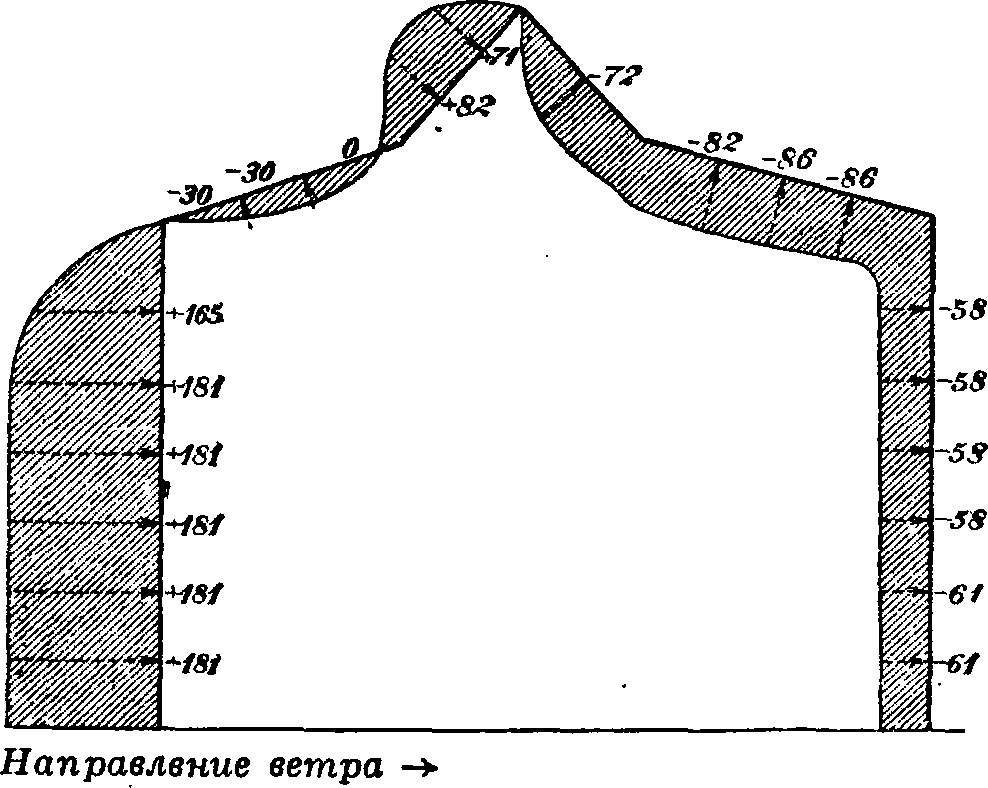
Фигура 21. Схема давления ветра на здания. сопротивления, аэродинамич. формы. Изучению подвергаются также кузова автомобилей, составы поездов и быстроходные корабли. В заключение необходимо упомянуть об аэродинамич. исследованиях ветряных двигателей (смотрите). Таким исследованиям подвергаются профиля, применяемые в лопастных ветряках, модели ветряков и т. д.

Лит.: Жуковский Η. Е., Теоретические основы воздухоплавания, изд. 2, М., 1925; С а т-к е в и ч А. А., Аэродипамика как теоретическая основа авиации, изд. Студ. б-ки Ин-та инж. пут. сообщ., П., 1923; Голубев В. В., Теория крыла аэроплана в плоскопараллельном потоке, Труды ЦАГИ, вып. 29, М., 1927; Аппель П., Руководство теоретической (рациональной) механики, т. 1—3, пер. с франц., М., 1911; Р г б 1 I Art., Flugtechnik.—Grundlagen des Kunstfluges, Munchen, 1919; Drysdale C., Mecanical Properties of Fluids, N. Y., 1923; Fuchs R. u. Hopf L., Aerodynamik, Handbuch d. Flugzeugkunde, Berlin, 1922; Lamb H., Hydrodynamics, Cambridge, 1924; G 1 a u e г t H., The Elements of Aerofoil a. Airscrew Theory, Cambridge, 1926; Bairstow L., Applied Aerodynamics, L., 1929. В. Александров.

® · Алмаз (карбонат)
4 ♦ Корунд
А А Наждак
V Карборунд, алунд и др.
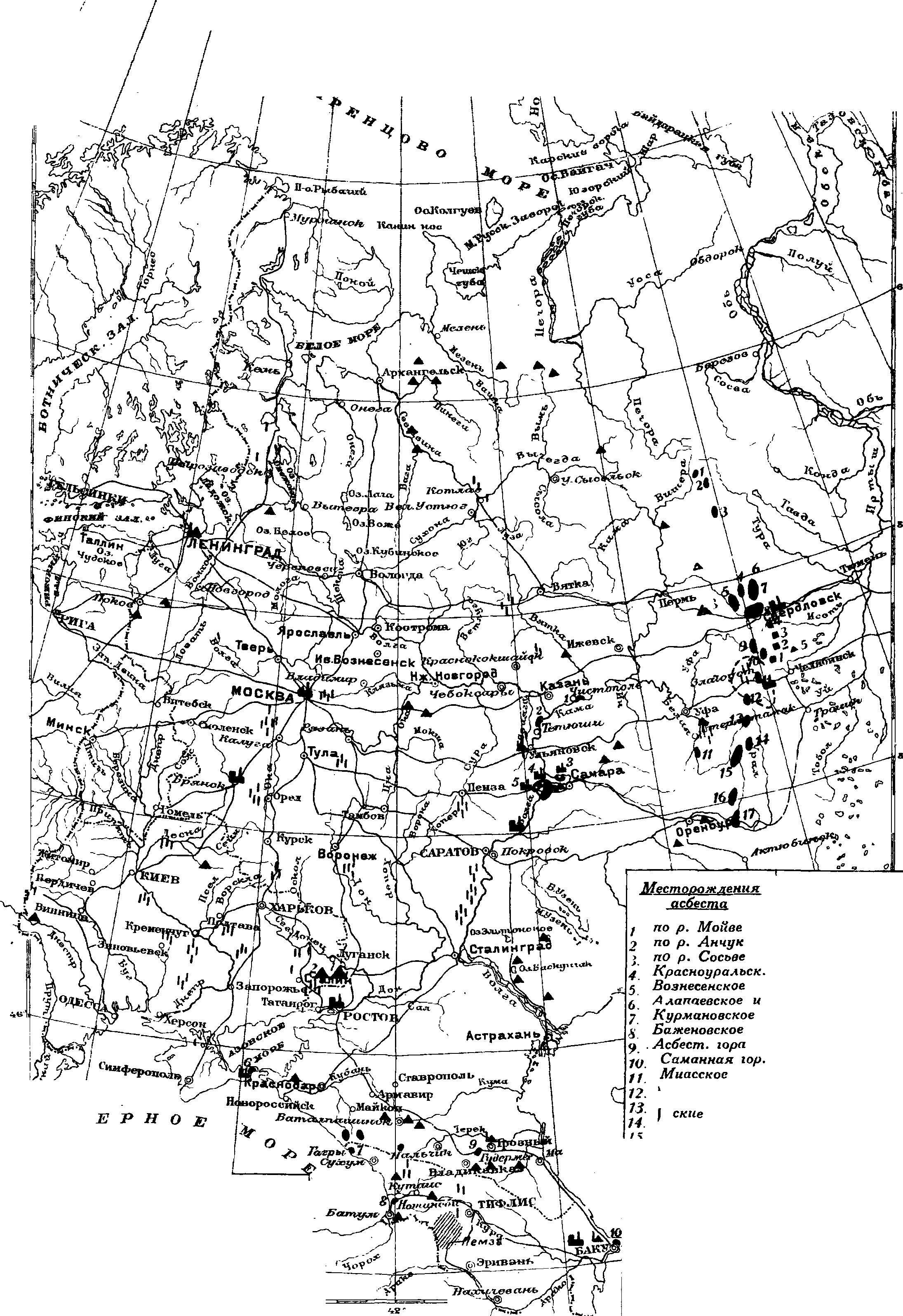
В Асбест.	(производство)
в Я Асфальт	натуральный
	битуминозный
□ □	нефтяной

Крупные значки указывают на мировое месторожд. Малые—на государств.

т. э.

Проф. М. Силищенский.

Награеироеаяо Корто

Алмазов Z.UUU.UW карат »1 Корунда в тоннах [ю] Наждака „

Карборунда Асбеста в тыс. тон.

0 Асфальта „ „

it Крупн. добыча связанного азота из воздуха.

Месторож. и добыча селитры.

Т"

¹

•m»V ^ Д

C* *

Hv°‘

Υ-ν

~-.J*y S/^PpcoH

^< ’^ИИИ>ОПО ^Севастолп.|_ГЬ«5

Асбеспщ^ Асбошиферн q

Асботекстильк. ® ·» Асфальтовый камень U. Асфальт нефтяной Корунд

* Наждак ^

▲ Алебастр, шпс ||1| Г Точильный камень -Д _N 1 Жерновой V jt

ч“·,¹ Тальк *

fy>cc&iipOQ.Qlfirpnboicj0am,.J£KJi,rf. 7?С.Ф,С.Р

Миасскос

I Верхнеураль-I скне г. Ирендык _по р У,-Зелаир /7 У А«Р· Песян-чиноЯ

Месторождения кооинда

1 Ильменск. горы Кизьглташское ^J Теченское "* Борзоаское Теченское

(нажд.)

Месторождения

1. Чистопольское (гудрон, песчан.)

2. Тетюшское (би-тумин. извести.)

3. Бахиловский з. (гудрон, песчан.)

4. Первомайск. з. (асфальт, ком.)

5. БатраКский з. (асфальт, кам.)

6. Керченское и Керченский зав.

7. у г. Гагры

8. у cm. Нотане-

L

9. у cm. Гудермес 10 А пшеронское 11. Стерлита

Месторождения и заводы Артемовское 2. Крематорское J. Ашанск. завод

Т. э.

Проф. М. Силкщенский.

Масштаб 1:20 ооо.ооо

inno Лет ВТУкм.тае.ДунАЕвА Москва