> Техника, страница 18 > Балки неразрезные

Балки неразрезные

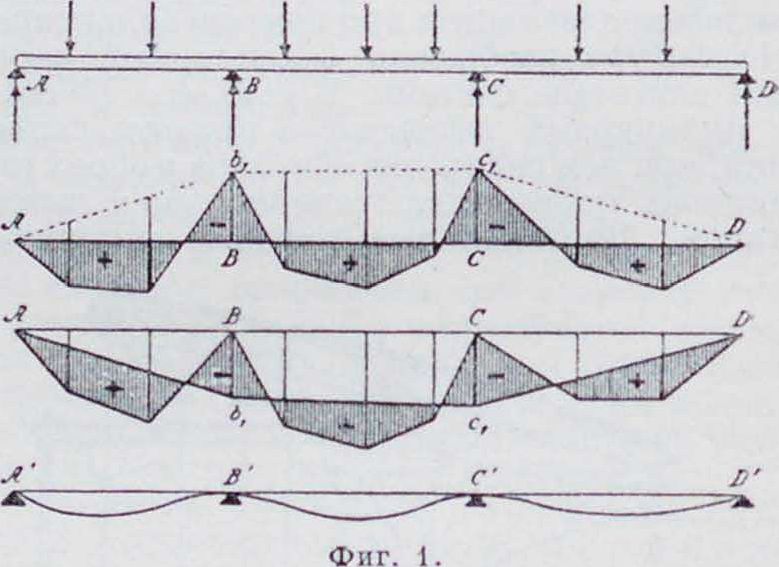
Балки неразрезные, балки, перекрывающие, не прерываясь, более одного пролета. Они встречаются в мостостроении и в гражданских сооружениях и особенно часто в сооружениях из железобетона. Они экономичнее, чем простые разрезные балки с такими же пролетами, и требуют менее широких промежуточных опор. Балки неразрезные не рекомендуются при ненадежном грунте, так как в них появляются дополнительные напряжения от неравномерной осадки опор.

В смысле расчета различают свободно лежащие Б. н. (с шарнирными опорами), которые могут свободно вращаться на опорах, и Б. н. упруго защемленные в опорах, где вследствие жесткой связи между балками и опорами последние принимают участие в упругой деформации. В обоих случаях можно различать еще балки неразрезкые с постоянными и переменными моментами инерции.

Графический расчет наиболее употребителен в настоящее время, т. к. он лучше удовлетворяет требованиям практиков, чем аналитический, который является чисто вычислительным методом.

Графический расчет.

I. Свободно лежащая балка с постоянным моментом инерции.

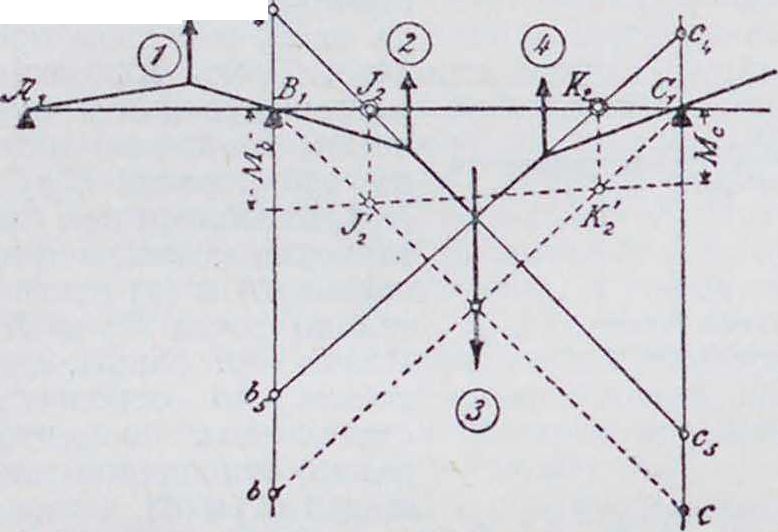
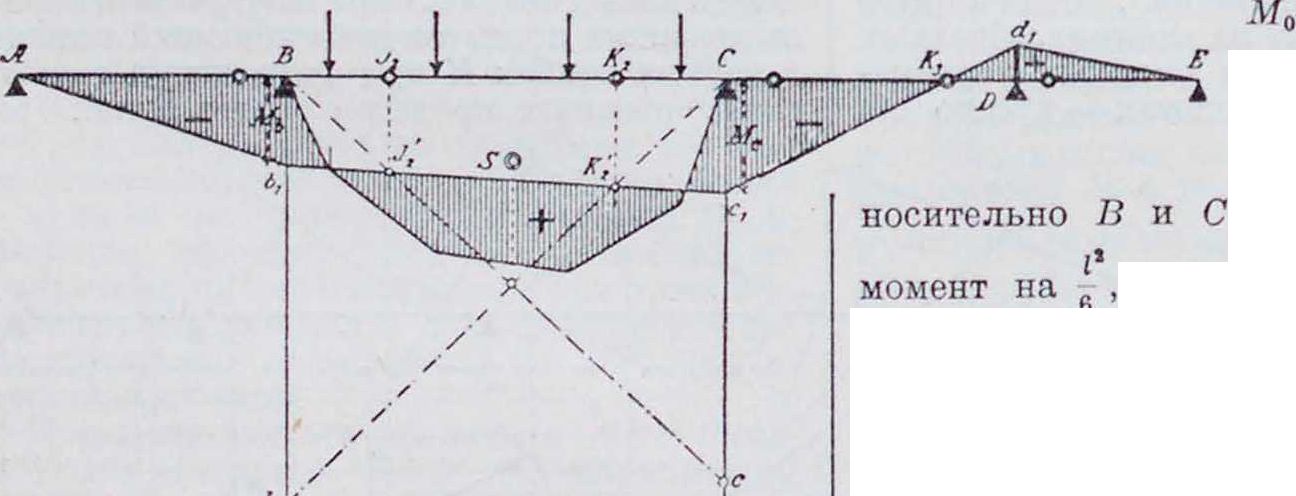
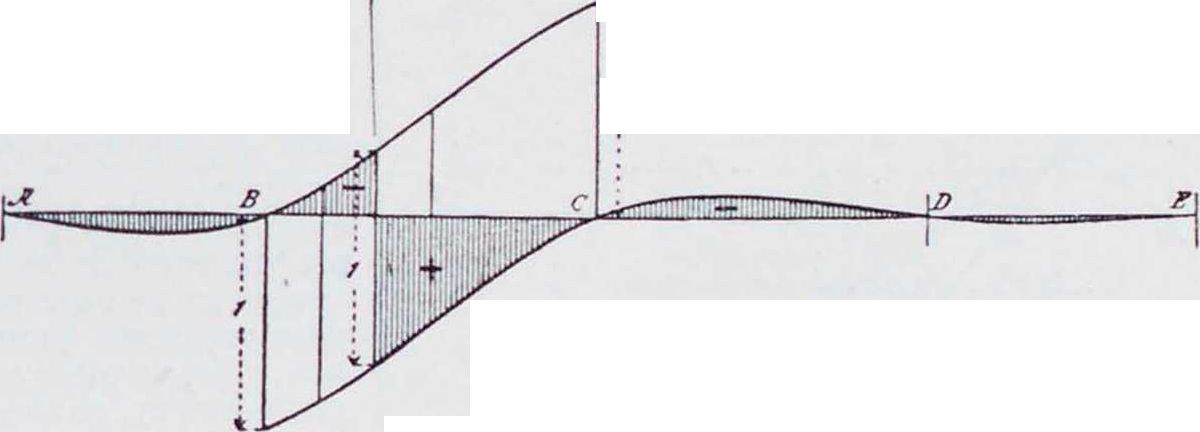
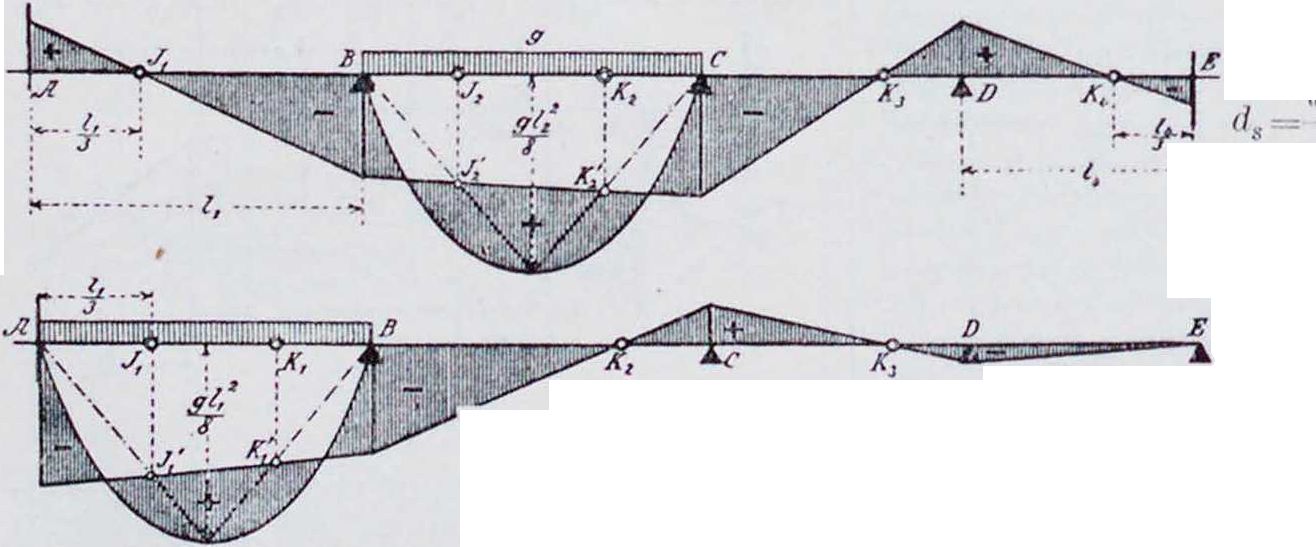
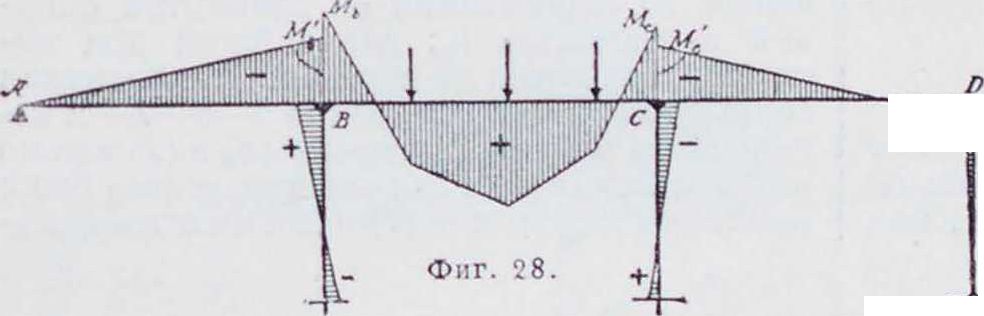
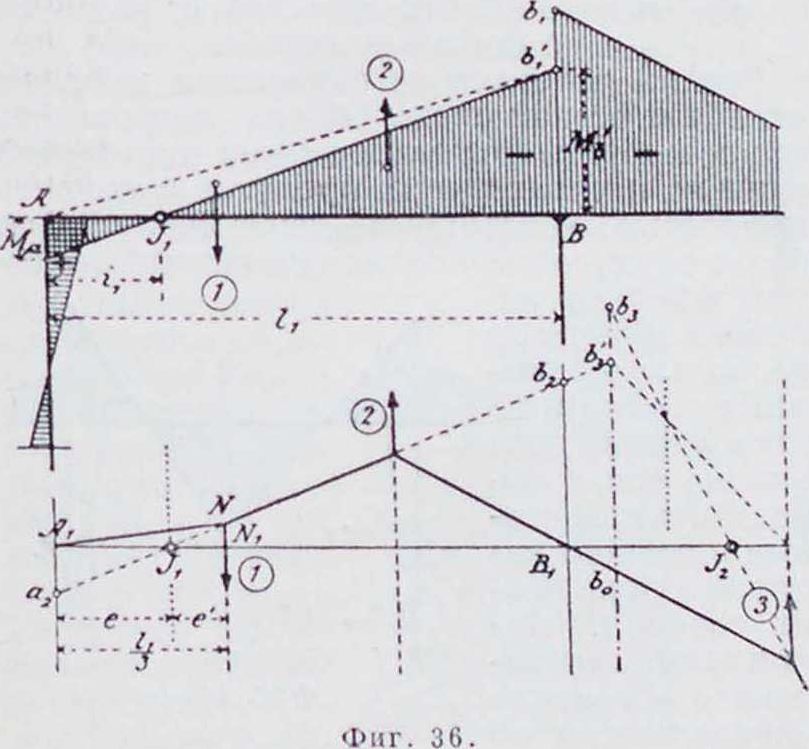
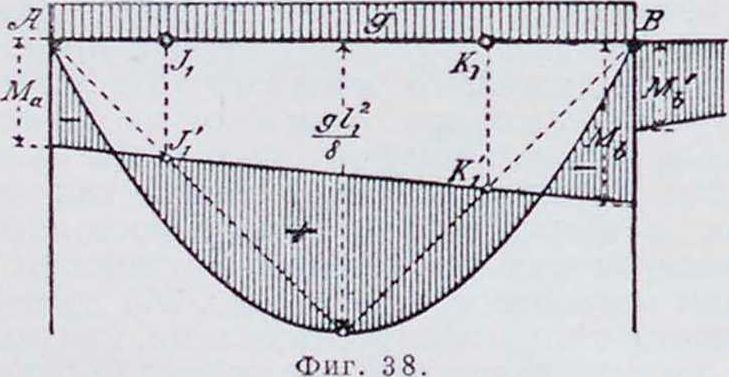
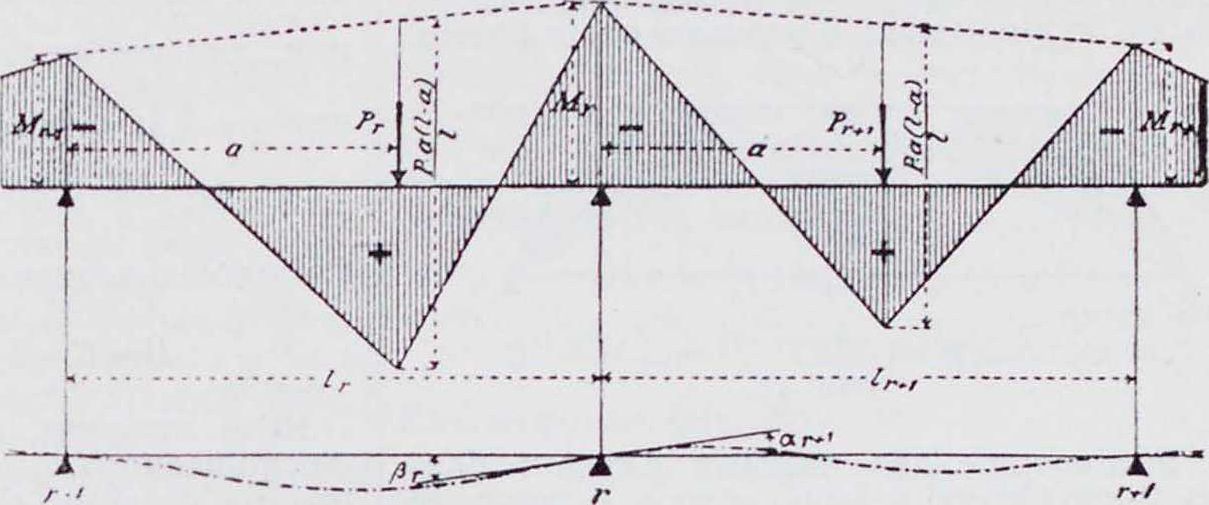
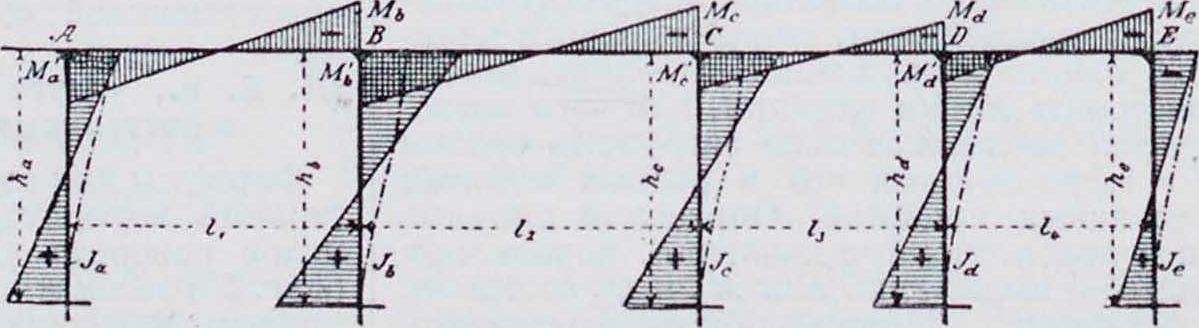
1. Эпюра м о м е н т о в Б. н. может быть построена при помощи веревочного мн-ка и замыкающей к нему,—как для простой балки, лежащей на двух крайних опорах Λ и I), если в число внешних сил будут введены реакции промежуточных опор II и С. Части этого веревочного мн-ка, ограниченные замыкающими Ab_lt b₃cj, C₁D, представляют собой эпюры моментов отдельных пролетов, как в случае балок,свободно лежащих на каждой опоре. Построив для каждого пролета от заданной нагрузки эпюры М₀книзу от горизонтальной прямой AD, можно получить эпюру моментов для Б. н., проведя замыкающую Ab_xc_xD, имеющую ординаты под опорами, равные опорным моментам (фигура 1). Следовательно, для построения эпюры моментов Б. н. необходимо определить опорные моменты. Степень статической неопределимости Б. и., свободно лежащей на опорах, из которых все, кроме одной,—подвижные, равна числу промежуточных опор.

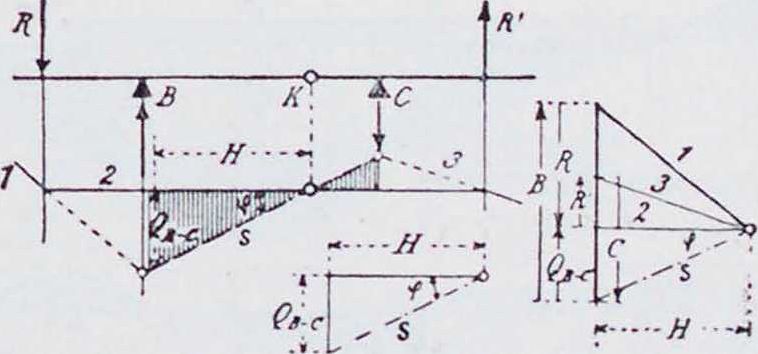
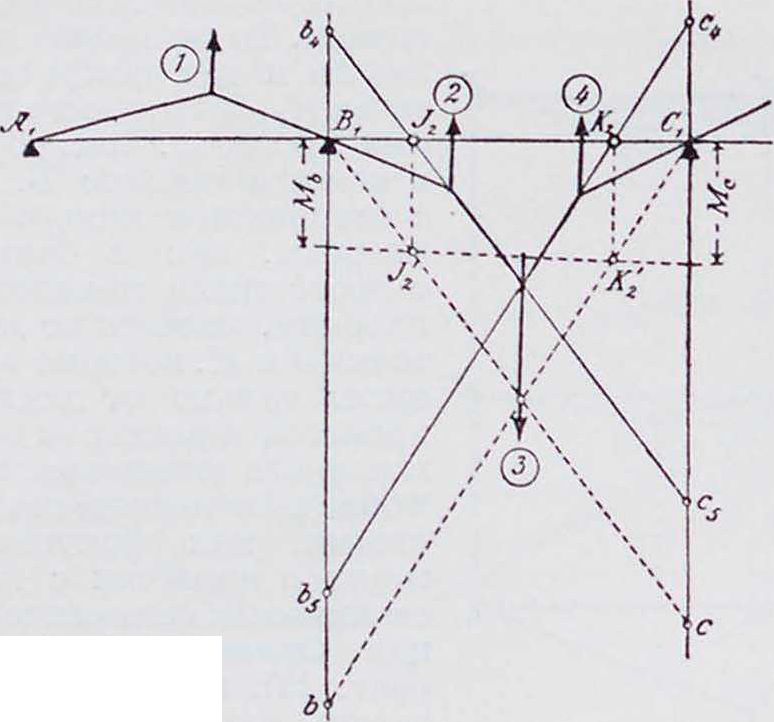
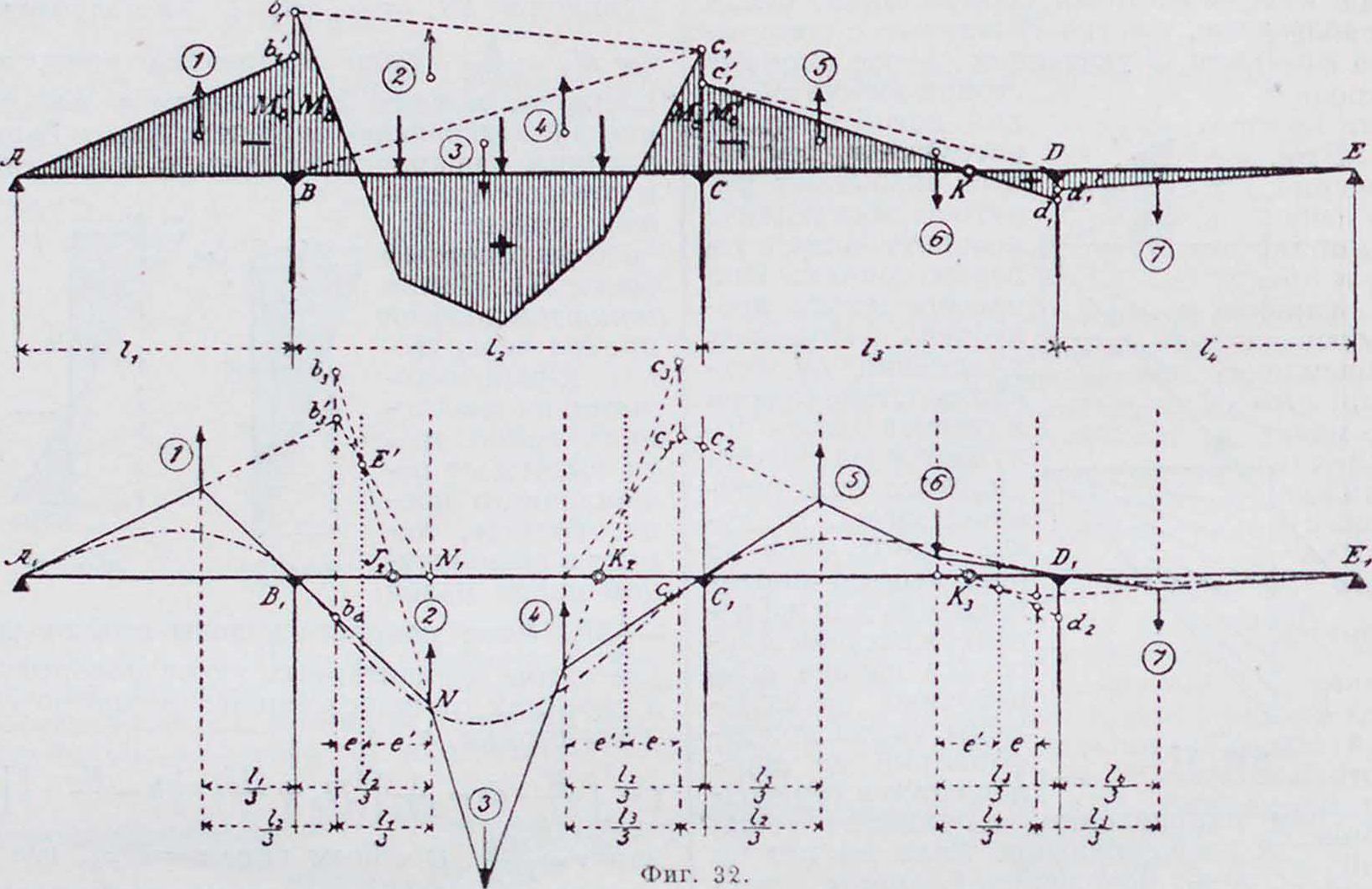
2. Фокус ы. Изгиб Б. η. между крайними опорами должен быть таков, чтобы упругая линия проходила через точки II и C на промежуточных опорах. По Мору (Mohr), упругую линию можно получить как веревочный мн-к для балки, лежащей на крайних опорах А. и Е (фигура 2) и нагруженной между ними площадью _]ч. 1ак как EI постоянно (Е—модуль упругости балки, 1 момент инерции поперечного сечения), то за фиктивную нагрузку принимается площадь эпюры моментов, что и сделано в дальнейшем. На фигуре 2 моментная площадь разбита по пролетам; загружен только второй пролет. Все участки от (ί) до (7), исключая площади М₀(3),—тр-ки, линии центров тяжести которых проходят на расстоянии одной трети пролета от опор. Площадь вывернутой трапеции в пролете 1₃ получится, как разница между отрицательным тр-ком (5) и положительным (б). Если для заштрихованной площади фиктивной нагрузки построить второй веревочный многоугольник Л!—с горизонтальной замыкающей А,В, то истин, точки упругой линии получатся только против границ отдельных площадей нагрузки, и т. о. точки пересечения В_1г О, Ε>! замыкающей со сторонами веревочного-

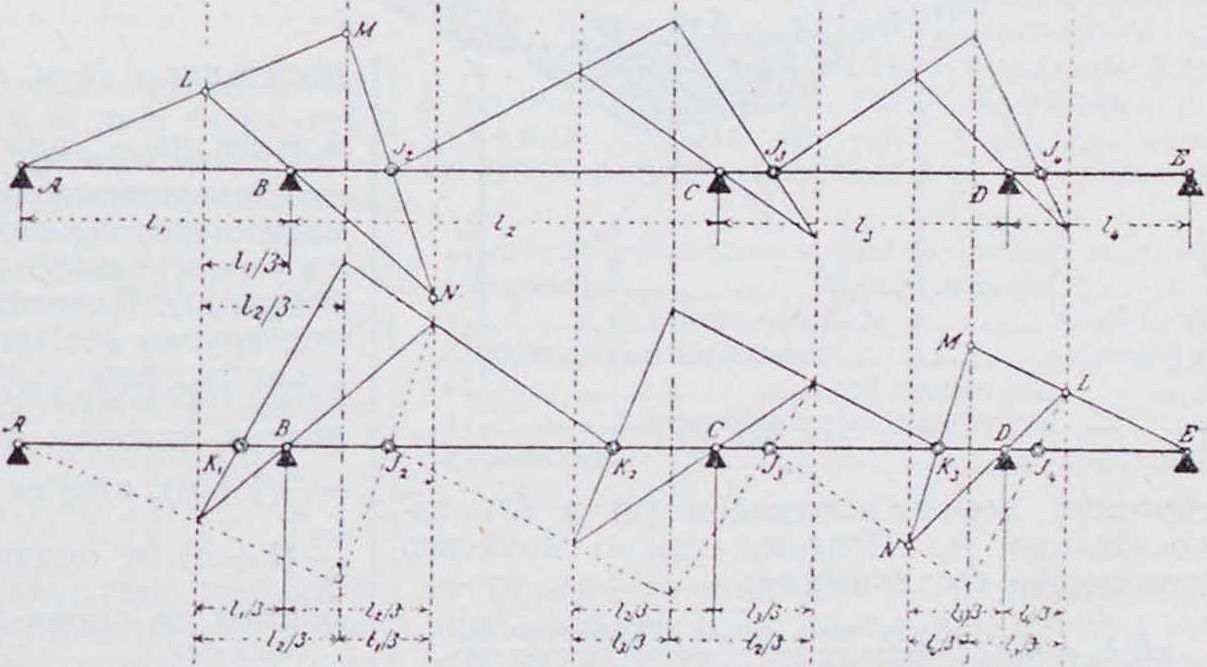
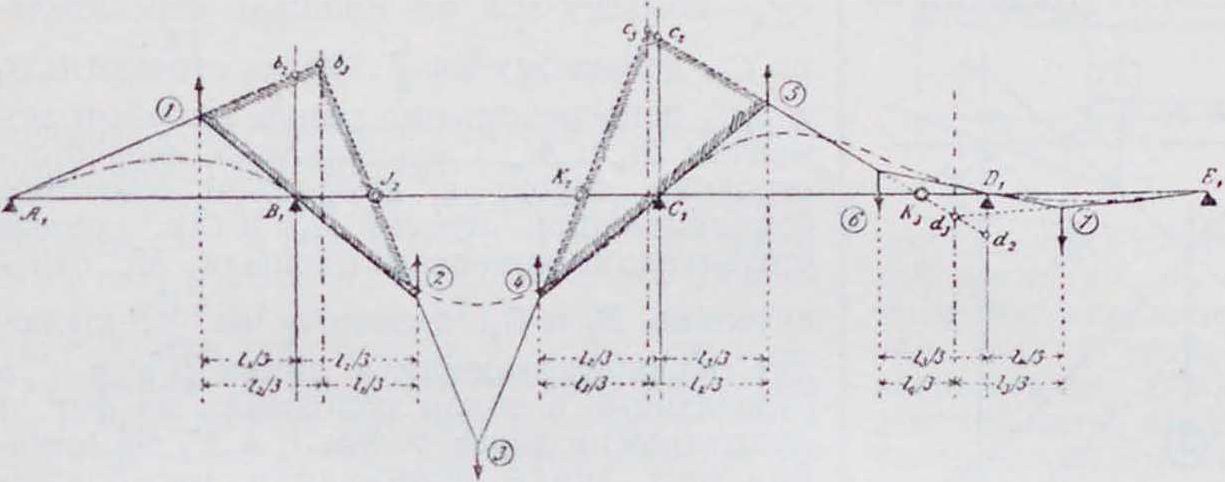
многоугольника должны лежать на опорных вертикалях. Кроме того, стороны веревочного мн-ка являются касательными к упругой

(5)—(6‘) проходит также через постоянную точку К₃. Проводя тот же анализ для тр-ка, образованного сторонами веревочного мн-ка (3) — (4), (4) — (5) и (5)—(6) с вершинами в обеих третях пролетов и на «сдвинутой опорной вертикали», и сторонами, проходящими через постоянные точки С и К₃, заключаем, что сторона (3)—(4) также должна пройти через постоянную точку К_г.

Если загрул:ен не 2-й, а 1-й пролет, то определяется еще одна постоянная точка Ку слева от By в первом пролете. Точка Кз совпадает с нулевой точкой линии моментов, потому что отрезки С с₂ и Dyd₂ относятся как статические моменты площадей (5) и (б) относительно точек Су и Dy. Плечи сил равны, следовательно отношение статических моментов равно отношению площадей (5) и (б), а именно Ссу : Ddy ·=Ссу: Ddy. Аналогично,

при загрузке одного 1-го пролета, момент в точке К₂ был бы равен нулю, в случае же загружения 3-го или 4-го пролета был бы равен нулю момент в точке J₂. Отсюда вытекает следующее положение: в каждом пролете Б. н. есть две постоянные точки: левая—J и правая—К; положение их зависит: первой— только от величины пролетов, слева от нее лежащих, и второй—от величины пролетов, справа от нее лежащих. Изгибающий момент в левых точках J при загружении справа лежащих пролетов и изгибающий момент в правых точках К при загружении только слева лежащих пролетов равны нулю. Ле

Фигура з.

Фиг. линии на опорах. Поэтому этот веревочный мн-к называют также упругим тангенциальным мн-ком. Вершины углов его лежат на неизменных вертикалях, проходящих через ц.т. площадей эпюры М₀. Кроме того, вертикали, проходящие через точки b₃, с₃, d₃, также остаются неизменяемыми, так как соответствуют положению равнодействующих примыкающих друг к другу тр-ков (1)—(2), (4)—(5), (б) (7). Эти вертикали делят расстояние между линиями центра тяж. смеж. тр-ков в обратном отношении их площадей или пролетов. Следовательно, точки пересечения b₃, с₃, d₃ лежат на «линиях обратных третей» или «сдвинутых опорных вертикалях» (при равных пролетах — просто на опорных вертикалях).

Рассматривая тр-к, образованный тремя первыми сторонами упругого тангенциального мн-ка (на фигура 2 он заштрихован}, можно видеть, что углы его могут перемещаться только по определенным вертикалям, и две стороны проходят через постоянные точки Ау и By. Следовательно, по условию подобия и третья сторона его также должна проходить через постоянную точку J₂, которая лежит на одной прямой с первыми двумя точками. Это соотношение имеет место также для тр-ка, образованного двумя последи ими сторонами веревочного мн-ка, и,следовательно,сторона вый конец балки принимается при этом за точку J 1-го пролета, а правый—за точку К последнего пролета. Точки J и К играют важную роль при расчете балки и называются фокусными. Вертикали, проведенные через фокусные точки, называются фокусными линиями.

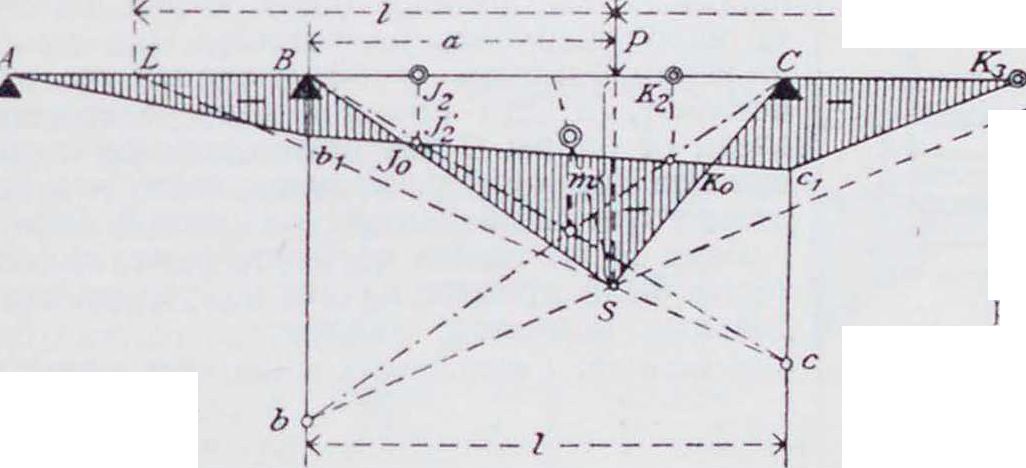
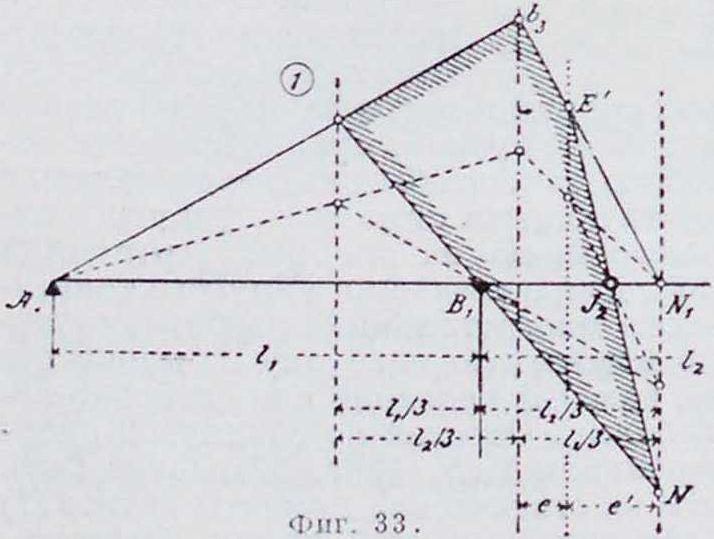
На фигуре 3 показано графическое определение фокусных точек J и К. Прямые ALM и ELM проведены произвольно через точки А и Е. Последующая схема построения понятна из приведенного чертежа. В нижней части фигура 3 дано построение для нахождения как левых, так и правых фокусных точек; они всегда лежат в крайней трети каждого пролета.

3. Определение изгибающих моментов. Когда загружен только один пролет, можно помощью фокусов построить упругий тангенциальный многоугольник, не 4

Фигура 4.

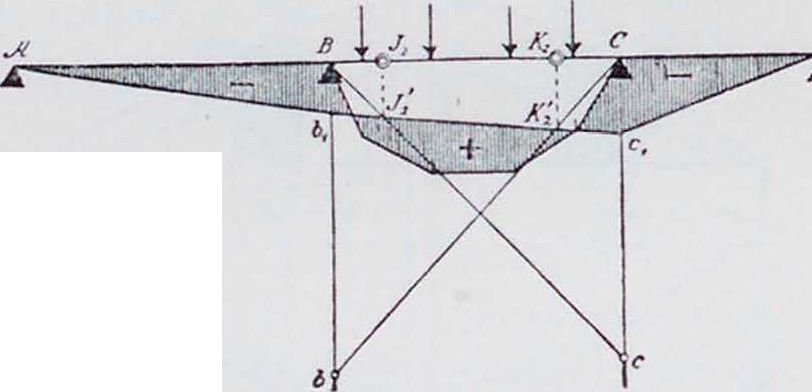
прибегая к построению соответствующего силового многоугольника. Задавшись точкой (3) тангенциального многоугольника (фигура 4) на некоторой высоте на линии центра тяжести эпюры М₀, проводят от нее через фокусные точки стороны веревочного многоугольника по фигура 2. В этом построении отрезки опорных вертикалей B,b_t, b_tb₆ и т. д., умноженные на полюсное расстояние соответствующего силового многоугольника, дают ста-

щади (2) относительно В_х (фигура 2)=·

ur I 3

площади (^относительно С₁он=—|-=

и ^1з Мь в А=& А

в

,так что в.

Mr

C₁c_i — c_tc₅

о (3) отно-а отрезок стат. л.ом. плот. (.3) относит I в стат мом. илощ (3) относит, с Так как точка (3) была выбрана произвольно, то всегда можно начертить веревочный многоугольник так, чтобы отрезок b_tb_tбыл равен моменту площади М,

I²

сительно Βι, деленному на ² c₄c_s—моменту той нее площади относительно С_и деленному на. Тогда отрезки b_iB₁

и с_хС_х непосредственно равны опорным моментам М_ь и М_с. Следовательно, способ построения таков: в выбранном масштабе откладываются отрезки В,b и С_хс, равные статическим моментам площади М₀ отно-

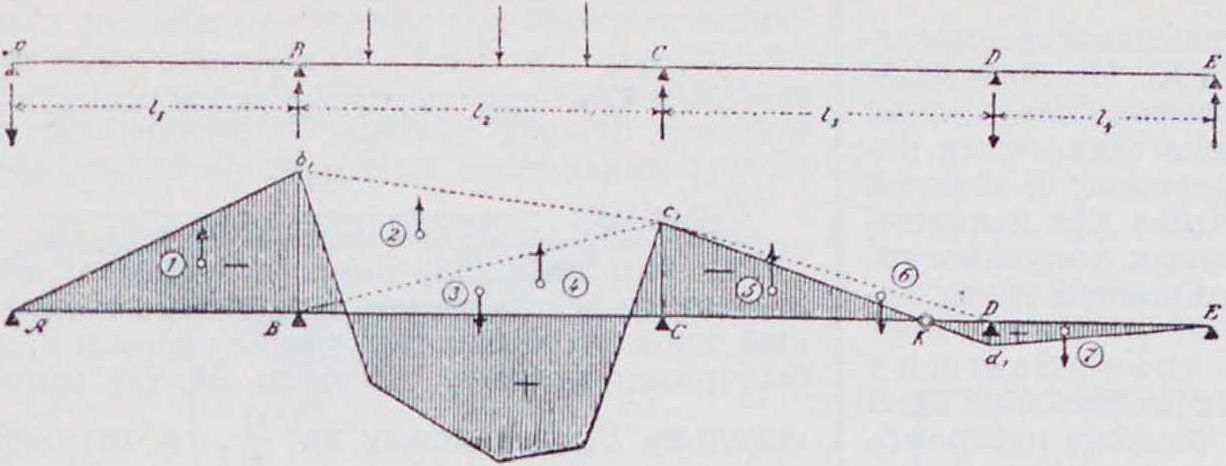
сительно В_х и С_х, деленным на ·-“, проводят перекрещивающиеся линии В_хс и С_ХЬ (показанные в новом положении на фигуре 4 пунктиром) и через точки и К_х пересечения этих линий вертикалями, проходящими через фокусные точки, проводят замыкающую Отрезки, отсекаемые на опор ных вертикалях замыкающей и осью балки, дают опорные моменты М_ь и М_с в том же масштабе, в котором отложены отрезки В_ХЬ и CiC. На фигуре 5 показаны все линии, необходимые для получения по изложенному способу эпюры моментов.

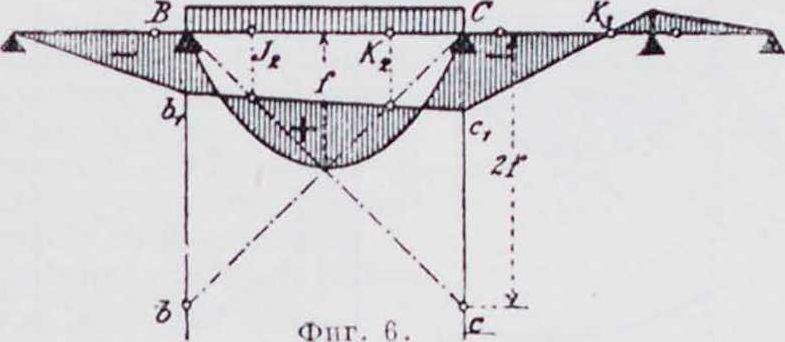
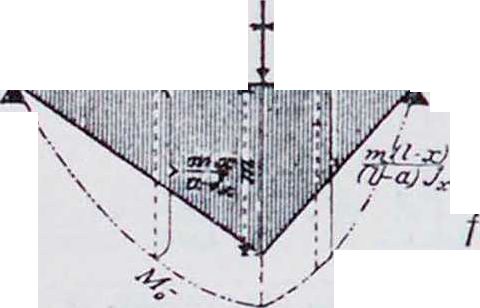
4. В некоторых простейших случаях эти ординаты ВЬ и Сс, откладываемые на опорах, вычисляются весьма просто или находятся графически. Например: а) Д л я случая равномерно распределенной нагрузки д (фигура 6). Эпюра парабола со стре-

площадь ее fl, а момент от-

лой

8

равна

I*

равен g .,. Разделив получаем ВЬ=Сс=2/. Перекрещивающиеся линии, следовательно, проходят через вершину параболы М₀. б) Для случая сосредоточенного груза Р (фигура 7). Площадь М₀—тр-к с вершиной S под грузом Р. Пусть высота тр-ка равна т;

тогда площадь его равна 1т. Расстояние

Фигура 5.

тический момент площадок (2) и (3) относительно В_х. Поэтому можно написать следующие соотношения:

β h — b b ^стат· ^мом плош. (2) относит. Пi

¹ 4 ⁼ 4 6 стат. мом. площ. (3) отио ит. В_х ’ отат. >ом. i лощ. (4) отпо ит. с_х^ ⁴⁼” 4 6 стат. мом. площ. (3) относит. с_х

Известными здесь являются статические моменты площади (3). Статич. момент пло-

центра тяжести от опорной вертикали В== з (ί + я), откуда статическ. момент равен

γ (I + а) и ордината перекрещивающейся прямой па опоре ВЬ =. Также Сс =

щ(Ч-о) ¹

“ (

Эти ординаты можно определить и графически. Влево ивправо от точки приложения груза Р ότι л лдывают отрезки I. Из полученных точек L и Л проводят прямые

LS и RS, которые дают при продолжении в пересечении с опорными вертикалями искомые точки с и b. Перекрещивающиеся линии должны пересечься под центром тяжести треугольника М₀. Если же груз приложен по середине, перекрещивающиеся линчи пересекаются на границе нижней четверти высоты тр-ка М_а. При нескольких грузах

ординаты получаются как сумма ординат, найденных для каждого груза.

5. Предельные значения изгп-б а ю щ их моментов при р а в н о-мерно распределенной п о д в иж-ной нагрузке р. Из эпюры моментов (фигура 7) для одного груза Р видно, что в загруженном пролете всегда есть две точки ·/„ и Ко, момент которых от одного груза Р равен нулю: это так называемые точки перегиба». Когда груз Р движется по направлению от И 1с С, то точка ·/„ движется от I! к J, а точка К₀—от К к С. Отсюда следует, что в пределах среднего участка J К всякое загружение данного пролета вызывает только положительные моменты; поэтому

По этим схемам имеем:

в случае нагрузки I наиб, -у М на внутр. участках

1 и з пролетов и наиб. - М на тех же участках 2 и 4 пролетов

»	»	ft	2	>*	-f V	BO	2 и 4 пролетах
				»	- M	В 1	и з пролетах
*	»	»	3		- M	на	опоре В
*	*	»	i		+ .V	»	» В
»	ft	ft	5	»	- M	»	» с
»	»	ft	6	*	+ M	»	* С

Эпюру моментов для любого из этих случаев нагрузки можно получить, если по 3 2 3 4

ιιι!Ι1Ι!ΐ;ΐ1ΙΙίΙΙΙ:1Ι1Ι1Ιί:

Фпг. 7.

для получения наибольших моментов на этом участке надо данный пролет загрузить полностью, а остальные пролеты загружать через один, так как загружение смежных Пролетов вызовет на этом участке отрицательные моменты, загружение вторых вызовет положительные моменты, и т. д. Противоположная нагрузка вызовет на этом участке наибольшие отрицательные моменты. Показанная на фигуре 8 нагрузка вызывает:

I

II

Для

f -f М на внутр. участке l и з прол.

I — М ь » » 2*4 »

J -f М » ь » 2*4 »

I - м * * » 1»з»

нахождешιя наиоолыиих моменте>в надо загружать оба прилегающйе к опоре пролета, что непосредственно видно из рассмотренных выше эпюр моментов (фигура δ и 7), остальные нее загружаются поочередно.

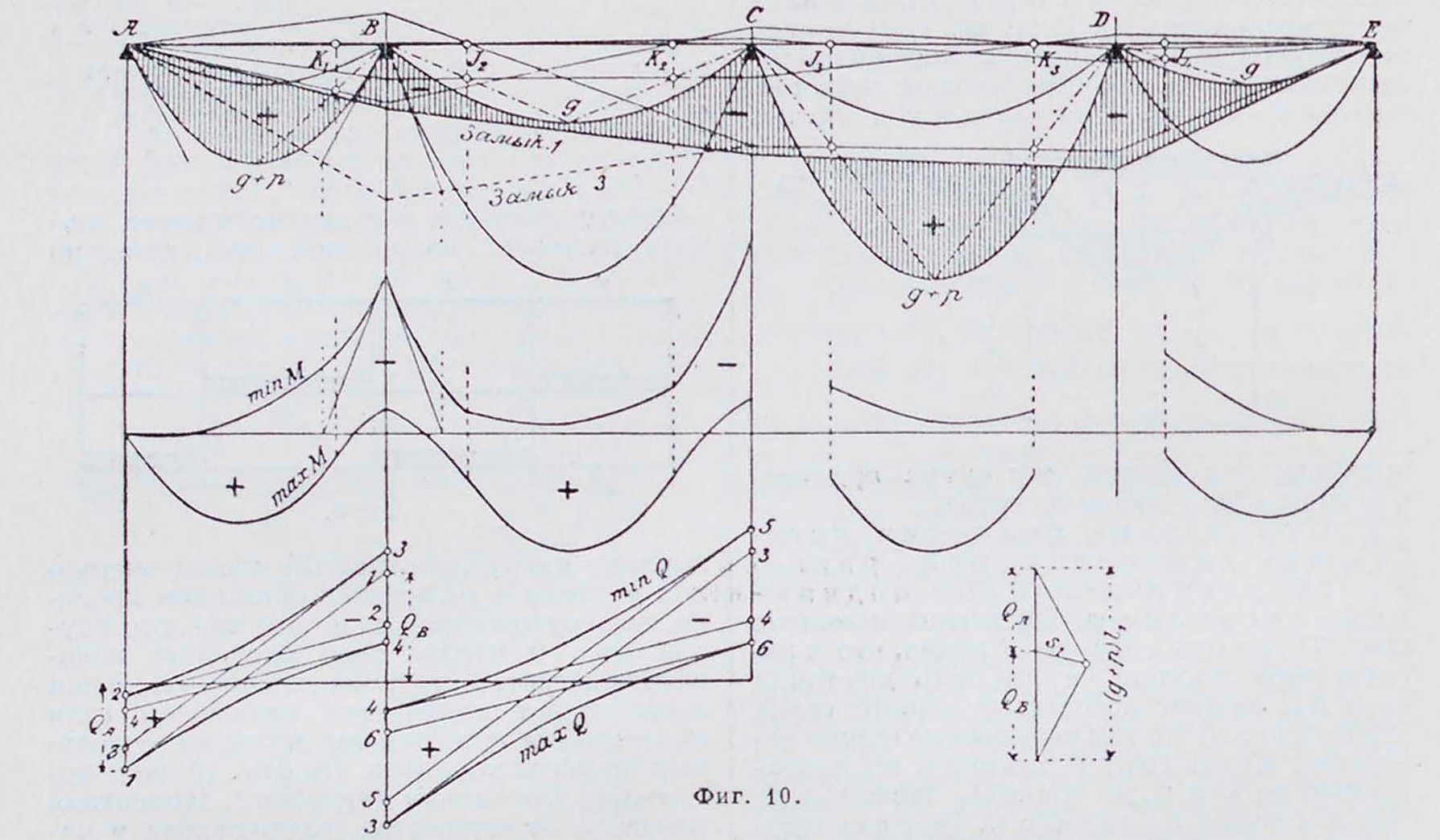
На фигуре 9 даны разные схемы нагрузок: для 4-пролетной симметричной балки при постоянной нагрузке д и подвижной р. иг. 8.

порядку нагружать каждый пролет нагрузкой д или (д + р), оставив остальные пролеты незагруженными, то есть для каждого случая фигура 9 четыре раза проделать показанное на фигуре 6 построение. Окончательная замыкающая получается сложением (или вычитанием) при помощи циркуля отдельных опорных моментов. На фигуре 10 дано построение для случая нагрузки 7. Моментная площадь, ограниченная замыкающей и параболами от полной нагрузки (д р) и одной постоянной д, заштрихована. Отсюда получаем нужные части кривых предельных

(наибольших и

ι-------* <£, наименьших)

^ПтШШттттггт^ моментов, кото-, - Я а. рые отложены на средней части фигура 10. Вследствие симметрии обе кривые годятся также и для симметричных участков: следовательно, нет надобности избирать особо случай нагрузки 2. Из случаев нагрузки 3—б получаем над опорами по две точки предельных моментов и соединяем их кривой с кривыми предельных моментов. построенными для между-фокусных расстояний. Для^ облегчения построения кривых на этих участках можно еще провести касательные в вершинах;

в

Фигура 9.

точка пересечения этих касательных с горизонтальной осью лежит как раз под точкой пересечения касательной к параболе М₀ в ее начале и замыкающей, найденной для данного случая нагрузки. В крайних пролетах построенные кривые плавно проходят через фокусные линии, а в промежуточных—имеют некоторый излом.

7. Э. m. II.

6. II р е д е л ь н ы е значения поперечных сил д л si равномерно распределенной подвижной незагруженный пролет—к загруженной части того пролета, в котором находится рассматриваемое сечение (фигура 11). При при-

"л/Л

!Г!
Λ 4	i! iff
	-МУ

нагрузки ρ. Знак поперечной силы легко определить по эпюре моментов: в каждом сечении балки знак поперечной силы положителен, когда изгибающий момент

Фигура 11.

возрастает, и отрицателен, когда момент убывает (если рассматривать сечения слева направо). Из эпюр моментов, построенных для движущегося сосредоточенного груза, можно заключить, что для получения в сечении ά наибольших положительных попе

речных сил нужно в данном пролете балки загрузить часть, лежащую справа от сечения, оставив левую часть пролета незагруженной. Остальные пролеты надо загружать поочередно таким обр., чтобы загруженный пролет примыкал к незагруженной части, а ближении сечения S к опоре В частичная нагрузка переходит в полную, следовательно, для сечения непосредственно справа от опоры В оба примыкающих к ней пролета надо загрузить полностью. При приближении У к опоре С нагруженный участок исчезает, и для сечения не посредствен но слева от опоры С оба примыкающие к ней пролета остаются незагруженными, что соответствует наибольшей поперечной силе.

Вз51в те же схемы нагрузок (фигура 9), которые были применены для получения предельных моментов, найдем: в случае нагр. i наиб, полок, п >пер. силу при А

Р	Р	»	2	Р	ОТ риц.	»	р при Λ
Р	Р	»	3	Р	Р	»	р слона т В
ь	ь	Р	3	Р	ПОЛ Ж.	»	р справа от В
Р	Р	»	4	Р	»	Р	р слепа т В
Р	ь	»	4	Р	отриц.	ь	» сир на т Р
Р	Р	»	5	Р	»	Р	р слова от С
Р	»	»	5	Р	по лож.	Р	ь справа тС
Р	»	»	6	Р	Р	Р	р слона т С
Р	»	»	6	Р	отриц.	Р	р справа от С
	Для	построения			линий		наибольших и

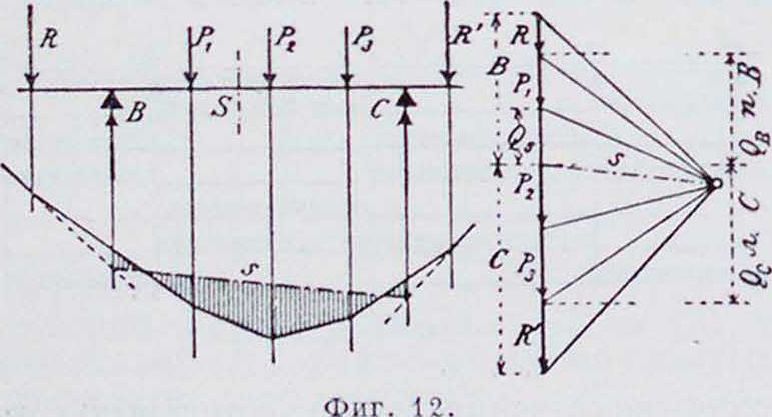
наименьших поперечных сил сначала проводим прямые линии через точки, соответствующие в 1-м пролете нагрузкам от 1 до 4, а во 2-м пролете—нагрузкам от 3 до 6. Кривые предельных поперечных сил должны пойти от точки 1 к точке 4 и, соответственно, от точки 2 к точке 3. Прямые 1—1, 4—4 и т. д. являются касательными к искомым кривым, которые могут быть вычерчены с достаточной точностью как пологие параболы, хотя принадлежат к кривым более высокого порядка. Поперечные силы в загруженном пролете м. б. определены, как в балке на двух опорах с консолями. На фигуре 12 К и К представляют равнодействующие всех сил, включая опорные реакции, слева от В и справа от С. Опорные реакции В н С

получим из многоугольника сил, проведя луч s параллельно замыкающей. В том же силовом многоугольнике отрезок между лучом s и ближайшим слева от сечения грузом дает поперечную силу Q,=В — R-1.

Таким образом величины R и R определять не приходится, если только известно положение замыкающей, зависящее от опорных моментов. Силовой многоугольник, соответствующий параболе (д+р), вычерчен на фигуре 10. Луч s_tмногоугольника параллелен замыкающей 7.

Верхпий отрезок равен <У_Л, нижний—Q_B.

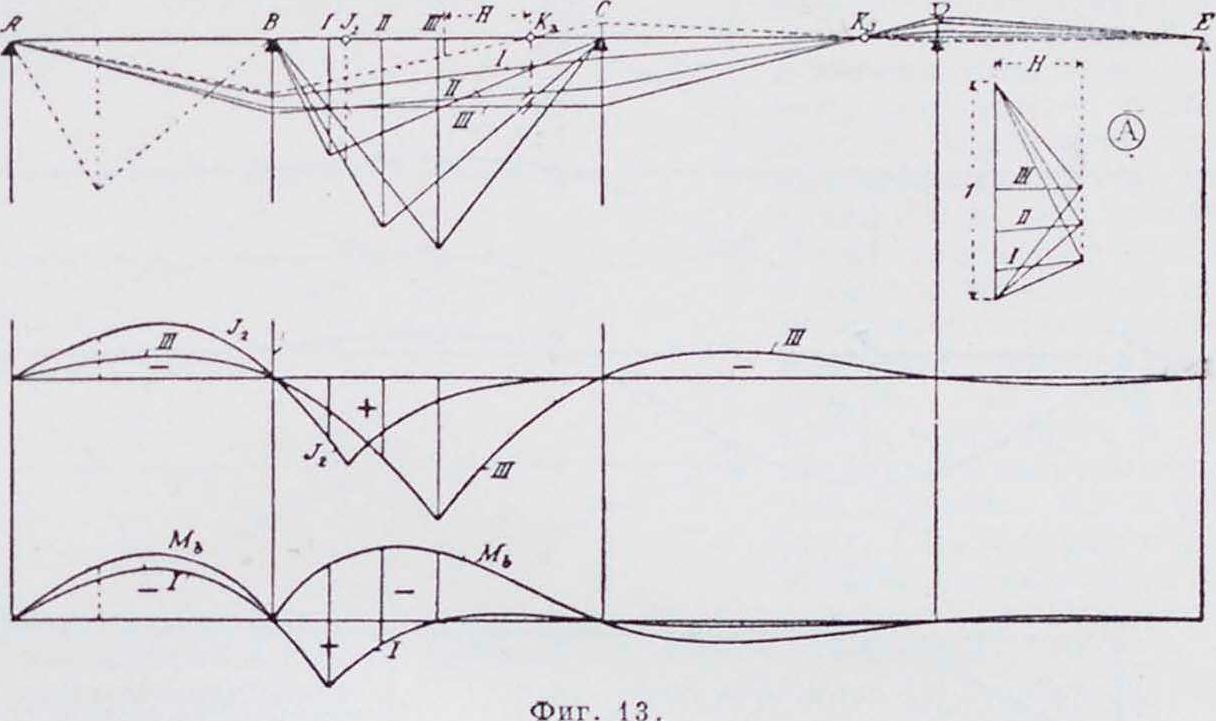
7. Линии влияния моментов и поперечных сил (фигура 13 и 14) требуются при расчете В. н. на действие сосредоточенных подвижных грузов (давление колес). Линии влияния моментов можно получить из нескольких эпюр моментов, составленных для одного груза Р= 1, приложенного в ряде точек. Каждая эпюра дает ординаты для всех линий влияния под точкой приложения груза Р. Все построение линии влияния заключается только в перестановке ординат (фигура 13). Линии влияния поперечных сил в пролете, где взято сечение, строятся из силовых многоугольников, соответствующих тр-кам М₀ (фигура 13, А). Для всех положений груза длина линии сил остается= 1.

Лучи, проведенные в этих мн-ках параллельно соответствующим замыкающим, делят линию сил на две части.

Верхний отрезок дает поперечную силу в сечении, когда груз Р=1 находится справа от сечения; нижний отрезок равен поперечной силе, когда груз приложен слева от сечения. Эти отрезки служат ординатами линии влияния поперечных сил. Отсюда видно, что линия влияния поперечных сил должна состоять из двух ветвей с уступом против сечения, равным единице (фигура 14). Верхняя ветвь находится слева отсечения, нижняя—справа. Верхняя ветвь получена из нижних отрезков, а нижняя—из верхних отрезков силового многоугольника. Линин влияния поперечных сил для любого сечения, находящегося в незагруженном пролете, получается при рассмотрении этого пролета как простой балки с консолями. Внешние силы (и опорные реакции) слева и справа дают равнодействующие R и R на консолях. На фигуре 15 показано определение опорных реакций И и С при помощи силового мн-ка и замыкающей. Определять R и R не требуется, т. к. Q=B—R определяется из прямоугольного тр-ка, у которого одни катет равен Н, а гипотенуза парал лельна заранее найденной замыкающей или линии моментов. Знак поперечной силы положителен при возрастании моментов слева направо и отрицателен при убывании. Таблицы Винклера непосредственно дают предельные значения моментов и поперечных сил в симметричных балках до 4 пролетов при постоянной и подвижной нагрузках. В таблицах Griot даны ординаты ли

нии влияния, включая некоторые случаи неравных пролетов.

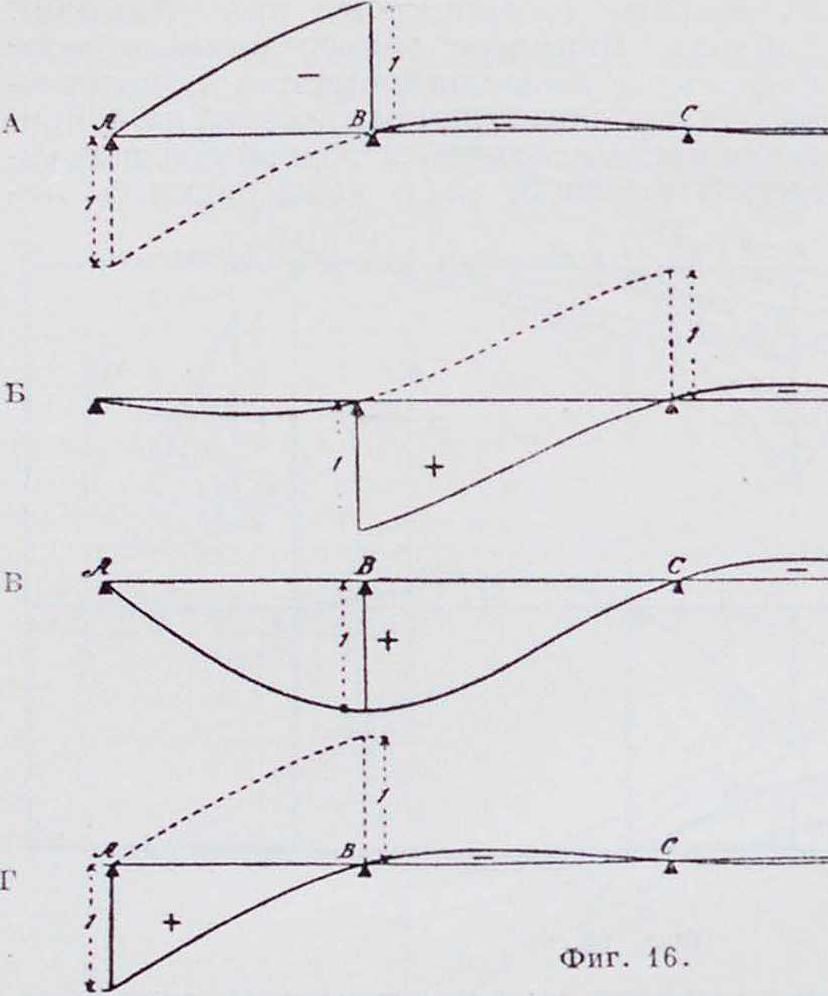
8. Линия в л и я н и я опорных ре-а к ц и й. Если Q_r—поперечная сила непосредственно справа от опоры В, а — _г> слева, то .можно напи сать; Q_r= Qi+B, откуда B=Q_r—Q_l. Таким обр. опорную реакцию для

Фигура 14.

любого положения груза, а следовательно и линию влияния ее, по-лучим как разность (вернее—сумму, т. к. знаки противоположны) между поперечными силами справа и слева от опоры. На фигуре 16, А и Б показаны линии влияния поперечных сил слева и справа от опоры В, и по ним построены линии влияния опорного давления В п А (С и D).

Фигура 15.

Линия влияния опорной реакции имеет фор-му упругой линии балки при замене опоры действием внешней силы.

9. Балки с защемленными ко п-ц а м и. Вместо защемления можно пред-

ставить на конце балки две очень близких одна от другой опоры, то есть вообразить, что к крайнему пролету примыкает еще один

бесконечно малый пролет ί„. Как видно из фигура 17, с уменьшением пролета 1₀ фокус Jj приближается к трети пролета 1_г. Зная точ

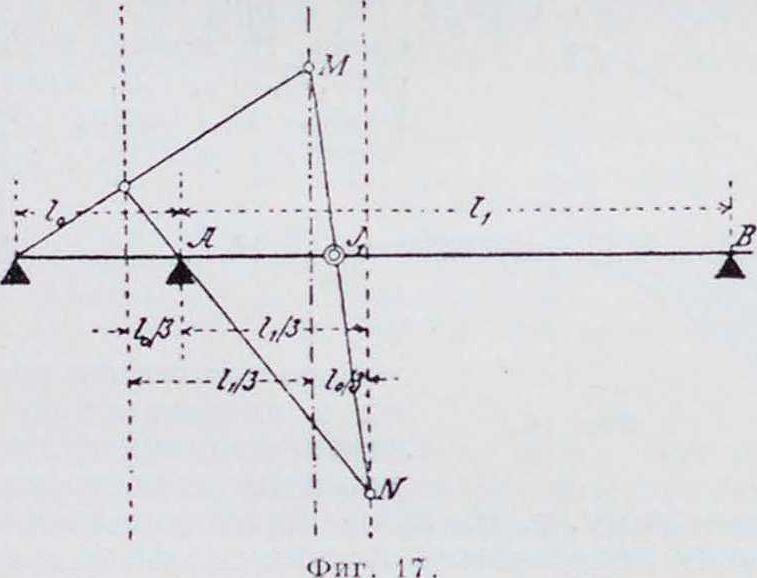
ку Ji, по предыдущему находим фокусы, моменты, поперечные силы и прочие: фокус ./,

пая балка с одним или двумя защемленными концами м. б. решена, как неразрезная, если защемление заменить присоединением бесконечно малых крайних пролетов.

II. Свободно лежащая Б. н. с переменным моментом инерции 1_Х.

Эпюр а м о м е н-т о в этом случае также строится из эпюр М₀ и замыкающей, заданной опорными моментами. Упругая линия,как и при постоянном моменте инерции, находится при помощи упругого тангенциального многоугольника, с той только разницей, что вместо простой мо-ментной площади нужно взять так называемую «приведенную моментнуюпло-

Му Му щадь:. заменяя ее площадью ~ при по-

^Ά *Х ¹Х

стопином Е или площадью М, ·, где

1_т—средний в балке момент инерции.

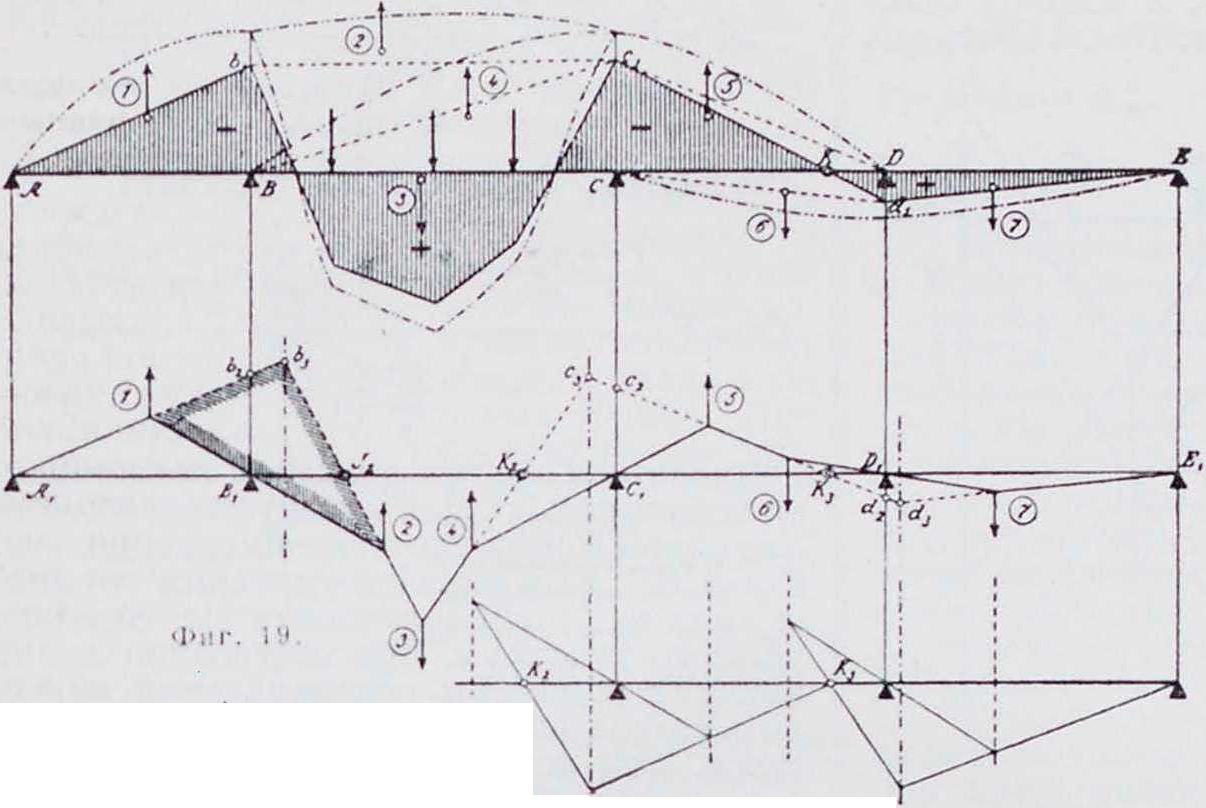
Пусть в балке на фигуре 19 загружен только второй пролет. Для построения упругого тангенциального многоугольника приведенную моментную площадь разбиваем на7 площадок, из которых известна только приведенная площадь (3), полученная из известной эпюры М„. Остальные площадки получаются из треугольников и зависят от опорных моментов. В этом случае центры тяжести не лежат на расстоянии у, от опор и их не надо определять особо как центры тяжести приведенных многоугольников. Положение их, как и в простых треугольниках, не зависит от высоты треугольников, то есть от опорных моментов, а потому для определения центра тяжести приведенных треугольников можно высоту треугольников принять равной 1.

По фигура 20 расстояние d_n линии центра тяжести от вершины треугольника:

ГI .х х - (1х Гх х fix

‘ /у .1 Ту

i i х dx Γχ dx

.1 I I у .1 ly

Разделив балку на несколько участков s конечной длины и обозначив полученное вместо

dx s

отношение х 1 j

* х через

*х через w, а выражение от-

. Σχ · U’t

получим d„=- _Σ~,

играет при этом такую же роль, как про- куда следует, что равнодействующая ц. т. межуточные фокусы (фигура 18). Однопролет- приведенных треугольников совпадает с

Так кате статический момент площади приведенного треугольника (2) относитель-

j.

но В равен М_ь f ¹~~х, то равнодействующей «упругих грузов» w_x, приложенных по середине участков s. Точки пересечении Ь₃, с₃, d₃ первой и третьей,

Такое же отношение имеют в эпюре моментов отрезки Сс_г и Ddj, следовательно, полозкение точки пересечения К₃, то есть фокусной точки, сохраняется в третьем пролете при отсутствии на нем нагрузки. То же можно доказать и для фокусных точек K_t,J₂ и т. д. остальных пролетов. Так.обр. в каждом пролете Б. н. с переменным моментом инерции, как и балки с постоянным моментом инерции, имеется по две точки J и К, которые зависят только от длины пролетов и размеров поперечного сечения балки и обладают теми же свойствами, как фокусные точки в пролетах с постоянным моментом инерции. Отрезки Bjb_t и b_tb₅(фигура 23), которые образованы упругим тангенциальным многоугольником на опорных вертикалях, имеют отношение:

В]Ь₄ стат. мом. площ. (2) относит. В

b_tb₃ стат. мом. площ. (2) относит. В

	WJtr	Lr

-JC---djT

.<-·—:

Λ-

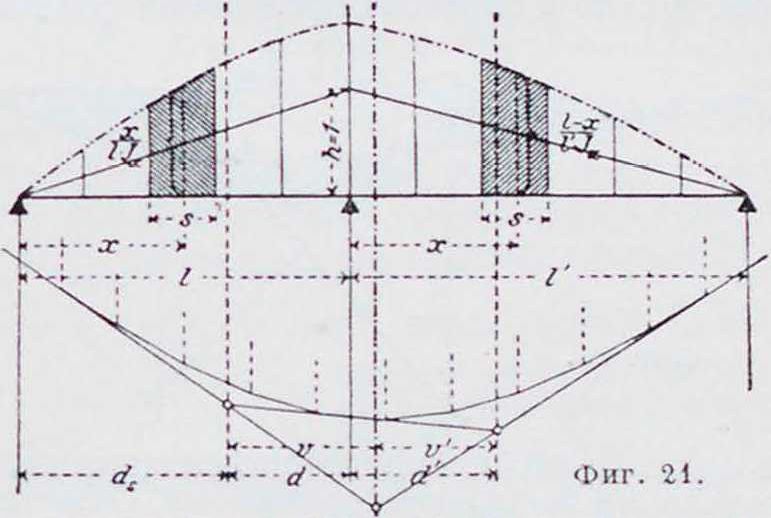
четвертой и [ шестой, шестой и восьмой сторон упругого тангенциального многоугольника на фигуре 19 лежат на линиях центров тяжестей площадей смежн. приведенных треугольников (/) и (2), (4) и (5), (6) и (7). Ц. т. для одной и для двух смежных площадей можно найти, разделив приведенную площадь на вертикальные полоски и построив, как показано на фигуре 21. общий веревочный мн-к. Расстояние ν «сдвинутой опорной вертикали» (вертикали, проходящей через ц. т. двух смежных приведенных тр-ков) от ц. т. левого приведенного тр-ка можно вычислить по формуле:

У, " Г

г Li ¹ -*

ν =

l

¹ V

Г

где d=ί - d_s; Щ’__х=~(Г-х) и и»=* х.

¹х * X

Третья, четвертая и шестая стороны упругого тангенциального мн-ка (фигура 19) проходят через постоянные точки, то есть фокусные точки </₂, А₂, К₃, не зависящие от величины опорных моментов. Эти точки находим чисто геометрически, после построения сдвинутых опорных вертикалей и линий центров тяжестей приведенных тр-ков.Положение фокусных точек определяется так же, как в случае балки с постоянным 1_Х. Отрезки С^с., и П,</₂ должны относиться, как статические моменты приведенных площадей (у) и (С) относительно и D, (фигура 22), то есть

/Го ч dx

^х) · т

M_h

стат. мом. площ. (3) относит. В

Для определения опорного момента поступают так же, как в случае балок с постоянным моментом инерции, а именно: от-кладывают на опор- Ί Д, ных вертикалях ординаты BJ) и C₁C, равные статическо-

—&

Фигура 22.

му моменту приведенной площади М₀ относительно В и С, деленные на интеграл

С,с₂

Mr

Ιχ

I -х х dx

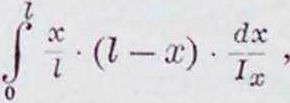
U, d«

ΓΜ,ι x

.1 Ιχ I о

(l-x) dx

н проводят перекрещивающиеся прямые В_хв и C_tb, пересекающие фокусные вертикали в точках J и К[. Далее, проведя через точки Jj и К замыкающую, получают на опорных вертикалях отрезки, равные искомым опорным моментам.Этиотрезки измеряются в том же масштабе, в котором отложены ординаты B_l b и С,с. После этого вся

Фигура 23.

эпюра моментов легко строится по фокусным точкам (фигура 24). Итак, расчет балки с переменным моментом инерции отличается от расчета балки с постоянным моментом инерции только в способе определения фокусов

Таким образом ордината

Bb=Р

2? ·(«-*>

Аналогично определяется ордината а I

Сс=Р

ν⁰-“. *

jU (

Фигура 24.

и ординат перекрещивающихся прямых, в остальном же расчеты одинаковы. Отметим, что в балках с симметричными изменениями моментов

.®.t-#--·* инерции орднна-

^ > ты перекрещива ющихся прямых ВЬ и Сс равны удвоенной стреле=--- параболы

М„, как и при постоянном моменте инерции, и находятся проведением перекрещивающихся прямых через вершину параболы.

При действии сосредоточенного груза Р момент приведенного треугольника М₀ относительно В (фигура 25) равен:

Фигура 25.

/т dx, Г т , _s „

α^Χχ·Τ_χ+]ΓΤα·(¹-^χ)·^χ·

О а

dx

I*

Вставив сюда Р -а - (1-а)

вместо т его значение т =

получим:

{¹ -,-2«.·* + $ 2 ^ад*^-х^1_*)}

•о /i ‘

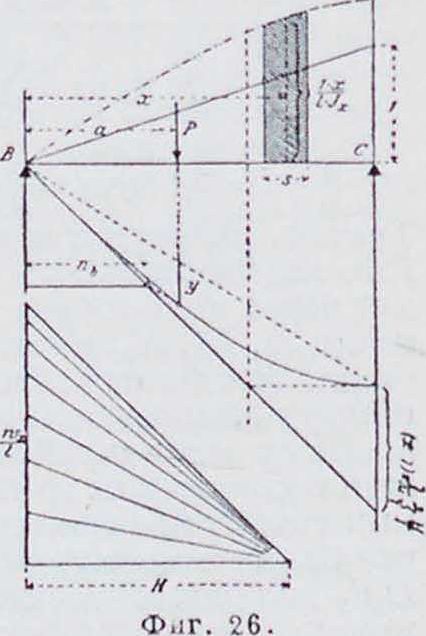
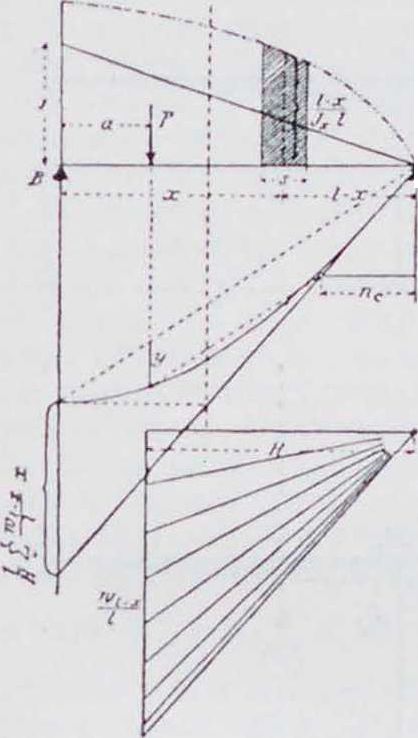
Числители обоих выражений представляют собою изгибающий момент нарасстоянии а от опоры в свободно опертой однопролетн. балке ВС, нагруженной упругими грузами w_x или v;i___x, приложенными по середине каждого участка s. При построении линии влияния моментов рекомендуется вычислить изгибающие моменты на границах участков. Эти моменты дадут величину числителя в выражении для ординат перекрещивающихся прямых при положениях груза Р — 1 над границами участков s. Остается только разделить их на знаменатель, не зависящий от положения груза. Графический способ получения ординат Bb — n_h Р и Сс-^)1_С Р показан па фигура

26 и 27. Для получения ^k наибольших значений моментов и поперечных силотравномерно распределенной подвижной нагрузки р располагают последнюю по пролетам так же, как в случае балки с постоянным моментом инерции (фигура 9 и 11). Построение линий влияния производится по методам, приведенным выше для балок с постоянным аксиальным моментом инерции пеперечного сечения 1_Х.

Если момент инерции, оставаясь постоянным внутри каждого пролета, изменяется при переходе от одного пролета к другому, то приведенные тр-ки остаются геометрия, треугольниками, и ц. т. их лежат в третях пролетов. Смещенные опорные вертикали лежат на линии центров тяжести пары смежных приведенных треугольников.

Ординаты перекрещивающихся прямых находятся, как и при постоянном моменте инерции.

Если концы балки с переменным моментом инерций будут защемлены, то ее можно рассчитать, как это было указано для балок с постоянным моментом инерции, предположив по концам две весьма близкие опоры. Отличие в расчете будет заключаться в том, что фокусная точка будет определяться как центр тяжести приведенного треугольника.

ill. Б. н., упруго защемленная на опорах, с постоянным моментом инерции.

В отличие от рассмотренного типа балок, свободно лежащих на опорах, то есть поворачивающихся на опорах независимо от последних, часто встречаются, в особенности при железобетонных сооружениях, балки неразрезные, жестко связанные с опорными стойками. В указанном случае опорные стойки вместе с бй изгибаются от нагрузки и тем самым оказывают упругое сопротивление ^поворотубалки в узловых точках. При расчете можно пренебречь влиянием удлинений от осевых с и л; то гд а э п ю р а моментов опять получается из свойств упругого тангенци-альн. мн-ка. В случае, когда одна из опор неподвижно закреплена или же когда вся система и нагрузка на ней симметрично расположены, балка при деформации не перемещается в горизонтальном направлении, и узловые точки остаются неподвижными. Если же нет ни симметрии ни неподвижной опоры, узловые точки получают нек-рое смещение. При расчете допускают вначале, что балка неподвижна, затем вводят поправки, учитывающие влияние смещения. Часто, впрочем, поправками от смещения пренебрегают.

Фигура 27.

роне стойки). Если стойка имеет шарнир внизу, эпюра моментов в ней—тр-к (фигура 30), и угол поворота (девиация) τ в голове стойки получается как опорное давление балки от фиктивной нагрузки площадью · Из

1 h 2

. Μ, ; h получается уравнения EI, τ=Μ. ГрГ ’ Если же стойка внизу за-

at. 1₈

щемлена, момент М, вызывает в ней такие же изгибающие моменты, как в балке с одним защемленным концом и другим, в котором прило- _м

жен момент М„

свободно опертым (фигура 31). Линия *

моментов должна пройти через фокус, к-рый находится на расстоянии одной трети высоты от защемленного конца. Отсюда, момент в защемлен- _{фиг 30}. ном конце равен 1

Фигура з 1.

ном е.

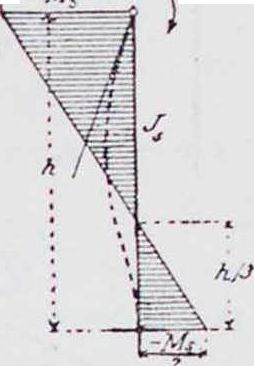
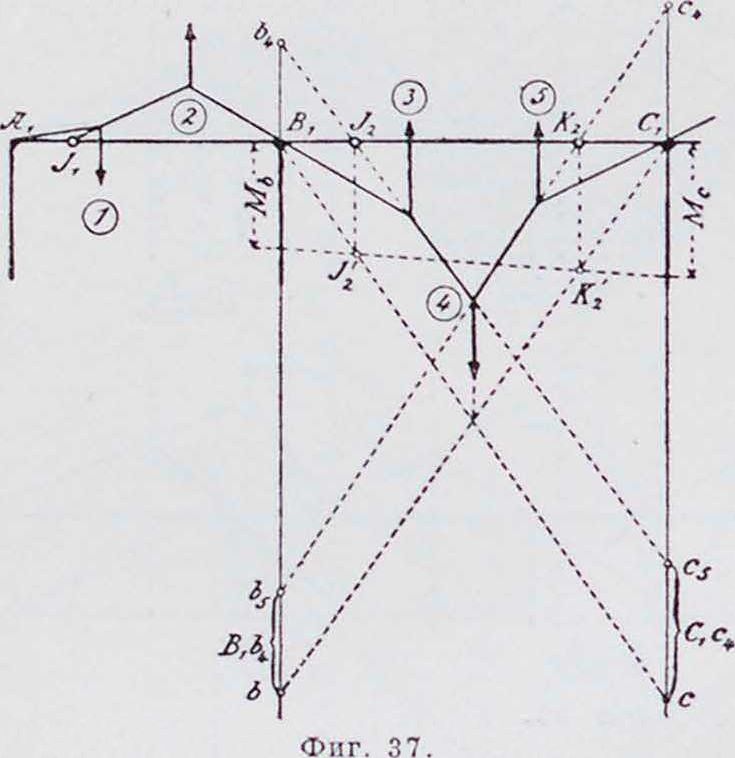
На фигуре 28 показана эпюра моментов при загрузке второго пролета. Изгибающие моменты в балках и стойках отложены с той стороны, на которой возникают растягивающие напряжения. При переходе через стойку моменты в балке уменьшаются скачками, уступами. Уступ равен как раз той части момента, которая передается на голову стойки. Это следует из условия равновесия вырезанного узла. На фигуре 29 изображены моменты, действующие в узле В, причем направление их совпадает с тем, к-рое в дальнейшем считается положительным. Из условия равновесия вырезанного узла М_ь — М, — М_ь — 0,

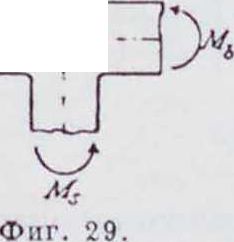
откуда М,= Мь — М_ь. В узле С получится, наоборот: М,= М_е—Мс (положительный момент М, дает растяжение на левой сто-

Угол поворота головы стопки равен сумме элементарных углов поворота τ в сечениях от защемленного конца до головы стойки, то есть или В общем виде т= Μ,ε„ где ε,

означает угол поворота, вызванный моментом М=1. В стойках с шарнирным концом

_£=^h в стойках же с защемленным кон-⁸ з EI_S

этих выражениях I, обозначает момент инерции стойки при изгибе в плоскости системы. и. i ii Прогиб балки на опо рах равен нулю; следовательно, построив вере во ч н ы и м но гоу гол ьни к (упругий, тангенциаль-ный мн-к) для балки АЕ как лежащей на двух крайних опорах и нагруженной фиктивной моментной нагрузкой, нужно провести замыкающую так, чтобы она перес.екалась с соответствующими сторонами упругого касательного мн-ка на опорных вертикалях (фигура 32). Для построения упругого тангенциального многоугольника разбиваем фиктивную моментную нагрузку на площадки так же, как было сделано для свободно лежащей балки. Отрезки на сдвинутой опорной вертикали у В, (фигура 32) могут быть приняты за статические моменты грузов (2) и (2) относительно этой линии. Поэтому, обозначив через II полюсное расстояние силового мн-ка, относящегося ко второму веревочному многоугольнику, получим:

, , i Му г, г. Myh-it

н

Mbh

3 6 я

h _ м_ъ-1_х-

3 6 н

Так. обр. b₃bз=b„b₃ - bji₃=‘eJ* (М_ь - Μ’,) =

ίι h _Μ h- Ii T_

6Я ^s вн " * с_Ь

Кроме того, угол т может быть выражен через угол наклона второй стороны упругого изменится. По вершины углов должны оставаться на тех же вертикалях, а три стороны должны проходить через одни и те же постоянные точки А_х, В_и N_x. Из подобия следует, что и четвертая сторона будет проходить через некоторую постоянную точку

тангенциального мн-ка (фигура 32), а именно:

tgxNfrN-Щ tgr-

Отсюда отношение отрезков h h г. ei

b₃Ь₃: NN_X =

то есть величина постоянная, не зависящая от нагрузки второго пролета балки. Точка Е пересечения обеих прямых b₃N_x и b₃N, как

J₂ на оси А₁В₁. Точку эту, независимо от вида нагружения, можно найти графически, как показано на фигуре 33; построение начинается с проведения произвольной прямой, проходящей через точку А, и продолжающейся до пересечения со сдвинутой опорной вертикалью Ь₃; дальнейший ход построения понятен из чертежа. Аналогичная связь существует для сторон 5—6—7—Е веревочного мн-ка. Для тр-ков (6) и (7) можно написать такие же выражения, которые были написаны для тр-ков (I) и (2). Так же нахо-

СЧ1Г. 34.

видно из написанных равенств, должна лежать на вертикали, делящей расстояние между сдвинутой опори, вертикалью и точкой N_x на расстоянии */₃ пролета в отношении

= ,}1гт_ь, ^гД^е I момент инерции балки.

При какой-либо другой нагрузке во втором пролете форма четыреугольиика (1) b₃EN

дится и фокус К₂ второго пролета. По фигура 34 отношение отрезков

С_хс_г _ стат. момент груза (Д) относит. С_х _ и_х<1_г ~ стат. момент груза (в) относит. D_x ~

Щ1₃ h

2 3 _ М

Μ ,ί I а 1₃ Мл

2 3

откуда следует, что фокусная точка 1<₃совпадает с нулевой точкой ненагруженно-го третьего пролета. По тому лее способу молено найти точки в ненагруженных пролетах, лежащих слева от нагруженного. Значение фокусов J и К такое же, как в Б. н., свободно лежащей на опорах.

11а фигура 35 дано все построение для определения положений фокусных точек. Если крайние опоры шарнирные, то левую опорную точку принимают за фокус ·/, а правую—за фокус К. Характер стоек,т.е. имеют ли они внизу защемление или шарнир, отражается только на соответствующей величине e_s. Если одна из стоек не жестко связана с бй, то e_s=ос, так как i,=0 (нет упругого противодействия),

а также ^е,=0, то есть вер-

Так как в упругом тангенциальном мн-ке Λ₃Ν есть касательная к упругой линии в точке А_г, то tg ^ιλ^τιΛ_ιΝ =

i,.. i

κι

я

tK t=

El

. vv=:; ι^Λγι,.ν-:, · ^hu ·τ

t	1 г -ч	• jS 1	, 1 : I 1
1 1	1 ! ! _!_Ai—_1__Ь,	к · г ΐ γ.	! v4 1 W 1 ^ V r
	ЧА; i i	!
г-S-	-ЧН г"-*-н	·», Γ τ	УЧ!
	И-Н Ч-ЧЧ	-U. J L6.i Г J 1 1 J i	-H

r l,

?^яш_л

и

2£Ji_k

r 2£J,

e Z£Ji_d

V- e e -*! ! W • 1 i j/rvJ ! /f,		i f Г ; i yS i · /.
	1 · ifl i i L 1 1 Г i 1 ·	1	К · ! 1	1 1 1 1

r~2£Jl_c

Фигура 35.

e t>

тикаль, проходящая через E (фигура 32 и 33), совпадает со сдвинутой опорной вертикалью. Н случае полного защемления какого-либо конца балки ближайший фокус находится в трети пролета, что следует из тех лее сообралсе-ний, которые были приведены для обыкновенной неразрезной балки. После того как найден крайний фокус, дальнейшее построение ведется по фигура 35. Если концы балки в точках А и Е жестко связаны с крайними стойками, то и в этих точках

появятся опорные моменты, и эпюра моментов в ненагруженном первом пролете будет иметь вид, показанный на фигуре 36. Отрезок h,а, умноженный на Ы, дает статический момент площади (ί) относительно A_lt так что

4,в.= я · М

1

я

Отсюда отношение Α^ι^-.ΝΝ,=.1 ,-_7₁:•7₁А^Г1=

= e : e =

или е : с

EI

Я

-ΕΙα

Т. о. вторая сторона упругого тангенциального многоугольника должна пройти через фокус Jj, делящий [ в отношении е:е.

Отношение отрезков:

Аχα,-.ΒΑ-^:=М_п : M’,

то есть точка совпадает с нулевой точкой момента в ненагруженном первом пролете.

Определение моменто в п р и н а-грузке только одного пролета. После определения фокусных точек можно найти опорные моменты точно так же, как в обыкновенной Б. н. с постоянным моментом инерции. Продолжив средние стороны веревочного мн-ка (фигура 37) до пересечения с опорными вертикалями, получаем те Hie отношения для нахождения ординат перекрещивающихся линий под опорами, как на фигуре 4. Поэтому построение ординат перекрещивающихся прямых делается но способу, показанному на фигуре 6 и 7. Разница заключается только в ином положе-нии фокусов, которые при упругой заделке ближе к середине пролета. На фигуре 38 показана эпюра моментов в первом пролете балки, нагруженной равномерной нагрузкой и жестко связанной с крайней стойкой.

Переходные коэффициент ы μ дают уменьшение величины моментов при переходе через стойки; при помощи их эпюра моментов продолжается вне нагруженно-го пролета. Числа μ м. б. взяты из построения, сделанного для определения фокусных точек (фигура 32): Ь₀Ь₃=-^Л^-¹* ; Ь₀b_а=^м*д^г* · Разделив эти выражения, получим ί"!’³ =

OqOs

= Если идти вправо от нагруженного пролета, то коэфф. μ надо брать из отно

шений ^сс3=/i и т. д., получаемых при по-

строении точек К. Для каждой опоры получаем два значения μ, смотря по тому, находится ли нагрузка справа или слева от нее.

Аналитическое определение коэффициента μ основано на том, что при переходе справа налево угол поворота τ упругой линии в голове стойки, вызванный М,=М_ь — М_ь. равен отрицательному углу поворота левого пролета под влиянием действующих в этом пролете моментов. Этот последний угол β равен опорной реакции простой балки А В,

нагруженной фиктивной нагрузкой,

так что β=(2М’_Ь — М_а); заменив М_а

из равенства М_а=(фигура 36), получим о h Afь( h — Sii) _γτ

β=_6ΕΙ · _ _2ι). Но так как тот же угол

β=— τ=—М, E_h=— (MI, — М_ь) е_ь, то получаем уравнение

Ц ( 1, - 3i,) д.,

С EWx-ii) ^Ь

^—(-Щ — М_ь) е_ь,

которое и дает искомое—переходный коэффициент

μ

Mi,

Мь

1

Ма/,-3i,)

ΒΕΙ £(,((, -i,)

Вообще для перехода справаналово(фигура39),

Рг =

Mr

М_г ⁼

1

(,·( lr-Sir)

1 +

6EI e,- (l_r - i_r)

а для перехода слева направо Mr t

M_r

Pr-

1 +

6* ♦ I ( 4- I B/i₊ I)

BE I e_r (l_{r +} i — hy + i) Поперечные силы и опорные давления на стойки определяются, как и в свободно лежащей Б. н., при помощи силовых

Mr,

м_г

Mr.,

I

Φ.,Γ.

мн-ков, соответствующих эпюрам моментов. 11о-

неречные силы в ( о·.ф силовых мн-ках находятся црове- _ф„_{г 39}

дением лучей, параллельных замыкающим. В ненагружен-пых пролетах поперечная сила равна катету прямоугольного треугольника, другой катет которого равен полюсному расстоянию Н, а гипотенуза параллельна линии моментов (замыкающей) в данном пролете. При равномерно распределенной подвижной нагрузке р схемы невыгоднейших случаев нагрузки такие же, как и для свободно лежащей балки (фигура 9). Линии влияния моментов и поперечных сил, необходимые при расчете на сосредоточенную подвижную нагрузку (давление колес), получаются из нескольких эпюр моментов для грузов Р=1, как было изложено выше (смотрите фигура 13 и 14). Для каждой промежуточной опоры существуют два опорных момента с разными линиями влияния.

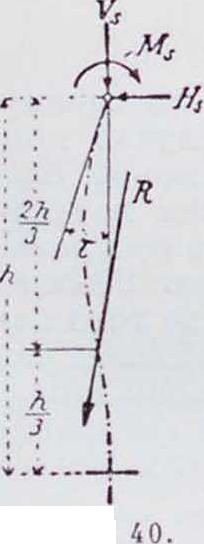
Стойки работают на совместное действие изгиба и осевой силы. Обычно для расчета стоек и фундаментов иод ними достаточно один из примыкающих пролетов загрузить полностью, а остальные—через пролет. Для более точного расчета можно начертить линии влияния ядрового момента в нескольких сечениях стойки и по этим линиям уже вполне точно определить предельные значения напряжений на краях сечения. Линии влияния ядрового момента определяются из величины равнодействующей сил, действующих в стойке при каждом положении груза Р=1. Равнодействующая эта слагается из вертикальной составляющей V, равной сумме (разности) поперечных сил справа и слева, и горизонтальной составляющей II,. При защемленной внизу стойке II, находится из условия, что момент на расстоянии

1 3

высоты снизу равен 0; тогда 11,=· М, -г

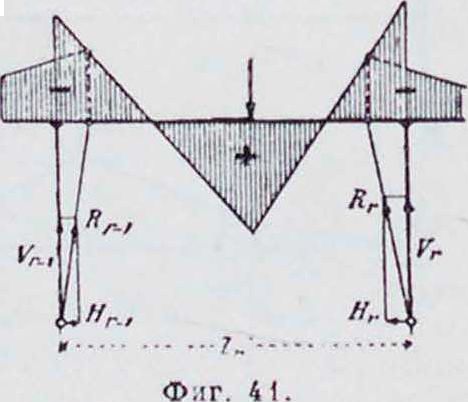
(фигура 40;. Если стойка имеет внизу шарнир, то Н, =, т. к. равнодействующая долж на пройти через шарнир (фигура 41). В обоих случаях равнодействующая пересекает ось балки в точке, лежащей на той вертикали, на которой пересекаются моментные линии примыкающих к данной стойке пролетов

+ Δ

Фнг. 42.

(фигура 41). Разложив на уровне балки равнодействующую R, на горизонтальную и вертикальную составляющие, можно показать, что и в данном случае моментная площадь является непрерывным веревочным многоугольником.

Полученные до сих пор выражения моментов поперечных сил верны только тогда, когда все силы 11 „ (направленные при положительном М, вправо, и наоборот), передающиеся на балку через головы стоек, взаимно уничтожаются или воспринимаются

»7=1, умножить на

ш

Я,

или па

Смещение η -1 балки вправо дает как смещение нижних

какой-либо неподвижной опорой. Если же в результате остается сила Ml и неподвижной опоры нет, то эта невоспринятая сила Ml дает в балке такие дополнительные внутренние усилия, какие получились бы от действия внешней силы Ml (фигура 42). Т. о. все горизонтальные силы, передающиеся на балку через головы стоек, должен быть рассматриваемы как внешние силы. Вызванное ими горизонтальное смещение изменяет все найденные выражения внутренних усилий. Влияние смещения вычисляется следующим образом. Дают балке нек-рое малое горизонтален. смещение вправо,например, »;=1 см, находят возникающую от этого смещения эпюру моментов в балке и стойках и определяют силу Н_г, вызванную сопротивлением стоек смещению и равную сумме всех передающихся на балку через головы стоек горизонтальн. сил,—тогда принятое смещение»7=1 как бы соответствует действию силы Д,. Если действительная сила будет II или MI, то для определения искомых моментов, вызванных действительной силой, надо моменты, полученные

-A f_s ---*<~-»_ул — * Фигура 44.

от смещения я «Г

такие же моменты, концов стоек на ту же величину влево, если балку закрепить неподвижно. Эти моменты можно получить, как сумму отдельных моментов, которые вызваны смещением конца каждой стойки. При смещении конца только одной стойки (фигура 43) линия моментов во всех пролетах пройдет через фокусн. точки, так как исходи, пункт этих моментов находится только в голове данной стойки. Отсюда следует, что для построения эпюры моментов достаточно в данном случае определить два опорных момента над смещенной стойкой. Пользуемся для это го тем условием, что углы поворота упругих линий балки и стойки в данном узле равны между собой.

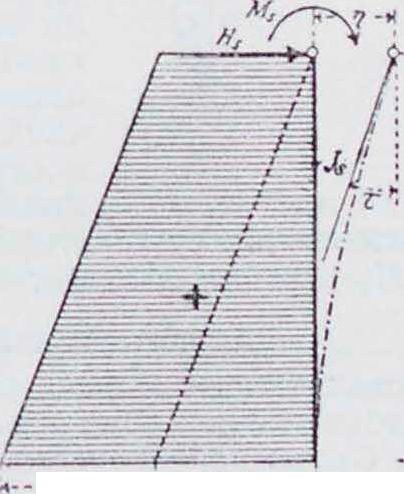
Если стойка защемлена внизу, то угол поворота упругой линии в голове стойки равен сумме элементарных поворотов относительно друг друга всех сечений стойки, то есть равен площади,

Фигура 45.

так что (по фигура 44) т=а прогиб, или мл··

смешение, η=,_FI

Из обоих уравнений следует:

ТГ ( Т.Т Λί.ΤιΛ 3, 3

ll_s=(»7EI_S--*— J _h3, r =M,s, + -

где

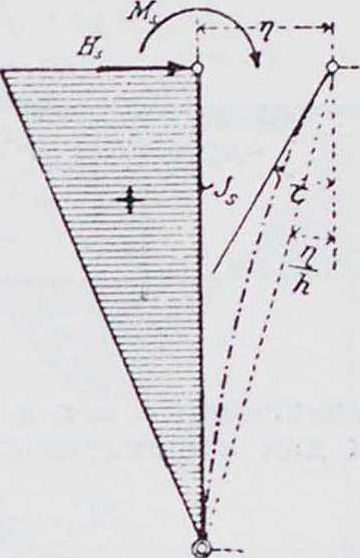
Если стойка имеет внизу шарнир, то (фигура45)

,M_S h ?h 1, V Μ_sh i Ч_ я» - j * Ml h + h“wr, + k^=M*^e*+ h

El

где

M,

h

Здесь H_s=—

Углы поворота β и а (фигура 46) находятся, как опорные реакции простых балок I и I, нагруженных фиктивной нагрузкой

,^м,. Приняв вначале, что моменты М_г и EI ^г

Mi положительны, получим:

Уравнение —β=+ а дает:

я,

U

(-!*)

Ы.)

I’

I

тренние напряжения. В расчет вводятся только те Г-ные напряжения, которые зависят от изменения длины балки. Если одна из опор неподвижна, то смещение любой стойки равноеерасстоянию от неподвижной опоры,

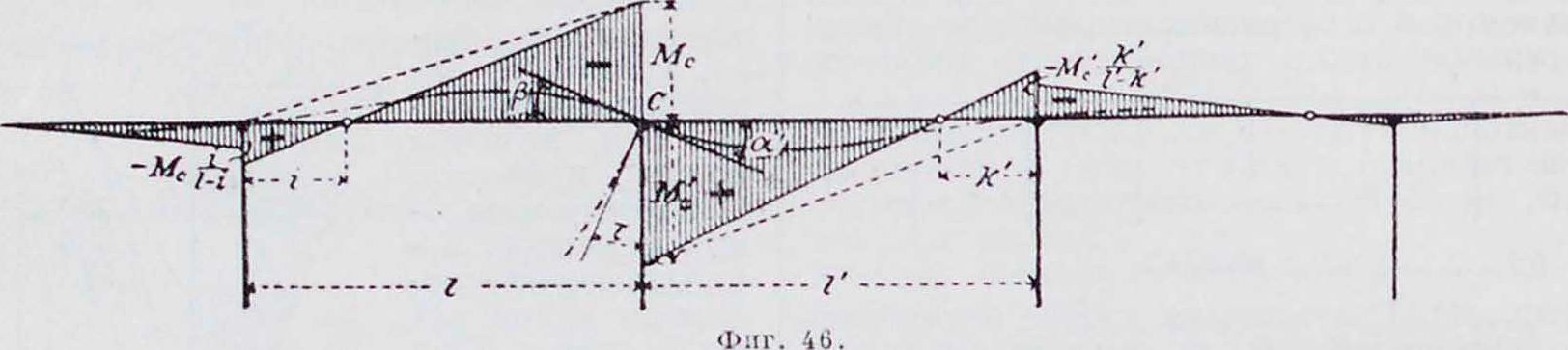
Из уравнений а — т и М_в=М_с — М_с получаем для защемленных стоек:

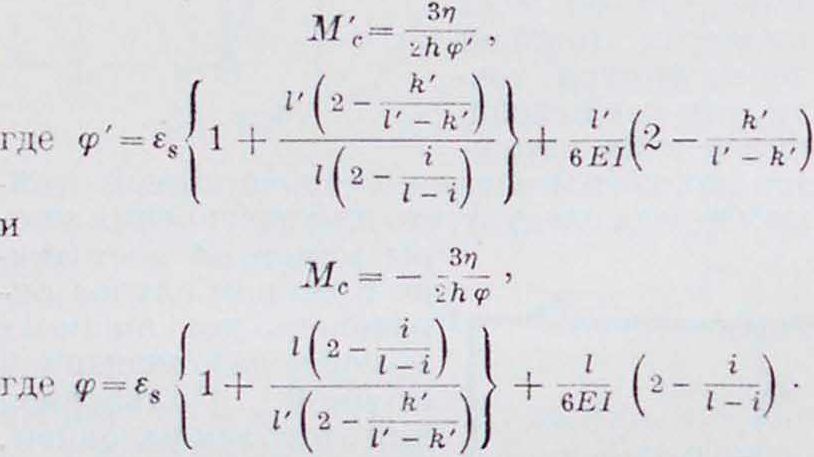
Для шарнирных стоек изменится только величина т; вместо ~, войдет, аг„ в этом умноженному на at. Для смещения каждой головы стойки, или, что равносильно, для обратного смещения нижнего конца ее, можно но вышеуказанному способу построить эшору моментов.Полученные эпюры ну-

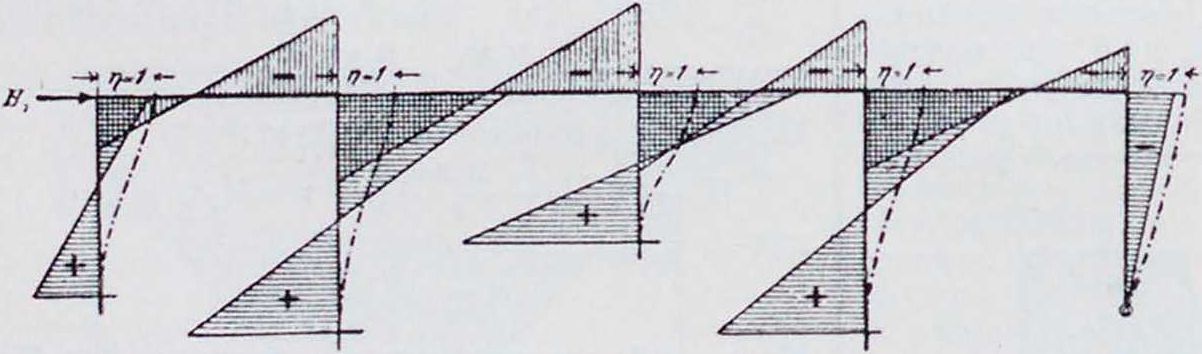
случае равно _iEj-. Выражения примут вид:

Зная переходные числа μ и вычислив по этим ф-лам опорные моменты для η=1, можно построить эпюру моментов. Когда

Фигура 4 7.

но концам балки имеются жестко соединенные с ней стойки, находят из условия и=τ тем лее путем (фигура 48):

Мα= -М» =

Ж1Ю просуммировать. В случае же симметричной системы смещение стойки пропорционально ее расстоянию от оси симметрии. Когда же нет ни симметрии ни неподвижной опоры, задаются предварительно неподвижной точкой близ середины и определяют моменты и силы II, во всех головках стоек. Если после расчета окажется, что -II,— 0, то выбранная точка действительно неподвижна и эпюры построены правильно. Если яге ϊ£Γ,=ΔΗ, то АЛ надо ввести как внешнюю силу и по ней вычислить поправки для построенных эпюр. Поправки, очевидно, пропорциональны ранее найденным моментам от Н_л при смещении у= 1.

Аналитический метод.

Аналитический метод применим лишь при постоянном по длине пролета моменте инер-

где

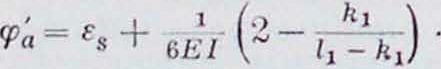
После того как из эпюр для смещений отдельных стоек (фигура 47) построена суммарная эпюра моментов, определяют Н₁^= -11,. Здесь 11, берется но суммарному моменту M_sдля смещения η=1.

Изменение температуры. При изменении 1° в Б. и., упруго связанных со стойками, возникают дополнительные вну-

ции балок неразрезных.

I. Свободно лежащая балка с постоянным моментом инерции.

Из условия, что оба угла наклона /?,. и a_r+l (фигура 49) упругой линии балки над опорой г равны мелгду собой, получается зависимость мелгду тремя последовательными опорными изгибающими моментами. Углы β и a могут быть определены как опорные давления балки на двух опорах,

нагруженной фиктивной нагрузкой ^, с пролетом I,. или 1_гИ. Опорные моменты при выводе ф-лы предположены положительными. Площадь фиктивной моментнойнагруз-ни состоит из эпюры М₀ и трапеции, определяемой опорными моментами. Обозначив через О_ги_г и P_{r +}, Ь_{г +}, моменты площадей Q_r и Ω,.₊₁ эшо]) М₀ относительно левой и правой опорных вертикалей. можно написать:

Последнее уравнение (индекс г =и— 1):

к_я_₂ 1„^ + 2М_п^ =

¹,2 Ρ·«(ί_η-ι-“)(ί«-ι + β)-^{М 1} »1-1

-г 2 Р а(1„-а)(21_п-«).

ΕΊ р_г - (2М_Г+

м,-х) +

Я а ·

ΕΙ · а, .,=> *’

5 CMi_r+

+>/,·.)+

V.l

о т. к. /?,. —а_г+1, отсюда получится так называемое «уравнение трех моментов»:

М,_, · l_r + 2M_r(l,+ lri Р-л

в

’ о

l) ~Ь ^JV,· Ι-χ · Ip ! ! —

-Q._+ib_r+1.

Р.Л. =

P « Or 11 a)

Если нагрузка в каждом пролете (фигура 49) состоит из одного только груза Р, то

^л-^вг^в> И"¹

-Р .^a6(i_r-o)(l_r + n);

^r+.iv +1 =

Mv’-H- V’)]=

=* jP e(ir + l-«)(2ir + l-«)‘

H случае нескольких грузов P в пролете величины, соответствующие каждому из них, складываются, почему уравнение трех моментов примет вид:

М_г-_Х · 1_Г + 2М_г(1_Г + l_r+l) + М_г+1 · г_г+1 =

~ I 2 Р ¹ " (Jr — ч) Дг + ") —

-Т- 2 ^р "<*·

*r + ¹

n)(2l_r+l-a).

Таких уравнений можно написать столько, сколько неизвестных опорных моментов (фигура 50). При свободно лежащих концах

Фигура 49.

Для балок с защемленными полностью концами нужно написать еще два ур-ия, предположив вместо защемления еще по одной опоре близ каждой крайней опоры, то есть прибавив по краям два бесконечно-малых пролета 7₀ и 1_п+1. Эти дополнительные уравнения следующие:

2М₀ ?,+ М, /,=- 2 ^Ра (ίι-«) (2Ιχ-α).

¹ I

M_n^ l_n+2M,_rl,r -₍ 2 P a(i„-a)(i„+a).

Для случая равномерно распределен, нагрузки р на каком-либо пролете моменты

О_га_г и Р_ГЬ_Г от площадей эпюры моментов М относительно опорных вертикалей вообще определяются величиной:

П i, (11,=-

•>-Óà г“г 3

р/2 _ р/4

8 ’ ’ :ί ~ 1:4

М, О

а потому уравнение трех моментов приводится к следующему виду:

Фигура 50.

М₀ М_п 0. Первое уравнение (индексг -1)

напишется так: Ш_г{1_г

: li) 4" М* I* ~~

- ί Σ ^р « о· - Ό Οι

«)-

M_r_₁l_r + 2M_T(l_r+

+ lr + l) + M_{r + 1} i_r-n =

i 3i

¹ r * i 4

l³.

-Pr + l

-VP.H(7₂.

п)(21₂-а).

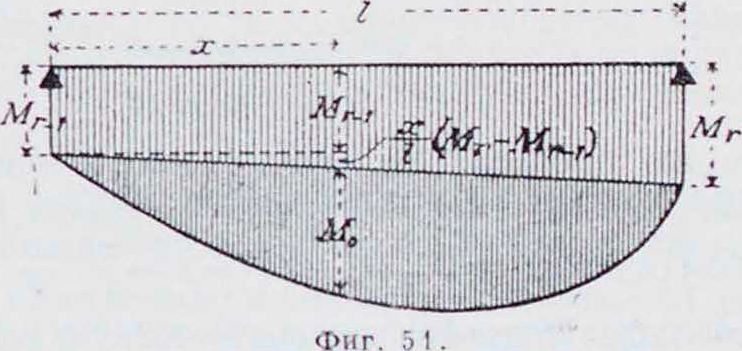
Определив опорные моменты, можно написать выражение изгибающего момента в любом сечении пролета 1_Г (а именно, согласно фигура 51), в котором опорные моменты предположены положительными:

М_т=М„ + М_г_> + * (М_г-М,._,)

Отсюда же получается выражение для поперечной силы Q_x в том же сечении:

Q,-

dM_x

dx

dU о dx

+ 1 (M_r — =

^lr

= Q₀+l_r(M_r-M_r^).

Опорные давления определяются как разность поперечных сил в сечениях, смежных с опорной точкой справа и слева от нее.

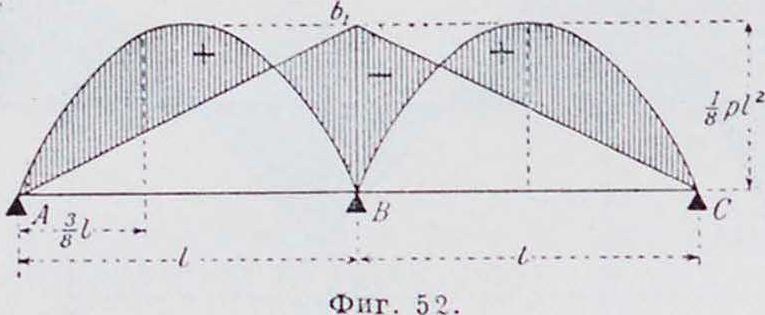
Рассмотрим два частных случая: балки 2-пролетную и 3-пролетную, с равными пролетами и нагруженные сплошной равномерно распределенной нагрузкой q.

Балка 2-пролет на я. Опорные моменты М_х=0, М₃ — 0. Из уравнения трех моментов следует, что 4M₂l=— pi³, откуда М₂ — — jPP, то есть момент на опоре

2-пролетной балки по величине равен наибольшему моменту в двухопорной балке моментов следует, что 4МЛ -)- МЛ=— J pi³, откуда М₂=М₃=— ¹ pi³, то есть меньше, чем

pi² _

₈ — момент по середине двухопорн. балки.

Па фнг.53 построена эпюра моментов этой балки. Наибольший положительный момент имеет место в крайних балках в сечении, для которого Qx=^r! — рх—¹^ =* 0,то есть при момент в этом сечении д,г V 4, 6,4 pi* _ 16 pi*

^1χ и ΙΟ ^ί 10 ¹ Ш ы “ -5 ’ 8

Опорное давление на средних опорах

В

С=2 —

Т>1²

1 υΐ

π

ίο

pi.

Если пролеты, лежащие слева от рассматриваемого, и сам он не нагружены, то правые стороны в ур-ии моментов равны нулю, и соотношения между последовательными моментами становятся постоянными, зависящими только от величины этих пролетов (фигура 54). Это позволяет определить фокусные расстояния. Из уравнения трех моментов для первых двух пролетов

2Μ₁(ί_ι + 1₂) + Μ₂ί₂=0 получим:=—2 (l + jj=— /с₂, что показы

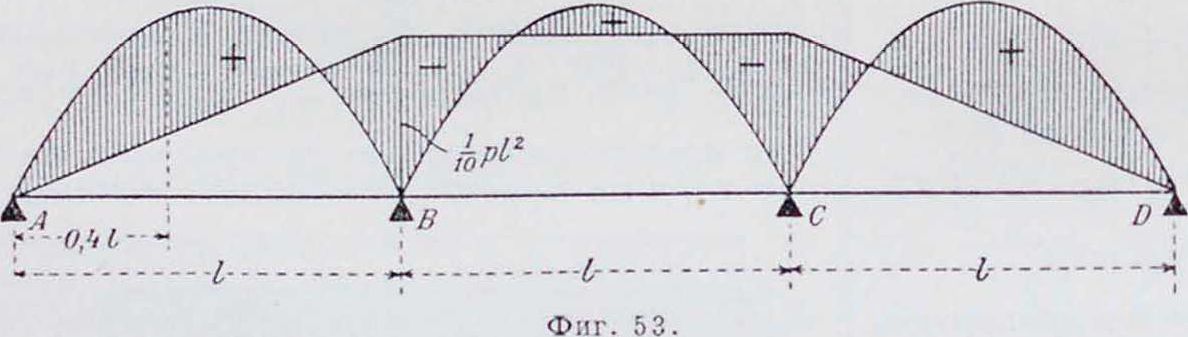
вает, что знаки опорных моментов разные и что расстояния нулевой точки или фокусной точки от опор определяются соотношением

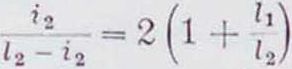
. 2 "Ь - ί 1 i

откуда г₂=-^--1₂.

того же пролета. Па фигура 52 построена эпюра моментов для этой балки. Момент в любом сечении ее M_X=^F х(1 — х) — * ^pls ;

наибольшее значение его соответствует се-_ d I „

чению, для которого Q_x= _dx= 0, а именно:

Ц--рх — -γ=0, то есть при х=³8 I, и равен

_Р 8, Λ 8, _8 I __9 pV

^Μχ~ ·Δ 8 ) 8 i 8 16 8

Из уравнения трех моментов для второго и третьего пролетов Λί,ί₂ + 2М_а(1₂ + 1₃) + + ЛГ,1₃=0; после подстановки в него отношения М₂: — к₂ получим:

и я M,

г(1

•Н») i 1| ¹

/ч /з 2h₂

— 7с₃, откуда

7с₃

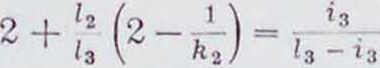
чем определяется положение фокусной точки в третьем пролете. Таким же путем определяются положения фокусных точек в ос-

	i2 ; i F	h :
А	2	~i	A
0		2	3,
i·-----1,—	—>i<-----i2 —	- - ·*Κ;------*

?k-I	FK	P К	С
A	A	A	A
i<-2	к-ι	к	к“
Г-----*·κ-ΐ	— ·*·.	ί/c-----*7*" *

54.

Фиг.

Опорное давление па среднюю опору

В

pi. pl». р!. pi* 2 + 81 ^ 2 ^ 8i

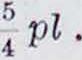
В балке 3-пролетной опорные моменты М_г и А/₄ равны нулю, опорный момент М₂—М₃, а потому из уравнения трех тальных пролетах. Вообще для фокусных точек всех пролетов

^ь.-² + ег5(²-*Т

Если в том же порядке пойти с правого конца балки, то легко можно вывести соотношения для определения положе-

ния правых фокусов, а именно: к_п — 2 + + (2 — jp—у Зная положение фокус ных точек, легко построить эпюру моментов для всей балки, если будут известны опорные моменты загруженного пролета. При загружении одного /с-го пролета уравнения трех моментов для него и смежных с ним напишутся так:

ί*_,+ 2Μ*_, (i*_, + 1_к) +М_к · г“= -6^?g-⁴, М_к-г h + 2М_к(1_к + 1*4.,) -1- М_{к н}, · 1*4-,= — ·

Их можно представить в таком виде:

-Π*ί* + м“_,г“	[2 + V (2 +	мк «	1 е°*ь‘
		Мк-,1.	J 0 ‘к
мк~1 h + м“г“	[2+т(2+	мк., мк !.	]—6аг

M*-,

но так как * М_к-2

1

^ 1

и

М к +J

Λί*

*А+ i

то эти уравнения приводятся к виду:

Решая их относительно M*_, и М“, получим:

6«*(b*fe; - а“) 60*(а“ь*-ь*)

^ь~¹“ Ц( -Щ) · ’

если воспользоваться готовыми таблицами Laederer, Griot, A. Cart et L. Portes идр., в ко орых даются непосредственно ординаты линий влияния при нек-рых соотношениях между пролетами. Таблицы Мерша (M6rsch, Eisenbetonb iu) дают значения М_ж и Q_x в случае, когда нагрузка передается через узлы.

В л и я н и е ос а д к и оно р. От не-р гвномерной осадки опор у_г искажается oci» балки и появляются дополнительные изгибающие моменты. При отсутствии нагрузки осадка вызывает эпюру моментов, состоящую из трапеций в каждом пролете. Углы поворота от осадки (по фигура 55), умноженные на жесткость,

ΕΙβ,.=¹~{2М_Г + М_г_,) и Ь7«_г+1=¹ (2М_Г + M_rri).

Как видно из фигура 55,

Р_г + ^аг+1=9» + <5 + ψ-δ ;

Рг + ^ar i

Ur - Ur -

^λ +

Ur — Ur +

W *Г+1

Из написанных равенств выводится уравнение трех моментов

М_г_х 1_Г + 2M_r (l_r -f l_r+ i) + М_г4-χ · l_r.f i =

GEl

l/r - Ur-1, Иг^; ir ^ Ir

Λ

+ 1

Это уравнение с разными индексами г можно написать столько раз, сколько неизвестных опорных моментов.

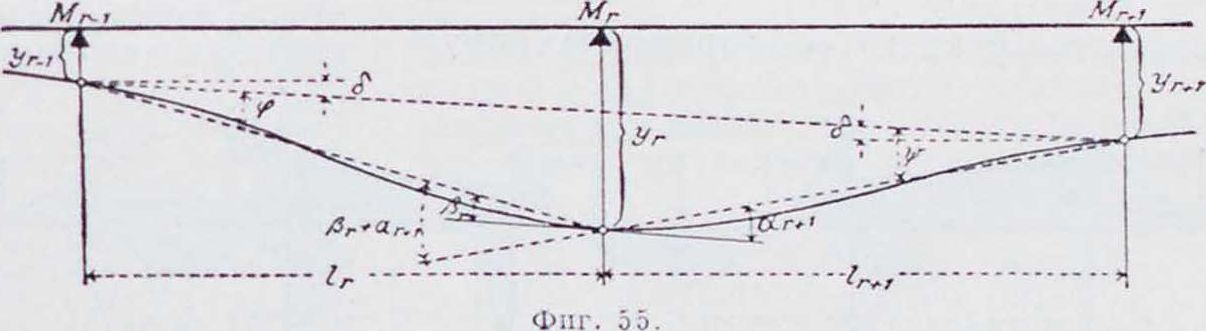
которыми определяются опорные моменты в любом загруженном пролете. Так. обр. расчет моментов Б. н. при загружении одного пролета сводится к определению фокусных точек. Следует отметить быстрое убывание опорных моментов, идущих от загруженного пролета. Наир, при всех равных пролетах отношения фокуси. расстояний будут к._г=4, /с₃=3,75, А-₄=3,73 и т. д. Если предположить, что загружен четвертый пролет и по его загружению известна величина А/₃, то

“ + Γ7ϋ ^³’ ^{а М1=—} 4 3/75 ^{= —} ,5 ^Мз‘

II. Свободно лежащая балка с меняющимся от пролета к пролету моментом инерции.

Если момент инерции балки меняется при переходе от одного пролета к другому, оставаясь постоянным внутри каждого пролета (фигура 49), то уравнение трех моментов приводится к виду:

Такое быстрое убывание моментов дает возможность при расчете многонролетных балок не принимать во внимание удаленных балок. Пользуясь выведенными формулами, можно вычислить опорные моменты в каждом загруженном пролете, построить по ним отдельные эшоры, затем геометрически просуммировать их и таким образом получить эпюру от полной нагрузки. Пользуясь уравнениями, определяющими влияние одного загруженного пролета, можно построить линии влияния, для чего потребуется последовательно загружать грузом Р= 1, располагая его в разных пунктах отдельных пролетов. Определив опорные моменты н опорные давления, можно при помощи выражений для М_х и Q_x составить ур-ия линий влияния для каждого сечения. Построение линии влияния облегчается,

^мг-г У;+°~Мг +м_г+1 ^ =

—P-a(l_r-a)(i_r + a)-

Λ, Σ^ρ·°(ν+ι~α)(2l_r+x-a).

При равномерно распределенной нагрузке вместо каждой суммы войдет.

4

III. Б. н., упруго защемленная в стойках, с постоянным моментом инерции.

Формулы для вычисления фокусных расстояний выводятся из условия равенства углов поворота упругой линии. В балке (фигура 5G) рассматриваем два ненагруженных пролета; нагрузка находится справа от них; углы — т=/?_г_, и также т=а_г; кроме того,

T — M_se_s. Это приводит к двум уравнениям:

-ил - -&{*»+*.>-<*:

+ ма-«М--7}

r-t

Фигура 56.

Вставив в первое уравнение выражение М_$ив второго и решив относительно г_г, получим

/,·

з +

¹1 Ur-1 ~>г-0 i__Iг

W-i (2 ~ 3V-i) 6EJ · вг-i

Аналогично определяется правое фокусное расстояние (смотрите фигура 57). При свободно

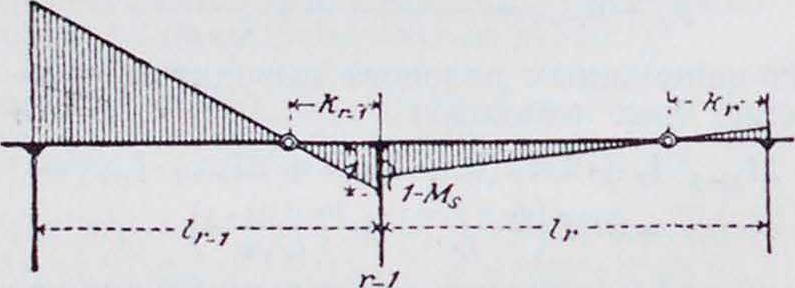
Фигура 57

опертых концах балки первое левое фокусное .расстояние г_х=0; при защемленных полностью концах г_х=; при концах упруго опор. Обозначив через [М] и [М"] статические моменты площадей М₀ относительно правой и левой опор, а остальные обозначения взяв по фигура 58 и считая все моменты положительными, получим следующую систему уравнений:

1. а„ т„, что дает —J (ΙΜά + ЛОЛ мas

(,и_я- М

4КО,

2» fif,=- «ft, что дает

3. - /ii, — Tj, что дает

“βίί ^{(2Mft+ м)еь} (ί/,-ΛίΟ J*·*

4. β₀ — — а_с, что дает

.к, -ь4^(2М+л/)·

5. а_с - т_с, что дает

6Е ^{+ Ыл)=(Мс} - ^Μί) ’< ^(Mr ~ ~ 4К1_Г

6. /i, — а,/, что дает

^.₇(2лон-.vow_b;.V^2m;

7. —fid ^{= T}(h ^что дает

М_с) -

|ЛГ|

4 /·;

-А-<ш_й+м;,

ЛГ,/).

ы<1

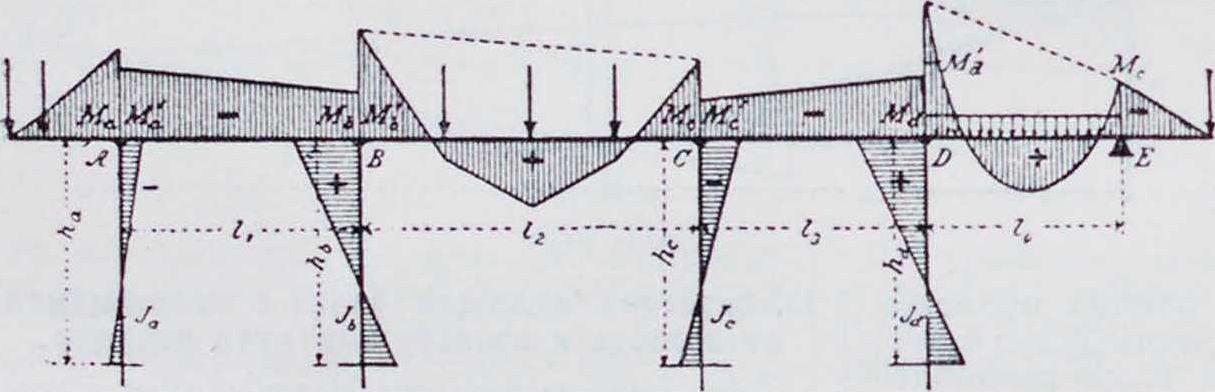
Таким путем можно написать столько ур-ий, сколько имеется неизвестных. Для стоек с шарниром внизу надо положить f_s =. Загружая только крайний правый пролет, можно определит!, все левые фокусные расстояния г и переходные числа μ и аналогично при загрузке крайнего левого пролета—все фокусные расстояния к. Опорные моменты от нек-рого малого смещения η можно найти, решив столько же уравнений, выражающих зависимость между вызванными смещением углами поворота упругой линии в узлах. Угол поворота в голове стойки, смещенной на величину μ при з а щ е-м л е н и и ее внизу.

τ=М.

где

Фигура 58.

защемленных (жестко связанных с крайни-

з -

ми’стойками) г₁

6E1sq

h

IΗ

Последние выражения, дающие тот же результат, что отношения e: е на фигуре 36, получатся из общих формул, если представить за крайними стойками еще бесконечно-большие пролеты 1₀ и („х, которые вследствие бесконечной длины настолько гибки, что не препятствуют деформации системы. Статически неопределимые опорные моменты балки при любой одновременной нагрузке всех пролетов м. б. найдены решением системы ур-ий, выражающих равенство углов поворота β, а и т упругой линии балки и

^: Mg +

⁸ 4Б-/,

а при устройстве шарнир а:

h

^{где 8}» ‘ШГ„

Взяв обозначения по фигура 53. получим систему уравнений:

1. п_а=Тд, что дает

^h (iM„ + м_ь)=м_пяс„ +

ΒΕΙ 2- fib

2h_lt

м ah π, 3»? Ы η 2/ь,

(ib, что дает

„£,(2Мь+Μί) (2mUm_c).

Фигура 50.

) Mft_s^£b + что дает (2M_C + Ml)

3η

2h/,

J»

~ HEI

(M/,-Mi) h/, 4 Ei_b

(2 M + Μ_Λ).

3. n/, tj>, что дает

Ш^(2М* ^{+ М}

4. «з — a_c

Ш

5. a_c **» т_с, что дает

β1·/^{(2 M} + *<*> - + Z ⁽ - ^M£,4E/_c

e. fi, - - α,ι, что дает

l.

вШ&М_а + M_r) - J;_f (2Mrf + -v/_f) · 7. ал τ,ι, что дает

6Εί ^{<2 h,;}

8. -/S_f- г_е, что дает

Зч

2h/,

3η

2hr

3η

М_е)

1.

HEI

(2M_e+ M _d)

Μ

h_r 3η ^e Mile 2/1,.

Эти ур-ия применимы и в случае разных моментов инерции в отдельных пролетах. Такая же система ур-ий дает возможность определить моменты от изменения f, если только вставить в уравнения соответствующие каждому узлу значения перемещений г - ±alL, где L—расстояние узла от неподвижной точки.

Лит.: Т и м о ш е н к о С. II., Курс сопротивления материалов, 5 изд., Μ. II. 1923: II росит-

II м п о и Л., Строительная механика, ч. 1. М. 1925; М ю л л e р-В р е с л а у Г. Графическая статика со-оруж., пер. с нем. СПБ, 1908—13; Ч> и л о н с и к о-Бородич Μ. М., Основы теории работы упругих енл в плоских системах, М. 1925; Г а б и н о в и ч

11. м., Применение теории конечных разностей к иееледов. неразр. балок, М. 1921; II о д о л к с и и ii И. С., Строительна!! механика, ч. 1. М., 1924; Т и м 0-

III е и к о С. 11. Курс статики сооружений, ч. 1. Л., 1 20; А к п м о в - II e р е т ц Д. И. Статика сооружений. Неразревные балки на жестких опорах, Л. 1 927; справочные таблицы: inkier К., Vertrage и her Briiekenbau. Theorie d. BrOcken, II. 1. Wieu, 1875; Carl A. et Portes L., Calcul des pont.s im talliques par la mithode des Iignes d’influence, I·. 1895: Lederer A. AnalytUche Ermittelung ii. Anweiidung v. EinflusellniCH, H. 1908: 9 r i n l G., Kontinuierliche Balken init konst. Tragheitsmoment. liiterpolierbare Tabellen. Zurich, 1916; Kapferer V. Tabellen der Maximalquerkrafte u. Maximalmo-Hiente durehlaul. Trager. Berlin, 1920; M firsch E., Der Eisenbetonbau. 5 Auflage, Stuttgart, 1022—26; Ritter V. Anwendungen d. graph. Statik, T. 3, Zurich. 1900; I a n e I 1 о 1. Der durchgehcnde Tra-ger au Г elastlscll senkbaren Stfltrcn, «Ztscur. d. VDI», H., 1904, B. 48, p. 128 u. 161; L (: v у M., La s t a tillin’ graphique, Paris, 1886 (теорема о двух моментах): Μ II 1 1 e г - В г e s 1 я u H. Die graphische stalik d. Baukonstruktionen. H. 2. T. 2. Lpz. 1896; It I I 1 e I’ M. Iler kontinuierliche Balken auf elastisch drehbaren Stiitzcn, Zurich. 1918. см. также «Schwei-

ягг Bauzuttung», Zurich. 1911. В. 57; Snter E., iirrechnung d. kontlnuierl. Balkens. I!. 1916; S uter Г. Die Methode d. Festpunkte. Zur Berechnung d. statisch unbestiih. Konstruktioiien, li. 1923;S t r a s s-ιΐ·ι· A. Berechnung statisch unbestimmter Systemc, Г. 1, 1!. 1921; M 6 r s c Ii E., Berechnung d. durchlauf. iialkens. 1926; Г 0 p p I A. Vorlesurigeii iiher tcchni-s · 11» Mechanik. H. 2- liraphische St Hik, Lpz., 1922.