> Техника, страница 18 > Балки простые

Балки простые

Балки простые, ix Б. п. принято относить балки, которые перекрывают один пролет, независимо от их статической определенности (балка, свободно лежащая на двух опорах, с заделанными концами ндр.), или большее число пролетов, но при условии их внешней и внутренней определенности (балки с консолями Гербера). Важнейшие формулы для расчета В. п. для часто встречающихся случаев сведены в таблицу (смотрите ниже). При помощи последней путем сложения или вычитания табличных результатов м. б. получены расчетные данные и для более сложной нагрузки, не указанной непосредственно в таблице. Так, например,

£7

Шшпптт^©

: А

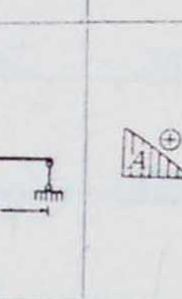
расчетные данные для случая, изображенного на фигуре 1А, можно получить как разность данных для случаев по фигура 113 и 1В, давая значение:

0=(Р-<7). р;;

Закрепление на опорах предпо- ^с лягается в ненапряженном состоянии, и достаточная подвижность в горизонтальном направлении одной из опор имеет место во всех балках.

I. Обыкновенная балка. Рассмотрим подробно свободно лежащую на двух опорах балку, находящуюся иод действием постоянной сосредоточенной и сплошной нагрузок, указанных на фигуре 2. Значение опорной реакции А определяется из условия равновесия между активными и реактивными силами, по моменту относительно точки b, равному 0:

Фигура 1.

А=r ped + P_t (l - «j

Р-г d - ⁽h)

= vc<l + )^]P(l-a),

1

H

в соответственно 71 — ! pc (i — d) +, У Pa.

1

Величина поперечной, или срезывающей, силы Q (равнодействующая касательных напряжений) η каком-либо сечении балки определяется из условия равновесия между

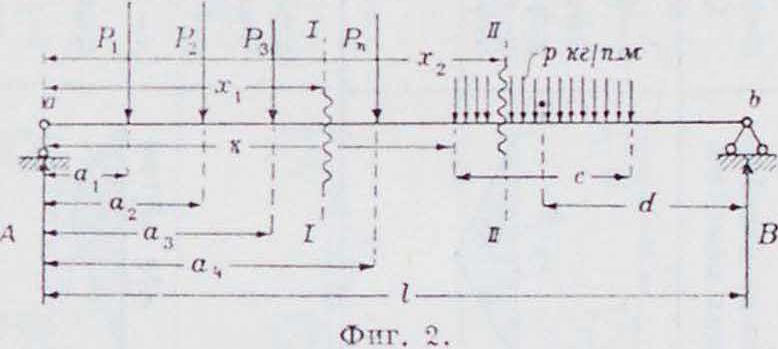
внешней и внутрен. силами левой или правой половины как проекция сил на вертик. ось. причем при рассмотрении равновесия правой половины знак берется обратный. Для сечения 1—I

i -

В — pc — Vji

I

и для сечения II—II п

Qn-A-JlP−pto-k)-

О

= -[В-р(с-х._г + 7е)].

Величина изгибающего момента в сечении (момент внутренних сил в сечении) определяется как момент левых или правых сил относительно сечения: в последнем случае он берется с обратным знаком.

У tdo) Q,=А — У Р =

/л ¹ I JmU

Г. Э. 7П. II

О

№	Балка с расположением нагрузки	Эпюра поперечных сил	Эпюра изгибающих моментов	Место и величина Qmax “ Qmin	Место и величина Мmax “ Mmin
1	m hi -*t>L	j tEjSZSl		зс=0 Qmax^* 71=в~¥	х — а м - 1‘аЬ м max — J-
2	—лг.-ι /V и/Λ.Γ is тл i-°, !: —x» —		ςΑα (Ββ-α-ψ	х=0 Qmax~ ^ = τ(^-ί) х=1 (*+ 0	с ( с При д:=α+— 11 - а- - •Vmax— Jf(l “ а ~ 2 )·τ " Р*’
2а	y?			х=°. X=J Qmax™ А “К 2
	fTliimili			*-«. "	Л =. ΛΙ *»«*” 8
3	V JlTnTgrrr^ £ J i	Θ (ЯШттп^. _ ^ЩЩВ| Θ	1	* “ о Qinax=A~?l х=* 1 Qwin^B=^	1 Х==2 Мтах=γ2
4	(Ж^ pl	Χ4πΐί!0Ρ771		*1=0 О, =В-Н* vmin — u — g j	При ж,=2d± ϊ£ 3d=, p/ca.c (*-d) β Vi с
	i i i1 a "c u-i-x,— 2

!£L

Θ

Qmax^ — ^·

x-= l

Q min ⁼

pi

V 3

M max=0,064 pH

Ht>Mi

(?

Af,

ITu3

~7У;

x=0

_Qmax„A-’^M,j^

x—l

Mi- M,

X=i

А 111 fIX— Ai 2

Qmin=^D=-

l

ΓΗ	lP i
L„L

ЯШ

к

шло

x=*0

A=Q„,ax=^a

-*(·«)

x=l

B—Qtnin**

-(•S-S)

£06 a² Mvmx- _t

X=0

Mmin— —a— j Pa²b

- V„ =

Pab²

- M_b —

l

-Щ1Щ]

.v=0

i

ЛГ. M,

ίί<π—Д

^Ч1Ш1Ш13Р^Р^

Qmax - ¹"^:

x—l

Qmin—ll— ^

i=

M " -EL^a

mux — „4 x=0 M min

___M _pL*

- ^Λί«-ΐ2

θ

ВШШьь.

X,

Γ>ί) <

-V»

ж=0

Qmax—A -x=l

pi

i

p!

pH

x=0

32

Mmin--M “⁼<jg P‘²

ir

Ci

____*

P

5ЬтЧ

nem

У.

Θ ^Мь ^XJI111У дД1 ©

.т=0

Q in αχ— А — с с з с⁴

•Кг

*-1. “,

4И ⁺ 10Н

У^1

Ас

Μ ηιαχ - M _а -f Ах - Ц-^1

Qmin⁼B —~Г~ А

м-0; М min--М _а-

⁼ё5J, ⁽¹⁰¹*^с* - 1°г^зс+зс«:

и.- ^р (^,сЯ ®*

^Ь 4И 3~ δ]

Балка с располо- Эпюра поперечных Эпюг а изгибаю-‘ ^? жением нагрузки сил щих моментов

9а

©

М„

IK©

£-*n_ J

I

ки.

Ik©

Шппь.

^цщ]

Место и величина Место и величина

Qmax 11 Qmin	М max 11 М min
х=0 Qmax~ ^ ~*>о Х=1 Qmfti-B=|dpi	*=<(l -]/" 10 )· мта. п/2 Μηιίί W а — , pi2 - ,ft= 80
т=0 Qmax™ А Р ~~ В х“*1 Qmin™ В~ Р(1-а)Ца+21) 213	Λ„ α (1 — Ь)·(21 + 6)6 “me 2ί« χ=0 V ν ρ,^/; «•тол ш a 2/2

JC-0	x—0; Mmtv -- - .Vf Λ
Qmax— Д - g Pi	*-?ί
Qmin™ В ™ g Pi	wax =y§8 Pi2
д:-0	X=0
Λ, 111 1 Qmax“Д — Pi	Mm/»- - M« Pi*
x=i	A HI
	f 384
	15. Ill „
	•“»вх” “ -.mpl2+mxJ
Q“®» Λ“(ΙΊ) Ma l x-l	x=Q; M mj n— — M aV /2 t. d/«, /М3
	2c/2 15 4 6
	2.4c *—F c p“
pc* Λία<?тш=й=—	M max™ Ma + Д·^- ^1

х=0 Qmax х=1 Q1ПI н

о	р/2 .τ^ 0; Mmin™ ~ Ма=~ §
д -; р о	,/, /" 7
	6
β=Ιρ,	, р(* 2, P-V* М„,„х---Γ6 + 7ΡΧ~Ύ(

Μ

ΐ>

Qmax

Α— ^ ^ Μ _mi_n=* - Μ_α=

2 I

-щцщ^

15

Ы

i_

-d —

x=0 до с

Qmax⁼

x=l

М„_|Лг=М

х—с

М min — ~ Μ η— Pc

piaiQ^ng IflilMiw

x=l

Qmax — A — Pl

β

Qmax’ ·^:

pc

x=i

Р

Q max—Д^— Ϊ

win — “ Λί (j —

pi*

M min— ~ -W«—

pc*

*=

*mV ^; ~ M a—

p/²

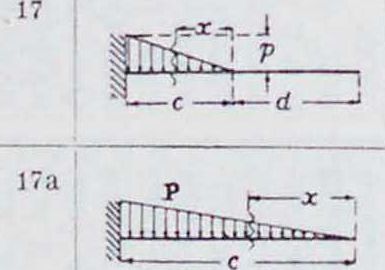
18

д:₂=0

Q — A __ ^ Ч11ЮХ— ¹

.X— с до

Qm«x=A^

x.»=0

J)/²

x—l

M tit in — - M a —^ ^

i-

20

-НЧ)

Q=0

x=0 до 1

At max— A!

Для сечения I—I

I

31 j=Ахj — ^ Р (ар — а)=— [li (i — ар) — о

1

— рс(1 — ар — d) — У! Р (a — Xi)].

Для сечения 11—II

II

I

31 _и=Ах₂ — 2 Р (^J,2 — и) — р

(ас,-Ь)¹ 2

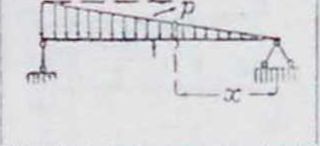
А.Равномерио распределенная временная нагрузка.Пусть она действует на участке произвольной длины с. it равняется р на единицу длины (фигура 3). Наибольший изгибающий момент надлежит отыскивать в пределах длины с:

м_х=Ах — р - « -1] х - р &Ψ-

Для заданного х (определенное сечение) )жение нагрузки определяется ^*=0, отсюда z=x (l—[) · Наи-

опасное положение нагрузки определяется d м_х

из условия.

~ αζ

больший момент в сечении имеет значение:

м_я

- ₂^С,) t¹ - Т) -

Для определения абсолютно наибольшего момента выбирают сечение на расстоянии

d VT

х, удовлетворяющее условию _dx^x=0, к-рое определяет что а;=“; для этого сечения

( с

^{: х} t^{1 —} i)

Т. е. абсолютно наибольший момент имеет место, когда равнодействующая сплошной временной нагрузки совпа-

р кг/TLM

дает с серединой балки, и равен

U ~^pc(l- ^с *“«в» 4 V 2 Г

Для случая с=I (когда временная нагрузка покрывает весь

Фигура з.

pi*

. Наибольшее значение ле-

пролет) М_тах - ₈

вой реакции, равное наибольшей поперечной силе, соответствует случаю, когда г — 0. В этом случае

Наименьшее значение той же реакции соответствует случаю, когда нагрузка сдвинута к противоположному концу пролета, —

A_min=^. При полном загружении пролета,

при с= I, опорная реакция Α·=^ρ.,¹. В более сложных случаях нагрузок определение наибольших значений реакций, поперечных сил и моментов лучше всего производить при помощи линий влияния.

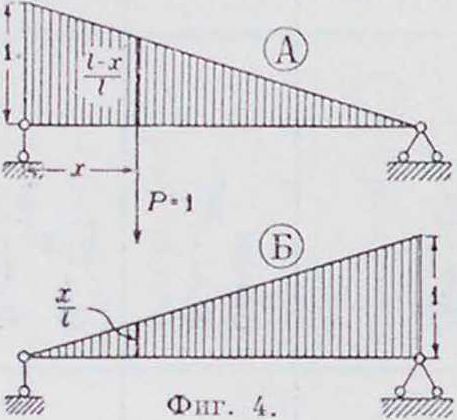
Б. Линии в л и я н и я графически изображают изменение момента поперечной силы, опорной реакции и др. в определенном месте сооружения при действии на него подвижного груза, равного 1. Каждая ордината линии влияния, которая измерена иод местом положения груза, определяет величину указанного усилия или момента при положении груза над ординатой (смотрите Линии влияния). 1) Ли н и я влияния опорного давления. Полагая, что на балку действует только один груз Р=1. имеем: А=¹ _;^л и В=“; оба эти уравнения представляют собою прямые линии, легко строящиеся из их анализа: при ж=0 А=1 и В=0; при х=1 /1=0 и В= 1;

на фигура 4, А и Б построены эти обе линии влияния. 2) Л и н и я в л и я и и я м о-м е н т о в Выражение моментов изменяется в зависимости от того, расположен ли груз справа или слева от сечения. В первом случае М_а—Аа. Это—л и -ния опорной реакции А, измененная в масштабе 1 а. Применимость ее ограничивается только правой частью, то есть длиною b. Во втором случае из равновесия правой части следует, что 31_а—Вb. Это—линия опорной реакции В, измененная в масштабе 1 b. Применимость ее ограничивается только левой частью, то есть

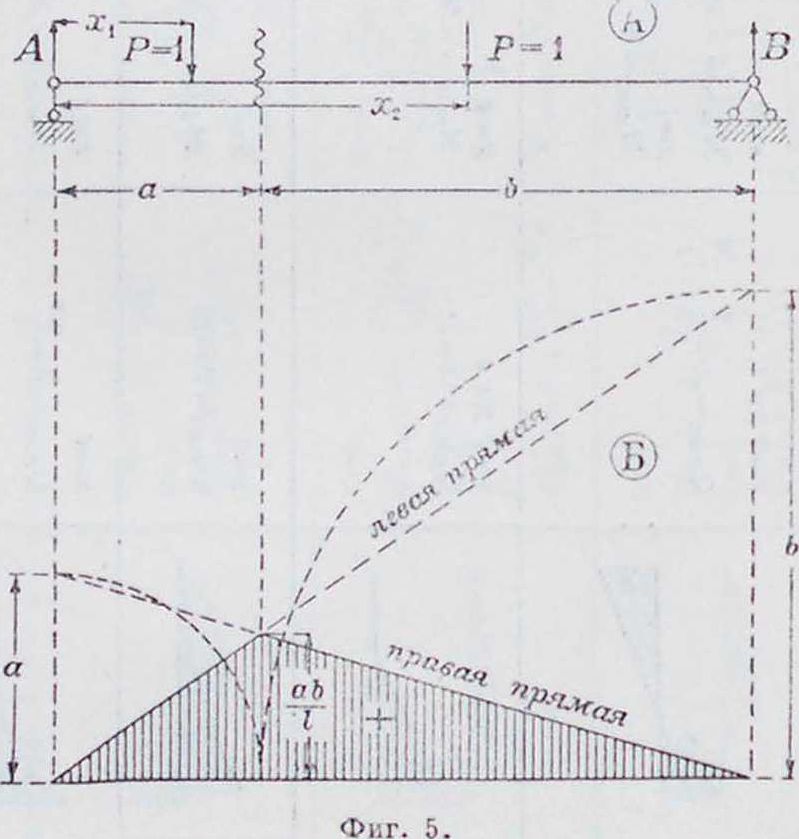
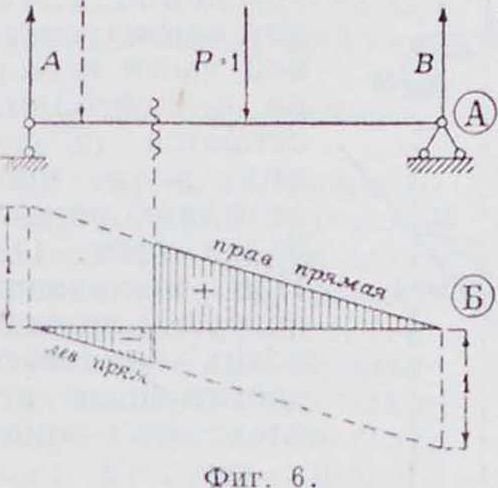
длиною а. Окончительи. вид линии влияния указан на фигуре δ, Б. Следует заметить, что независимо от конструктивных особенностей систем левая с правой прямой всегда пересекаются на вертикали под точкой моментов. Это свойство дает возможность по одной прямой (хотя бы правой) построить левую, так как каждая из прямых имеет нуль на своей опоре и общую ординату под сечением. 3) Л и и и я в л и я и и я поперечи ы х сил. Величина и знак поперечной силы в сечениях двухопорной простой балки также изменяются в зависимости от положения груза относительно сечения. При положении груза справа от сечения Q=A, при положении слева от сечения Q=—B=A—1. Обе эти прямые приведены на фигуре G, Б, на которой показана окончательная форма линии влияния Q. 4) Л и и и и

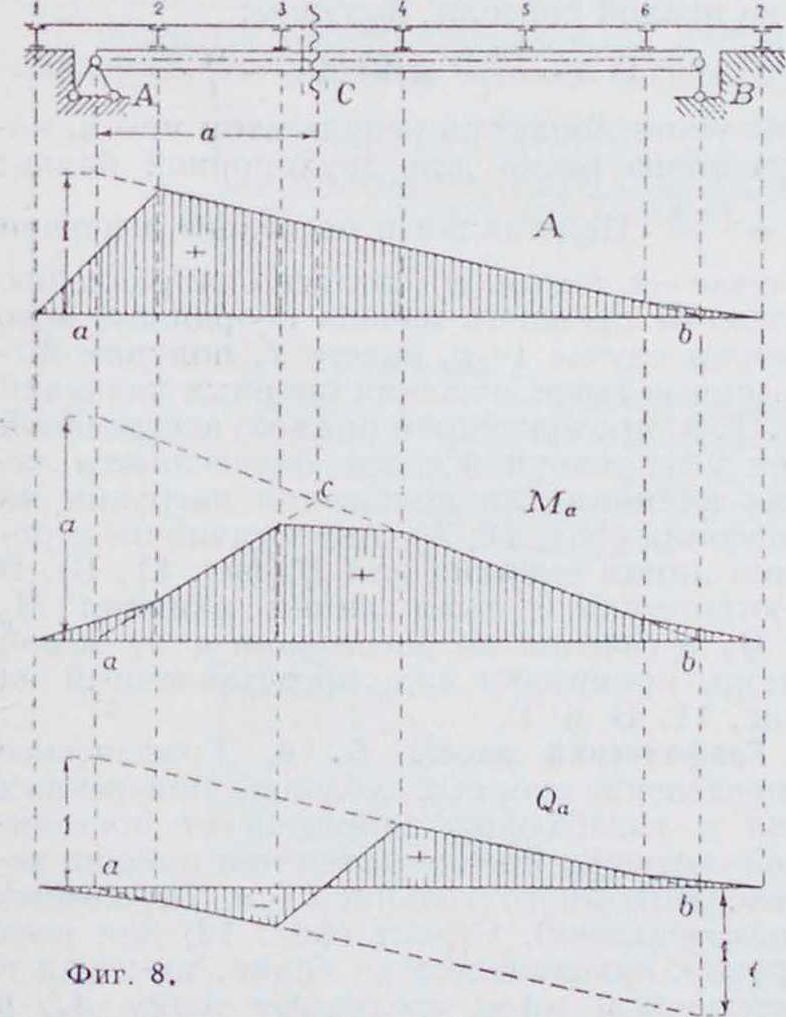
η л и я н и я и б а л к о, у а д е л а иной о д н и м к о и ц о м. По предыдущему, при грузе слова М„ —1-х, Q_rt=—1; при грузе •справа (из равенства левой части) М_а—·О, (J_a О. По этим выражениям построены лилии влияния М_а и Q_a (на фигура 7).

При наличии в сооружении узлов или передаточной нагрузки линии влияния изменяются между узлами но прямой (фигура 8) и являются многоугольником, вписанным в линиювлияния при непосредственном действии нагрузки, с вершинами под узлами. Указанное является следствием того, что передаточные балки2—

2, 2—3 и т. д. передают нагрузку на узлы 2, 2, 3 и т. д. но закону рычага.

Пользуясь линиями влияния, можно определить самое невыгодное положение времен, нагрузки и вычислить наибольшую величину момента Ми попер, силы <3 в сечении балки (смотрите Линии влияния).

В. А б с о л ю т и о и а и б о л ь ш и и .момент. Отыскание абсолютно наиболь-

I В !

9-

г гг прав прочая

Ш	1 1	тграк. прям
I 1. -	1	Фигура 7.
Пси прям.

м„

шего момента связано с определением опасного сечения и того «критического“ груза, который в этом сечении делает абсолютно наибольший момент. Если бы критический груз был известен, то для определения положения опасного сечения необходимо было бы нагрузку на балке расположить т. о., чтобы середина расстояния между критическим грузом и общей равнодействующей совпадала с серединой балки (фигура 9), то есть чтобы иыло удовлетворено условие: х — (теорема Винклера). Но так как и критический груз вообще неизвестен, то задача сводится к его отысканию, что делается путем ряда проб; следует иметь в виду, что за редки-

2 I

λ С О О О #_ ¹Q Q. Q.Q-H

1

I___ j__♦ i_

2 2

Фигура 9.

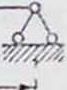
ми исключениями критическим грузом для абсолютно наибольшего момента является тот, который для середины балки делает относительный максимум, то есть удовлетво-

m j, i jg

ряет условию: j · · Найдя по о этому условию критический груз Р_т, определяют опасное сечение из условия х=и уже затем проверяют, удовлетворяет ли оно помимо требования опасного сечения требованию критического груза для I I 1 J^H.

него, то есть _}{ ^ -Р < < j_{ 2 ^{Если ыа}"

о о грузка передается на балки через передаточные поперечные балки, то сечение с абсолютным максимумом совпадает с положением одной из поперечных балок, ближайших к середине пролета.

II. Двухопорные нонсольные балки свободно лежат на двух опорах и имеют концы, продолжающиеся за опоры (фигура 10, А). Нагрузка междуопорной части изгибает только ее. При загружении консолей происходит изгиб и консоли и междуопорной части. Условия работы консолей аналогичны

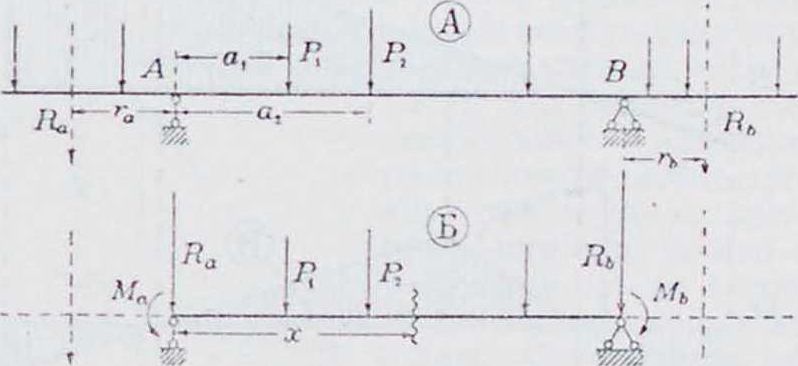
Фигура ю. бруску с защемленным концом. Влияние же консолей на междуопорную часть аналогично действию моментов на опорах М_а и M_h. величина которых равна произведению равнодействующей нагрузки консоли на расстояние ее до опоры: M=Rr (фигура 10, Б). Зная величину опорных моментов, вызываемых загружением консолей, можно .междуопорную часть балки рассматривать как балку, свободно лежащую на двух опорах и находящуюся под действием между-опорыого загружения и опорных моментов.

Величина левого опорного давления такой балки А=R_a + А₀ + j (М_а — М_ь), где 1!_а —

равнодействующая нагрузки на примыкающую к ней левую консоль,

Л о — опорное давление двухопорной балки от загруже-ния междуопорной части,

(М₀ — М_ь) — опорное давле ние от загружения опорными моментами. Аналогично величина правого опорного давления определится следующим выражением :

В=Н_ь + В₀ +

1

Ь--

D

+ (М_Ь-М_а).

Величина поперечной силы в сечении междуопорной части определяется из выражения:

<?*= Л - νρ=ρ„ +

О

+ (М_а-М_ь),

где <Эо—поперечная сила, как к простой двухопорной балке. Изгибающий момент в рассмотренном сечении определяется из следующего выражения:

стон оалки, лежащей па двух опорах, от загружения междуопорной части.

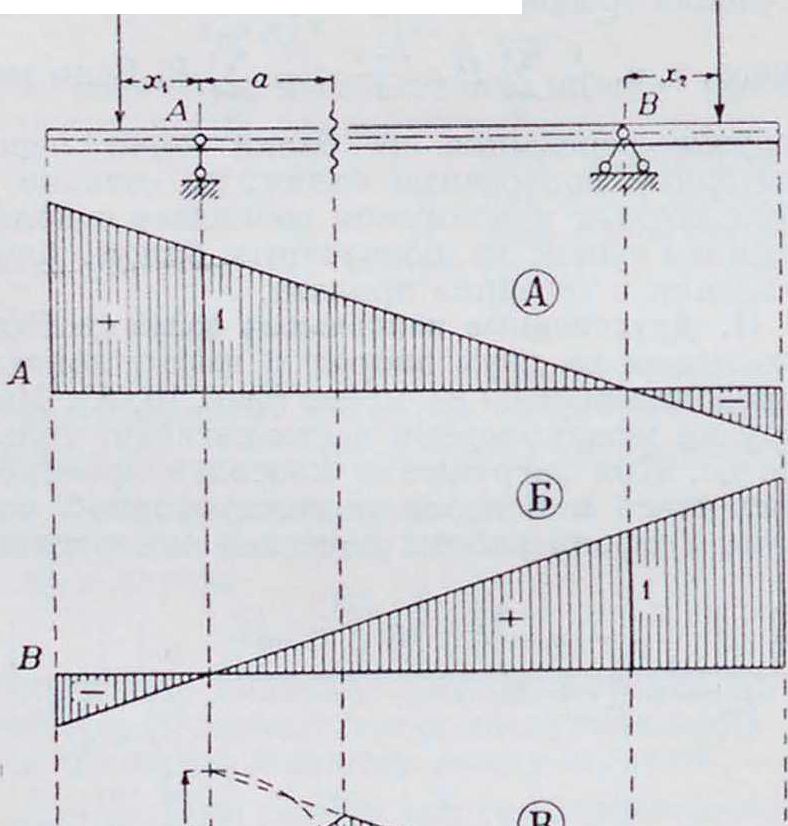
Л И Н И И В Л И Я II И Я. Т. К. КОНСОЛИ При нагрузке междуопорной части не оказывают на последнюю никакого влияния, то линии влияния в междуопорной части в балке с консолями остаются те же, что и в простой двухопорной балке (фигура 11). При положении нагрузки на консолях является достаточным исследовать закон

1 1 М„ 1	а чТТг· 1 * vfffr * fi ! 1 Util!.|: ,:i.	гтг^ ^ 1 тТТТгтт^ i 1 111тТггт>^ i 1
ί	W i	1 1
1 1 q„ ί	ISfliJ.: III	© ______ ;
		i 1
	Фигура 11.	""•--4.1

М _х - Ах - У] Р (« - а)=М₀ ~ М_а ‘, — - М„ “, о где М₀—момент в том же сечении, как иро-

Фигура 12.

изменения опорного давления, все же последующие линии влияния (М и Q), как зависящие только от опорных давлений А и В, построятся без особого на то анализа. Полагая последовательно груз - 1 на левой и на правой консоли, получим:

1=и 2) А=— ^л’ ·

Эти ур-пя являются результатом ур-ия, полученного ранее для двухопорной балки:

I — х

А= -η— Подставляя в последнее в первом случае—а;, вместо х (согласно направлению влево от прежнего начала координат) и во втором случае 1+х_г вместо х, получим выведенные выше значения опорных давлений А. Т. о. продолжением прямой, построенной для междуопорной части, определяется линия влияния для положения нагрузки на консолях (фигура 11, А). Аналогично же строится линия влияния для В (фигура 11, Б). 1! соответствии с этим линии влияния М„ и Q_a в сечении иа расстоянии а от левой опоры принимают вид, представленный на фигуре 11, В и Г.

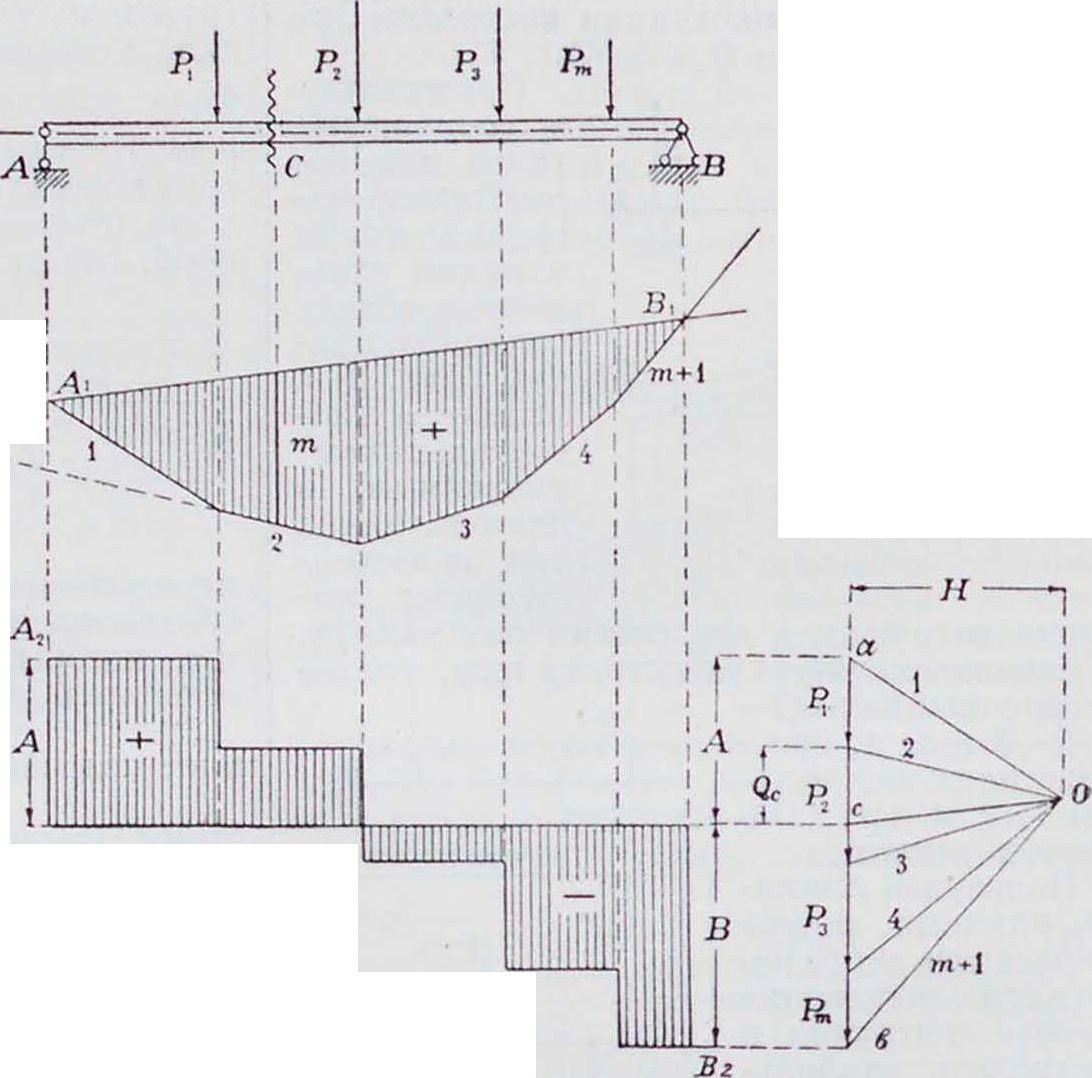
Графический расчет Б. п. Графическое определение опорных давлений, поперечных сил и изгибающих моментов от постоянной нагрузки производится при помощи веревочного многоугольника (смотрите Веревочный многоугольник). Строят (фигура 12) для всех грузов, находящихся на балке, мн-к сил и веревочный мн-к; соединяют точку А_г, в которой первая сторона веревочного мн-ка пересекается направлением реакции А. с точкой В_г, в которой последняя сторона пересекается с направлением реакции В.

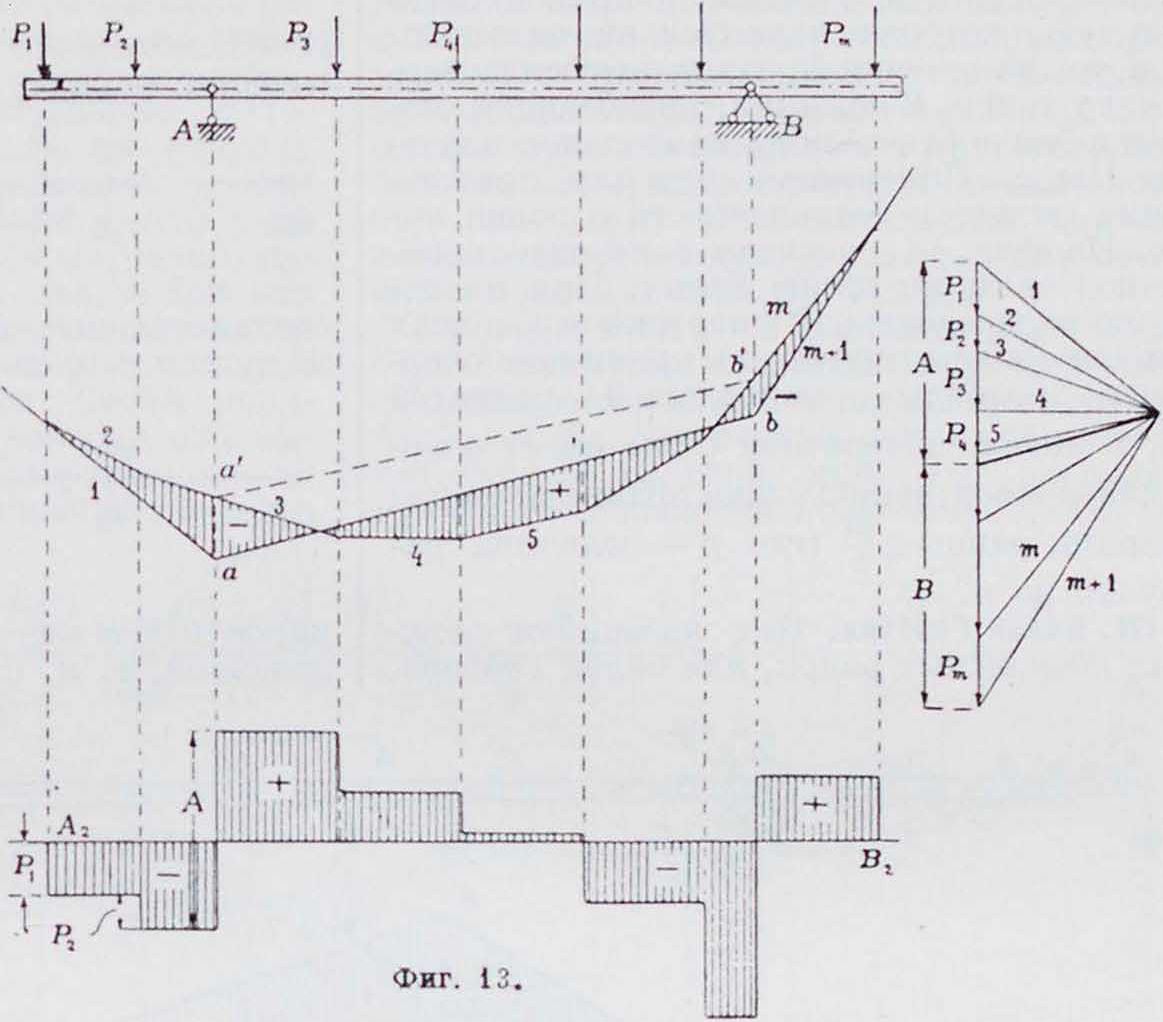
моментов применяется также для двухопорной балки с консолями (фигура 13). По-прежнему положение замыкающей стороны а—Ь эпюры моментов определяется пе ресечением крайних сторон 1 и и + 1 с вертикалями опорных точек. Части эпюры, лежащие ниже замыкающей, положительны, лежащие выше нее—отрицательны. Из выведенного выше выражения момента для такой балки и из фигура 13 видно, что эпюра моментов междуопорной части слагается из двух эпюр: эпюры моментов тп_д простой двухопорнои балки, очерченной веревочным мн-ком 3—4.т с замыкающей стороной а—Ь, и эпюры, очерченной трапецией ааЬb, от действия отрицательных опорных моментов М_а и М_ь, определяемых отрезками аа и b bЭти последние определяют собою положение за-в мыкающей ab в консольной балке. 15 отличие от двухопорных простых балок эпюра моментов консольной балки при загружении консолей всегда имеет отрицательную часть эпюры, поэтому наибольшее значение расчетного момента проверяется в двух сечениях: положительное— в средней части балки и отрицательное — на опорах.Ступенчатая линия А_гВ₂ представляет эшору поперечных сил.

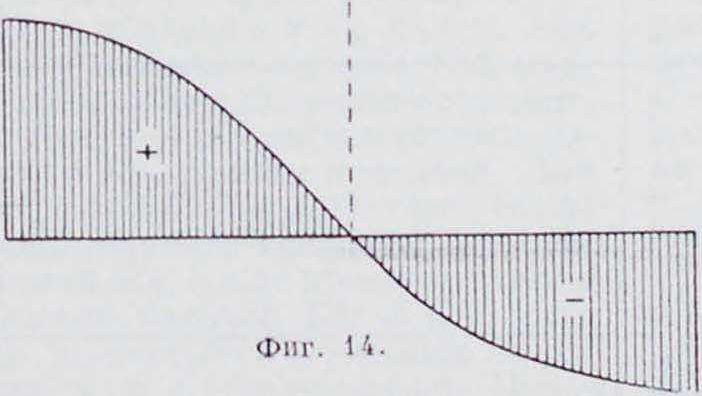
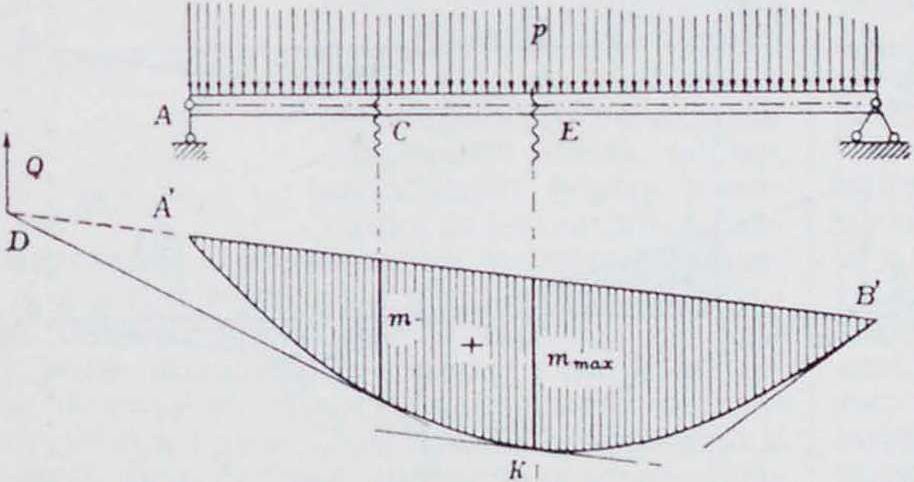
Если на балке находится сплошная нагрузка, то веревочный мн-к переходит в веревочную кривую (смотрите Веревочная кривая и фигура 14). При таком загружении для нахождения положен и я и величины поперечной силы для какого-либо сечения балки проводят касательную к веревочной кривой в точке, лежащей на вертикали сечения С. Точка пересечения

Подучают прямую h, В, называемую з я-м ы к а ю щей. Если провести затем через полюс О мн-ка сил луч О—с, параллельный замыкающей стороне Л₁В₁, то отрезки с—а и с—Ь определят величины опорных давлений Л и В. Поперечная сила Q,. для сечения балки С равна равнодействующей из А

С

и 2 1‘- Она проходит,

о по теории веревочного мн-ка, через точку пересечения сторон веревочного мн-ка, охватывающих эти силы, т.е. через точку D. Величину и направление находят из многоугольника сил. Ее статич. момент относительно сечения С — «изгибающий момент», действующий на балку в этом сечении,— но теории параллельных сил равен полюсному расстоянию Н, умноженному на ординату ж. Если сечение С передвигать по пролету от А к В, то поперечная сила изменяется скачками и ее изменение на эшоре представится ступенчатой линией Л_гВ_г. В то же время ордината ж. определяющая моменты в сечении балки, описывает всю площадь между веревочным мн-ком и замыкающей стороной (площадь эпюры моментов).

Описанный способ определения опорных давлений, поперечных сил и изгибающих этой касательной с замыкающей стороной определяет положение поперечной силы, а луч, параллельный касательной, вместе с лучом, параллельным замыкающей,— ее величину и направление. Изгибающий .момент для сечения С опять равен М — тН. Если провести к веревочной кривой касательную, которая параллельна замыкающей, то для сечения Е, находящегося на вертикали точки К касания, изгибающий момент п балке будет иметь наибольшее значение Нт_тах. Поперечная сила для этого сечения лежит в бесконечности и равна нулю. На фигуре 14 показано изменение поперечной силы по длине балки. При равномерно распределенной нагрузке веревочная кривая (эпюра моментов) принимает очертание параболы с наибольшей ординатой ре „

.и эпюра поперечной силы имеет очертание кривой; наибольшие ординаты ее над опорами равны ± ^ (где р — величина нагрузки на п. м).

ill. Балки Гербера. Под названием сложных консольных балок, или балок Гербера,

между собой и с береговыми опорами при помощи промежуточных балочек CD,CJJ.

А	В Х п А	B	D
	X С дД Фигура 15.	с	ШИ.
В общем виде они представляют собою мн>-топорную балку, в которую при помощи
л	В J J л	и	If
ёг		Й. C	А

Фигура 1G.

соединительных шарниров включены про-

межуточные	балочки.	Наличие	этих шар·
А В		11! к	D
Р ^>-с	С В Ϊ W//.	т	* к
	Фиг.	17.

ниров делает конструкцию статически опре-деленной, т. к. е введением каждой новой

Фигура 18.

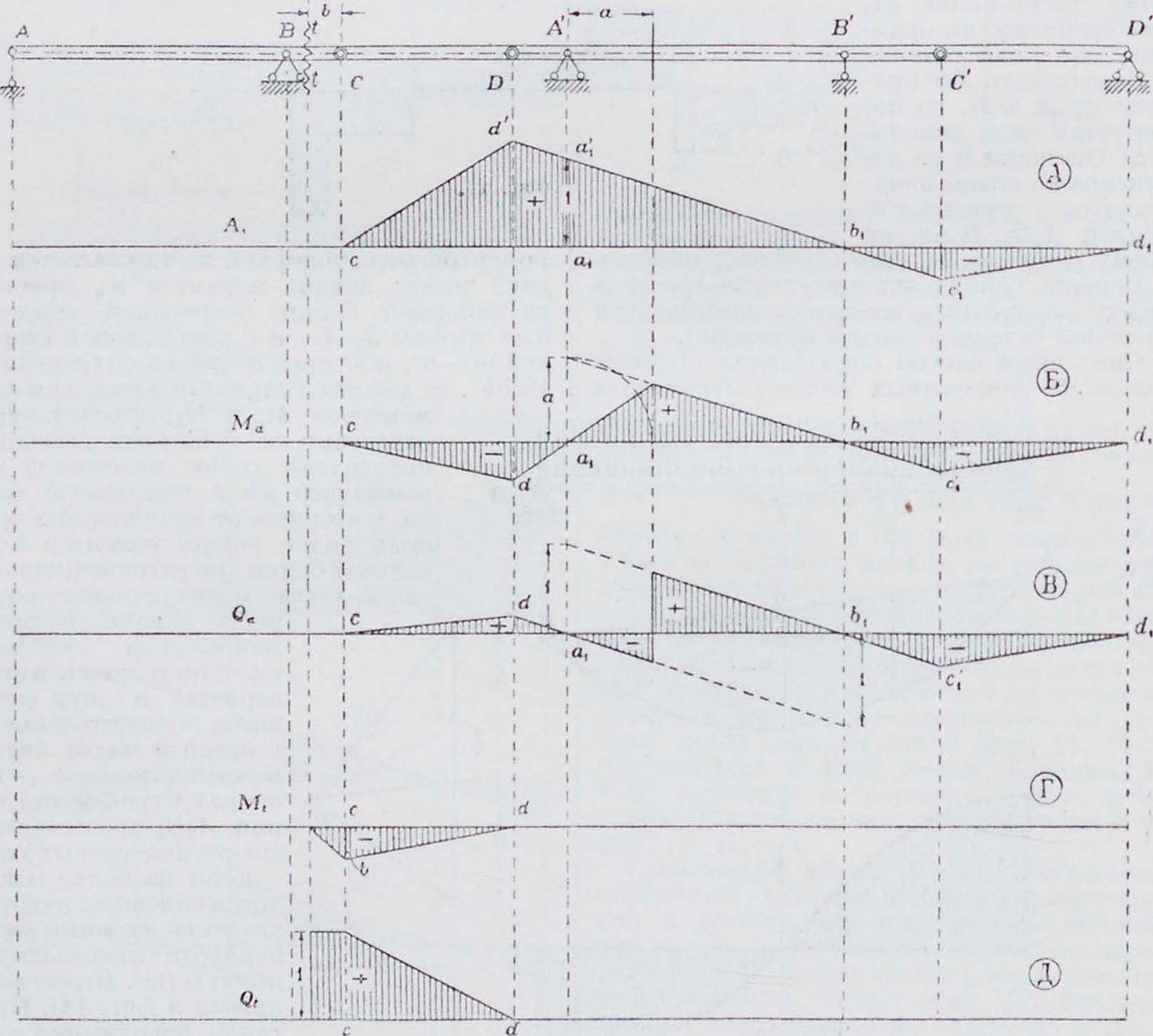
подразумевается система (фигура 15), состоящая из простых консольных балок ЛИ. ЛВ’, концы консолей которых соединены опоры или пары опор добавляется один или пара шарниров. Общее количество шарниров «так. обр. равно излишнему количеству опор п без 2, т. e. s — n—2. Расположение шарниров должен быть сделано так, чтобы удовлетворялись условия геометрическ. неизменяемости, которые при достаточном числе шарниров влекут за собой статическую определенность конструкций (смотрите Неизменяемость геометрическая). Междуконсольные балочки CD, CD, шарнирные но концам, по существу являются баночками, свободно лежащими на двух опорах, независимо от того, будут ли они опираться на консоли (балка CD) или будут подвешены к ним {CD). Эти балочки работают и деформируются только под действием нагрузки, лежащей непосредственно на них, и так как они представляют собою балочки, лежащие на двух опорах, то расчет их производится так нее, как этих последних. Своим опорным давлением на концы консоли они вызывают деформацию прилегающей консоли и в соответствии с этим ближайших между остальном протяжении системы имеет ординаты, равные нулю. Аналогично линии влияния моментов и поперечных сил (фигура 1В, Ii и В) в любых сечениях консольной балки сохраняют свою форму и метод построения, как в простых консольных балках; на протяжении нее междуконсольных балочек CD и CD линии влияния дополняются прямыми cd п c[d_x, проходящими через вершину ординат линий влияния на концах консолей и нуль под шарниром у другого конца балочки. Это распространение линий влияния на длину дополнительных балочек имеет место и в линиях влияния для сечений в консолях (фигура 18, Г и Д).

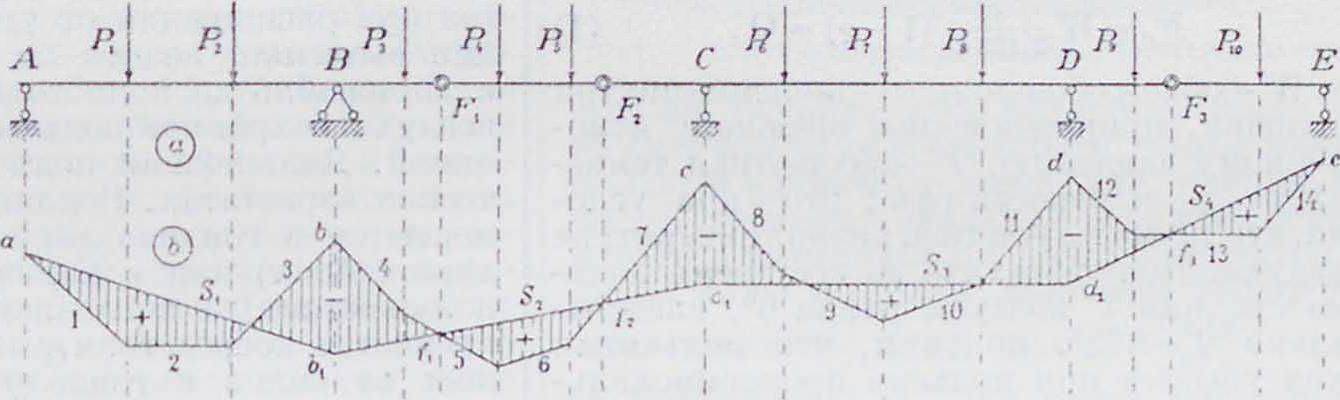
Г р а ф ический расчет балок Гербера. Рассмотрим сложную балку (фигура 19). находящуюся под действием системы грузов Р₂,., Р₁₀. Для построения эпюры моментов строим силовой мн-к для нагрузки 1 —Р₁₀ и, задавшись полюсами О, 0₂, 0₃

А л,

р

в.

1

•

; А !

; г. ч^я ·

vl:

^;6

п

©

I

Фиг. опорных частей (фигура 1G). При загружении только основных консольных балок междуконсольные балочки хотя и получают смещение своих концов (фигура 17), но вследствие шарннрнос.ти на концах сохраняют свою первоначальную форму и никаких деформаций, а следовательно и напряжений не испытывают.

Л и н и и в л и я н и я сложных консольных балок отличаются от таковых же для простых консольных балок учетом влияния междуконсольных балочек при движении по ним груза. Так как по отношению к консольным балкам междуконсольные балочки носят характер передаточных, то линии влияния в пределах этих балок, как между узлами, должны очерчиваться прямыми, проходящими через вершины ординат, соответствующих концам передаточных балок·. или, что то же, концам консолей. Для простой консольной балки АВ (фигура 18, А) линия влияния опорного давления А определилась прямой da b,с[; с присоединением междуконсольных балочек CD и CD линия влияния дополняется прямыми cd и c[d_x (шарниры С и С подвижные). Передвижение груза в пределах остальных балок системы никакого влияния на консольную балку АВ оказывать не будет, а потому линия влияния опорного давления А на

19.

и 0₄ с одним и тем же полюсным расстоянием 11, строим для каждого пролета многоопорной балки веревочные мн-ки, придерживаясь в построении последовательного порядка. Снося затем на стороны этих многоугольников шарнирыF,F₂ ii F₃, определяем положение нулевых точек эпюры, через которые должны проходить стороны замыкающей. Так. обр. в пролете ВС замыкающая займет положение b_x c_lt проходящее через нулевые точки /, и /₂, и отсечет над опорами В и С отрезки bb_x и сс_х, определяющие собою опорные моменты М_ь и М_с. Величины опорных давлений определятся, если в каждом силовом мн-ке провести соответствующую ему замыкающую; отрезки на силовом многоугольнике, отсекаемые этими замыкающими, определят величины опорных давлений, причем сопротивления промежуточных опор будут слагаться из двух опорных сопротивлений смежных пролетов: В=h, + /А. C^C₁ + C₁, и т. д. Поперечные силы определяются из условий равновесия левых сил на вертикальную ось.

. Ium.: Велихов II. А., Теория инжен. сооружении, выл. 1. М., 192»; К и р η и ч ев В. Л., Основания графической статики. 5 изд., Л., 1924; Под о л ь-с к и и II. С., Строительная механика, ч. 1, М., 1924; II р о с к у р я к о в Л. Д., Строит, механика, ч. 1. 6 изд., М.—Л., 1925: II р о к о ф ь е η И. И., Теория сооружений, ч. 1, М., 1926; С и м и н с к и и Р. К., Строит, механика, Киев, 1919; Т и м <> ш с и к о С. И., Курс сопротивления материалов. 5 изд., М.—И., 1923; его же. Курс статики сооружений, ч. 1, 2 изд., Л., 1926; М юллер-Брсслау Г., Графическая статика сооружений, т. 1, перевод с немецкого, 2 ИЗД., 1908. Н. Безухов.

С,Р

]р Д

Р.

г

-Р

1б

->0*

/14