> Техника, страница 25 > Броуновсное движение

Броуновсное движение

Бр0ун0всн0е движение, хаотическое никогда не прекращающееся движение мелких частиц, взвешенных внутри жидкости или газа, поддерживаемое тепловым движением молекул; впервые наблюдалось англ, ботаником Броуном в 1827 году с помощью микроскопа. Исследование этого явления показало, что движение частичек тем интенсивнее, чем мельче самые частицы, чем меньше вязкость жидкости и чем выше ее температура. Оно не имеет ничего общего с движением частичек, захваченных потоком жидкости, так как можно установить, что направление и скорость движения одной частички совсем не связаны с движением соседней, даже очень к ней близкой частицы. Так же точно Б. д. не зависит от электризации, от освещения, от сотрясения или от какой-либо другой внешней причины. Оно целиком определяется причинами внутренними, никогда не прекращающимися, и таким образом служит убедительнейшим доказательством существования непрерывного хаотического движения молекул в неподвижных на вид жидкостях или газах. Винер в 1863 году и затем, с гораздо большей ясностью, Гун в 1888 году высказали такое толкование Б. д., но только в 1905 году Эйн

штейн дал количественную его теорию, которая была затем проверена и подтверждена Перроном. Мы представляем себе, что в состоянии теплового равновесия каждая молекула жидкости или газа находится в непрерывном движении, причем скорость достигает нескольких сот м в ск. В газах, где расстояние между молекулами сравнительно велико, молекула движется прямолинейно до первого столкновения сдругои молекулой. Здесь она быстро меняет как направление своего движения, так и скорость его. Б воздухе, при нормальном давлении, число таких столкновений отдельных молекул достигает нескольких миллиардов в ск., и каждый раз меняется характер движения. В жидкостях, где молекулы настолько близки, что все время влияют друг па друга, их движение еще более сложно и запутано. Если в эту кишащую массу молекул поместить большую твердую частицу, то молекулы в своем движении будут на нее наталкиваться с разных сторон и с разной силой. Если частица велика, то число испытываемых ей отдельных толчков громадно, и действие их, в среднем, уравновешивается; за данное, даже очень короткое время она успеет испытать столько же толчков справа, сколько и слева, столько же сверху, сколько и снизу, и в результате мы ничего, кроме равномерного, всестороннего, сжимающего ее давления (гидростатическое давление), не заметим. По чем мельче эта частица, тем меньше число испытываемых ей за данное время толчков, и здесь может оказаться, что в один момент толчки справа перевешивают толчки слева, в другой момент перевешивают толчки снизу, в третий—спереди, потом, быть может, сверху и т. д. Каждый такой перевес толчков с определенной стороны двигает частицу и перемещает ее. Если мы и не видим непосредственно отдельного молекулярного толчка, то мы замечаем, как они все кидают частицу то в одну, то в другую сторону. Ясно,что чем меньше частица и чем сильнее испытываемые ей толчки, тем резче будет размах ее движения, которое и наблюдается как Б. д. Действительно, опыт показывает, что чем мельче частица и чем выше температура жидкости, тем сильнее броуновское движение.

Перейдем к количественному описанию Б. д. Движение частички в жидкости так сложно и столкновения, испытываемые ей с окружающими молекулами, так часты и случайны, что проследить и вычислить точно закон движения было бы невозможно. Но зато эта же частица и случайность столкновений позволяют определить нек-рые средние значения. Говорить об определенной скорости Б. д. не приходится, потому что не только величина, но и направление скорости изменяется самым хаотич. образом. Эйнштейн предложил измерять среднее удаление частички от данного ее положения через определенный промежуток времени. Простое, сравнительно, рассуждение показывает, что за двойной промежуток времени частичка удаляется, в среднем, не на двойное расстояние, а гораздо меньше. Действительно, движение частицы за первую половину этого времени совсем не связано с движением ее за вторую половину; она может с такой же вероятностью уйти еще дальше вперед, как и вернуться назад или пойти в сторону. Соединяя прямой линией начальное положение частицы с ее конечным положением, мы увидим, что эта линия будет замыкающей стороной тр-ка, составленного перемещением частицы за первую и вторую половину. Т. о., эта линия может оказаться вдвое длиннее, чем удаление за первую половину наблюдаемого промежутка времени; но может случиться, что частица вернется назад, так что длина этой линии будет равна нулю; возможно, конечно, и всякое промежуточное значение. Если среднее перемещение за единицу времени мы

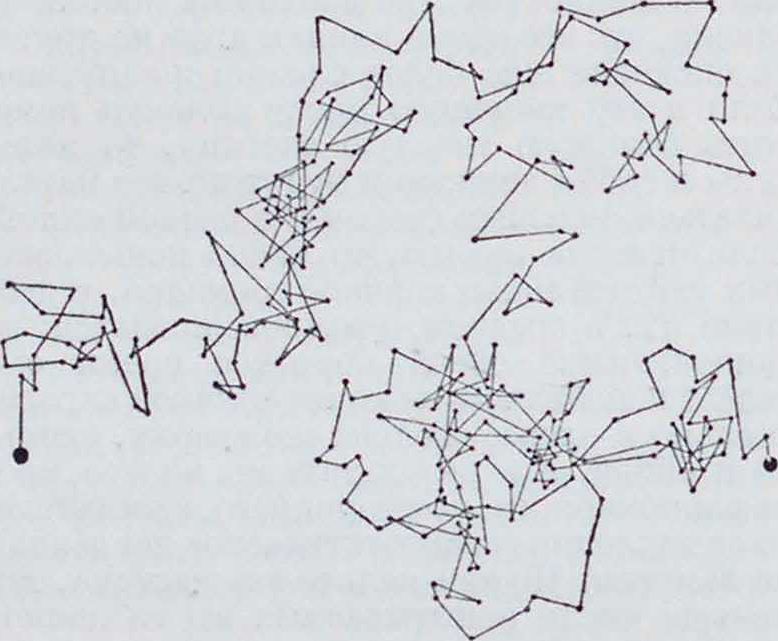
Броуновское движение частички гуммигута в воде. Мелкими точками отмечены положении частички через каждые 30 ск. (Но Перрону.)

обозначим через х, то такое же среднее перемещение за следующую единицу времени может быть направлено под каким угодно углом к предыдущему, от 0 до ±180", причем каждый из этих углов встречается одинаково часто. Вычисление показывает, что среднее перемещение за двойной промежуток времени мы получим, если представим себе, что направление перемещения за вторую единицу времени было перпендикулярно перемещению за первую единицу времени. Величина этого перемещения но гипотенузе, как легко видеть, будет равна х V2. Если мы прибавим третью единицу времени, то те же соображения покажут, что перемещение за три единицы времени равно хУз, а за п единиц времени xVn. Таким образом перемещение частички, участвующей в Б. д., пропорционально корню квадратному из промежутка времени, или, что то же, средний квадрат перемещения пропорционален промежутку времени.

Теория Эйнштейна приводит к следующей формуле для перемещения х шаровой частицы и за промежуток времени t: ^х*= £ Т Здесь R выражает газов, достоян., равную 8,313 10⁷ Tpa-lyg ; N—число молекул в грам-молекуле, равное 6,062-Ю²³, следовательно _v=1,37· 10^-1β; Т—абсолютная темп-pa; η— коэффициент внутреннего трения жидкости и и—радиус шаровидной частички. Рисунок,

сделанный Перроном но наблюдению под микроскопом одной частички гуммигута в воде и отмечающий положение частички через каждые 30 ск., показывает характер В. д. Неррену удалось установить аналогичный закон Б. д. и для вращательного движения частички в жидкости. Указанная ψ-ла позволяет вычислить число Ν, пользуясь наблюдениями над В. д. Измерения Перрена дали величину несколько ббльшую истинной вследствие того, что движение частичек вблизи стенки испытывает большее трение, чем внутри жидкости. Как показал ученик Перрена, Константен, если перечислить наблюдения Перрена, учтя это обстоятельство, то мы получим правильное, приведенное выше, значение Ν.

Законы В. д., справедливые для любых частичек в любой жидкости, могут быть перенесены и на движение молекул. Как оказалось, они весьма удовлетворительно выясняют явления диффузии и позволяют судить о размерах молекул. Б. д. послужило основанием для широкого развития стати-стич. физики и в частности метода флуктуаций, весьма плодотворного не только в области молекулярной физики, но и для теории лучистой энергии и электронных явлений.

Лит.: II « р р о к Ж., Атомы, иереи, с французского. Москва, 1925; Einstein A. Untersuehung и her (I. Theorie (1. Brownschen Bewenunycn (Λ» 199 серин «Ostwaid’s Klassiker der exakten VVissenscloirt· », I.eipzis. 1922). А. Иоффе.