> Техника, страница 95 > Бьефов сопряжение

Бьефов сопряжение

Бьефов сопряжение, соединение потоков, находящихся на разных уровнях при различных условиях сопряжения каналов. Изучение вопроса о Б. с. преследует цель найти такую форму Б. с., которая обеспечивала бы наименьший размыв русла и позволял# бы обойтись без особых дорого стоящих мер или приспособлений по предохранению русла от размыва.

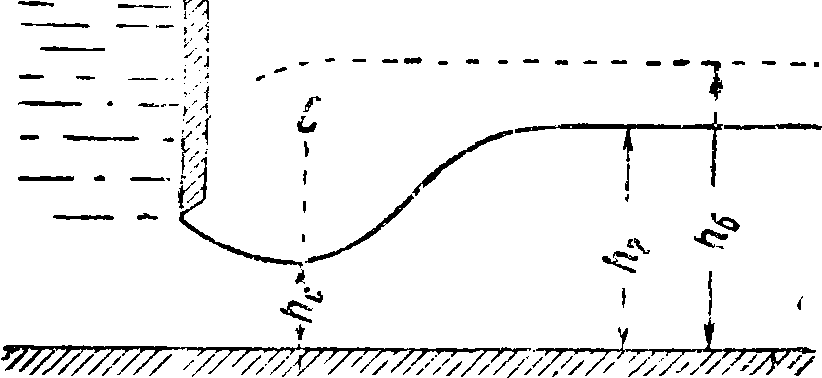
Разновидность случаев сопряжения кривых поверхностей воды в верхнем и нижнем бьефах выражается в наличии или отсутствии прыжка воды (смотрите). Наиболее опасен для сооружения отогнанный прыжок, зависящий от высоты h₂(фигура 1), наименьшее значение которой находится

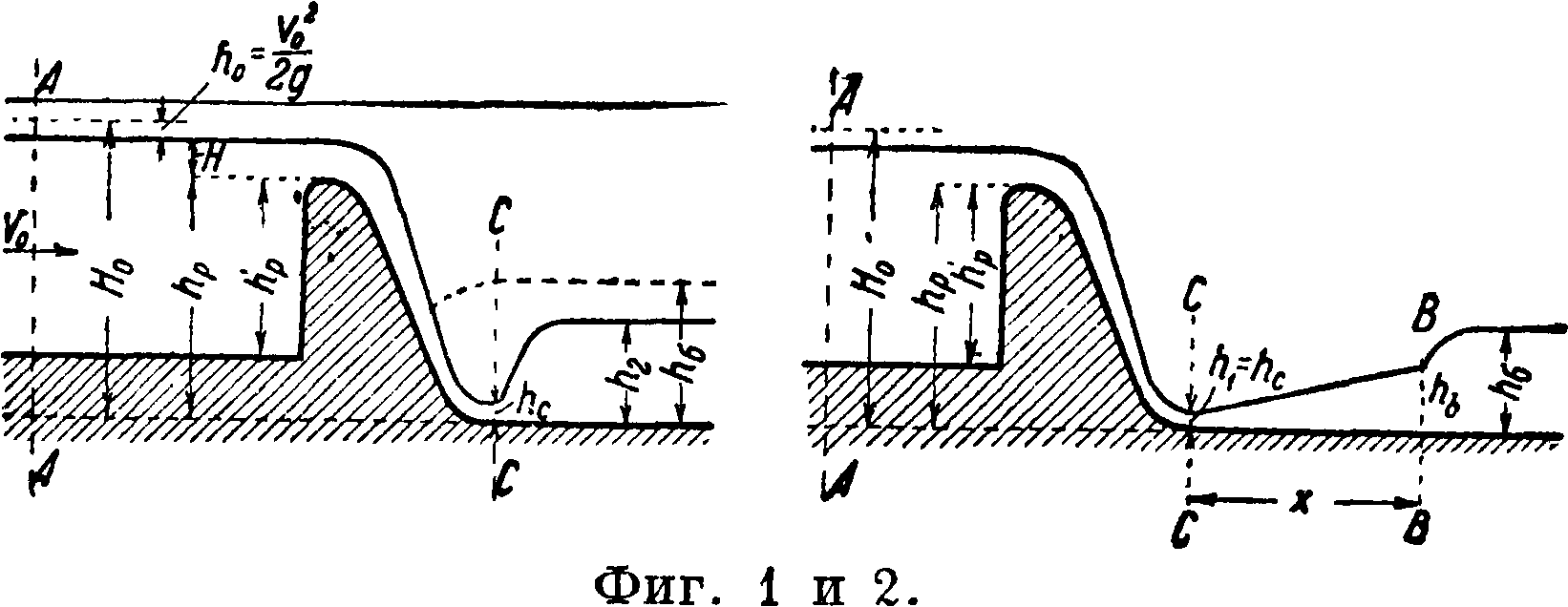
в зависимости от глубины h_c в сжатом сечении струи. Для определения величины h_e воспользуемся ур-ием Бернулли. Напишем это ур-ие для двух сечений АА и СС, тогда получим:

i + ^vi + w+h)=i + ^p-; + ^h+_hn

где v₀ — скорость подхода, v_c — средняя скорость в сжатом сечении, g — ускорение силы тяжести, р₀—р_с — атмосферное давление, γ — собственный вес воды, Н — напор над гребнем водослива, h_p — превышение гребня водослива над плоскостью сравнения, — потеря напора на пути от сечения АА до сечения СС. В этом ур-ии ♦

и где Q — расход жидкости, b — ширина потока поверху в рассматриваемом сечении, ζ — коэфи-циент местного сопротивления. Обозначив сумму /2

+ Н + hp) через Н₀ и заменив величины hf и v_c их значениями, получим;

^Я° ⁼ 26 + У + А

Т. к. (1 + ζ) — —, где φ — коэф. скорости, то

Hq — h_c +

2gvbZh%

Высота h₂ уровня воды при прыжке определится по взаимной ее глубине (смотрите Прыжок воды) из выражения:

причем max h₂ получится при min h_ί} то есть в наиболее сжатом сечении h_c. Зная величину h₂, можно по соотношению этой глубины с бытовой глубиной h₆ выявить форму струи при Б. с.; имея в виду, что при h₆ > h₂ прыжок отсутствует, получается т. н. затопленный прыжок, при h₆== h₂ имеем надвинутый прыжок, а при h₆ < h2 — отогнанный прыжок. По Базену во всех тех случаях, когда z : h₆ > 0,75, получается отогнанный прыжок, а когда z : h_p < 0,75, получается затопленный прыжок, то есть прыжок отсутствует. Величина z в данном случае означает разность уровней воды верхнего и нижнего бьефов (перепад). Бытовая глубина h₆ может быть определена по формуле для равномерного движения воды в канале:

h₆ —

Ь · со V #о“о где R₀ — гидравлич. радиус, i₀ — гидравлич. уклон, с₀ — коэф., равный по Маннингу по Форхгейму

Сп — — .R

Vo о >

со - 4- д

величина п представляет собою коэф. шероховатости по Гангилье и Куттеру.

Помимо высоты прыжка необходимо знать также длину отгона^ прыжка. Для этого находим такую длину х (фигура 2), при которой толщина струи возрастает до некоторой глубины h₆, взаимной с бытовой глубиной h₆. В этом случае величина h_e м. б. определена по ф-ле:

Для каналов же сравнительно небольшой ширины и достаточно глубоких с очертанием правильным, но сильно разнящимся от прямоугольного или параболического (например трапецоидаль-ное очертание), следует пользоваться уравнением Бахметева:

^х<)=V, — т ·

где

_ Cl + С2.

ъ„=h+J*·

2 ’

χ - - χ

χ— смоченный периметр; χ₀=—; Б (η)—ф-ия Бахметева:

экспонент а представляет со“5ой гидравлич. показатель русла; остальные величины имеют то же значение, что и в ур-ии Бресса. Длина х отгона прыжка получится поэтому по Бахме-теву равной:

-=^hi fЧ, - Vi-- ί¹ - °-ψ · Й[5Ы - БЫ])·

Для получения затопленного прыжка прибегают в соответствующих случаях к устройству водобойных колодцев, образуемых путем устройства особого углубления в дне канала или пууем возведения водобойной стенки. Потребность в таких устройствах является в тех случаях, когда данное сооружение обусловливает наличие прыжка, характеризуемого формой струи при Б. с. При отсутствии прыжка надобность в указанном углублении или стенке отпадает.

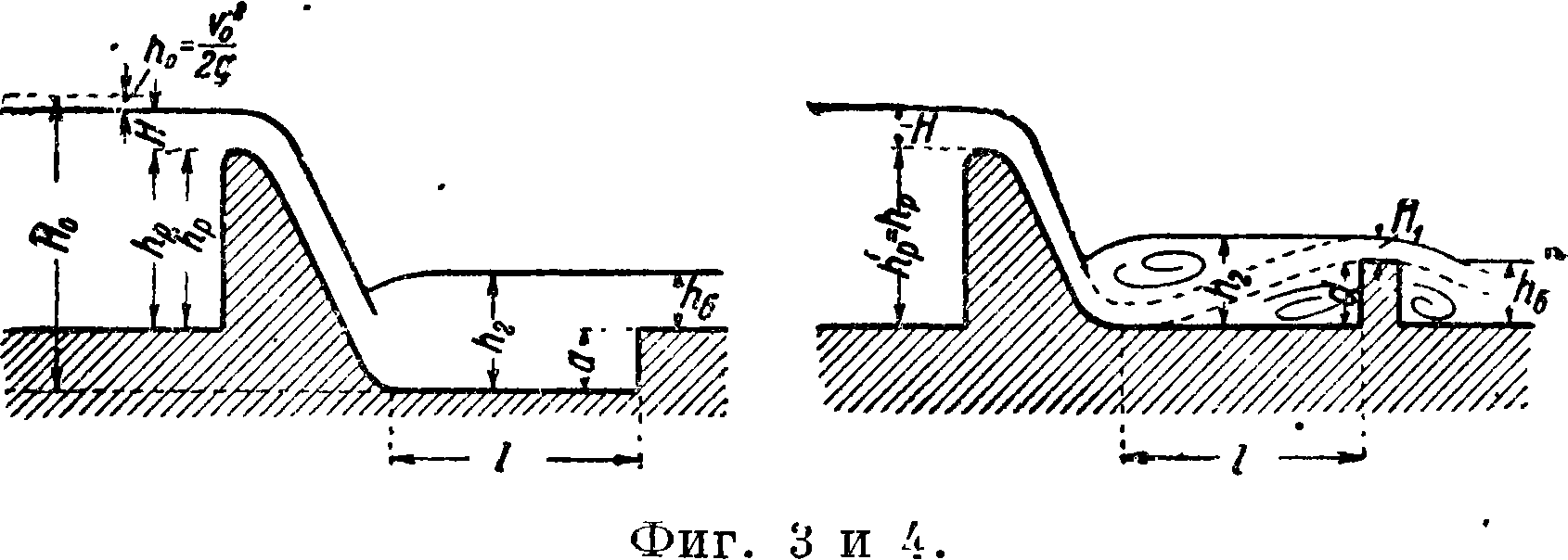
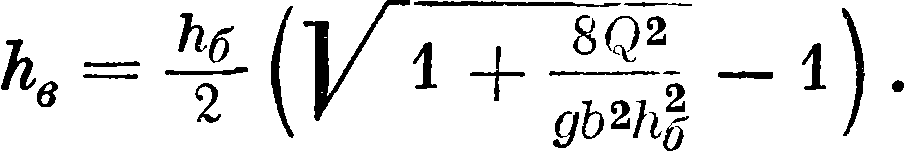
Для вычисления длины х отгона прыжка можно воспользоваться ур-ием Бресса, имеющим вид:

= ч. - Ч1 - (l - H±Jo) [φ [η,) - φ (,)},

где индекс «0» показывает, что речь идет о величинах при равномерном движении воды, а индексы «2» и «1» показывают, что величины относятся у. соответствующим двум сечениям канала. В данном случае величины г₀, с₀ и g имеют те же значения, что и выше; h₀=h₆ х₂ — х_г —

= х η₂ — ηι —^а — коэф., вводимый в ур-ие за счет вычисления количества движения по средней скорости; величина φ (η) представляет собой формулу Бресса, вычисленную последним для разных значений η. Величина х т. о. определится из выражения:

*= т_а{^щ ~ ^Vl — {^l ^ ~~ (Ч!)]} ·

Ур-ие Бресса применимо для широких прямоугольных и сравнительно неглубоких каналов.

При наличии йрыжка выясняют сначала форму струи при Б. с. и величины h_cmh₂, после чего приступают к гидравлич. расчету водобойного колодца, определяя его глубину а и длину I (фигура 3). Глубину а подбирают так, чтобы

h₂ — he -f- а.

Полученную теоретич. путем величину а увеличивают на 25%. Следовательно а — 1,25 (h₂ — h₆).

Высота водобойной стенки (фигура 4) определяется аналогичным образом из условия

h₂ — d + Н_1у

где толщина Н_г слоя воды, переливающейся через водобойную стенку, вычисляется по формуле водослива (смотрите). Для приближенного решения задачи по определению глубины водобойного колодца можно воспользоваться способом Базена, по которому прыжок отсутствует, если относительный перепад — <0,75, где z —

Ир разность уровней бьефов, h_p — возвышение гребня водослива над дном колодца. По Бахметеву следует, пользуясь способом Базена, учитывать также коэф. расхода m и отношение напора Н к высоте водослива с низовой его стороны λ_β·

Длина водобойного колодца Z, устраиваемого в особом углублении или образуемого стенкой, определяется по эмпирич. формулам, причем эта длина должен быть такова, чтобы было предотвращено выскакивание струи из колодца. По Блей

I — hp — hp -f- а.

По Этчеверри

I=1,5 Vz-h_p=1,5 z(h_p + aj

По Дейшу__

I ⁼ 1 »5 V(н + (hp + а).

По Журину

‘Z=l,6 yH(h_p + a+Ofiffl).

По Ребоку

I=^Ω -0,8α

где I — большая ось эллиптич. вальца, а — малая ось этого вальца, Ω — площадь эллиптич. сечения вальца, равная:

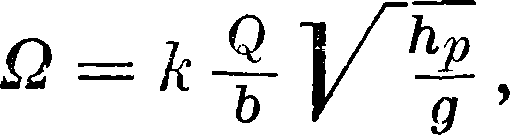
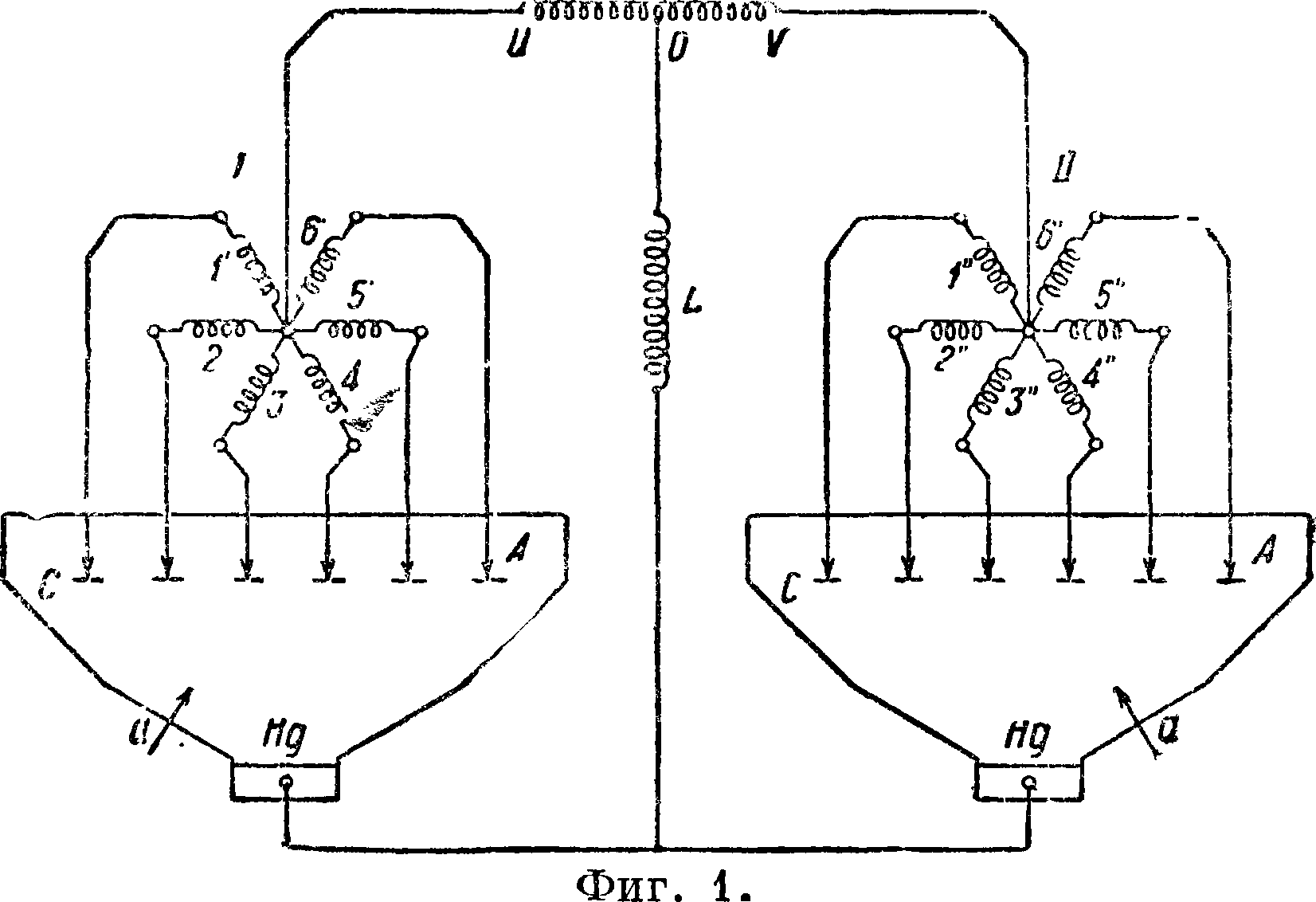
причем к=3,6 -У 7,2. Шоклич получил для своего водобойного колодца длину показаны два шестианодных выпрямителя с электрически соединенными катодами Нд (а — аноды возбуждения выпрямителя). Однако возможна и любая другая комбинация выпрямителей — 12 одноанодных, 6 двуханодных, 4 треханодных и наконец один двенадцатианодный

—ffff β ίΠΓΰϊΠϊ WOTCTi ffi ¹

l=(0,5 -7- 1,0)A

^Jp

Совершенно так же, как водобойные колодцы, рассчитываются и перепады (смотрите).

Указанные методы выявления формы

’ ₅ струи, длины .отгона

^иг* * прыжка и расчета во добойного колодца одинаково применимы как к струе, циспадающей с водослива, так и к струе, вытекающей из-под щита (фигура 5).

Лит.: Брилинг С., Механика твердых и жидких тел, Справочник для инженеров строительной специальности, М., 1928; Бахметев Б., О неравномерном движении жидкости в открытом русле, Л., 1928; Ев-реинов В., Гидравлика, Л., 1933; Павловский Н., Гидравлический прыжок как водомер, Л., 1931; Чарномский В., Задачи на установившееся неравномерное течение воды, СПБ, 1914; Павловский Н., О неравномерном движении при горизонтальном дне водотока, Л., 1930; его же, О неравномерном движении в водотоках с обратным уклоном дна, Л., 1931; Ах у тин А., Рабочая книга по специальному курсу гидравлики, М., 1931; его же., Примеры гидравлических расчетов в области неравномерного движения воды в открытых каналах, М., 1928; Ели-аз а р о в И., Гидроэлектрические силовые установки, Л., 1924; В г e s s e J., Cours de mecanique appliqu6e, 2 partie, Hydraulique, P., 1860; Tolkmitt G-., G-rund-lagen der Wasserbaukunst, B., 1907; Darcy H. et Bazin H., Recherches hydrauliques, P., 1865; Forch-hei me* Ph., Hydraulik, 3 Aufl.,*Lpz., 1930; Riihl· mann M., Hydromechanik, Hannover, 1880; R e libo c k Tb., Betrachtungen liber Abflusstau und Wal-zenbildung. B., 1917; Rehbock Th., Bekampfung der Soblenauskalkung bei Wehre durcb Zabnscbweller, «VDI», 1925, 44; Stevens J., «Engineering News

Record», N. Y., 1925, 14, 23; В a r i c 1 e, Nouvelle methode pour la d6termination des courbes de remous, «GC», 1921, 23, 24; Husted A., New Method of Computing Backwater and Drop-Down Curves, «Engineering News Record»; N. Y., 192Д. С. Брилинг.