> Техника, страница 28 > Векторное исчисление

Векторное исчисление

Векторное исчисление, отрасль математики, занимающаяся непосредственными вычислениями над направленными величинами. В. и. дает возможность гораздо проще и нагляднее выразить многие соотношения между физич. и даже чисто геометрии, величинами, чем это имеет место при вычислениях в координатах.

Величина, которая вполне определяется одним числен, заданием, называется скалярной величиной, или скаляром (она измеряется по одной шкале); если для определения величины необходимо еще указать ее направление, то такая величина называется вектором (например перемещение, скорость, сила). Геометрически вектор изображается при помощи направленного отрезка или стрелки Р,Р_г (фигура 1). Точка Р, называется началом, точка Р₂—концом вектора; —”°^г

расстояние Р_гР₂ определяет р, длину вектора. Векторы обо- _{фиг t}значают в печати при помощи жирных букв; длину вектора, или его абсолютную величину (модуль), обозначают помещая знак вектора между прямыми, черточками или же при помощи соответствующей нежирной буквы, например А или А обозначают длину вектора А. Иногда обозначают вектор, помещая над соответствующей буквой черточку или стрелку, например ω; этим обозначением пользуются преимущественно в рукописях. В Германии б. ч. обозначают векторы готич. буквами. Два вектора равны между собой, если они имеют одинаковое направление и одинаковую длину. Вектор равен нулю, если его начальная и конечная точка совпадают; в этом случае нельзя говорить о направлении вектора.

Чтобы сложить несколько векторов, их переставляют так, что к концу первого вектора приводят начало второго, к концу второго—начало третьего, и т. д. Вектор,

и

соединяющий начало первого вектора с концом последнего, называется векторной суммой данных векторов. Сложение векторов обозначается обыкновенным знаком +. Определенная т. о. векторная сумма не зависит от порядка слагаемых и вообще допускает все формальные преобразования, свойственные алгебраическ. сумме. При двух слагаемых это правило сложения тождественно правилу параллелограмма, по которому складываются скорости и силы (сложение векторов в пространстве впервые применил итальянец Bellavitis в 1838 г.). Вычитание векторов есть действие, обратное сложению. Можно, однако, определить вектор —В как вектор, равный по длине и противоположный по направлению вектору В. Тогда вычесть В значит прибавить —В, то есть А + (-В)= А-В.

Умножить вектор А на число λ значит получить новый вектор В, параллельный А и по длине равный |Я|А; если КО, то направления А и В противоположны. В В. и. различают два вида произведений векторов: скалярное и векторное. Скалярное произведение двух векторов есть число; оно равно произведению из длины одного вектора на проекцию второго в направлении первого. Для изображения скалярного произведения двух векторов пишут эти векторы рядом без всякого знака между ними: AB=AB cos а, где «—угол между А и В. Легко видеть, что скалярное произведение обладает переместительностью и распределительностью относительно суммы:

АВ =ВА, А(В + 0=АВ + АС.

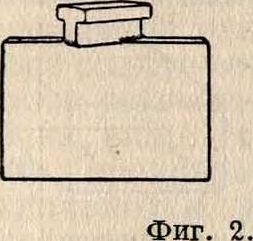
Во всех случаях — AB =£ АВ АВ. Если АВ=/=0. но АВ= 0, то AJ_B. По определению АА =А² =ЛА Квадрат вектора равен квадрату его длины. Если да²=1, то иг называется единичным вектором. Примером скалярного произведения является работа Т постоянной силы F, действующей под углом к, при перемещении» материальной точки: Т =Fs =Fs cos к. Другие обозначения скалярного произведения: (АВ),(А,В),(А-В). Векторное произведение двух векторов А и В есть вектор S, перпендикулярный плоскости АВ, направленный в сторону движения правого винта при вращении его от Л к U (правило штопора) и равный по длине площади параллелограма, построенного на А и В. Векторное произведение обозначается помещением сомножи-телей в квадратные скобки без какого-либо знака между ними (смотрите фигура 2): $=[-41>]==-[ВА] пои этом: S=АВ sin a; SA=О, SB=0; [А(В+С)]=[АВ]+[АС]. Векторное произведение обладает распределительностью относительно сложения, но оно а н-тикоммутативно, то есть меняет свой знак при перестановке сомножителей. Векторное произведение вектора самого на себя равно нулю: [4Д]=0. Другие обозначения для векторного произведения: (АхВ), (АЛВ), АВ, АВ, АВ. В произведении

А

Фигура 2.

нескольких векторов АВ-С озна чает вектор С, помноженный на скалярное произведение АВ; точка отделяет число АВ от вектора С, т. о. АВ С и А ВС—два совершенно различных вектора. Если помножить векторное произведение [АВ] скаляр-но на третий вектор С, то получается смешанное произведение:

[АВ]С =[ВС]А =[СА]В=-[СВ]А,

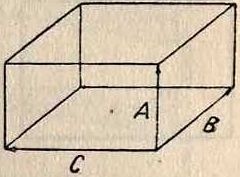
равное по абсолютной величине объёму параллелепипеда, построенного на векторах А, В, С (фигура 3). Это произведение обозначается иногда без скобок, просто: V=ABC. Если F>0, то векторы А, В, С образуют правую связку, [АВ] составляет острый угол с С. Если F<0, то А, В, С образуют левую связку. Если АВС=0, то А, В, С парад- фигура 3. лельны одной и той же плоскости —они компланарны. Всегда -АВС^АВС^АВС. Если АВС=АВС, то А, В, С взаимно перпендикулярны и образуют правую связку. При умножении вектори. произведения [АВ] векторно на С получится новый вектор

[[41В]С]=В АС—А ВС.

(Эта основная формула в первый раз была приведена Грасманом в 1862 г.) Если А, В, С взаимно перпендикулярны, то [[АВ]С]= 0. Из этих формул легко выводятся преобразования произведений из четырех векторов:

[АВ][СВ]=АС BD-AD ВС; [[АВ][СВ)]==С А В В - В А ВС=В А СВ-ABCD и тому подобное.

Деление векторов в обычном смысле невозможно, потому что одно скалярное или векторное произведение недостаточно определяет искомый вектор; например, если в равенстве Αν даны а и А, то

V=^5 А +[Ау] или V=где у—п р о и з-вольннй вектор. Если дано [να]=Α, тоν=^~-+να, где ν—произвольный скаляр. Для полного определения вектора должен быть три скалярных ур-ия: Αν=α; Βν=β; Cv=y; тогда v =aA’ + βΒ’+ yC’, где А’, В’, С’—три вектора, обратных (взаимных) данным векторам M,-В, С. Эти обратные векторы определяются формулами: _г, [СА] _г,

^Л ~ ЛВС ’ ЛВС ’ ^ ЛВС

и удовлетворяют поэтому таким соотношениям: АА’=ВВ’=СС’=1;АВС А’В’С’=1; АВ’=АС’=0 и т. д. Эти ф-лы позволяют разложить любой вектор А на составляющие по трем заданным направлениям, определяемым тремя единичными векторами т, п, р. Для этого образуем обратные векторы т’, п’, р’; тогда

А=Ат’-т + Ап’ η -+- Ар’ р. Следует заметить, что вместе с тем А=Ат-т’+ Ап-п’ + Ар-р’.

Если требуется разложить.4 на два составляющих вектора, параллельно и перпендикулярно единичному вектору п, то получается

А=п А п А п[А η]].

Разложение А на составляющие параллель-но р и перпендикулярно s дает (при ps Ф 0):

Лв [3[Ap]J ps ^ 2>8

А =р-

Для определения точки Р в пространстве относительно выбранной произвольно в пространстве точки О служит радиус-вектор г, который совпадает по величине и направлению с вектором ОР. В отличие от рассмотренных до сих пор векторов радиус-вектор зависит не только от положения конечной точки Р, но также и от положения начальной точки О. Уравнения, подчиняющие радиус-вектор определенным условиям, дают решение ряда задач геометрии и механики, например: (г·—i*j) А =0 есть ур-ие плоскости, проходящей через точку г₁ перпендикулярно к А; уравнение (г— г_г) [шп] =0 есть уравнение плоскости, проходящей через точку г_г параллельно тип·, [гп]—М{при м²=1) есть уравнение прямой,параллельной»»,проходящей от начала О на расстоянии М, причем плоскость, проходящая через О и через эту прямую, перпендикулярна к Ш. Если имеется ряд материальных точек Р₍, радиусы-векторы которых равны соответственно г_{, а массы т_{, то центр тяжести такой системы определяется радиусом-вектором

2m,r.

г= Если твердое тело вращается с уг-

2d

ловой скоростью (О вокруг оси, проходящей через начальную точку О в направлении единичного вектора п, то это вращение характеризуется вектором угловой скорости ω — от. Тогда линейная скорость V движения любой точки Р этого тела, радиус-вектор которой г, определяется поф-ле: v=[u>r]. Если на эту точку Р действует сила F, то момент этой силы относительно точки О равен вектору M—[rF], Следовательно, для того чтобы Ж оставалось постоянным, конец радиуса-вектора г, то есть точка приложения силы F, может перемещаться только параллельно F.

Для действительного численного задания вектора необходимо выбрать какую-либо систему координат, относительно которой определяется вектор, так как абсолютного направления в пространстве не существует. Выберем три взаимно перпендикулярных единичных вектора i 3 ,7с. паналлельных координатным осям ΟΧ, ΟΥ, OZ и образующих правую связку, ijJc=+l. Тогда г² —j²==к^%—, ij =j7c=Jci=0; [ij]=k, [j7c=i, [1ci =j. Теперь можно разложить любой вектор параллельно единич. векторам i, j, 7с: A —Ai-i + Aj-j + А7г 7с — А_хг +A_yj + AJt, где A_x=Ai, A_y=Aj, А_г=А7с—проекции, или координаты, вектора А. Равным образом:

Г>=В_хг - Byj + В_г7с- С=C_xi Р С_УЭ Р С_г7с.

Нетрудно видеть, что А +В={A_x+B_x)i+(A_y+By)j +(А_г+В;>7с-; АВ =А_ХВ_ХР АуВу- - ДгД_г; А^г=А£-{- Аур А%.

Два последних выражения определены геометрически независимо от выбора координатных осей, они сохраняют поэтому неизменное значение при вращении координатных осей, или, как говорят, они инваг риантны относительно вращения координатных осей. Далее можно вывести следующие соотношения:

[AB]=(A_J/B,—A_tB_v)i+(A_isB_x—A_xB_z)j+

+ (А_хВу—АуВ_х)7с =

г j к

Αχ Ay А.% В_х By B_z

Αχ Ay A_z

AB]C =

Cx Cy C_Z

I bX by

Эти формулы позволяют выражать векторные соотношения в координатах, и наоборот, например: Xa + Yb+Zc—скалярное произведение вектора с проекциями X, Y, Z на вектор с проекциями а,b, с.

Весьма важное значение имеют т. н. в ек-торфункции, ав особенности линейные векторфункции, выражающие один вектор линейной функцией другого. Такие функции встречаются в теории упругости, в гидродинамике, в теории векторных полей, в механике систем. Так, упругая сила В, действующая на единицу поверхности деформирован. тела, есть линейная векторфункция единич. нормального вектора п, перпендикулярного к площадке, на к-рую действует сила: Р —ni ia₁Anj· ja₂+пТс 7ca_s.

Такие векторфункции изучаются в аффи-норном, или тензорном исчислении (смотрите).

Векторный анализ. Функции скалярного параметра. Если данный вектор зависит от скалярного параметра, например от времени t, то для изучения этой функциональной зависимости сравнивают различные положения конца вектора при неподвижном начале. Когда t непрерывно изменяется, конец вектора A(t) описывает некоторую кривую (смотрите фигура 4). По определению, геометрическая производная вектора A(t) есть предел след, выражения

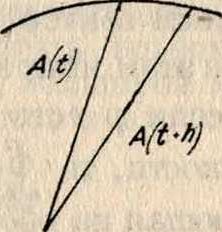
Фигура 4.

^ _{= Ит}^±^й.

^dt i=o ^h

Очевидно, что производная вектора постоянной длины перпендикулярна к этому вектору. Рассмотрим кривую, радиус-вектор всех точек которой г является функцией дуги кривой s. Тогда производная=где

t—единичный касательный вектор к кривой, описываемой концом г. Далее ^=кп, где А^кривизна кривой, а п—единич. вектор главной нормали. Векторы t и п, по определению, образуют соприкасающуюся плоскость кривой, а Ь =[*«]— единичный бинормальный вектор.

Можно также показать, что ~=—хп. где х —

скаляр; число х называют кручением кривой. Если радиус-вектор зависит от двух независимых скалярных переменных, то есть r=(u, ν), то конец этого вектора описывает поверхность. M, наконец, если радиус-вектор зависит от трех независимых скалярных переменных и, v, w, то конец г описывает часть пространства. Переменные u,v,w называются криволинейными координатами конца вектора г.

Т. Э. m. III.

и

Фигура 5.

lim 4- dS-V-o ^v J

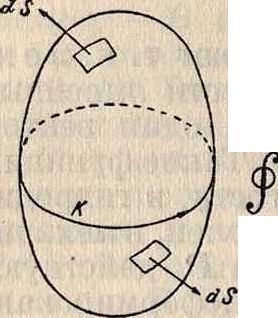
Скалярные и векторные поля. Если скаляр р имеет во всех точках нек-ро-го пространства определенные значения, то тогда это пространство является полем скаляра р. Для изучения изменения р в его поле необходимо знать, как будет изменяться р при перемещении в любом направлении из его начального положения. Для этого поступают следующим образом: ^окружают данную точку М„ оболочкой и разбивают эту оболочку на элементы поверхности dS, причем величина вектора dS равна площади dS, а направление определяется единичным вектором внешней нормали п 2) образуют для каждого элемента поверхности произведение pdS и вычисляют сумму этих произведений по всей оболочке

pdS; 3) делят на объём F,

заключенный внутри оболочки; 4) стягивают эту оболочку вокруг точки М_а т. о., чтобы объём V стремился к нулю (смотрите фигура 5). В пределе получается пространственная производная скалярной функции р, обозначаемая в виде

VP

V-0

ур — вектор,называемый также градиентом р. Проекция этого градиента на любое направление, характеризуемое единичным вектором т, равняется производной р др в этом направлении: т р= например, если р есть давление в любой точке жидкости, то j>pdS—сила давления, действующая на оболочку, окружающую точку М„. Тогда -~Y^pdS есть средняя сила, действующая на единицу объёма внутри оболочки, а —ур есть сила, действующая на единицу объёма в точке М₀. Вместо р иногда применяют обозначение gradp.

Пространственные производные в векторных полях образуются точно таким же образом. Если имеется поле вектора А, то, по определению, потоком вектора А через оболочку, окружающую точку М₀,

называется выражение <j)A dS. (Если бы А изображало в каждой точке скорость движения жидкости, то j>A dS равнялся бы объёму жидкости, вытекающей в единицу времени через оболочку.) Разделив на объём и переходя к пределу (F=0), получаем поток на единицу объёма в точке М_а, называемый дивергенцией вектора А. Обозначение: div.4 или у4=lim ±£а dS. у=о ^v J

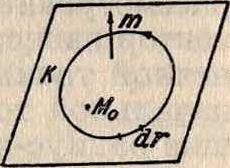
Так, если v изображает в каждой точке скорость движения несжимаемой жидкости, то поток вектора v через любую замкнутую поверхность равен нулю, поэтому div«=0. Если в интеграле по оболочке заменить скалярное произведение A dS векторным, то получится новая пространствен ная производная, называемая ротором вектора А. Эта пространственная производная есть вектор, обозначаемый следующим образом: rot A=[yA]= im~j)[A dS] (иногда применяется и такое обозначение: curl А). Проведем через точку Ж„ плоскость, перпендикулярную к единичному вектору т (смотрите фигура 6). Окружим точку М₀ замкнутой линией к. Разобьем контур к на элементы dr, направление которых связано с вектором т по правилу штопора, и образуем для каждого элемента скалярное произведение Adr.

Если бы вектор А изображал силу, то A dr было бы элементарной работой. Сумма произведений вида A dr, взятая по всему контуру, называется циркуляцией вектора А, или линейным интегралом <^А dr. Если разделить циркуляцию вектора А на площадь S, окаймленную контуром к, то для бесконечно малой площади S мы имеем:

ФИГ. 6.

if

A dr=т rot А.

Проекция ротора 4 на нормаль к данной плоскости равна циркуляции вектора А в этой плоскости, деленной на окаймленную площадь. Так, в электростатическ. поле циркуляция вектора электрич. поля JE равна нулю для любого контура. Поэтому в электростатич. поле_ rot 23=0. Пространственную производную вектора А можно также образовать и при помощи постоянного единичного вектора ш:

’mdS-A.

m у· Л =

= lim 4- <£г

v=o ^v J

Этот вектор равен производной вектора А в направлении т. Пользуясь символом у, видим, что для обозначения любой пространственной производной при помощи интеграла по оболочке надо написать подинтегральное выражение, заменив в нем вектор dS символом у; этот символ называют «набла» или дифференциальным оператором Гамильтона. Если выражать пространственные производные в декартовых координатах, то дифференциальный оператор Гамильтона м. б. изображен в виде символического множителя:

. а, а ,. а v =·αг + ³ Ту + ^к аГ

Таким образом W=* А =

до дх дА_х

дх

^{r J} ду

,^aAi

ду

. дА_г

+ Ж’

1 А] =

i	1	Тс
д	д	д
дх	ду	дг
Ах	Ау	Аг

дЛ

дЛ

и Т. Д.

дЛ

ту л=η±=+ ш_у ~ + т_г^

Применение векторных ф-л значительно облегчает понимание различ. преобразований; например помещенные в т. I Технической Энциклопедии в ст. Аэродинамика, ст. 829,

три уравнения (где X, Y, Z — проекции вектора силы F; и, v, w—проекции вектора скорости v) могут быть записаны в векториальной форме в виде:

1 ΎΧ 0®

-ур=p-vy-v- _w

а четвертое уравнение примет вид:

fi + v (е“0=о.

Ур-ия ст. 830 той же статьи, где ξ, η, ζ— проекции вектора ¹/₂ rot v, запишутся в виде:

F —“ УР — V^^{2 =} [rot ν·ν}.

С дифференциальным оператором у можно обращаться, как с вектором, если соблюдать нек-рые предосторожности (например различать величины, подвергаемые действию оператора ν> ^от величин, не подвергаемых этому действию). Тогда легко получить целый ряд полезн. преобразований, например: ν(φψ)=φνψ+Ψν^;

у-АВ=Ау-В+Ву-А+[А rotB]+[J3rot4]; y<pA=<pyA + Aysp;

ν[1Β]=B[yA]—A[yB]—B rot A—A rot B.

Последнюю формулу можно записатьитак: divUB]=([_V4])B - (L_VB])4; здесь кругл, скобки ограничивают действие операторау. Действие дифференциального оператора не распространяется через круглые скобки; например, скаляр

{Су-А)В=А(ВуВ)-В(Су-А) равен скалярному произведению из вектора В на производную А в направлении С, помноженную на С. Вектор

(у-4)В= By·А +[В rot А] градиент скалярного произведения АВ, в котором В считается постоянным. Поэтому надо считать неправильными обозначения вида (Ау)В и заменять их выражениями АуВ, а также (4Lgrad)B или [A grad] В, где символ grad стоит вместо у. Символ grad должен применяться только как сокращение слова «градиент» в применении к скалярным функциям.

Приведем примеры некоторых пространственных производных. Если г—радиус вектор, а с—постоянный единичный вектор, то

grad г=у, div ~=-|·; rot г=0; div(c-rc)=t; grad(cr)=c;

rot[cr]=2c; divr=3; cy-r—c; grad f(r)=f (r)

[[ с V1 *"] =-2c.

Дифференцируя пространственные производные, получаем вторые производные, например

div grad <р=уу<р=у^г<р.

Символ у² называется дифференциальным оператором Лапласа и в декартовых координатах выражается так:

₈ _ а“ э· а⁸

Ч ~ дх· ⁺ 0у“ + 02^s

Далее:

rot grad φ=[w] Ψ=0.

Вторыми производными от вектора будут: grad div А=у-уА; div rot А=[w]4L=0;

уу-4=V²^=grad div .4 — rot rot A.

В более сложных случаях можно при по мощи индекса при у обозначать тот вектор или скаляр, на к-рый действует дифференциальный оператор, например:

у АВ) =Ау²В +Ву²А+у_лу_в-АВ. Здесь у_л действует только на h, а у_в— только на В. Можно также для выделения величины, не подвергающейся дифференцированию, снабжать ее подстрочным знаком Т (комец), например:

пу-(ту-А)=ту-{пу-А). т т

Вычислим некоторые вторые производные:

у^гг=^_г; уЬ^л =6; у²гР=р(р+ 1)г^р~²; у² In г=~

Среди функций, удовлетворяющих уравнению v²<p=0, отметим функции:

In I cr] I; In (г + г),

где ζ и г—цилиндрич. координаты, <р—азимут. Если на нек-рых поверхностях в поле скалярных или векторных величин происходят резкие изменения этих величин, то тогда рассматривают поверхностные производные этих величин. Если п обозначает единичный вектор, нормальный к поверхности разрыва, а индексы 2 и 1 отмечают значения величин φ и А по обе стороны поверхности разрыва, то получается: поверхностный градиент Grad<p== n(<p₂—<pj); поверхностная дивергенция Div А — п(А₂—А₁); поверхностный ротор Rot А — [п(А_г—А·^]. Можно показать, что поверхностные производные являются пределом соответствующих пространственных производных; например, если считать поверхность разрыва пределом слоя, толщиной h, то произведение h div А стремится к поверхностной дивергенции:

lim h div А=Div А, при h, стремящемся к 0.

Кроме дифференциальных формул, не менее важны интегральные формулы. Следует отметить теорему Гауса, связывающую поток вектора А через замкнутую поверхность с объёмным интегралом его дивергенции, распространенным по объёму, заключенному внутри этой оболочки

<j> AdS =J div A άτ; в частности:

j)dr=0; (j) dS у-A=J* у² A dx; ^rdS — 3V;

(j>B-AdS — J (By-A + A div B) άτ.

Циркуляция вектора А, по теореме Стокса, равна потоку ротора этого вектора через любую поверхность, окаймлен, этим контуром:

j) Adr=J* rot A dS;

в частности:

^)grad φ dr=0; ^ dr=0; j) φ dr=J [dS grad <p ;

£ [drA]=f [dSy]A].

J k J S

Эти формулы чрезвычайно полезны при разрешении задач из области теории поля,

*14

теории потенциала, дифференциальн. геометрии и т. д. Так, если в поле вектора А обозначить его направление при помощи единичного вектора t, так что A=At, то этот вектор t будет касательным к силовым линиям, дифференциальное уравнение к-рых: [Adr]= 0. Если существуют ортогональные поверхности, пересекающие под прямым углом все силовые линии, то вектор t есть единичный нормальный вектор этих поверхностей. Тогда divi=.ZT, где Н в каждой точке равно средней кривизне ортогональной поверхности. Далее rot t=lcb, где к— кривизна, а b—бинормаль силовой линии. Пространственные производные вектора А равны в этом случае:

diV А= АН + tyA; rot A=Akb—[tgrad А].

В частности, если вектор А удовлетворяет условиям: div А =0, rot А =0, то его длина А удовлетворяет дифференциальным ур-иям

1 дА _ τι. 1 SA _ ί

A dt ~ A дп ~ ^К’

где ^ и ^ обозначают производные скаляра А в направлении t и главной нормали п; у^гЛ= —2К, где К—полная гаусова кривизна ортогональной поверхности. Эти формулы весьма полезны для исследования полей, удовлетворяющих дифференциальному уравнению Лапласа.

Векторный анализ является незаменимым орудием для изучения и исследования векторных полей, дифференциальных свойств кривых и поверхностей, гидродинамики, аэродинамики, теории упругости и тому подобное. Однако полного развития этот метод достигает только при одновременном пользовании тензорным (диадным, аффинорным) анализом.

Лит.: Френкель Я. И., Курс векторного исчисления, Л., 1925; Черданцев И.А., Основы векторного и тензорного анализа, 2 издание, Москва—Л., 1925; Шпильрейн Я. Н., Векторное исчисление, М.—Л., 1925; Ignatowsky W., Die Vektoranalysis und ihre Anwendungen in d. theo-retischen Physik, B. 1—2, Lpz., 1926; SpielreinI, Lehrbuch der Vektorrechnung, 2 Auflage, Stuttgart, 1926; G-a n s R., Eintiihrung in die Vektoranalysis mit Anwendungen auf die mathematische Physik, Leipzig, 1923. Я. Шпильрейн.