> Техника, страница 28 > Векторные диаграммы

Векторные диаграммы

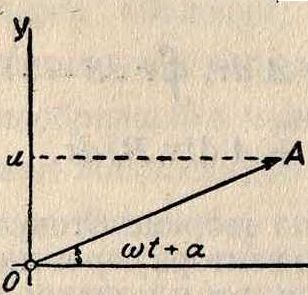
Векторные диаграммы, графическое изображение периодич. величин при помощи векторов. Чтобы изобразить колебание у=A sin (ιοί + а), откладывают в плоскости XOY под углом (ωί + а) от-^х резок, равный амп-ф_ИГ. i. литуде колебания:

О А =А (смотрите фигура 1). Когда время ί растет, этот отрезок вращается с постоянной угловой скоростью <в, и его проекция Оа на ось OY равняется мгновенному значению колебания:

Оα= A sin (ωί + а)=у.

Когда приходится сравнивать несколько простых колебаний одного периода, удобнее изображать их неподвижными векторами. Пусть, например, имеются колебания: y=As nwt, z=jBsin(a>i—а).

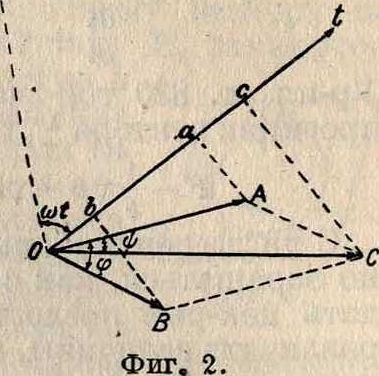
Тогда откладывают в любом направлении отрезок О А=А и отстающий от него на угол ψ отрезок ОВ=В (фигура 2). Для получения мгновенных значений этих колебаний проектируют векторы ОА, ОВ на прямую Ot, вращающуюся в отрицательном направлении с той же скоростью ω (ось времени). Здесь фаза колебания у принята за начало фаз (у=0 при ί„=0).

Ось времени занимает при ί_ο=0 положение OTj_OA и в любой момент времени ί составляет с ОТ в отрицательн. направлении угол ωί. Тогда проекции Оа, Оb векторов О А, ОВ на ось Ot равняются заданным колебаниям: Оа=у, Ob=z. Сумма этих двух колебаний х — у + z=A sin ωί + В sin(a>i—φ)

изображается геометрической суммой ОС векторов ОА и ОВ. Это результирующее колебание х имеет амплитуду С=ОС и отстает от колебания у на угол ψ=АОС. Мы определили т. о. графически колебание х=С sin (ωί—φ).

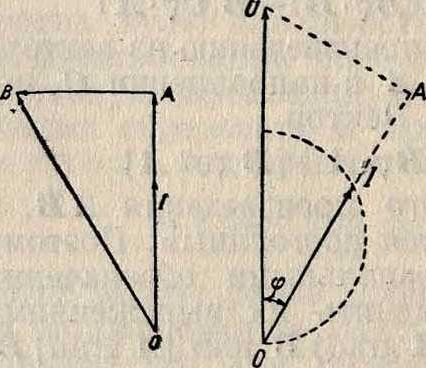
В. д. применяются в акустике, оптике и особенно в электротехнике. Построим, например, В. д. элек-трич. напряжения на зажимах дроссельной катушки с сопротивлением R и индуктивностью L, через которую проходит данный ток силы i =/sin ωί. Отложим вектор ΟΙ=1 (фигура 3). Тогда напряжение катушки разлагается на активную составляющую, равную OA—RI, и реактивную составляю-

Фигура з.

Фигура 4.

щую АВ=ΣωΙ, опережающую ток на ·

Когда изменяется индуктивность L катушки при неизменном сопротивлении R, то конец В вектора ОВ, изображающего напряжение, описывает полупрямую АВ. Это и есть В. д. напряжений, дающая при заданной силе тока амплитуду и фазу напряжения в функции от L. Нетрудно построить соответствующую В. д. тока. При заданном напряжении и=ZJsincai

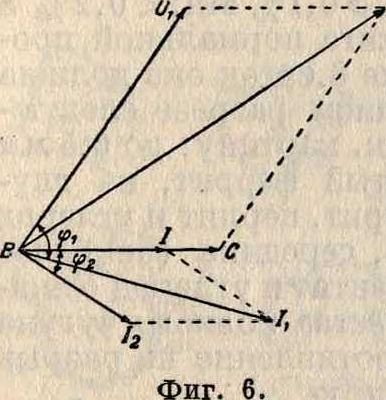
сила тока i изображается вектором 01, конец которого перемещается по полуокружности при изменении L (соответствующее омическ. падение напряжения Ш= О А и угол при А—прямой, опирающийся на OU; см. фигура 4). Эта В. д. также м. б. получена из диаграммы напряжения путем инверсии (смотрите). В. д. может также применяться для графического решения задач переменного тока. Пусть, например (фигура 5), переменное напряжение и включено на дроссельную катушку АВ с сопротивлением г_г и индуктивностью Σχ, соединенную последовательно с катушкой ВС

сопротивления г_г и индуктивности?Ь_г, шунтированной чистым омич, сопротивлением R. Возьмем произвольно отрезок BC=U₂, рав-

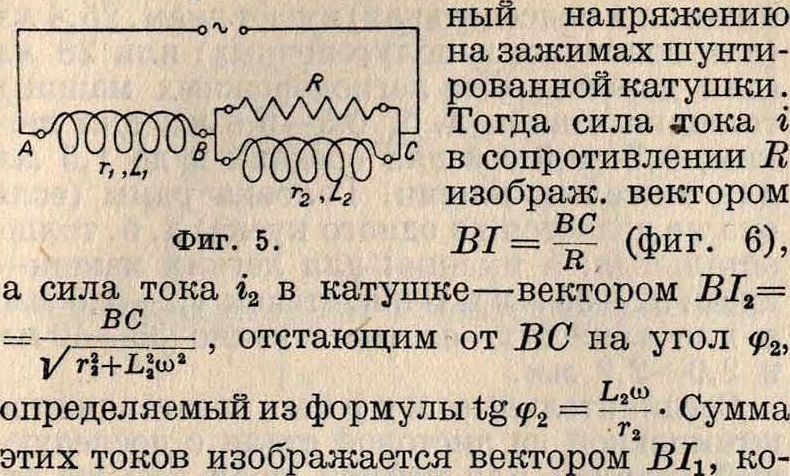
торый изображает также ток проходящий в катушке АВ. По этому току построим вектор напряжения на зажимах A-В, равный BU₁=h J/V;+£>² и опережающий В1_±на угол <p_lt определяемый из ф-лы tg ψ_χ=

= —^· Сумма напряжений АВ и ВС изобра-

жается геометрич. суммой векторов BJJ₁ и ВС и должна равняться заданному напряжению. Отсюда определяется масштаб всей В. д., а следовательно, и все токи и напряжения в отдельных частях схемы. В. д. могут

применяться и для несинусоидальных периодических величин путем замены их эквивалентными синусоидальными величинами (смотрите Переменные токи).

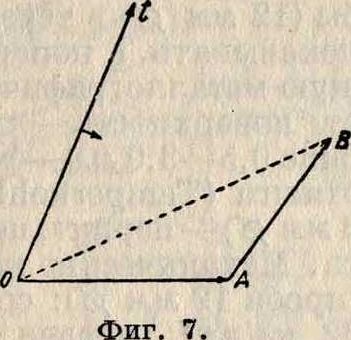
Наконец, В. д. могут применяться для сложения колебаний различной частоты, причем в этом случае векторы, изображающие отдельные колебания, не остаются неподвижными. Если ось времени Ot (фигура 7) вращается со скоростью а>, соответствующей частоте колебания О A sin a>t, то вектор АВ, изображающий колебание АВ sin ω_αί, должен вращаться навстречу оси времени с угловой скоростью ω_χ—οι. В этом случае результирующее непериодическое колебание О A sin u>t + АВ sin a_xt

изображается проекцией на ось времени вектора ОВ. В. д. применяются также для изображения затухающих колебаний.

Лит.: Круг К. А., Основы электротехники, М., 1926: Чердандев И. А., Теория переменных токов, М.—Л., 1924. Я. Шпипьрейн.