> Техника, страница 28 > Веревочный многоугольник

Веревочный многоугольник

Веревочный многоугольник (Вари н ь о н a) имеет большое применение в графических расчетах. При помощи его решают все задачи, относящиеся к равновесию сил на плоскости, проводят построения деформаций систем и т.д. Когда к точке А

приложено несколько сил 1,2,3, 4 (фигура 1, А), то равнодействующую этих сил получим, если мы найдем сначала равнодействующую i?! сил 1 и 2, затем сложим ее с силой 3 и, получив тем же способом равнодействующую сил Е_х и 3, равную R₂, сложим ее с силой 4.

Фигура 1.

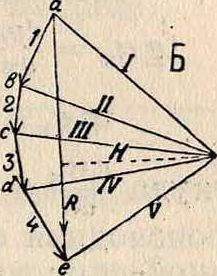
Последняя равнодействующая R и будет равнодействующей всех данных сил. К тому же результату придем, если данные силы 1,2, 3 и 4 последовательно перенесем в плоскости параллельно самим себе и составим из них мн-к abcde (фигура 1, Б), в котором стрелки сил по его периметру были бы направлены в одну сторон у—по направлению движения часовой стрелки или противоположно ему. Тогда вектор ае, соединяющий начальную и конечную точки такого многоугольника сил (называемого силовым мн-ком, или планом сил), представит собой искомую равнодействующую R по ее величине и направлению. Порядок, в котором соединяются данные силы при построении мн-ка сил, не имеет влияния на окончательный результат: при любом порядке собирания сил получаем ту же по величине и направлению равнодействующую. Если силы, приложенные к точке А, образуют в плане сил замкнутый мн-к, то равнодействующая ихЛ=0, и силы взаимно уравновешиваются. Когда данные силы приложены к различным точкам плоскости и не имеют общей точки пересечения, то определение равнодействующей этих сил можно сделать путем последовательного сложения их по правилу параллело-грама, как показано на фигуре 2. Но этот

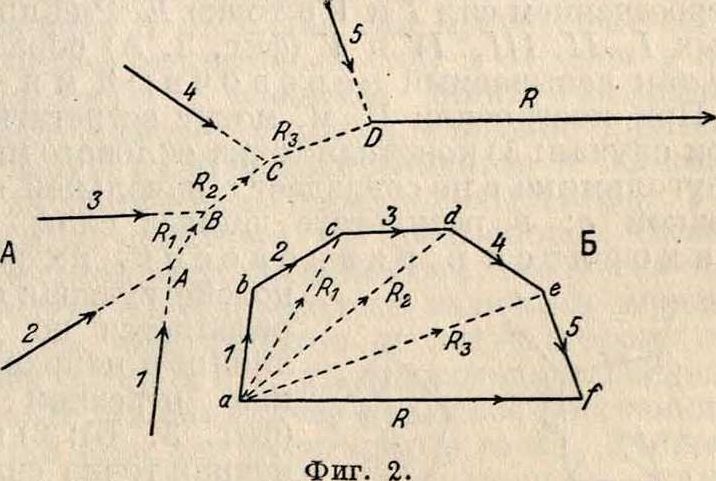
способ оказывается неудобным для определения положения равнодействующей, если силы пересекаются под очень острыми углами или вне пределов чертежа, и вовсе неприменим, когда силы параллельны между собой. ди в дм.; крутка на 1" равна где —

Фигура 9.

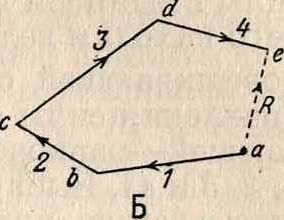
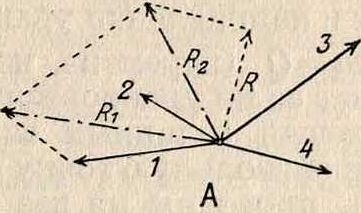
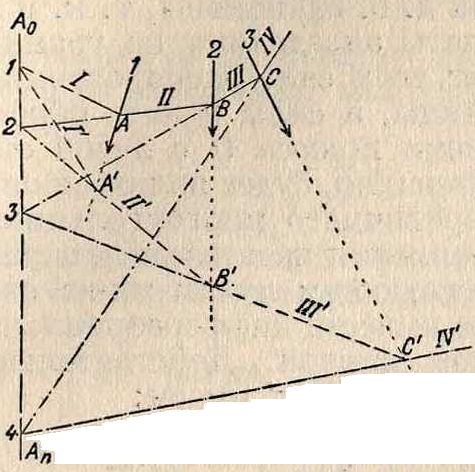
Самым общим приемом сложения сил является сложение их при помощи построения В. м. Пусть даны силы 1,2, 3 и 4, приложенные к разным точкам плоскости (фигура 3, А). Требуется найти величину и положение уравновешивающей Q этих сил. Данные силы соединяем в мн-к сил (фигура 3, Б) и из него находим величину и направление уравновешивающей силы ea=Q (перемена направления силы Q делает ее из уравновешивающей—равнодействующей заданных сил 1,2, 3 и 4). Выбираем произвольную точку О (называемую полюсом), проводим из нее к вершинам мн-ка сил лучи Оа, Оb, Ос,. и строим мн-к I, II, III, IV и V (фигура 3, А), начиная от произвольной точки А по направлению силы 1, т. о., чтобы одноименные прямые на фигуре 3,Б (план сил) и на фигуре 3, А (поле сил) были между собой параллельны.

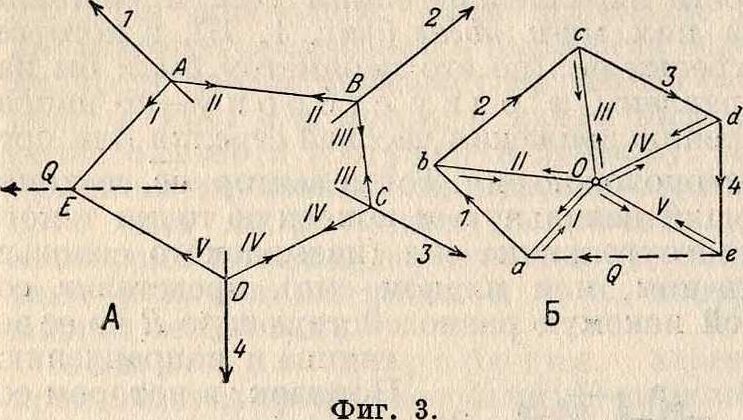
Прямые I, II, III, IV и V на фигуре 3, Б (называемые полюсными лучами) можно рассматривать как силы, которые уравновешивают данные силы. Так, из рассмотрения замкнутого тр-ка сил Оаb (фигура 3, Б) следует, что силы Оа и Оb уравновешивают силу 1. Точно так же Оb и Ос уравновешивают силу 2, и т. д. Тогда, взамен нахождения положения уравновешивающей силы Q заданных сил, можно отыскивать положение равнодействующей тех сил, которые уравновешивают заданные силы, что, очевидно, одно и то же. Но силы II и II у точек Αν. В, а также силы III и III у точек Б и С и силы IV и IV у точек С и D, взаимно уничтожают друг друга (фигура 3, А). Остается, т. о., найти равнодействующую сил I и V, приложенных к точкам А и В. Эта равнодействующая, по положению, определяется пересечением сил I и V в точке Е. Ряд прямых I, II, III, IV и V (фигура 3, А) образует так называемый веревочный мн-к.

При построении В. м. могут встретиться три случая: 1) конечная точка силового многоугольника е не совпадает с начальной его точкой а; в результате данные силы н е находятся в равновесии, их равнодействующая определяется по величине и направлению отрезком еа (фигура 3, Б); 2) конечная точка силового мн-ка совпадает с начальной его точкой, и крайние стороны В. м. параллельны между собой; в результате данные силы приводятся к паре сил, как по

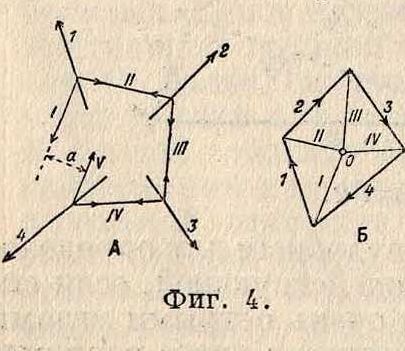
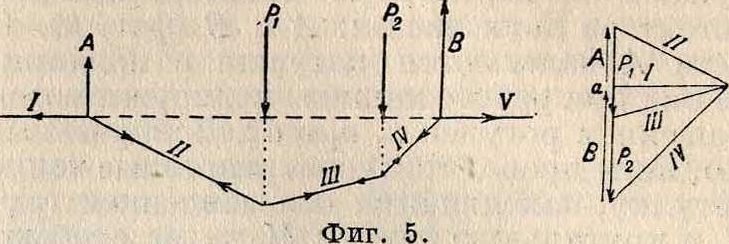
казано на фигуре 4, где а есть плечо пары, а произведение 1а или Va=M—момент этой пары; 3) конечная точка силового мн-ка а совпадает с начальной его точкой, и крайние стороны В. м. (I и V) совпадают между

t

собой (силовой и веревочный мн-ки сами собой замыкаются); в результате получается равновесие системы (фигура 5).

При помощи веревочного мн-ка задача о разложении заданной силы Р (фигура 6) на две параллельные ей составляющие Αν В, данные по своему положению, решается просто. Отложив в плане сил силу Р, выбрав произвольно полюс О и проведя лучи I и III, проводим их и в поле сил, начав с произвольной точки S на направлении силы Р. Прямая АВ даст /> тогда направление второго луча, при помощи которого, проведя из полюса О прямую OS, параллельную АВ, разделим заданную силу Р на две искомые составляющие Αν В. Подобным же образом можно решить и обратную задачу, встречающуюся при определении реакций опор балок: найти две параллельные, данные по положению силы А и В, которые находились бы в равновесии с двумя другими данными параллельными силами Pj и Р_г (фигура 7). Строим для этих сил план сил, берем точку О за полюс и строим В. м., начав его со второго луча на

И

Фигура 6.

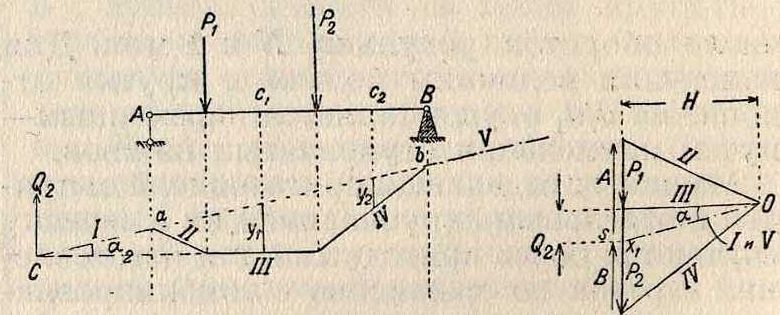
Фигура 7.

направлении реакции А. Так как при равновесии В. м., равно как и силовой, должны быть замкнутыми, то искомые лучи I и V должны сливаться, а потому направление их определяется направлением замыкающей прямой аb. Проведя из полюса О прямую Os, параллельную аb, определяем реакцию А (как отрезок между лучами I и II) и реакцию В (как отрезок между лучами IV и V).

В. м. обладает тремя степенями свободы при своем построении, так как полюс О выбирается произвольно (то есть произвольными являются две координаты, для полюса—две степени); кроме того в поле сил построение В. м. начинается с любой точки на заданном направлении 1-й силы (еще одна степень свободы), изменение полюса влечет за собой изменение контура В. м., но все они будут связаны тем условием, что точки пересечения одноименных сторон В. м. (фигура8), построенных для одной и той же группы сил, но при различных полюсах, лежат на одной прямой А₀А_п (называемой полярной

I

Фигура 8.

осью), параллельной оси 0_Х0₂—линии, соединяющей полюсы. Это непосредственно следует из того, что в любом четырехугольнике 2ВВ3 в поле сил и в соответствующем ему четырехугольнике b0_х0₂с в плане сил три стороны, образующие его, и две диагонали взаимно параллельны, следовательно четвертые стороны 2—3 и О_х—0₂ также параллельны; а т. к. отрезки 1—2, 2—3, 3—4 имеют общие точки, то прямая А₀А_п || О_хО_г. Наличие трех степеней свободы дает возможность обусловливать построение В. м. любыми тремя (и менее) условиями. Примером может служить проведение В. м. через три заданные точки. На фигуре 9 дано такое построение для группы сил Р_ь ., Р_в, с условием, что первый луч должен пройти через точку а, последний—через точку b, а луч 4, между силами Р_а и Р₄, через точку с. Сначала выбираем полюс О произвольно, строим

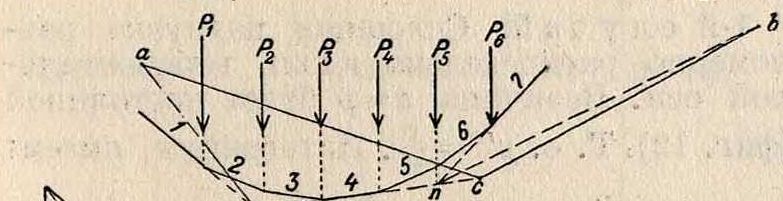
Фигура 9.

1-й В. м. 1-2-3-4-5-6-7, начав построение с точки е, проведя через нее луч 4; затем строим влево лучи 3, 2, 1 и вправо лучи 5, 6 и 7. Точками кип определяются положения равнодействующих R_x (сил Р_г, Р₂и Р₃) и Р₂ (сил Р₄, Р₅ и Р₆). Проведя луч ак, мы тем самым заставим левую сторону мн-ка пройти через точки а и с. Этому мн-ку будет соответствовать новый полюс d. Аналогично лучом bп в правой части определяется мн-к, проходящий через точки с и b. Этому мн-ку соответствует новый полюс e. Т. к. по условию левые мн-ки своими крайними сторонами должны проходить через точки а

и с а все правые через точки с и b, то новый полюс 0_1; удовлетворяющий условию прохождения общего мн-ка через точки а, с и 6, определяется пересечением прямых dO_x |[ ас и еО_хIIbс. При этом полюсе В. м. пройдет через все три заданные точки, и, так как все три степени свободы В. м. здесь использованы, построенный В. м. будет единственно возможным. Если за полюс принять начальную точку силового многоугольника а, то каждая из сторон В. м. R_t, Р₂ и т. д. (фигура 2) дает положение и направление равнодействующих всех сил, предшествующих рассматриваемой стороне. Последи, сторона совпадает с равнодействующей всех отдельных сил (применение—кривая давления).

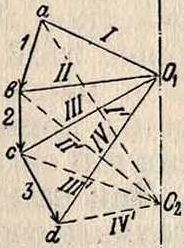
При помощи В. м. определяются статические моменты сил и грузов относительно любой точки плоскости. Пусть даны силы 1, 2, 3 и 4 и требуется найти их момент относительно заданной точки С (фигура 10, А). Соединим данные силы в мн-ке сил и построим для них В. м. Проведем через точку С

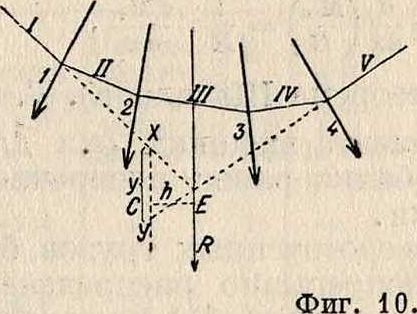
прямую, параллельную R, и назовем через у величину отрезка ее между направлением крайних сторон В. м., а через Н—расстояние равнодействующей В от полюса О (называемое полюсным расстоянием). Сравнивая два подобные тр-ка ЕХУ и Оае и принимая во внимание, что момент составляющих сил равен моменту равнодействующей, можем написать: R:H=y:Ji, откуда Rh== М=Ну,т.е. статич. момент данных сил равен произведению полюсного расстояния Н и их равнодействующей на величину отрезка у, отделяемого крайними сторонами В. м. на прямой, проведенной через заданную точку С параллельно R. Знак момента определяется по направлению вращения R относительно точки С. Следует заметить,что величина Н из плана сил прочитывается в масштабе отложенных сил, а отрезок у из поля сил — в масштабе длин. У казанное свойство имеет большое приложение для вычисления изгибающих моментов в балках, когда данные силы параллельны. На фигуре 7— свободно лежащая на двух опор_ах балка с системой параллельных сил; требуется определить последовательно величины моментов сил, находящихся по левую сторону от точек C₁, с₂, с₃ и т. д., относительно последних. В данном случае полюсное расстояние Н для всех сил будет одно и тоже. Данные силы A, Pi, Р₂, В откладываем в плане сил и строим В. м. I-II-II1-IV. Затем, по предыдущему, проводим через точку с_х прямую, параллельную равнодействующей, которая вертикальна, и находим отрезок г/, между крайними сторонами I и III. Тогда произведение Jlij =у₁Н выразит искомую величину момента всех сил, лежащих левее точки Су. Аналогично для второй точки, с₂, М_г=у₂Н, и т. д. Т. о., искомые значения моментов оказываются пропорциональными ординатам у сторон В. м. относительно первой стороны его и, следовательно, изменяются между двумя смежными силами по закону прямой. Величина равноAeftcTBV-ющей Q сил на участке между силами Р_г и Р₂определяется в плане сил отрезком, заключенным между Iи III лучами, и равна Q₂==А—Ру. Ее положение определяется в поле сил точкой С пересечения лучей I и III (фигура 7). Графически представленные законы изменения момента и равнодействующих всех левых сил по длине балки называют эпюрами моментов и поперечных сил (смотрите Балки простые).

Из рассмотрения фигура 7 можно вывести зависимость: tga₂= ^ и вообще tg Так как а_п есть угол, образуемый лучом п + 1 относительно 1-го луча, то вообще

. dlfyi ili V)

tg ^an=но а потому

_tr dy_n d (М_п 1 dMn ^{LS n} dx dx H ) H dx ’

откуда Q_n (теорема Шведлера). T. о. производная от момента внешних сил для какой-либо точки балки равна поперечной силе для этой балки.

Если вместо сосредоточенных грузов будет иметь место непрерывно распределенная сплошная нагрузка (фигура 11), то ее можно рассматривать как систему бесконечно большого числа бесконечно малых грузов, расположенных бесконечно близко друг к

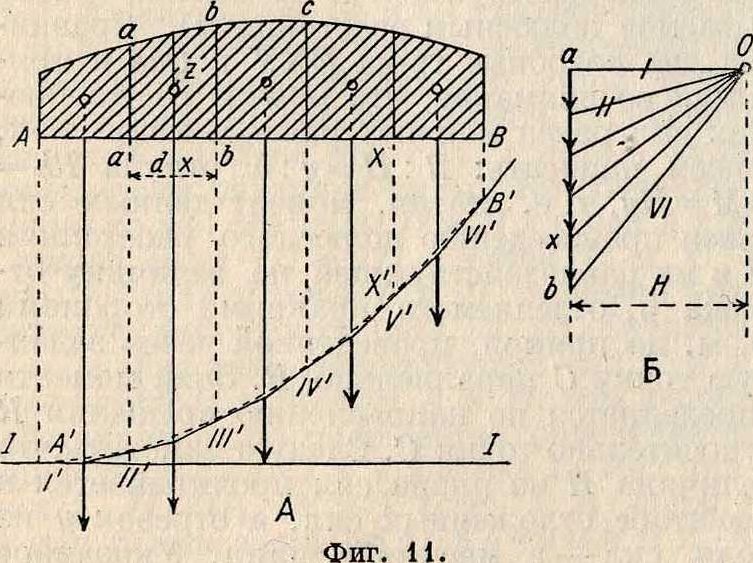
другу. Для такой системы сил В. м. обратится в плавную кривую, называемую в е-ревочной кривой. Заданную сплошную нагрузку переменной интенсивности z делят вертикальными прямыми аа, bb и т. д. на ряд участков, определяют нагрузку, соответствующую каждому участку, и эти нагрузки откладывают в определенном масштабе на мн-ке сил (фигура 11, Б). Система лучей, проведенных через произвольный полюс О к началу и концу каждого из отложенных отрезков I, II,., VI, определит направления сторон В. м. Г, IT,.,VI. Искомая веревочная кривая будет являться вписанной в построенный В. м. Точками касания явля ются точки пересечения сторон В. м. с вертикальными прямыми, разделяющими заданную сплошную нагрузку на ряд сосредоточенных сил. Это следует из того, что на границе участков ординаты В. м. и искомой веревочной кривой должен быть одинаковы, т. к. и та и другая ординаты определяют на границе участков момент всех сил, расположенных левее этой границы, а силы у них общие. При расположении полюса О с левой стороны, кривая, очевидно, будет являться описанной около веревочного многоугольника.

Так как направления касательных параллельны соответствующим лучам мн-ка сил, то отсюда можно вывести дифференциальное ур-ие веревочной кривой. Действительно, для касательной в точке х имеем:

X

y’=tga=~2*-da;

fz-dx Η *

а

Дифференцируя, имеем:

, 7 z-dx , z

у dx= _Η-, откуда У

Это и есть дифференциальное уравнение веревочной кривой.

Если закон изменения интенсивности нагрузки z нам известен, то путем интегрирования полученного выражения можно найти ур-ие соответствующей веревочной кривой. г-р

Фигура 13.

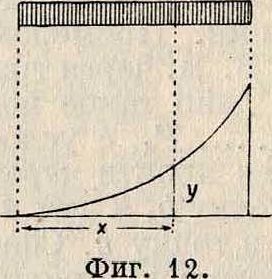
1- и случай. Сплошная нагрузка равномерно распределена вдоль горизонтальной оси. Величина е—р будет постоянной

(фигура 12). Т. о. «/"=—. Интегрируя, имеем:

У=С; у -у+ Сх + D.

Постоянные интегрирования м. б. определены, если задано по условию положение той прямой, от которой надлежит производить отсчеты ординат. Так, например, если направление I луча должно являться такой прямой, то имеем, что, при х=0, у=у= 0. Подставляя эти значения абсцисс и ординат в выражения у и у, получаем С=П= 0, и уравнение веревочной кривой примет вид:

у=то есть веревочная кривая представляет собою параболу.

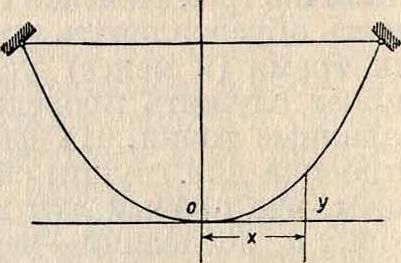
2- и случай. Сплошная нагрузка равномерно распределена по длине той кривой, какою должен быть сама веревочная кривая (собственный вес тяжелой гибкой нити). В этом случае веревочная кривая представляет собою цепную линию, то есть ту форму, которую принимает подвешенная в двух точках гибкая тяжелая (но нерастяжимая нить) под влиянием собственного веса q₀ кг/м (фигура 13). В данном случае

_Гд_е ~ — производная от ур-ия искомой веревочной кривой. Т. о. дифференциальное уравнение цепной линии:

у"⁼⁹нУ" ¹ + (»^/)² ·

Интегрируя выражение дважды и выбирая начало координат, как указано на фигуре 13, имеем:

“ 2д„

Величина полюснбго расстояния Н определится из условия, что длина цепной линии s

S=S ds равна заданной длине троса, о

Одно из самых важных приложений ур-ия веревочной кривой в строительной механике основано на совпадении этого ур-ия с ур-ием упругой линии—изогнутой оси балки (смотрите Упругая кривая).

Лит.: В е л и х о в П. А., Теория инш. сооружений, вып. 1, М., 1924; Тимошенко С. П., Курс

Веретенные масла Нефтеси