> Техника, страница 29 > Взаимность перемещений

Взаимность перемещений

Взаимность перемещений. Это положение было доказано Бетти (Е. Betti) в 1872 г. Оно имеет вид:

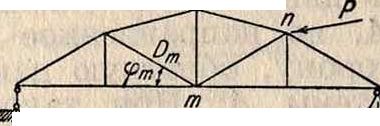
и формулируется так: «если какая-либо система находится последовательно под действием нагрузок S„ (1-е состояние) и нагрузок S_m (2-е состояние) или наоборот, то возможная работа сил первого состояния (S_n) на перемещениях 6_пт, вызываемых силами второго состояния (&_т) по направлениям первых, равна возможной работе сил второго состояния (S_m) на перемещениях 6_тп, вызываемых силами первого состояния (8„) по направлениям сил второго состояния». Напр., если на ферму (фигура 1) действует сила Р_п, вызывающая изменение наклона раскоса D_m к горизонту на величину А<р_тп (1-е состояние), и затем подействует пара сил с моментом М_т, вызывающая перемещение узла п на

1-е состояние

	2-е состояние
: ёв SL
	сР.Ч
L Δ

величину f_nm (2-е состояние), то, по смыслу теоремы Бетти, можно написать:

P«/jim⁼ МтА ⁽Ртп

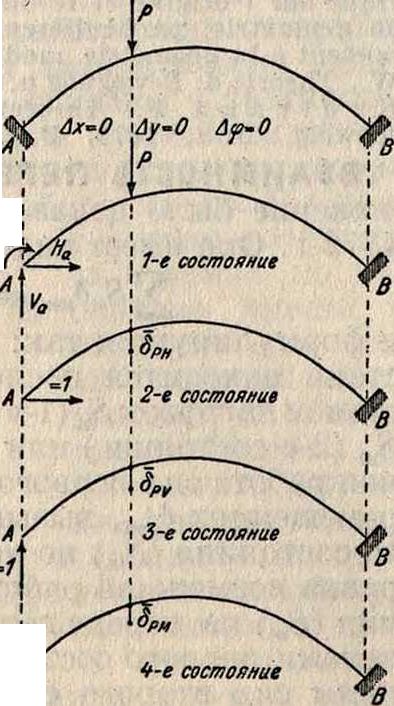
Это положение имеет большое применение в расчетах статически неопределимых систем; оно облегчает написание уравнений, недостающих для расчета этих сис тем. Наприм.,если рассматривать арку, заделанную пятами (фигура 2), представляющую собой трижды статически неопределимую систему, то, приведя эту арку к виду ста-ф_ИГ. i. тически определи мого кривого бруса с приложенными к нему неизвестными Н_а, V_a и М_а, можно рассматривать этот брус в следующих четырех состояниях загр ужения:

1- е, действительное состояние: нагрузки: Р, Н_а, V_a, М_а

деформации: Ах—О, Ау=0, А<р=0;

2- е, воображаемое состояние:

перемещения: брн, бнн, бун, бмн нагрузка: 1 — — ;

3- е, воображаемое состояние:

перемещения: dpv, 6hv, 6w, 6mv;

нагрузка: — 1 — ;

4- е, воображаемое состояние:

перемещения: брм,бнм,бум,бмм нагрузка:

Это дает возможность составить следующие уравнения:

РбрнА-Н_абнн + V_a6vH +М_а0мн=1-4х=0;

Ρδρν +H_a0HV + V_a6vv +M_a0MV =1-Ay=0;

Рбр м+Н_пбн μ + VJv м+М_абм μ=1· Αφ=0.

Далее остается упрощение этих уравнений, вычисление величины δ в них и решение их относительно неизвестных Н_а, V_a и М_а. Частный случай теоремы о В. п. был доказан еще в 1864 г. Максвелом (С. Maxwell), к-рый „ показал, что б_пт =

=б_тп. Это положение формулируется так: «если на систему действуют две количественно равные нагрузки, то перемещение (б„_т), вызываемое действием второй нагрузки (т) по направлению первой (и), количественно ί; равно перемещению, вызываемому действием первой нагрузки (и) по направлению второй (т)». Напр., если на балку действует сила Р_п=С кг и момент М_т=С кгм

— — 1.

Фигура 2.

(фигура 3), то прогиб f_nm, вызываемый моментом М_т по направлению силы Р_п,. будет равен углу поворота <р_тп, вызываемому действием силы Р„ по направлению момента М_т, т. e. f_nm=<p_mn.

Эта зависимость позволяет заменять сложное по вычислению перемещение б_тп более простым по вычислению перемещением S_nm. Кроме того эта зависимость позволила перейти от эпюр перемещений и линий прогибов к линиям влияния в статически неопределимых системах. Напр., если бы для двухшарнирной арки, представляющей собой однажды статически неопределимую систему, требова-

мт=с (S	Р*С
1 1 1	п [ 1 1 1 1

~Г

Фигура 3.

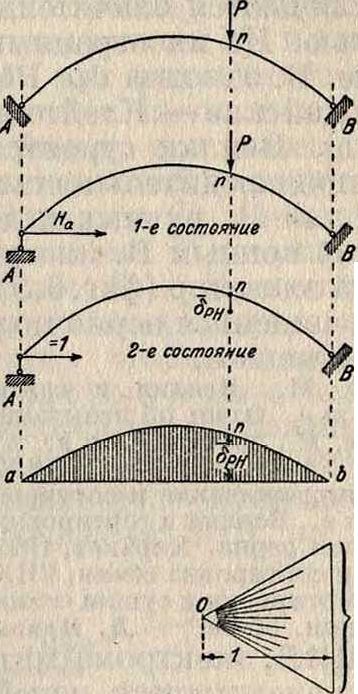
лось построить линию влияния распора Н, то это построение может быть сделано на основании следующих соображений. Приведя арку к виду статически определимого кривого бруса, лежащего на двух опорах (фигура 4), строим для него эпюру перемещений, как веревочную кривую апЬ для упругих грузов w. Каждая ордината этой кривой определяет собой величину вертикального перемещения брн любой точки п оси арки. Так как, по теореме о взаимности перемещений, брн —бнр, то, следовательно, ординаты той же кривой определяют собой величины перемещения точки приложения силы Ή от ^г” действия силы Р=1, приложенной в точке п оси арки, и так как эти ординаты изменяются в зависимости от положения груза Р=1, то, следовательно, кривая апb представляет собою линию влияния перемещения точки А по направлению силы Н_а-Рассмотрим зависимость между нагрузками Р=1 и Н_а в условиях 1-го и 2-го состояний:

1- е, действительное состояние:

Р=1, Н_а Ах=0

2- е воображаемое состояние:

бра, бнн! 1,

— _ 1брн откуда Рбрн+Нбнн=0 или Н_а=-=—.

бнн

Из этого следует, что кривая апb с ординатами брн может быть рассматриваема как линия влияния неизвестной силы Н_а при условии измерения этих ординат в масштабе

⁶нн- См. Линии влияния.

Лит.: П р о к о ф ь е в И. П., Теория сооружений, ч. II, М., 1928; Тимошенко С. П., Куре сопротивления материалов. Работа внутренних сил упругости, 5 изд., М.—П., 1923; Филоненк о-Б о р о-дич Μ. М., Основы теории работы упругих сил в

Фигура 4.

плоских системах, М., 1925; Кирпичев В. Л., Лишние неизвестные в строительной механике, Киев, 1903; Р i г 1 et J., Kompendium der Statik der Bau-konstruktionen, Berlin, 1921—23; Maxwell C., On the Calculation of the Equilibrium a. Stiffness of Frames, «Philosophical Magazine», London, 1913, v. 27, p. 294; Betti E., «Nuovo Cimento», Pisa, 1872, (seria 2), t. 7—8. Й. Прокофьев.