> Техника, страница 29 > Виллиса теорема

Виллиса теорема

Виллиса теорема устанавливает основное требование, которому должны удовлетворять профили зубцов зубчатых колес при правильной передаче, удовлетворяющей условиям непрерывности зацепления и постоянства передаточного числа зубцов. Пусть А и Б—зубцы двух колес, соприкасающиеся в точке В, причем О_г и 0₂—оси вращения колес. Скорость точки В, принадлежащей зубцу А, равна ν₁=ω_ιΕ₁, скорость той же самой точки В, но принадлежащей зубцу В, равна г>₂=й>₂Д₂, где ч>₁ и со₂—угловые скорости, a и Й₂—радиусы-

векторы. Разложим v_x и на их составляющие по направлениям: NN—общей нормали к профилям в точке В и ТТ—общей касательной. Из чертежа видно, что -Д =

= -гт, откуда с,=ν₁-^·=ма. Равным обра-

Κι Κχ

зом с₂=»₂ ~=ω·ί>₂, где ?! и ?₂ — длины перпендикуляров, опущенных из центров 0₁и О а на линию NN. При правильной передаче с₁=е₂, т. к. зубцы не могут внедриться друг в друга и отстать один от другого; еле-

О), 0.

довательно,=ω₂ρ₂, откуда —=— ·

U>₂ pj

Для равномерности хода это отношение должен быть постоянным. Из чертежа видно, что

— — °^гР — — — i — Const н ^_о,р~ _Γι-ί —oonst,

где i—передаточн. число, 0₂Р =г₂ и О_хР=г_х— радиусы начальных окружностей пары зубчатых колес; но О_х0₂=г_х+г₂ есть величина постоянная, поэтому точка Р—пересечение нормали к профилям с линией центров— получает неизменное положение на линии центров. Т. о., по В. т., профили зубцов должен быть

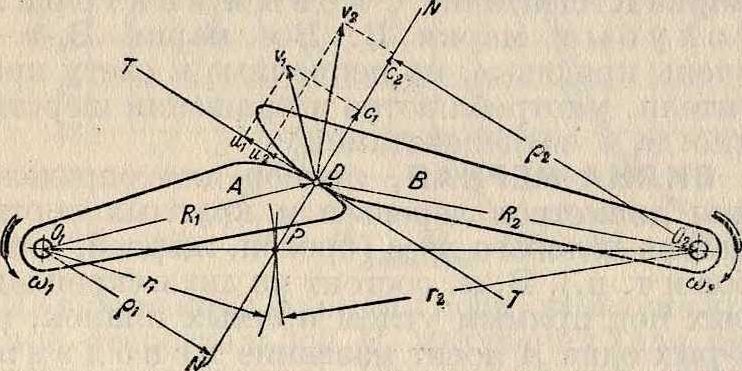
подобраны так, чтобы в любой момент движения общая нормаль к ним в точке касания проходила через одну и ту же точку Р, которая называется полюсом зацепления и является заданной точкой касания начальных окружностей для данной пары зубчатых колес.