Винт

Винт (в т е о р е т и ч е с к о и механи-к е). Для каждой системы приложенных векторов имеется нек-рая прямая, называемая главной осью системы, которая обладает тем свойством, что для любой ее точки (полюса) главный вектор и главный момент системы направлены по этой же прямой, причем совершенно безразлично, какую механическую величину система представляет, двух векторов, лежащих на одной оси, эквивалентная целой системе приложенных векторов, называется винтом, причем главный вектор А называется амплитудою винта, а частное от деления длины

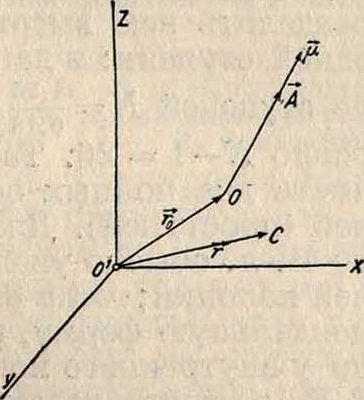
Такая совокупность вектора главного момента μ на длину вектора А называется параметром р винта,

р=и μ= р-А. Винт вполне определяется шестью величинами, а именно: четырьмя величинами, определяющими положение главной оси в пространстве, параметром и амплитудою. Можно определить В. также посредством радиуса-вектора г₀, определяющего положение полюса О на оси по отношению к некоторой системе отсчета, вектора-амплитуды А и параметра р, что равносильно наличию семи величин, вследствие чего одной из составляющих вектора г₀ может быть придано произвольное значение. Момент Ж винта относительно какой-либо точки С, положение которой определяется радиусом-вектором г, равняется

М=рА + _(г„ — г)А]. (1)

В качестве системы приложенных векторов можно взять систему сил, приложенных к твердому телу, причем, как известно, ее можно привести к такой равнодействующей силе .В и к такой равнодействующей паре, чтобы направление момента Ж последней совпало с направлением Л. Т. о. совокупность jB и Ж,эквивалентная данной системе,

представляет собой В. с параметром р= и амплитудою -В или динаму системы сил. Точно так же скорость движения точки твердого тела состоит из соответствующих данному моменту_мгновенной угловой скорости вращения со около некоторой оси (мгновенная ось вращения) и поступательной скорости и вдоль этой же оси, так что совокупность ω и и представляет собой также

В. с параметром р=— и амплитудою о>, или

винтовую скорость движения точки. Т. о. видно, что между Л и «), с одной стороны, и Ж та и, с другой, существует полная аналогия. Эти свойства аналогичности между кинематическ. и динамич. векторами были положены в основу выработки общих правил действий над ними, независимо от их механического значения, чем достигается большая общность в выводах различных между собой отделов механики. Так, например, пользуясь ф-лой (1) имеем: 1) момент дина-мы системы сил Мд. относительно точки С: Жа.=Ж + [(г₀ — г)Л] =рЛ + [(г₀ — г)Л] и 2) момент Же. винтовой скорости движения точки относительно С^_

Ж_в.=и + [(г₀ — г)о]=ρω + [(r_e — г) ω].

См. также Моторное исчисление.

Лит.: Жуковский Η. Е., Теоретик, механика, ч. II, М., 1927; Занчевский И., Теория винтов и приложения ее к механике, Одесса, 1889; Ball R. S., Theory of Screws, London, 1876; Ball R. S., Theoretische Mechanik starrer Systeme, Berlin, 1889; Schell W., Theorie der Bewegung und der Krifte, 2 Aufl., Lpz., 1880; T 1 m e г d i n g Η. E., Die Theorie d. Kraftepline, Lpz., 1910; Mises R., «Ztschr. fur angewandte Mathematik und Mechanik», Berlin, 1924, 4. M. Серебренников.