Вихревые токи

Вихревые токи, токи Фуко, токи, возникающие в проводниках, расположенных в вихревом электрическ. поле. По закону индукции (смотрите) скорость уменьшения магнитного потока через данную поверхность (магнитный спад) равна электрическ. напряжению вдоль контура, ограничивающего эту поверхность (циркуляции вектора напряженности электрическ. поля).Т. о. изменение магнитного потока создает вихревое электрич. поле, не имеющее потенциала и характеризуемое замкнутыми силовыми линиями или, во всяком случае, линиями, не имеющими ни начала ни конца. Поскольку в этом вихревом поле расположены проводники электричества, в них возникает (индуктируется) ток, плотность которого j, по закону Ома, пропорциональна вектору напряженности электрического поля: j=).E, где Я—удельная проводимость. С этой точки зрения токи, индуктируемые в обмотках трансформаторов и электрич. машин, т о-же являются В. т.; однако, благодаря сравнительно малому сечению применяемых проводов и специальному их расположению, индуктируемые в этих проводах токи легко вычисляются и м. б. направлены желательным для эксплуатации образом. Поэтому принято называть В. т. только такие индуктированные токи, которые замыкаются в вихревом электрич. поле. Токи, индуктируемые в обмотках электрич. машин и трансформаторов, выводятся наружу, за пределы вихревого электрич. поля. Это позволяет сравнительно просто рассчитывать электрическ. цепь таких токов, вводя понятие эдс, индуктируемой в той части цепи, которая расположена в вихревом поле. Вместо действительного вихревого поля рассматривается эквивалентное ему потенциальное поле, в котором распределены эдс с таким расчетом, чтобы их сумма во всей цепи как-раз равнялась скорости уменьшения магнитного потока. Тогда сумму эдс в этой цепи можно считать равной омическому падению напряжения во всей цепи (смотрите Индукции закон). Такой упрощенный расчет невозможен при определении вихревых токов в массивных проводах. Здесь введение эдс вместо рассмотрения вихревого поля только осложнило бы расчет. Поэтому для определения В. т. приходится интегрировать дифференциальные уравнения Максвела в данной среде, с учетом граничных условий задачи. Там, где этот расчет оказывается слишком сложным, пользуются эмпирическими формулами и определяют соответствующие коэффициенты опытным путем.

Возникновение В. т. во многих случаях нежелательно, потому что они нагревают, по закону Джоуля, проводники. Кроме того они искажают магнитные поля и, по закону Ленца, ослабляют в машинах полезный магнитный поток, создавая необхо димость увеличивать соответствующие ам-первитки возбуждения. Можно провести аналогию между В. т. и трением. С одной стороны, трением пользуются для целого ряда движений (без трения невозможна ходьба), с другой—трение создает добавочные потери энергии. Так и В. т. Ими пользуются для получения во вторичных обмотках машин и трансформаторов полезных токов, но вместе с тем В. т. возникают во всех металлическ. частях машин и создают добавочные потери. Изучение В. т. тесно связано с изучением вытеснения тока или скин-эффекта (смотрите) в проводниках, т. к. в массивных телах плотность тока распределяется неравномерно, благодаря тому, что энергия электромагнитных волн поглощается по мере проникновения в толщу тела.

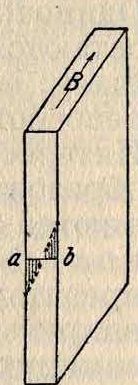
Потери в листовой стали. В железе трансформаторов и электрическ. машин пульсирует магнитный поток. Чтобы уменьшить потери от В. т., применяют пакеты, сложенные из тонких листов динамной стали, оклеенных для изоляции бумагой. Магнитные линии проходят параллельно поверхности листов, например в направлении вектора В (фигура 1). Тогда возникает вихревое электрич. поле в направлении, перпендикулярном В, причем плотность электрического тока возрастает при перемещении от середины листа к его поверхности. На фигуре 1 стрелками изображены значения по величине и по направлению плотности тока в различных точках линии аb (смотрите Индукции закон). Потери на теплоту Джоуля в 1 см³измеряются мощностью ρβ. Следовательно, для уменьшения этих потерь надо выбирать возможно более тонкие листы. На практике берут листы толщиной Λ в 1 миллиметров,

0,5 миллиметров и 0,35 миллиметров и выражают мощность V, поглощаемую вихревыми токами в 1 килограмм листовой стали, формулой:

где f—частота, Б—индукция и а—опытный множитель, зависящий от электрич. сопротивления материала, от толщины листов и от формы кривой, по которой изменяется индукция. Так, например, при толщине листа и=0,5 миллиметров, для обыкновенной динамной супали (смотрите) σ=5,6, а для стали с примесью кремния <7=1,2. При толщине //=0,35 миллиметров, а соответственно=3,2 и 0,6. При больших частотах или при толстых листах формула (1) нуждается в поправке, потому что вихревые токи деформируют поле, и тогда индукция распространяется по величине и по фазе неравномерно в толще листа. Вводим приведенную толщину листа £=где а— 2яр (ί> в Ω миллиметров²/м).

Так, например, при μ=3 000, (>=0,15амм“/м, /1=0,5 миллиметров, /= 50 си"¹ имеем £=0,99. Отношение индукции В в любой точке на расстоянии ж сантиметров от средней плоскости листа к индукции B_s на поверхности определяется по следующей формуле:

-Δ—

Фигура 1.

ch <χχ 4- cos 2<χχ

_е - (2)

ciu + COSi ^ν

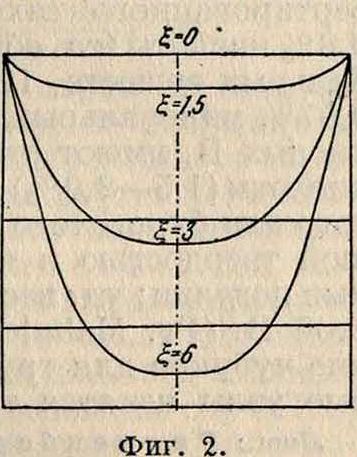
На фигуре 2 изображены значения в зависимости от х при различных значениях §. Горизонтальные линии изображают соот-

Вт ветствующие значения отношения где

В_т—среднее значение индукции по толщине листа. При той же самой средней индукции потери от В. т. увеличиваются при больших частотах в отношении

, 3 shq — sini ,._ON

^Кт - Т chi—"cosi · W

Уже при ξ > 3 можно считать k_m ^ -ξ-, так что потери в единице объёма выразятся формулой:

7=А-2

где или

ВЦ, W/сж³,

1,256-10 (лН/сл1,

(4)

(4а)

При тех же частотах удобнее относить потери не к единице объёма, а к единице поверхности. Тогда, если распределить потери на обе поверхности листа,

F„=iz/-F

V₀ не зависит от толщины листа, потому что почти все В. т. вытеснены на поверхность листа. В этом случае формула (5) применима и к массивному железному цилиндру, в котором пульсирует магнитный поток в осевом направлении.

Приведенные формулы нуждаются еще в поправке, потому что на самом деле проницаемость μ зависит от индукции, но эту поправку весьма трудно вычислить. Обыкновенно берут некоторое среднее значение для μ. Вторую поправку следует ввести, если колебания индукции происходят не по закону синуса. Тогда кривую колебаний разлагают на отдельные гармонические колебания и вычисляют потери для каждой гармоники в отдельности.

В якоре электрич. машин нельзя считать магнитное поле однородным. При расчете В. т. следует принимать во внимание искривление линий индукции и линий тока.

В этом случае потери в якоре от В.т. определяются по формуле:

Qw=К F · М. Здесь М—масса железа якоря, F—потери, определяемые по формуле (1), где f—частота пере-магничивания и В— средняя индукция в якоре. Наконец, поправочный множитель Tt_wзависит от числа полюсов р и от отношения

-^—радиальной толщины потока к полюс

ному делению. На фигуре 3 указаны значения k_w (вычисленные Рихтером).

Аналогично вычисляются потери от В. т. в зубцах якоря, в полюсных башмаках ит. п. В проводах, расположенных в пазах электрич. машин, тоже появляются В. т., связанные с вытеснением тока на поверхность проводников. Это обстоятельство также создает увеличение потерь в проводах.

В.т. при коммутации. При перемене режима вихревые токи тоже играют большую роль. Рассмотрим, наприм., простой случай выключения или включения электромагнита с массив, сердечником. Решение таких задач рассматривается в электродинамике (См.). Можно, однако, физически представить себе, что каждое изменение магнитного потока создает В. т., охватывающие этот поток. Явление выключения электромагнита можно рассматривать следующим образом. Магнитное поле в сердечнике, к-рое до выключения было постоянным в пространстве и во времени, распадается на ряд отдельных полей, распределенных волнообразно в пространстве, причем каждое поле исчезает со своим коэффициентом затухания. Мы предполагаем, что электромагнит состоит из двух стержней, ярма и притягиваемого якоря. Тогда, если 4 будет приведенная полная длина воздушного зазора и /I будет активная длина магнитных линий в железе, то, применяя дифференциальные уравнения Максвела и пренебрегая токами смещения, мы получим для магнитной индукции дифференциальное уравнение:



					7
					t
<л	утре ЯК Ор	Hf/UU.		Λ		-
			*	к.	’ 4.
					—£	корь

oj 0,2 о,з £ о“ as Фигура 3.

гв=y-i-w- ^

Возьмем для упрощения магнитный стержень прямоугольного сечения. Тогда уравнение (6) принимает вид:

дВ, д’В 4 π Δ дБ

дх^{г т} ду^г р δ at

(6а)

и может быть проинтегрировано так:

Β=ΣΐΒ _m,„-COs(i

n т ⁴

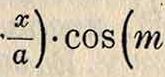
vj._e-<p_B,m,₍₇)

где множитель затухания

-.-i·4 [(=?) +(7)’]·

здесь п и т могут иметь любые целые значения, а В_п<т зависит от граничных условий; так, например, если до выключения поле В₀ было постоянным в пространстве и во времени, то

В„,т=± (у)², И в частности В,, =(у)²В₀-

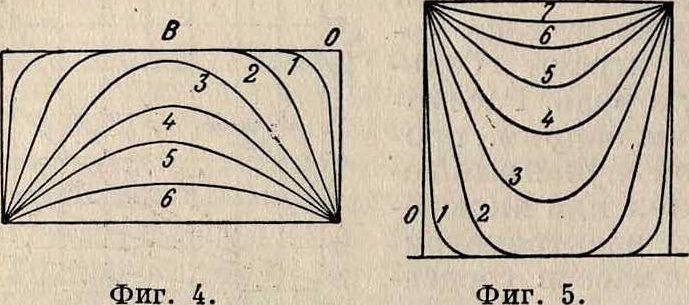
Высшие гармоники В,_|)ОТ очень быстро уменьшаются с возрастанием порядкового номера, и мы должны учитывать главным образом основную волну; ее амплитуда на 62% больше первоначального постоянного поля В₀. Фигура 4 показывает распределение индукции в магнитном стержне для различных моментов времени. Мы видим, что в середине магнита поле остается дольше всего. При включении, наоборот, поле только постепенно проникает внутрь магнита, как видно из фигура 5, дающей распределение индукции в магнитном стержне для различных моментов времени.

Полезные применения. В. т. применяются для торможения, когда, например,

электромагнит помещают против скользящей или вращающейсяферромагнитной детали. Т. о. выполняют электромагнитное успокоение измерительных приборов, электромагнитное торможение двигателей. В. т. применяются также в металлургических печах большой частоты, для нагревания руды. Наконец, В. т. применяются и в двигателях, например в предложенном К. И. Шейфером асинхронном двигателе, якорь которого состоит из массивного железного цилиндра.

Лит.: Круг К. А., Основы электротехники, Москва, 1926; Rich te R., Elektrische Maschinen, В. 1, В., 1924 (в лит. указателе перечислен ряд монографий по В. т.); Riidenberg R., Elektr. Schalt-vorgange usw., 2 Aufl., B., 1926. Я. Шпильрейн.