> Техника, страница 31 > Водяной пар

Водяной пар

Водяной пар. Паром называется газообразное тело, получающееся из жидкости при соответствующих t° и давлении. Все газы м. б. обращены в жидкое состояние, и поэтому трудно провести границу между газами и парами. В технике паром считают газообразное тело, состояние которого недалеко от обращения в жидкость. Т. к. в свойствах газов и паров имеются значительные различия, то это различие терминов вполне целесообразно. Водяные пары являются важнейшими из паров, применяемых в технике. Они употребляются, как рабочее тело, в паровых двигателях (паровых машинах и паровых турбинах) и для целей нагревания и отопления. Свойства пара чрезвычайно различны, смотря по тому, находится ли пар в смеси с той жидкостью, из которой получается, или он отделен от нее. В первом случае пар называется насыщен-н ы м, во втором случае—п ерегретым. В технике первоначально применялся почти исключительно насыщенный пар, в настоящее время в паровых двигателях находит самое широкое применение перегретый пар, свойства которого поэтому тщательно изучаются С¹].

Ϊ. Насыщенный пар. Процесс испарения лучше уясняется графич. изображениями, иапр. диаграммой в координатах р, v (удельное давление в килограммах/см² и удельный объём в м³/кг). На фигуре 1 изображен схематически процесс испарения для 1 килограмм воды. Точка а₂ изображает состояние 1 килограмм воды при 0° и давлении р₂, причем абсцисса этой точки изображает объём этого количества, ордината—давление, под которым находится вода. Кривая а_гаа₁ показывает изменение объёма 1 килограмм воды при повышении давления. Давления в точках а₂, а, а_г соответственно равны р₂, р, р_г кг/см³. Фактически это изменение чрезвычайно мало, и в технич. вопросах можно считать удельный объём воды не зависящим от давления (то есть линию а₂аа₁ можно принимать за прямую, параллельную оси ординат). Если нагре-

вать взятое количество воды, сохраняя давление постоянным, то t° воды повышается, и при некоторой величине ее начинается испарение воды. При нагревании воды уд. объём ее, теоретически говоря, несколько увеличивается (по крайней мере, начиная с 4°,

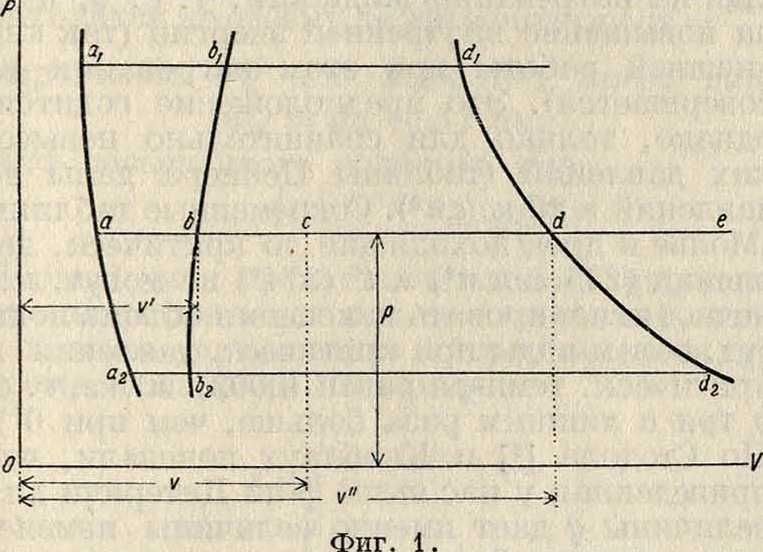
то есть от t° наибольшей плотности воды). Поэтому точки начала испарения при разных давлениях (р₂, р, р_х) будут лежать на некоторой другой кривой δ₂δδ₂. Фактически это увеличение объёма воды при повышении t° незначительно, и потому при невысоких давлениях и t° можно принимать уд. объём воды за постоянную величину. Уд. объёмы воды в точках δ₂, b, b_х обозначаются соответственно через ν₂, ν, ν_χ, кривая bфb_х называется нижней предельной кривой. Температура, при которой начинается испарение, определяется тем давлением, под которым находится нагреваемая вода. За все время испарения эта t° не изменяется, если давление остается постоянным. Отсюда следует, что ί° насыщенного пара есть функция только давления р. Рассматривая какую-либо линию, изображающую процесс испарения, например bed, видим, что объём смеси пара и жидкости в процессе испарения возрастает по мере увеличения количества испарившейся воды. В некоторой точке d вся вода исчезает, и получается чистый пар; точки d для разных давлений образуют некоторую кривую d_xdd₂, которая называется верхней предельной кривой, или кривой сухого насыщенного пара; пар в этом состоянии (когда только что закончилось испарение воды) называется сухим насыщенным паром. Если продолжать нагревание после точки d (по направлению к некоторой точке е), оставляя давление постоянным, то t° пара начинает повышаться. В этом состоянии пар называется перегретым. Таким образом получаются три области: правее линии d_xdd₂—область перегретого пара, между линиями b₁bЬ₂ и d_xdd₂—область насыщенного пара и левее линии b_хЬЬ_г—область воды в жидком состоянии. В какой-либо промежуточной точке с имеется смесь пара и воды. Для характеристики состояния этой смеси служит количество х содержащегося в ней пара; при весе смеси в 1 килограмм (равном весу взятой воды) эта величина х называется пропорцией пара в смеси, или паросодержанием смеси; количество воды в смеси будет равно (1— х) кг.

Если v" м³/кг—уд. объём сухого насыщенного пара при темп-ре t и давлении р кг/см², а объём воды при тех же условиях ν, то объём смеси υ найдется по формуле: v=χν"+ (1 — x)v,

или

v=χ(ν" — ν) + ν.

Объемы ν и ν, а следовательно, и их разность v— v суть функции давления р (или температуры t).

Вид функции, определяющей зависимость р от t для водяного пара, очень сложен; существует много эмпирическ. выражений для этой зависимости, которые все, однако, годятся лишь для нек-рых ограниченных интервалов независимой переменной t. Реньо для t° от 20 до 230° дает ф-лу:

lg р=a — bet +²⁰ — ββ^ι +²⁰,

где a=6,2G40348, lg et=0,998343862 -1, lg β=0,994049292 -1, lg δ=0,6924351, lg с=0,1397743.

В настоящее время часто пользуются формулой Дюпре-Герца (Dupr6-Hertz) [*]:

Igp=k — mlg T — ^, где k, m и n—постоянные.

Шюле [³] дает эту формулу в след, виде: lgp·=А — ~,

¹ S

при чем для t°:

а) между 20 и 100°

lgp=5,9778 -?^

(р—в кг/см², Т—абсолютная темп-pa пара);

б) между 100 и 200°

Ί г пл ост 2101,1

lgp=5,6485 --„ ;

в) между 200 и 350°

lgp=5,45142-

2010,6

Характер кривой давления р пара как функции температуры виден на фигуре 2.

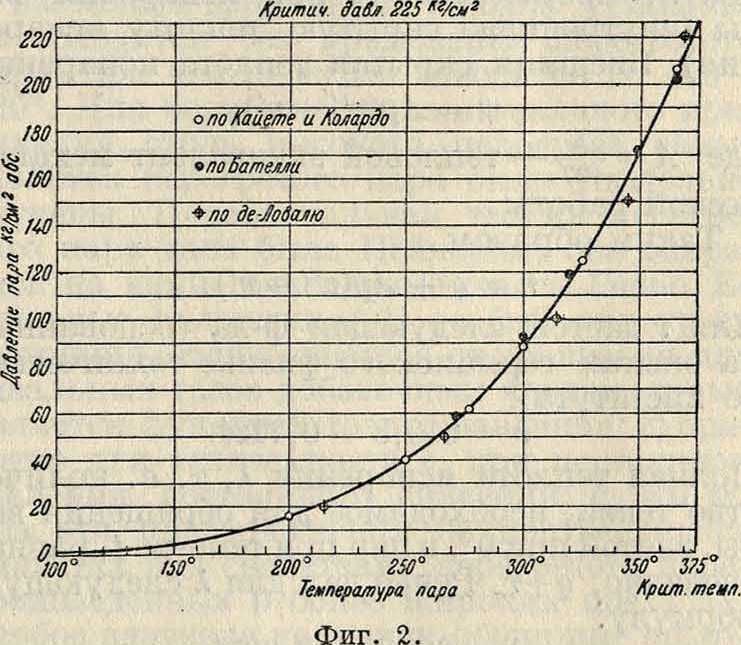
В практике пользуются непосредственно таблицами, дающими связь между р и t. Таблицы эти составляются на основании точных опытов [⁴, ⁵, ⁶]. Для нахождения удельных объёмов сухого насыщенного пара имеется теоретически выводимая формула Клапейрон-Клаузиуса.Можно пользоваться также эмпирической формулой Молье [’]:

1>"Р"= 1,7325.

Количество тепла q, необходимое для нагревания 1 килограмм воды от 0 до <° (начала испарения), выражается так:

t

q =§cdt, о где с—теплоемкость воды, в широких пределах мало отличающаяся от единицы; поэтому пользуются приближенной формулой:

2=*·

Однако уже Реньо убедился в заметном возрастании с при высоких темп-pax и дал для q выражение:

q=* + 0,00002*² + 0,0000003*³.

В новейшее время для с даются такие данные (ф-ла Дитеричи):

с=0,9983 - 0,0001037* + 0,000002073<². Для средней теплоемкости с_т в интервале от 0 до *° дано выражение: с_т=0,9983 - 0,00005184* + 0.0000006912*².

Несколько отклоняются от этой ф-лы данные опытов германского физико-технич. института [*], наблюдения которого дают следующие значения с:

t°	1 0°	5°	10”	15”	20°
с	1 1.0050 1	1.0030	1,0013	1,0000	0,9990
Г	1 25“	30"	35"	40"	50"
с	1 0,9983	0,9979	0,9979	0,9981	0,9996 1

Для обращения в пар воды, нагретой до темп-ры “, нужно еще затратить нек-рое количество тепла г, к-рое называется скрытой теплотой испарения. В настоящее время эту затрату теплоты разделяют на 2 части: 1) теплоту ψ, идущую на внешнюю работу увеличения объёма при переходе воды в пар (внешнюю скрытую теплоту испарения), и 2) теплоту ρ, идущую на внутреннюю работу разъединения молекул, происходящую при испарении воды (внутреннюю скрытую теплоту испарения). Внешняя скрытая теплота испарения ψ=Apiv"— ν),

где А=-~ — тепловой эквивалент механической работы.

Таким образом г=ρ + Ap(v"— ν).

Для г дается следующая формула (основанная на опытах германского физико-технического института):

г=610,3-0,712*.

Полная теплота испарения λ, то есть количество тепла, необходимое для обращения воды, взятой при 0°, в пар при темп-ре “, равна, очевидно, q+r. Реньо дал для λ следующую формулу:

λ=606,5 + 0,305*;

эта формула дает результаты, близкие к новейшим опытным данным. Шюле [³] дает:

λ=608 + 0,311*.

Внутренняя энергия и воды при 0° принимается равной нулю. Для нахождения приращения ее при нагревании воды нужно выяснить характер изменения удельи. объёма воды при изменении давления и *°, то есть вид кривых ама₁ и b₂Ьb₁ (фигура 1). Про стейшим предположением будет принятие этих линий за прямые, и притом совпадающие друг с другом, то есть принятие уд. объёма воды υ за постоянную величину, не зависящую ни от давления, ни от <°(υ =0,001 м³/кг). При этом предположении вся теплота, идущая на нагревание жидкости, т. e. q, идет на повышение внутренней энергии (так как внешней работы при этом нагревании не совершается). Это предположение годится, однако, только для сравнительно невысоких давлений (таблицы Цейнера даны до давлений в 20 к г/см³). Современные таблицы (Молье и др.), доходящие до критическ. давления (225 килограмм/см²) и *° (374°) не могут, конечно, игнорировать изменения объёма воды (уд. объём воды при критическ. давлении и критическ. темп-ре равен 0,0031 м³/кг, то есть в три с лишним раза больше, чем при 0°). Но Сто дола [⁸] и Киоблаух показали, что приведенная у нас выше формула Дитеричи для величины q дает именно величины изменения внутренней энергии (а не величины q);

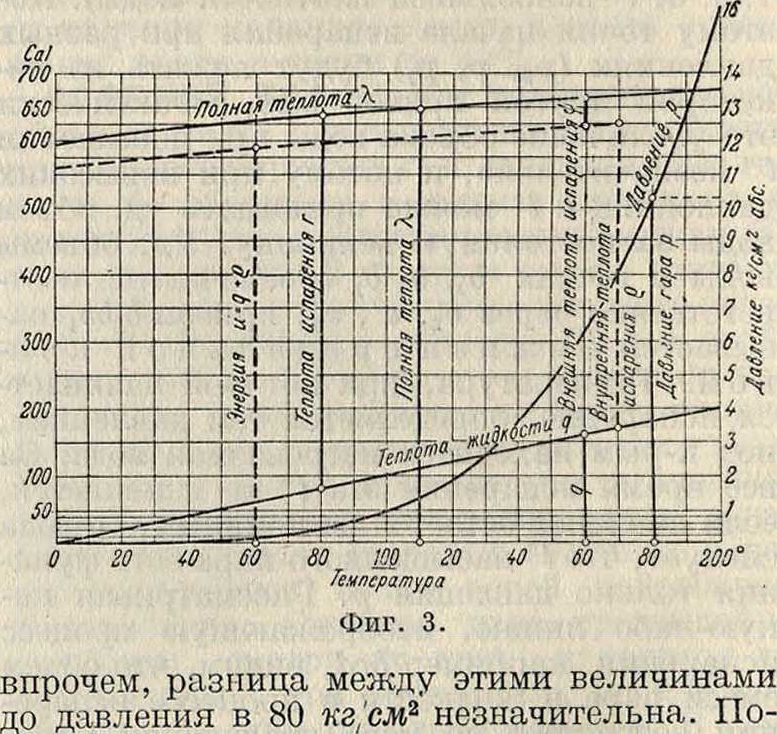
этому полагаем для воды внутреннюю энергию равной теплоте жидкости: u=q. За период испарения внутренняя энергия повышается на величину внутренней скрытой теплоты испарения ρ, то есть энергия сухого насыщенного пара будет: и”=q + ρ (фигура 3). Для смеси с пропорцией пара х получим следующее выражение:

и=q(l — х) + (з + ρ)χ=q + независимость теплоты испарения и давления от *° графически дана на фигуре 3.

Молье ввел в технич. термодинамику тер-модинамич. функцию г, определяемую уравнением i=и + АРо и называемую теплосодержанием. Для смеси с пропорцией пара х это даст:

г=q + χρ + ΑΡ χ{ν"— ν) + ν], или, после приведения:

i=q + xr + APv; для воды (ж=0) получается: i — q + APv·,

для сухого насыщенного пара: i”=q + г + APv.

Величина произведения APv очень мала по сравнению даже с величиной q (и тем более по сравнению с величиною q- -r=X) поэтому можно принять

*=3", i" ^q + r.

В таблицах Молье даются поэтому не величины q и Я, а величины г и i" в функции р или t°. Энтропия насыщенного пара находится по своему дифференциалу ds=^d®;

выражение dQ для всех тел имеет вид: dQ — du + АР dv.

Для насыщенного водяного пара

ds =

dq -fAPdv

ψ

(?)

Первый член представляет собою приращение энтропии воды при ее нагревании, второй член—приращение энтропии смеси во время испарения. Полагая

i

Ч

dq 4- APdv

получим ds=ds + d, или, интегрируя:

S — S H—jr ·

Заметим, что при вычислении s изменением уд. объёма ν обыкновенно тоже пренебрегают и полагают. Для решения всех вопросов, касающихся насыщенных паров, пользуются таблицами. В прежнее время в технике находили применение таблицы Цейнера, в настоящее время они являются устарелыми; можно пользоваться таблицами Шюле, Кноблауха [⁵] или Молье С¹’⁹]. Во всех этих таблицах давления и t° доведены до критич. состояния. В таблицы включены следующие данные: t° и давление насыщенного пара, уд. объём воды и пара и уд. вес пара, энтропия жидкости и пара, теплосодержание воды и пара, полная скрытая теплота испарения, внутренняя энергия, внутренняя, и внешняя скрытая теплота. Для некоторых вопросов (касающихся, наприм., конденсаторов) составляются специальные таблицы с малыми интервалами давлений или температуры [¹⁰].

Из всех изменений пара особенный интерес представляет адиабатическое изменение; оно м. б. изучено по точкам. Пусть дана (фигура 4) начальная точка 1 адиабаты, определяемая давлением р_ъ и пропорцией пара Χχ, требуется определить состояние пара в точке 2, лежащей на адиабате, проходящей через точку 1 и определяемой давлением р₂. Для нахождения ж₂ выражают условие равенства энтр в точках 1 и 2:

*1 + ^х1^=¹ " ^Г

В этом ур-ии величины s

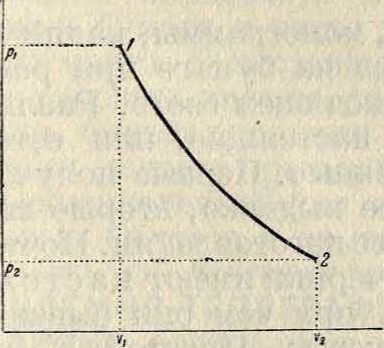
Фигура 4.

² То“

1’ _т

«2 И

на ходятся по данным давлениям р_г и р₂, пропорция пара х_г задана, и неизвестен толь ко ж₂. Удельный объём ν₂ в точке 2 определится по формуле:

ν₂=x₂(v₂ - τ) + ν.

Величины νί и ν₂ ^ находятся из таблиц. Внешняя работа рассматриваемого адиаба-тич. изменения находится по разности внутренних энергий в начале и конце изменения: AL=u₁-u₂=q₁ +×Qx — q₂ — ж₂р_а.

Для упрощения вычислений часто пользуются при изучении адиабатического изменения эмпирич. ур-ем Цейнера, который выражает адиабату как политропу: ρν^μ=р₀т£.

Показатель степени μ выражается через начальную пропорцию пара х_х так: μ=1,035 + 0,ί^χι·

Ф-ла эта применима в пределах от а?!=0,7 до Χχ=ί. Адиабатич. расширение при начальной высокой пропорции пара, выше 0,5, сопровождается обращением части пара в воду (уменьшением ж); при начальных пропорциях пара, меньших 0,5, адиабатич. расширение сопровождается, наоборот, испарением части воды. Формулы для остальных случаев изменения насыщенного пара находятся во всех учебниках технической термодинамики [“].

II. Перегретый пар. Внимание к перегретому пару привлечено было еще в 60-х годах прошлого столетия в результате опытов Гирна [^1!], показавших значительную выгоду при применении перегретого пара в паровых машинах. Но особенного распространения перегретый пар достиг после создания В. Шмитом особых конструкций перегревателей специально для получения пара высокого перегрева (300—350°). Эти перегреватели нашли широкое приложение сначала (1894—95 гг.) в стационарных паровых машинах, затем в паровозных машинах и в 20 веке—в паровых турбинах. В настоящее время почти ни одна установка не обходится без применения перегретого пара, причем перегрев доводится до 400— 420°. Для возможности рационального применения столь высокого перегрева самые свойства перегретого пара были тщательно изучены. Первоначальная теория перегретого пара дана была Цейнером; она опиралась на немногочисленные опыты Реньо. Ее основные положения: 1) особый вид ур-ия состояния, отличающегося от уравнения для идеальных газов добавочным членом, к-рый является функцией только давления; 2) принятие для теплоемкости с_р при постоянном давлении постоянного значения: ^=0,48. Оба эти предположения не подтвердились в опытах над свойствами перегретого пара, произведенных в более широких пределах. Особое значение получили обширные опыты Мюнхенской лаборатории технич. физики, начатые около 1900 г. и продолжающиеся и в настоящее время [¹³]. Новая теория перегретого пара была дана в 1900—1903 гг. Каллендером в Англии и Молье в Германии К¹), но и она не явилась окончательной, так как выражение для теплоемкости при постоянном давлении, получаемое из этой теории, не вполне согласуется с новейшими опытными данными. Поэтому появился целый ряд новых попыток построения ур-ия состояния для перегретого пара, которое бы более согласовалось с результатами опытов. Из этих попыток известность получило ур-ие Эйхельберга [¹⁴]. Окончательное завершение эти попытки нашли в новой теории Молье (1925—1927 гг.), поведшей к составлению его последних таблиц [⁸]. Молье принимает очень выдержанную систему обозначений, которой мы отчасти пользовались выше. Обозначения Молье: Р—давление в к г/м² абс., р—давление в килограммах/см² абс., v—удельн. объём в м³/кг, у=— УД. в килограммах/м³, ί—темп-pa от 0°,

Τ= ί° + 273°—абсолютная темп-ра, —

тепловой эквивалент механической работы, R= 47,1—газовая постоянная (для паров воды), s—энтропия, i—теплосодержание в Cal/мг, u — i—APv—внутренняя энергия в Cal/кг, φ=β — ~, с_р—теплоемкость при по стоянном давлении, с_р=0,47 —предельная величина с_р при р=0. Значки и " относятся соответственно к воде и к сухому насыщенному пару. Из ур-ия Молье

Pv

= 47,1 -0,02-

1,9 10* ’

(⁷|* Ш

Ю0 V100

при помощи ф-л, вытекающих из I и II закона термодинамики, получаются все важнейшие величины, характеризующие перегретый пар, т. e. s, г, и и с_р. Молье вводит следующие вспомогательные функции температуры:

суч 2 1,5613 г 202,96

$i=--;уi=--; Ji=-;

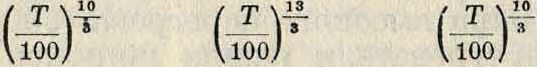
_m 1,9-10“, 2,0765· 10¹⁰ _t j _ 2,2248· 10“

7 ,:ι ’ I T 15 ’ -. Γ οι

uooj uooj uooj

При помощи этих функций получаются следующие выражения:

s =l,08221g Г-0,25399lg (ЮЭД-^р-у^)³;

»=0,47ί-Λρ-Γ₂(^)³ + 595; и=0,3597ί - 0,769 J,p - 0,8/₂(-^₅)³ + 564,9 ;

,=0,47 + 17^ + 15^^

Ί³·

Ф-лы для нахождения уд. объёма и прочих величин для перегретого пара довольно сложны и неудобны для вычислений. Поэтому новейшие таблицы Молье заключают в себе вычисленные значения важнейших величин, характеризующих перегретый пар в функции от давления и t°. К перегретым парам относятся табл.: III (дающая величины уд. объёмов перегретого пара), IV и У (заключающие в себе величины теплосодержаний и энтр для перегретого пара). В таблице VI содержатся величины вспомогательных функций, введенных Молье (в зависимости от t°). Наконец, в таблицах VII и VIII даны значения теплоемкостей перегретого пара по мюнхенским опытам (истинной и средней). При помощи таблиц Молье до вольно просто и с достаточной точностью решаются все задачи, касающиеся перегретого пара. Надо еще заметить, что для адиа-батич. изменения перегретого пара в известных пределах (до 20—25 килограмм/см²) сохраняет свое значение ур-ие политропич. вида: ргД.з—Const. Наконец, многие вопросы, касающиеся перегретого пара, м. б. решены при помощи графич. приемов, особенно при помощи диаграммы IS Молье. На этой диаграмме помещены кривые постоянных давлений, постоянных t° и постоянных объёмов. Т. о. можно прямо из диаграммы получать значения v, s, г в функции давления и t°. Адиабаты изображаются на этой диаграмме прямыми линиями, параллельными оси ординат. Особенно просто находятся разности величин теплосодержания, соответствующие началу и концу адиабатич. расширения; эти разности необходимы для нахождения скоростей истечения пара.

Лит.: *) Радциг А. А., Таблицы и диаграммы для водяного пара, 2 изд., М.—Л., 1928; *)×в о л ь-сон О. Д., Курс физики, 5 изд., т. 3, Берлин, 1923; ^!) S Chii 1 e W., Technische Thermodynamik, 4 Auli., В. 1, р. 204—205, В.·, 1923; *) Z e u η е г G., Technische Thermodynamik, 3 Aufl., В. 2, Lpz., 1906; *) Η о 1-born L., Scheel К. u. Henning F., Warmetabellen, Braunschweig, 1919; *) Knoblauch O., Baisch E. und Hausen H., Tabellen und Diagramme fur Wasserdampf, Miinchen, 1923; ’) Mollier R., Neue Tabellen u. Diagramme filr Wasserdampf, p. 10, B., 1906; “) StodolaA., Dampf-u. Gasturbinen, 5 Aufl., p. 1105, B., 1922; *) M о 1 I i e r R., Neue Tabellen und Diagramme fiir Wasserdampf, 3, 4 Aufl., B., 1925 — 27; ^lu) Hoefer K., Die Kondensation bei Dampfkraftmaschinen, Berlin, 1925; “) С у ш к о в В. В., Технич. термодинамика, М., 1926; ^1!) Him G. A., Mdmoire sur la thdorie de la surchauffe dans les machines ii vapeur, «Bull, de la Soc. Industrielle de Mulhouse», Mulhouse, 1857; *·) «Mitteilungen liber Forschungsarbeiten usw.», B., 1905—1917, H. 21, 35, 36, 108, 109, 195; «Z. d. VDI», B., 1922, p. 418; Ibid., 1927, 14; “) «Forschungsarbeiten usw », B., 1920, II. 220. А. Радциг.