> Техника, страница 32 > Воздушный

Воздушный

Воздушный винт, аппарат для получения силы тяги в воздухе за счет создания в этой среде нек-рого количества движения в ограниченной струе. Винт является почти единственным в настоящее время аппаратом, применяемым в области воздухоплавания и авиации.

Простейшим типом воздушного винта может служить т. и. геометрический винт, опорная поверхность которого представляет собою математичес.к. винтовую поверхность (смотрите). Из этой поверхности вырезают только часть, представляющую собою т. н. лопасть винта, укрепленную в ступице; ступица надевается на втулку, скрепленную с валом, вращающим В. в Для воспринятая получающихся на лопасти усилий их делают известной толщины и в сечен ш подобными крылообразным контурам. Чаще всего В. в имеет 2 лопасти, реже—3 и 4. Материалом для изготовления лопастей служат сталь, легкие сплавы и дерево. Наиболее распространенными являются деревянные В. в., но в последнее время получают распространение металлические винты, которые бывают двух типов: сплошные, из одного куска металла (дуралюминия), и и о-лые, из листового металла, с заваренными или склепанными швами и внутренними диафрагмами. В последнем случае лопасти приклепываются к ступице или привертываются при помощи муфты. Иногда сама ступица служит втулкой и надевается прямо на вал мотора.

Параметры, определяющие геометрич. размеры В. в., называются его геометрич. характеристиками. Главной геометрич. характеристикой винта является его диаметр D. В авиации величина диаметра винтов обычно заключается между 2 и 3 метров Другой геометрической характеристикой В. в является шаг. Шагом винтовой поверхности называется проекция (на ось) пути точки, двигающейся по этой поверхности на неизменном расстоянии от оси, за один оборот. Поверхность воздушного винта обычно отличается от винтовой поверхности тем, что сечения лопастей плоскостями, касательными к соосным винту цилиндрам, имеют форму, применяемую в крыльях аэроплана (смотрите Аэродинамика), которые иногда делаются вогнутыми; следовательно, можно

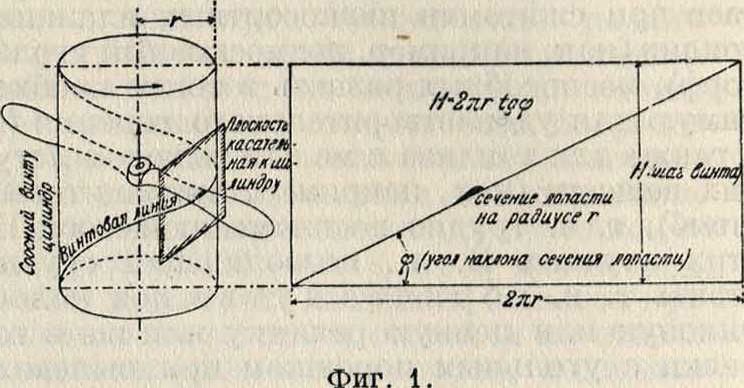
говорить лишь о том, что сечения лопастей будут касаться соответствующей винтовой линии. Таким образом в каждом сечении лопасти можно найти соответствующий этому сечению шаг винта, который будет через угол ψ наклона лопасти выражаться равенством (фигура 1): Н= Znrtg φ.

Если каждое сечение лопасти В. в касается одной и той же винтовой поверхности, то такие винты называются винтами с постоянным шагом, так как значение шага в каждом сечении лопасти остается постоянным; если в каждом сечении лопасти значение шага разное, то такие винты называются винтами с переменным ш а-гом. Закон изменения шага по лопасти зависит от конструкции винта; обычно от ступицы шаг винта увеличивается, достигает своего наибольшего значения * и к концу лопасти уменьшается (фигура

2). Для удобства _ссравнения В. в с переменным шагом их характеризуют так называемым условным шагом, к-рый вычисляется в сечении на радиусе 0,75 R, где R—радиус винта. Для удобства расчетов и обозначений очень часто воздушный винт характеризуют относительным шаг о’м h, относя величину абсолютного шага к диаметру данного воз-7 н душного винта, т. e. h=^.

Правыми называются В. в., вращающиеся по стрелке часов, если смотреть по направлению движения, левыми же— вращающиеся против часовой стрелки. В. в., установленный спереди самолета, называется тянущим, при установке же сзади, за крыльями (вернее, за мотором),—толкающим. Для обычных авиационных моторов, имеющих правое вращение, тянущие В. в будут правого вращения, а толкающие—левого.

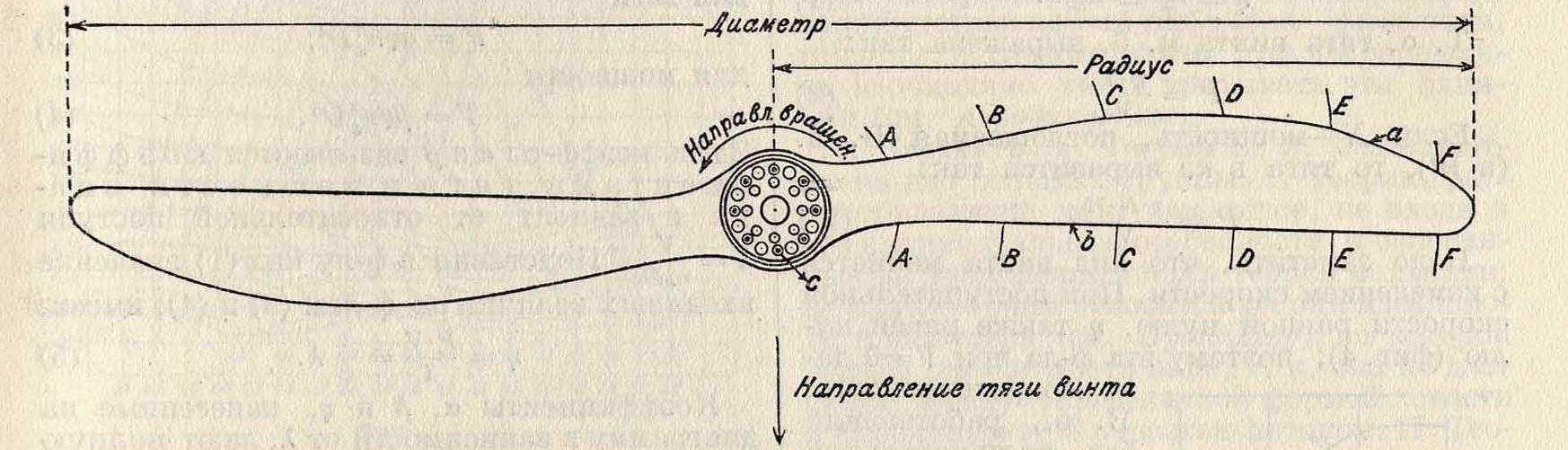
Другим элементом, характеризующим геометрич. формы винта, является ширина лопасти. Обычно форма лопасти такова, что ширина ее по радиусу переменна. Для сравнения подобных по форме винтов определяют относительную ширину лопасти, являющуюся отношением наибольшей ширины

к диаметру, то есть b—~.* * Размеры ступицы задаются по втулке данного мотора, к которому предназначается воздушный винт.

Перечисленные геометрич. характеристики определяют только общий характер В. в., более же полно его форма определяется помощью чертежа, на к-ром нанесены не только общие формы, но также и величина и форма сечений. В воздушных винтах лопасть вычерчивают в двух проекциях и на одной проекции, представляющей вид винта с его рабочей стороны, наносят сечения под углом, равным углу наклона лопастей. Обычно между шагом винта и поступью называется абсолютным скольжением:

S=н — н_а.

Обычно рассматривается не абсолютное, а относительное скольжение, отнесенное к шагу винта, то есть

„ _ Н-На _ ₁ Н_а^s--н “ ¹ Н~ ’

к-рое дается в процентах. В зависимости от типа аэроплана скольжение меняется в довольно широких пределах, начиная от отрицательного скольжения в несколько процентов до 40—50% у тихоходных аэропланов.

Диаметр

Радиус

//оправление теги винта

Ь

Фигура 3.

каждую лопасть делят на пять или десять частей и радиусы взятых сечений выражают в относительных единицах; это отношение называется относительным радиусом

XI

и обозначается г. Так. обр. эти относительные радиусы могут служить также вместо номеров сечений. Так как В. в имеют сравнительно узкие лопасти, то на чертеже обычно наносят сечения плоскостью, касательной к данному соосному цилиндру с относительным радиусом г, которые и вводят при теоретических расчетах.

Если представить себе винт ввинчивающимся в воздух, как в твердую гайку, то за один оборот он продвинется на расстояние, равное шагу И. Однако, вследствие податливости воздуха, винт за один оборот пройдет меньший путь. Если через V обозначить скорость движения В. в., а через щ—число его оборотов в секунду, то за один оборот он продвинется на расстояние Н_а=—, называемое поступью винта. Разность

_I

* В настоящей статье буквы, набранные жирным шрифтом, не обозначают векторов.

Если двигать винт со скоростью шага, то направление движения каждого сечения (в случае винта с постоянным шагом) совпадет с хордой сечений, то есть угол атаки сечения будет равен нулю; однако такое сечение все же будет иметь нек-рую подъемную силу, проекция которой на ось В. в составит некоторую тягу, и лишь при некотором отрицательном угле атаки эта проекция будет равна нулю.

Путь, пройденный винтом за один оборот при нулевой тяге, называется динамическим шагом винта H_d. Относя скольжение к динамич. шагу, получим динамическое скольжение:

Динамический шаг всегда больше геометрического. Скольжение и динамический шаг применяются в качестве характеристик при расчетах воздушного винта сравнительно редко. Относя поступь к диаметру винта, получаем относительную поступь ;.=, которая играет довольно видную роль при расчета винтов.

При вращении В. в., на которое тратится некоторая мощность Т (кгм/ск), создается сила тяги. Если при этом В. в движется со скоростью V(m/ck), то он, следовательно, отдает полезную мощность T_lt равную произведению силы тяги на скорость, то есть Т_г=Р· V. Полезная мощность всегда бывает меньше затрачиваемой на вращение, то есть поглощаемой, т. к. при превращении энергии имеются нек-рые потери—трение, вихре-образование и потери в отходящей струе. Отношение η полезной мощности к затраченной называется кпд В. в., то есть т, р-V

^η=Ύ⁼⁼~τ~ С¹)

Т. о. тяга винта м. б. выражена так:

Р-Ф (2)

Если N—мощность, поглощаемая В. в (в №), то тяга в килограммах выразится так:

Р=(2)

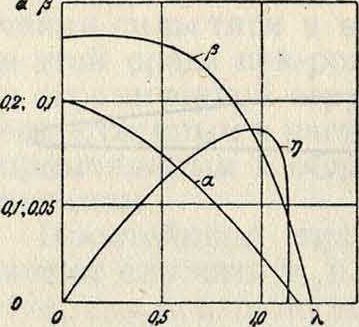
Надо заметить, что кпд винта меняется с изменением скорости. При поступательной скорости равной нулю, η также равен нулю (фигура 4); поэтому эта формула при F=0 да-tj ет неопределенность. В. в., работающий без поступательной ip скорости, называют работающим на месте, в отличие οί от гребного винта, имеющего поступательную скорость F. Для проверки теорий винта, а также для составления диаграмм, по которым можно было бы подбирать винты, производят испытания воздушного винта, разделяющиеся на две категории: испытание моделей и испытание в натуру. Как и при испытании крыльев, в настоящее время наиболее распространенным способом является испытание моделей В. в аэродинамической трубе. Испытание В. в натуру на аэроплане производится как при помощи некоторых искусственных методов, так и при помощи динамометрической втулки (смотрите), которая дает возможность находить в полете силу тяги и вращающий момент. При испытании модели последняя помещается в аэродинамическую трубу, причем измеряются мощность, потребляемая на вращение, тяга, скорость потока и число оборотов винта; число оборотов дают примерно такое, чтобы характеристика опыта (смотрите Аэродинамика) сохранялась б. или м. одинаковой, как и в большом винте. При этом необходимо вывести те зависимости, которые имеют место при переходе от модели к натуре, то есть выяснить закон подобия. Для перехода от модели к натуре необходимо, чтобы соотношение скоростей поступательной V и окружной U на соответствующих радиусах подобных винтов было одно и то же, то есть jj=Const. Окружная скорость на всех радиусах пропорциональна окружной скорости на конце лопасти:

Фигура 4.

U=2%Rn_s.

Таким образ, необходимо соблюсти условие

V V «

- Const,

: Я=Const,

U π-ns-D

ИЛИ

V

щ - D

то есть при переходе от одного винта к другому, ему подобному, необходимо, чтобы относительная поступь была одна и та же. Для охарактеризования работы подобных винтов слуя-сатт.н. формулы подобия, которые выводятся на основании правила однородности формул механики и имеют вид: для тяги

Р=αρη Ώ¹·, (3)

для мощности

Т=βρη^Ώ^. (4)

Здесь коэфф-ты аи β называются коэффициентами тяги и мощности винта и зависят от относительной поступи

Я =. Подставив в формулу кпд (1) значение входящих величин по ф-лам (3) и (4), имеем: η=-_Ύ-=_Ύλ. (5)

Коэффициенты а, β и у, нанесенные на диаграмму в зависимости от Я, дают полную картину действия данного винта (фигура 4). В некоторых случаях вместо мощности, потребной на вращение винта, рассматривают вращающий момент М, через который мощность выражается следующим образом: T=M-ii=M-2nn_a,

где Ω—угловая скорость вращения винта. Ф-ла подобия для момента будет иметь вид:

М =

p-p-ng--D^b

2 πη_β

= μρηΙΏ⁵;

здесь μ называется коэффициентом момента и выражается равенством:

^ р-

Иногда пользуются еще другой формой характеристики, вводя в ф-лы не число оборотов, а поступательную скорость F,именно: Р=ctj-ρ·!)²· F²

Τ=β₁·ρ·Ώ*·ν*.

Но эти формулы не так удобны для пользования, как первые.

Наиболее простой формой подбора В. в к самолету является подбор их по моделям, испытанным в аэродинамической трубе. Для наиболее рационального выбора следует иметь возможно большее число испытаний различных винтов. Это приводит к сис-тематич. испытанию т. н. семейств винтов, то есть ряда винтов, в которых изменяется какой-нибудь один параметр. Обычно за такой параметр принимают шаг винта,—тогда в семействе будут винты, сходные по своим формам, но имеющие разные шаги. Если шаг данного семейства по лопасти переменный, то для каждого винта семейства шаг изменяется на каждом сечении лопасти пропорционально. Для общности диаграмм за параметр семейства принимают обычно относительный шаг 7г. Характеристику всего семейства наносят на диаграмму в виде сетки, поперечные линии которой будут относиться к одинаковым кпд. По такой сетке можно подбирать В. в следующим образом. Имея задание подобрать винт с мощностью мотора

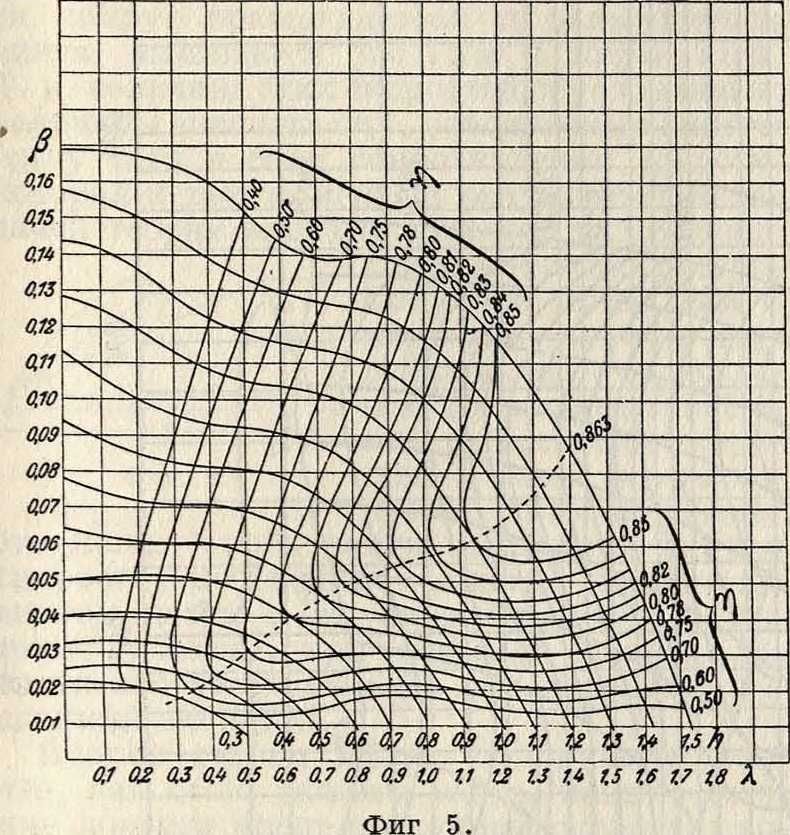
N 1Р, диаметром D м, числом об/м. п при скорости V м/ск, мы можем найти значения

β=—и λ=по диаграмме (фигура 5)

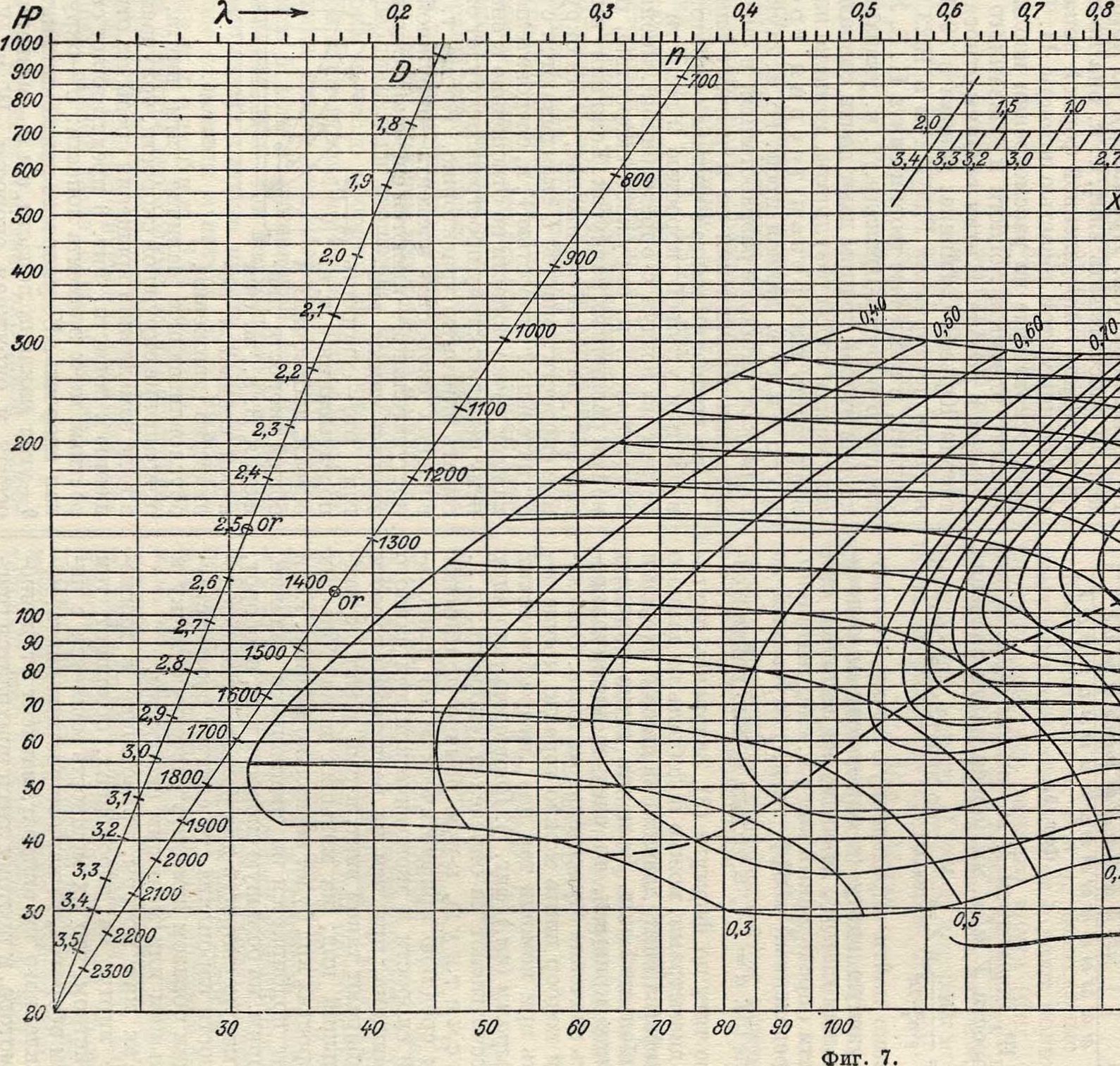
можно найти определенную точку, соответствующую винту (с определенным относительным шагом), дающему на заданной скорости определенный кпд η и, следовательно, определенный коэфф. тяги, получаемый по ф-ле (5): α= -р, а отсюда можно найти и самую тягу по формуле (3). Задаваясь другими диаметрами, можно подобрать из данного семейства винт, дающий на данной скорости наибольший кпд. Если эта точка попадает между кривыми, то следует интерполировать значение относительного шага. Описанный подбор винта можно гораздо проще делать при помощи так называемым логарифмических диаграмм (смотрите) (фигура 7). Первоначально винт рассчитывают на определен, скорость, т.н. расчетную, к-рую обычно принимают как среднюю арифметическую из наибольшей скорости и экономической для данного аэроплана, причем на расчетной скорости подбирают такой винт, к-рый давал бы наибольший кпд; на меньших и на больших скоростях кпд будет несколько меньше. Если винт подбирается на специальное задание, наприм. на большую скорость или, наоборот, на малую скорость для большей скороподъемности аэроплана, то следует соответствующим образом изменять расчетную точку к большим или меньшим скоростям.

Так как моторы, приводящие в движение винты на аэропланах, обладают тем свойством, что их мощность меняется с числом оборотов, то характеристика винта, поставленного на аппарат, зависит от данного мотора, и поэтому здесь приходится говорить о характеристике винтомоторной группы. Основной способ по строения этой характеристики дан в ст. Аэродинамика, Расчет самолета. Еще проще ее можно найти, пользуясь ло-гарифмическ. диаграммой семейства винтов, вычертив на отдельной кальке в том же масштабе значения мощностей, соответствующих различным ч оборотов. Ориентируя эту кальку так, чтобы расчетная точка соответствовала выбранному для нее диаметру, и передвигая ее по оси абсцисс (скорости), получим характеристику данного В. в и мотора. Обычно семейства В. в испытываются изолированными; на самом же деле воздушный винт почти всегда работает в присутствии какого-либо тела—фюзеляжа, гондолы, и, следовательно, при подборе винта необходимо уметь учитывать эти влияния (смотрите Аэродинамика).

I. Теории В. в Теории В. в разделяются на две больших группы: I. Теории, рассматривающие винт как целое, не входя в его индивидуальные особенности, и основанные на применении общих теорем механики; к таким теориям относится теория идеального пропеллера (смотрите Пропеллер), по которой нельзя рассчитывать винт, т. к. она не дает связи между определенной формой лопасти и вызванным этой лопастью потоком. II. Теории, основанные на рассмотрении изолированного элемента лопасти и вызванного им эффекта в потоке. К этим теориям относятся теория Юрьева-Сабинина, данная в 1911 году и после повторенная Глауертом в 1923 году в Англии, и вихревые теории винта Η. Е. Жуковского и Бетца-Прантля. Т. к. указанные теории второй группы дают почти совпадающие между собой результаты, то ниже изложена лишь вихревая теориягреб-ного винта, данная проф. Η. Е. Жуковским, как наиболее разработанная в смысле методики приложения ее к расчету винта.

При вращении винта с числом оборотов п₃в сек. или угловой скоростью Ω лопасти набегают на воздух с определенной линейной скоростью, т. н. окружной скоростью, разной на различных радиусах. Если винт имеет еще поступательное движение, то эти окружные скорости лопастей U складываются с поступательной скоростью V, и, следовательно, каждая точка лопасти по отношению к внешнему неподвижному пространству будет описывать винтовую траекторию. Кроме т. н. внешних скоростей элемента—окружной и поступательной—имеются еще скорости, вызванные самим винтом: это —· скорость подсасывания ν, то есть осевая,добавочная к общей скорости движения В. в., за счет которой создается количество движения, обусловливающее наличие тяги винта, и приращение окружной скорости, получаемое в виде замедления вращения среды по отношению к лопасти, Фигура 6 представляет ско-ростный мн-к элемента лопасти: U—окружная скорость, V—скорость движения Винта, 8—угол наклона лопасти,?; и и—вызванные осевая и окружная скорости, W и W₁— кажущаяся и действительная относительные скорости. При работе винта на месте

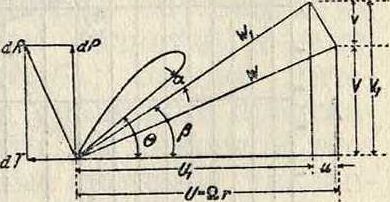
ФИГ. 6.

Фигура 8.

поступательной скорости винта V совсем не будет, и останется только скорость подсасывания V (фигура 8).

Та конфигурация скоростей, которая имеется вокруг вращающегося и движущегося винта, называется полем скоростей. Т. к. величина этих скоростей обусловливает величины внешних сил, развиваемых винтом (силу тяги и силу сопротивления лопасти, которая и дает момент на валу винта), то задачей теории винта и является нахождение для данного винта поля скоростей, а по ним и внешних сил, а, с другой стороны,—нахождение по заданным внешним силам поля скоростей и такой формы лопастей, которая создает это поле. Чтобы найти вызванные винтом скорости, необходимо связать вызванный винтом поток с его лопастями, то есть найти такие условия, при которых каждой лопасти соответствовал бы определенный вызванный ей поток.

Вопрос теории винта усложняется тем, что, как было указано выше, каждое сечение лопасти имеет различные скорости; поэтому приходится рассматривать отдельно движение каждого элемента лопасти, получаемого, если рассечь лопасти винта двумя близкими соосными цилиндрами с радиусами г и r+dr, находить вызванный каждым элементом поток и потом интегрировать по всем элементам. Рассматривая каждый элемент лопасти, приходится уподоблять его элементарному крылу, имеющему скорость W по отношению к внешней среде. Такое крыло будет давать как подъемную силу, так и лобовое сопротивление, которые находят экспериментальным путем (смотрите Аэродинамика). С другой стороны, можно найти вызванный винтом поток или на основании общих теорем механики или рассматривая поле скоростей, вызванное той системой вихрей, которую создает вращающийся винт. Приравнивая в том и в другом случае соответствующие, выраженные ф-лами, величины, характеризующие поток, можно получить ур-ие связи лопасти с потоком. Так. обр. теории В. в все же опираются на эксперимент, так как охватить сопротивление крыла в потоке полностью теоретически пока не представляется возможным. Т. к. элемент лопасти рассматривается бесконечно узким, не имеющим свободных концов, а работающим лишь как часть крыла, то работа такого элемента будет аналогична работе его в плоскопараллельном потоке, и поэтому сопротивление этого элемента надо брать, как для соответствующего крыла бесконечного размаха (смотрите Индуктивное сопротивление). На этот элемент будет действовать некоторая сила сопротивления dR, которую можно разложить на две составляющие: по оси—dP, элементарную силу тяги, и по перпендикулярному к ней направлению—dT, элементарную силу сопротивления. Умножая последнюю на соответствующий радиус г, получим момент на оси от этой элементарной силы. Интегрируя по всей лопасти, можно найти полную тягу и момент.

В основу вихревой теории гребного винта взято положение, что скоростное поле вокруг вращающегося и движущегося винта управляется вызванными лопастями вих jhmh присоединенными,!, е. идущими по лопасти, и свободными, исходящими из присоединенных и движущимися в потоке за винтом. Эти вихри образуются за счет разности скоростей в двух смежных сечениях лопасти. В общем случае с лопастей винта сходит вихревая пелена, которая образует в струе винта поверхность, близкую к винтовой. Внутри лопасти винта эти вихри идут в виде воображаемых, т. н. присоединенных вихрей, которые замыкают т. о. появляющиеся на лопастях свободные вихри и далее переходят в вихревой столб, идущий по оси винта. Т. о. при рассмотрении поля вокруг винта можно совершенно не принимать в расчет лопасти винта и считать, что в среде имеются лишь одни вихри (фигура 9). Свободные вихри, при известных соотношениях своих параметров, будут стационарны, и можно доказать, что они будут направлены по линиям токов относительного движения.

Исследовать влияние вихрей на скоростное поле можно двояким путем: или в относительном движении лопасти находить и с-тинные, вызванные вихрями, скорости или, рассматривая вихри в абсолютном или относительном движении, находить вызванные средние скорости (смотрите Вихревая теория). Первая задача представляет большие трудности и пока, по-видимому, полностью еще не решена. В СССР проф.

Фигура 9. Фигура ю.

Юрьев сделал попытку исследовать винт в относительном движении и найти истинные скорости, исходя из действия системы двух вихревых усов по концам лопастей и центрального вихревого столба; однако интегрирование полученных уравнений представляет большие трудности. В вихревой теории находятся вызванные системой указанных вихрей средние скорости потока. Т. к. вихревые шнуры как присоединенные, так и свободные при вращении винта становятся в различные положения относительно внешнего пространства, то задачу о нахождении поля можно свести к действию ряда вихревых слоев и вихревого донышка, причем, вследствие малого промежутка времени, протекающего между прохождением двух смежных вихревых шнуров (в особенности при многолопастных винтах), движение можно считать установившимся (фигура 10).

Скорость потока за винтом получает полное свое приращение вдали от винта, в плоскости же винта получается только половина этого приращения (смотрите Пропеллер). Таким образом струя за винтом получается сжатой, и поэтому упомянутые выше вихревые слои имеют форму некоторых поверхностей вращения, переходя, однако, за винтом в цилиндрический поток. В виду того, что для гребных винтов сжатие струи сравнительно невелико (наибольшим оно будет при работе винта на месте) и поток сравнительно быстро переходит в цилиндрический, влияние же удаленной части вихрей также невелико,—можно приближенно принять, что поверхности вращения вихревых слоев, образованных рядом вихревых шнуров, суть цилиндрические поверхности (фигура 11). Этим значительно упрощается весь математический анализ явления.

Задавая то или иное распределение циркуляции вдоль лопасти, мы будем получать соответственные интенсивности цилиндрич. вихревых слоев, а следовательно, и определенное в каждом случае поле средних скоростей. В данной теории рассматривается влияние каждого цилиндрич. вихревого слоя, вихревого донышка и центрального вихря, и находятся вызванные ими средние скорости. При циркуляции, постоянной вдоль лопасти, имеется лишь один вихревой цилиндрический слой с радиусом, равным ра-фигура и. диусу винта; этот слой вызывает определенную осевую скорость в потоке винта (постоянную по радиусу). Для упрощения формул вихревой теории вводятся т. н. отвлечен н ы е обозначения, а именно: для радиуса г=_R,

у для скорости потока V=^, для циркуляции •Г=,. для ширины лопасти Ь=’ Для тяги винта Р=----- ^-=пг, для мощности, по-

ZK· 0 · ii · Л

Т

глощаемсй винтом, Т=₂π·ρ.Ω³.1Γ⁵*

Согласно выводам вихревой теории, вызванные винтом скорости выражаются след, образом (фигура 6):

окружная и=^; (6)

•осевая скорость ν находится из следующего уравнения:

1

v(V+v)=J-(l~^j) + 2^_s^dr. (7)

Последний член учитывает влияние центробежных сил; поправка эта очень невелика, и можно с вполне достаточной для практики точностью этот член совершенно отбросить. Больше того, для целей практики можно принять следующую формулу для нахождения скорости ν:

v(V+v)=J(l -J),

Эта формула является точным решением уравнения (7) для случая постоянной циркуляции по лопасти. Ур-ие связи лопасти с потоком получается путем связывания циркуляции с характеристиками лопасти—шириной и коэффициентом подъемной силы—и имеет вид: J=G_y-b-W_t. (8)

Это ур-ие получаем,приравнивая выражение подъемной силы по теореме Жуковского выражению подъемной силы по обычной формуле, через абсолютный коэффициент С_у(смотрите Аэродинамика).

Элементарная сила тяги и мощность, потребляемая элементом сечения лопасти, найдутся из следующих соображений. По теореме Жуковского, распространенной им на случай кольцевого потока, подъемная сила, то есть сила, перпендикулярная направлению скорости, получается умножением циркуляции на плотность и на среднюю геометрич. скорость подходящей и отходящей от лопасти струи; направление этой силы находится, если повернуть вектор этой скорости на прямой угол в сторону, обратную циркуляции. Лобовое сопротивление профиля (профильное сопротивление) можно найти опытным путем:

7*- — pH у ·

Спроектируем подъемную силу профиля и лобовое сопротивление на два направления: на ось винта и на касательную к окружности. Компоненты первой силы найдутся, если отнести ее соответственно к скоростям XJ_x и V_х:

2_e7T/j dr и 2JV_xdr.

Принимая во внимание предыдущее равенство, найдем:

“=bТ (ТТ, - pVj)

И

do

~ — 2J (Fj + μΤΙj),

или

= 2,7 (b - рГ_х) (9)

И

^=2 JT(r_x+pUJr, (10)

где dT—элементарная мощность, поглощаемая винтом. Кпд будет выражаться т. о.:

У-dr _Vj- _ Г

dT ~ Г,+ μ-Ρ·, г

(11)

при чем μ=-_с^р, где С_р—профильное сопротивление данного сечения или, что одно и то же, лобовое сопротивление дужки, соответствующей бесконечному удлинению. Формулы (9) и (10) м. б. заменены обычными коэфф-тами, выражающими работу гребного винта (смотрите выше), то есть:

, _ da_ di Р _ π* (ίΡ

^a dr dr p·n*-D⁴ 2 dr

_Rf d3 d f T rS dT

P ~ dr — dr ο·η*·Ι)⁵ 2 dr

где λ== n-Г. Подставив сюда значение

dP dT _

для и tT, получим:

a=π³· (?,·& -TF?·cos/?(1 - μ tgfi), (12) β=n^Cy-b-Wf-r-siη/9(1 + ,uctg/?), (13)

(7)

или, так как

W₁=W · cos Δα=г

COS Δα COS γ

β=π⁴· Су.b.г».^ · sin /9(1 + μ ctg /9),

_ + _ _χ _ 1 - μ-tgp _ tgj _

‘^r Ρ " 1 + μ-ctgp ‘ tgp ‘

винта. Поверочный расчет по номограмме (фигура 12) делается следующим образом. Из чертежа винтам, б. найдены: 1)Δ ₌ Π-; 2) от-

6

носительная толщина сечения лопасти с=;

3) угол наклона лопасти (фиг .7)6=arc tg где h—высота подъема лопасти. Для каждо-

у χ

го радиуса находим: у=arc tg —=arc tg—.

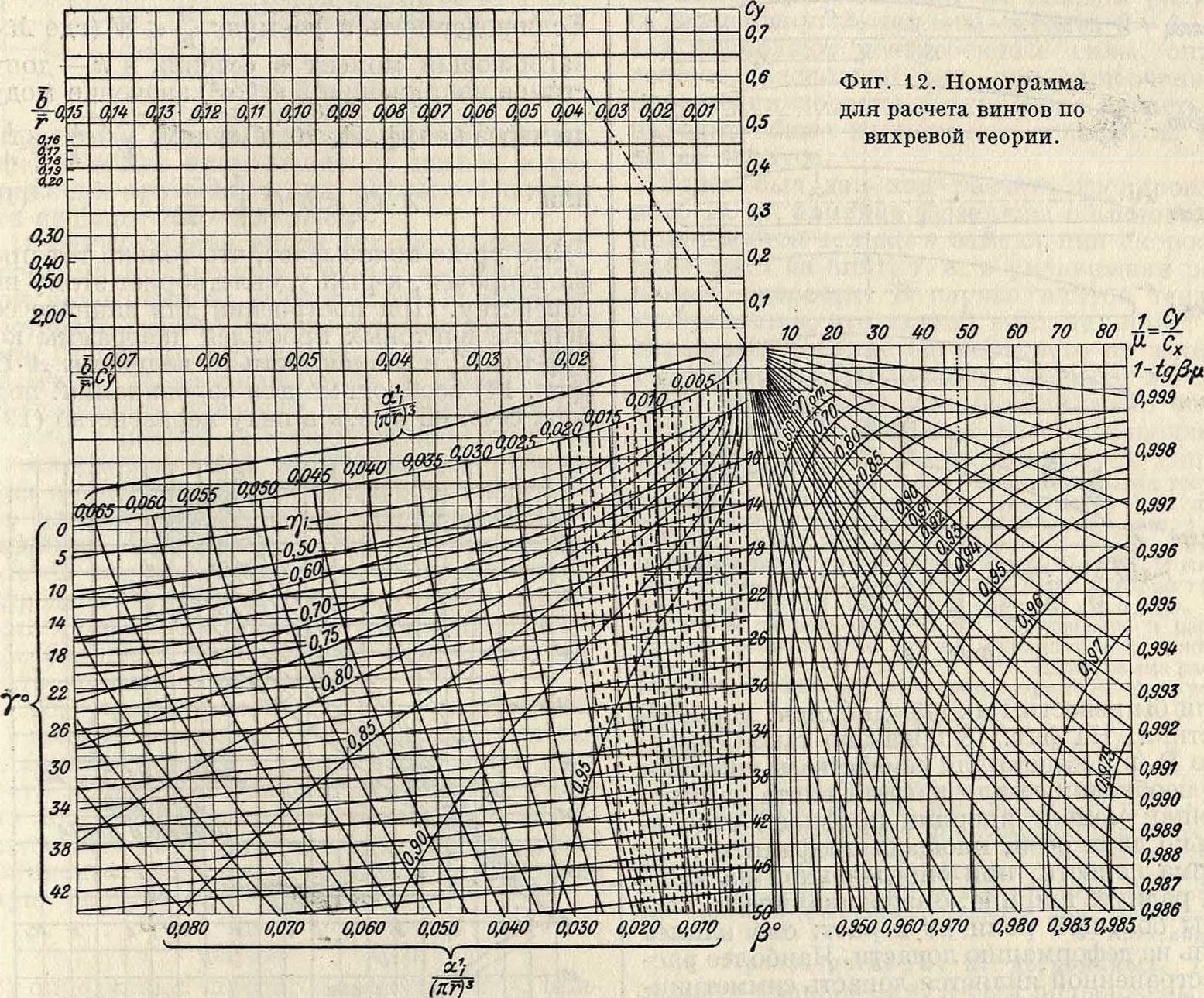
Для идеального случая, когда μ=О, будем иметь:

<=л³-С,_&._г2.^!А^а. cos β,

г у cos γ *

β=п“-С_у-b-г“-^с^ sin β=π-r-a/-tg β,

г, =ίϋ.

^Iri tg β

ИЛИ

α= <“,·( 1 —μ tg β), (14)

β=/9/(1 + μ Ctg β) =

= j[i*-«/-tg/9(1 + ft ctg/9), (15)

П_т=Чщ-П_Гоп, (16)

1 - μ- tg ρ

^{ГД Пг}от.~ 1+K-CtgP

При помощи ф-лы (15) и пользуясь специально составленными номограммами (предложенными Г. Кузьминым), можно чрезвычайно быстро произвести расчеты винтов—как поверочные на все режимы работы, то есть для разных λ (смотрите выше), так и расчет нового

Имея характеристику сечения {С_у в функции а) для бесконечного удлинения, начерченную на прозрачной бумаге, находим по номограмме η_η, Цг_т. и (1—/tttg/9) след, образом: 1) проводим в верхнем левом углу прямую, пользуясь масштабом “; 2) путем проб находим угол атаки а профиля, задаваясь сначала этим углом и соблюдая условие « + /9=6, причем угол β находится по нанесенному на номограмме масштабу. Для найденного угла атаки находим по номограмме величины ητ_{, а по аэродина мической характеристике данного сечения и значение —=^. По найденному уже углу β

Н· Ср и значению Δ находим из правой стороны диаграммы значения Пг_от. и {1—μΧ$β). Т. о. можно вычислить величины:

= (ην) -μ tg β),β=~ И Vr=Пп-Пгот.

8

Т. Э. m. IV.

Определив для нескольких радиусов эти величины, можно построить диаграммы, найден-. ных. величин цо г и т. еле интеграции уравнений этих кривых получить общую тягу и мощность, а также и общий кпд всего винта по формуле η ~ -у^-.

Чтобы спроектировать В. в., необходимо иметь семейства винтовых профилей, у к-рых

У

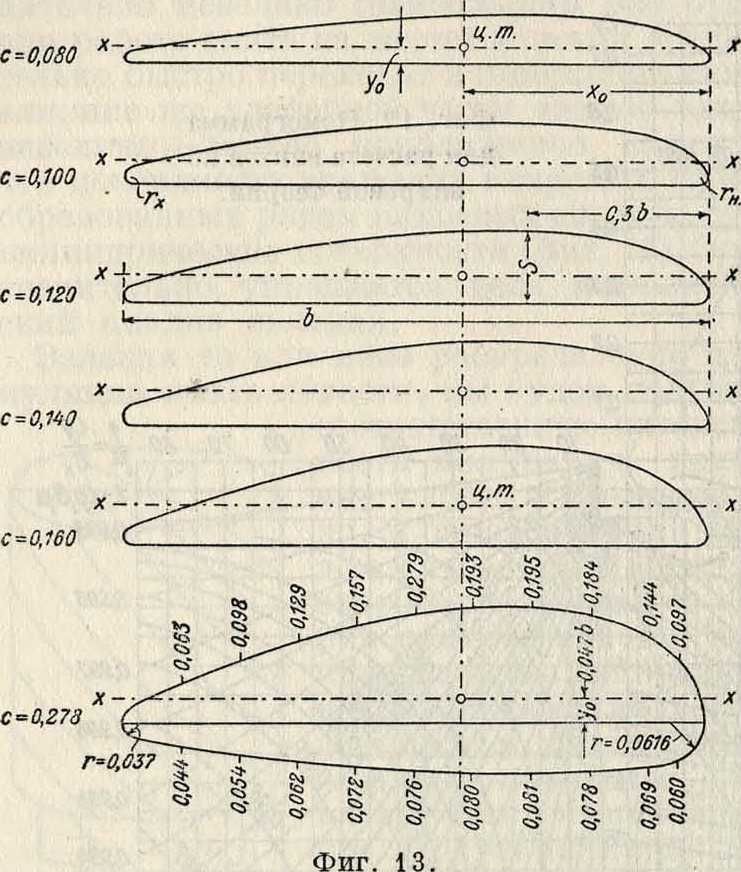
были бы известны их аэродинамич. характеристики. На фигуре 13 показано такое семейство В. в Обычно для семейства вычисляют все необходимые для расчета винта данные, именно: момент инерции профилей относительно двух осей, площадь профиля и тому подобное. Форма лопасти, при определенной на каждом радиусе ширине, с аэродинамическ. стороны большой роли не играет; она влияет лишь на деформацию лопасти. Наиболее распространенной является лопасть симметричной формы или немного откинутая в сторону вращения или в обратную сторону.

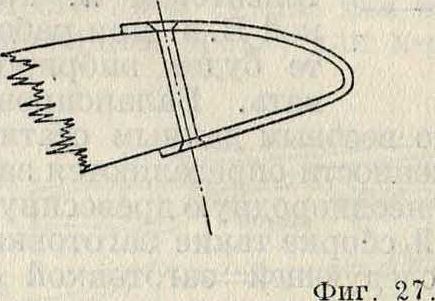
Расчет винта на прочность играет видную роль в проектировании винта, так как материал его бывает всегда сильно нагружен. Особенностью этого расчета является зависимость качеств винта от его прочности; поэтому при проектировании винта приходится, из-за требования прочности, ставить некоторую границу в повышении качества. Следовательно, аэродинамич. расчет винта тесно связан с расчетом его на прочность. Т. к. момент около оси наибольшей жесткости играет малую.роль в расчете винта, то можно принять (фигура 7), что винт изгибается только силой, нормальной к оси наименьшей жесткости; приближенно за эту силу можно принять силу тяги; тогда на каком-нибудь радиусе а коэффициент изгибающего момецта выразится так:

1

2г-М„ п

= J (^r~^a) ^adr> (¹⁷)

a

а изгибающий момент на радиусе а для каждой лопасти будет:

1

М_а=J (r-a)adr, (18)

а где i—число лопастей.

Модуль сечения винта Wм. б. представлен в таком виде: W=(-у )³> где А—некоторый коэфф., зависящий от очертания профиля, а Ь — ширина лопасти в данном сечении.

Если подставить в формулу^ i W (где М—

изгибающий момент в сечения и к — допустимое напряжение в килограммах/см“) значение модуля через коэфф. А, то получим: М ^ А,

или A-C^b-C^p^J- (¹⁹>

Это ур-ие показывает, что только тот профиль прочен, к-рый удовлетворяет этому неравенству. При построении для данного семейства винтовых профилей диаграммы ко-эфф-тов С_у в зависимости от величины А C_v(фигура 14) необходимо для аэродинамич. подбора сечений иметь в виду неравенство (19).

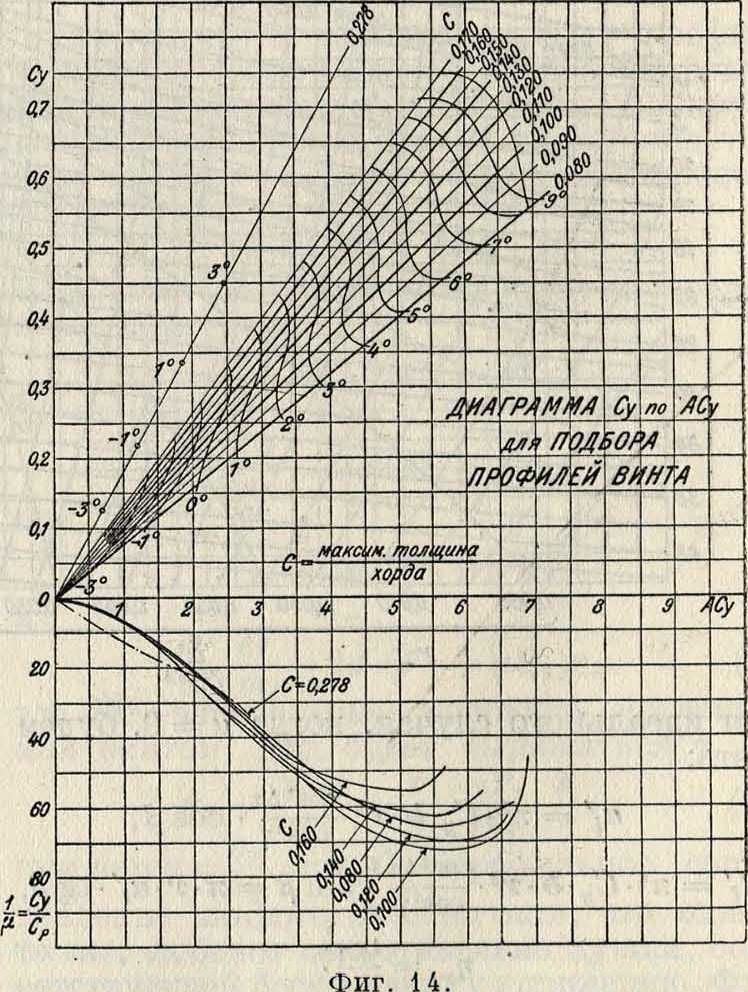
Подставив в него значение b, через отвлеченные его обозначения, получим:

Л-СИт

(190

Кроме изгибающих сил на лопасть действует еще центробежная сила, которая на радиусе а равна

и напряжение от центробежных сил будет

S З’Г dr U². А."_

’ а ®а

У а —

По большей части центробежной силой пользуются в качестве разгружающей силы изгиба лопасти. Если лопасть винта откинута немного вперед (по направлению движения винта) от плоскости вращения основания лопастей у ступицы (фигура 15), то от центробежных сил появляется некоторая составляющая с1В₃, противоположная элементарным

Фигура 15.

силам тяги dP. В деревянных воздушных винтах общее напряжение от изгиба и растяжения принимают для расчетной скорости не более 250—300 килограмм/см².

Проектирование винта (кроме расчетных операций, сильно упрощенных вышеуказанной номограммой) выражается: 1) выбором соответствующего распределения циркуляции; 2) подбором дужек на соответствующем радиусе, удовлетворяющих условию (19); 3) приданием лопастям винта определенной формы в плане; 4) вычерчиванием винта и сглаживанием всех получившихся неплавных переходов, однако таким образом, чтобы не изменить значительно первоначального задания. Обыкновенно после проекта делается еще поверочный расчет винта, чтобы определить, насколько в периоде проектирования пришлось отойти от задания. В случае большого расхождения приходится делать некоторые поправки.

Ход проектирования В. в следующий:

1) выбрав расчетную скорость винта и задавшись диаметром (наивыгоднейший диаметр лучше всего находить предварительно по логарифмическим диаграммам серий испытанных винтов), находят значение коэффициента мощности β мотора и относительную поступь λ:

о 75JV, У.

^р p-nJ-D·’ n_s-D’

2) определяют предполагаемую тягу, приближенно находя кпд вилта по формуле 4=VrVom., где VI—·идеальный, а ^—относительный кпд, выражающиеся ф-лами:

Vi=~

ⁱ⁺V ^ι+τ·Λ

1- 2μ i+r-μ···

τ,|·π.

коэфф. μ можно принимать равным 0,03— 0,04; по этим формулам значения находят путем проб, задаваясь различными значениями η; 3) по найденному η находят α= ~;

4) задаются каким-либо законом распределения циркуляции по лопасти, обычно постоянным (это тип В. в НЕЖ) или эллиптическим; 5) распределяют тягу по лопасти, приближенно определяя значение элементарной тяги на каждом радиусе по формуле:

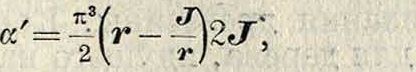
однако так. обр., чтобы .общая тяга равнялась найденной в п. 3; 6) вычисляют значение и у=arc tg “з для каждого радиуса;

7) находят по номограмме значения ^ С_у, β и tj_r.; 8) вычисляют по формулам (17) и (18)

г и Ж_а на каждом радиусе, а также и напряжение 1с; 9) подбирают на каждом радиусе дужки из серии таким образ., чтобы удовлетворить найденному в п. 7 значению 4 С_у,

а также и неравенству (19) (фигура 13), то есть находят значение Ь ширины лопасти и угла атаки, к; 10) находят на каждом радиусе значение угла наклона лопасти θ=β + α; 11) вычисляют центробежные силы, определяют, насколько они при вычерченном положении лопасти разгружают лопасть, и находят общее напряжение лопасти на каждом радиусе.

Здесь был дан ход расчета изолированного В. в.; влияние фюзеляжа обыкновенно принимается только в замедлении скорости набегания на винт, то есть в уменьшении расчетной скорости. В случае винтов тендем принимается, что задний винт не влияет на передний, влияние же переднего на задний выражается в увеличении скорости набегания. Эта скорость или приближенно определяется по теории идеального пропеллера или находится из расчета переднего винта.

Лит.: Жуковский Η. Е., Вихревая теория гребного винта, «Труды Отд. физ. наук О-ва люб. ест., антроп. и этнографии», М., 1912, т. 16, вып. 1.М., 1914—15, т. 17, вып. 1—2; Юрьев Б. Н., Возд. гребные винты (пропеллеры), «Труды ЦАГИ», Москва, 1925, вып. 10; В е т ч и н к и н В. IX., Теория гребных винтов, М., 1926; Александров В. Л., Вихревая теория лроф. Η. Е. Жуковского и расчет по ней гребных возд. винтов, «Техника возд. флота», М-, 1928, 3; Кузьмин Г. И., Номограмма расчета гребного винта по «вихревой теории» Η. Е. Жуковского, там же, 1927, 2, стр. 95; П р о с к у р а Г. Ф., Возд. винты, Харьков, 1927; Watts Н. С., The Design of Screw Propellers, L., 1920; Park W. E., A Treatise on Airscrews, L., 1920; Fage A., Airscrews in Theory’ and Experiment, Edinburgh, 1920· H e 1 m b о 1 d H., Die Betz-Prandtlsche Wirbeltheo-rie d. Treibschraube und ihre Ausgestaltung z. techni-schen Berechnungsverfahren, «Werit, Reederei. Hafen» Berlin, 19.26, .Tg. 7, Η. XXIII. XXIV; GlauertH.’ An Aerodynamic Theory of the Airscrew, «Aeronautical Research Committee, Reports and Memoranda», London, 1922, 786. в Александров.

И. Производство В. в деревянных. Громадные напряжения, которым подвержены лопасти В. в., а также зависимость его кпд от точности выполнения, предъявляют к производству особые требования, которые должны гарантировать: 1) достаточную крепость В. в.,

2) неизменяемость его формы, 3) статич. и динамическую уравновешенность, 4) точность обработки. Первое достигается применением лесных материалов, обладающих высокими технич, качествами и имеющими коэфф. крепости на изгиб не ниже 700 килограмм/см² и на сжатие не ниже 400 килограмм/см². Помимо этого, дерево, идущее на изготовление В. в., должен быть прямослойным, абсолютно здоровым, без сучьев и трещин. Наиболее широкое применение имеют красное дерево, орех, ясень, клен, красный бук; реже применяются дуб, ольха, карагач. Не исключается возможность применения и др. пород дерева, удовлетворяющих технич. требованиям, предъявляемым к авиационной древесине. Деревянный В. в., как и всякое изделие из дерева, имеет тот недостаток, что под влиянием атмосферной влажности в нем может произойти коробление лопастей, вследствие чего появляются

*8

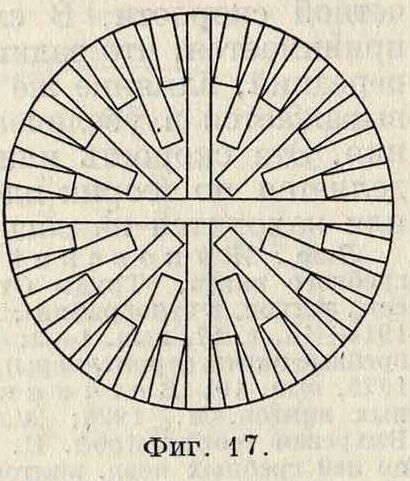
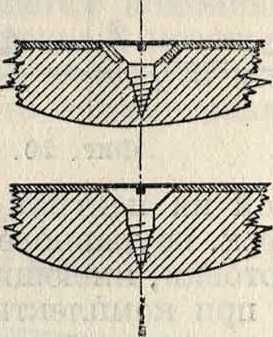
в работе вибрации, нарушающие плавность работы мотора и вызывающие опасные напряжения в частях самолета; для устранения этого в процессе производства принимается ряд мер, предохраняющих В. в от коробления. Сюда относятся: 1) применение досок, подверженных меньшему короблению, а именно: досок, расположенных ближе к сердце-вине кряжа а (фигура 16) или выпиленных радиально (фигура 17); но ради-альнаяраспиловка в применении кпроизвод-ству В. в целесообразна только при больших диаметрах кряжей (400 миллиметров и выше), вообще же дает малый процент выхода пиленого материала и обходится дорого, почему в винтовом производстве и не получила широкого применения; 2) склейка В. в из досок толщиной от 10 до 25 миллиметров; теоретич. возможность почти полного устранения коробления соответствующим подбором и расположением досок, имеющих стремление коробиться в разные стороны (фигура

18), практически неосуществима; 3) выдержка полуфабрикатов В. в производственных помещениях с целью придать им равномерную влажность; 4) предохранение В. в от поглощения атмосферной влаги путем лакировки поверхности дерева и покрытия водонепроницаемым составом всех дыр, просверленных в винте.

П р о и в о д с т в е н н ы и п р о ц е с с. 1) По рабочему чертежу определяются минимальные размеры отдельных досок, необходимые для получения соответствующего профиля в каждом сечении винта (фигура 19). К теоретически определенным размерам прибавляется от 5 до 15 миллиметров по ширине и до 100 миллиметров по длине (запас на обработку), и по таким шаблонампро-изводится разметка досок и выпиловка. Такой метод заготовки полуфабрикатов позволяет сократить дальнейшую обработку и увеличить пропускную способность сушилок. В целях рационального использования материала допускается как долевая, так и поперечная склейка отдельных досок, причем число досок, имеющих поперечную склейку, должен быть не более трех на винт, при обязательном чередовании с цельными досками. Поперечное сращивание делается в поддерева. В раз-метку может идти лишь отборный испытан-йый материал, удовлетворяющий во всех отношениях «техническим условиям». При разметке направление волокон древесины должно располагаться параллельно осевой линии В. в., имеющейся на каждом шаблоне.

2) Сушка. Долгое время считалось, что наивысшие технические качества, а также наименьшую склонность к короблению, имеет лесной материал естественной сушки, но длительность этого процесса (5—6 лет), требующая громадных оборотных средств, заставила обратиться к научному исследованию и усовершенствованию процессов искусственной, интенсивной сушки дерева. В современных усовершенствованных сушилках, при продолжительности сушки от 8 до 25дней (в зависимости от породы, первоначального состояния и размеров заготовки), возможно получить материал с влажностью 8—13% (допускаемая влажность при производстве В. в.). Тем не менее технич. качества (в отношении хрупкости и коробления) материала, пропускаемого через сушилки непосредственно после распиловки, ниже, чем у материала естественной сушки, и поэтому при производстве В. в применяется комбинированный метод сушки: не менее 6 месяцев естественной сушки для всех пород (за исключением ореха, для которого естественная

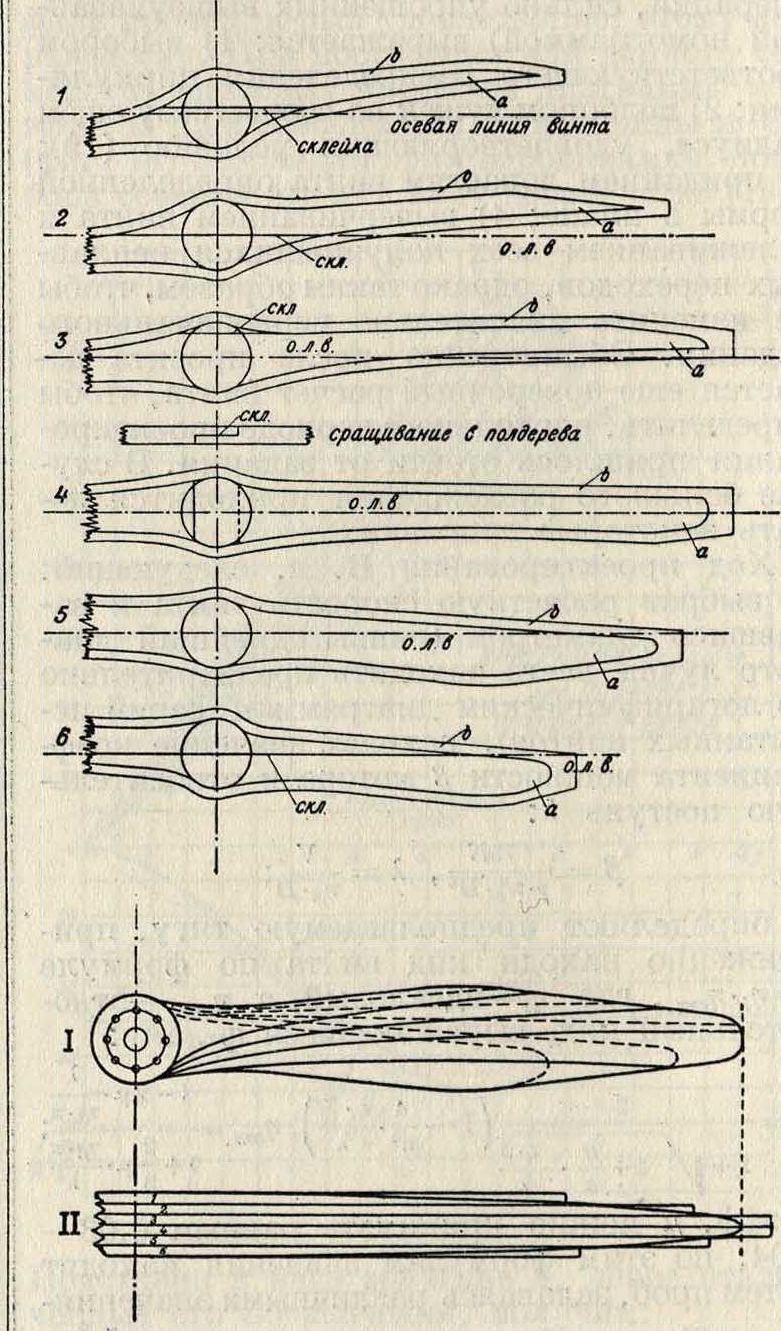
Фигура 19.

сушка должен быть не менее 12 месяцев) и последующая искусственная сушка. Для естественной сушки как территория лесного склада и сушилки, так и метод укладки материалов должны обеспечивать равномерную сушку и гарантировать невозможность заражения и загнивания древесинь!. Конструкция сушилок для дерева, идущего на изготовление воздушных винтов, должна допускать самую широкую регулировку режима сушки в отношении температуры, влажности и скорости циркуляции воздуха (смотрите Сушилки).

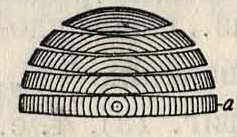
Фигура 18.

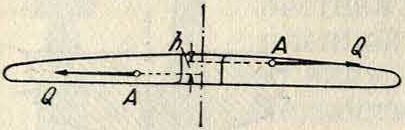
3) Пропущенные через сушилки заготовки выдерживаются в производственном помещении в течение 7 дней для того, чтобы влажность материала уравнялась с влажностью помещения, выстрагиваются до толщины, указанной на чертеже, с точностью ±0,1 миллиметров, сортируются с отбраковкой дефектных заготовок и поступают на комплектную сборку и балансировку на центрах; последняя операция весьма существенна, т. к. имеет целью достижение динамич. уравновешенности винта, которая получается только в том случае, если центры тяжести лопастей располагаются в одной плоскости. При неоднородном материале возможны расположение центров тяжести А, как указано на фигуре 20, и действие центробежных сил Q с эксцентриситетом b. Такой В. в при работе будет вибрировать. Балансировкой на центрах по весовым данным стати-ческ. неуравновешенности определяются заготовки, имеющие неоднородную древесину, и при комплектной сборке такие заготовки компенсируются следующей заготовкой с аналогичной неуравновешенностью противоположной лопасти.

4) Скомплектованные заготовки выверяются, цинубятся и поступают в склейку, при которой должен быть соблюдено правильное относительное расположение отдельных заготовок и совпадение всех осевых линий. Склейка производится горячим способом (с подогревом заготовок на паровых плитах или в специальных камерах) желатиновым клеем высшего качества, выдерживающим при испытании на скалывание не менее 100 к г/см² и не понижающим крепости склейки при размачивании в воде склеенных образцов в

Фигура 20.

Фигура 21.

течение 30 ч. при t° 15° более чем до 65 %. Чистый желатиновый клей удовлетворить требованиям водоупорности не может, и последняя достигается химическими примесями, составляющими секрет фирм, выпускающих специальные сорта клея. Удовлетворителен для склейки В. в герман. клей марки «Нахтигаль». Склеенный В. в прессуется в струбцинах или в специальных прессах в течение 24 ч. Давление пресса должен быть около 1,5 килограмм/см². После склейки до пуска в следующую операцию выдержка должна быть не менее 10 дней.

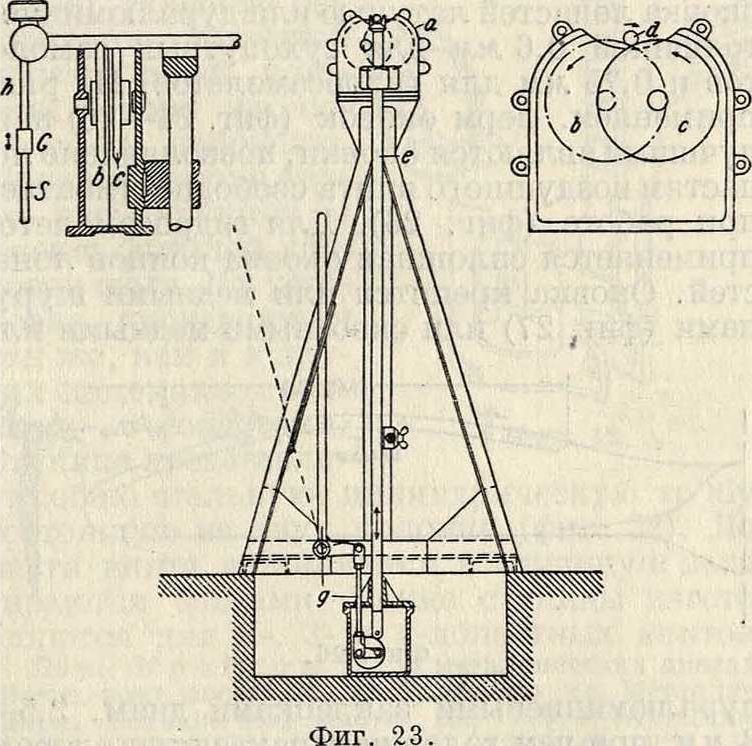
В последующих операциях производится постепенная обработка В. в с применением нижеследующих шаблонов, обеспечивающих точность выполнения винта по чертежу: 1) шаблон для фрезировки кромок, который в точности соответствует общему виду, вин та в плане; 2) шаблоны для обдирки винта на копировальных станках (фигура 21), выпускающих винты с припуском в 1,5— 2 миллиметров; 3) шаблоны профилей винта в 5—6 контрольных сечени ях, к-рыми руководствуются при ручной окончательной обработке винта (фигура 22); 4) боковые шаблоны для разметки и проверки правильн. положения кромок винта относительно горизонтальной плоскости. От правильности профилей и положения кромок зависит шаг В. в.; здесь разрешается допуск +2%, и поэтому операция окончательной обработки В. в должна производиться с особой тщательностью. Для достижения статической балансировки винта, проверяемой на чувствительном балансирном станке, разрешается снимать стружку до 1,5 миллиметров по всей длине лопасти с нерабочей стороны. Балансирн. станок (фигура 23) состоит из следующих частей: а—корпус для укрепления роликов; b и с—ролики; cl·—ось, на которой монтируется винт; е—вспомогательная штанга для плавного опускания винта на ролики; д—эксцентриковый механизм для

Фигура 22.

опускания винта; Τι—рычаг; G—передвижной груз для балансировки винта; S— стрелка для выверки симметричности лопастей.

Выбалансированяый винт поступает в лакировку, причем разрешается любой метод лакировки, выдерживающий следующие испытания: диск 0 150 миллиметров, толщиной 25 миллиметров. с закруглен, краями (радиус закругления 12,5 миллиметров), изготовленный из того же дерева, что и винт, лакируется по методу, принятому для производства, и, точно взвешенный,

погружается в воду на 8 дней; через каждые 24 часа образец взвешивается, и к концу восьмого дня его вес не должен увеличиться более чем на 2,5 г, что соответствует 6 мг

на 1 см². Один из удовлетворительных способов лакировки следующий: В. в олифится, загрунтовывается мастикой, кроется масляным лаком, шлифуется, затирается спир-• товой смесью шеллачного лака с политурой и вторично покрывается масляным лаком. Междукаждой операцией лакировки должен быть достаточный интервал для сушки. Общая продолжительность лакировки ок. 10 дней.

Для предохранения кромок винта от повреждения брызгами воды (у гидросамолетов и при полетах во время дождя) и песком или комьями земли и снега (при разбеге перед взлетом и при посадке) производится

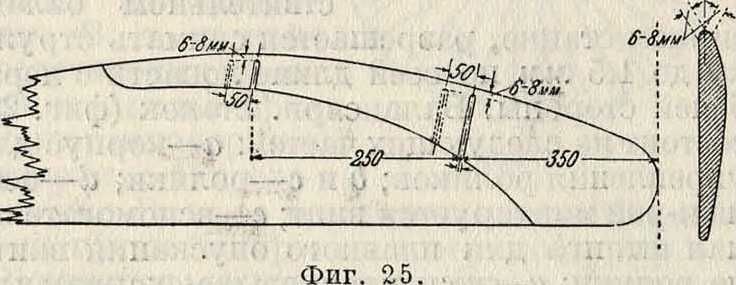
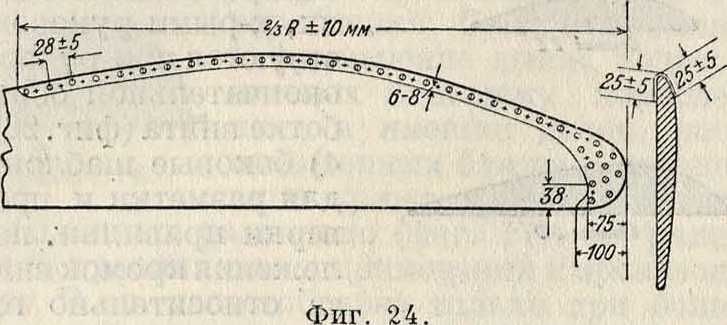
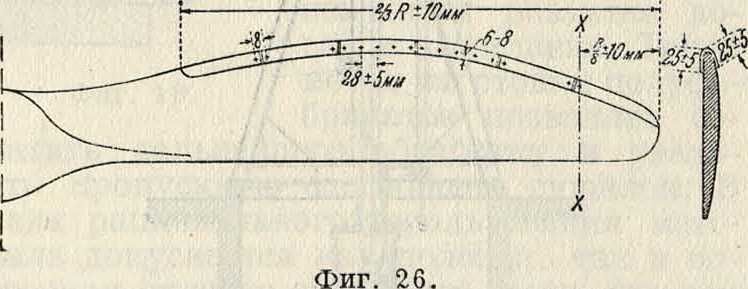
оковка лопастей латунью или дуралюминием толщиной 0,6 миллиметров для сухопутных самолетов и 0,75 миллиметров для гидросамолетов. Из ряда применяем, форм оковок (фигура 24—26) наилучшими являются оковки, позволяющие лопастям воздушного винта свободно сгибаться при работе (фигура 26). Для гидросамолетов применяется сплошная оковка концов лопастей. Оковка крепится или медными шурупами (фиг, 27) или сквозными медными или

дуралюминиевыми заклепками диам. 2,5— 3 миллиметров, причем головки запаиваются оловом. После опайки оковка зачищается напильниками и шлифуется наждаком. Во избежание вздутия оковки от попадания воздуха на концах лопастей в оковке просверливаются 3—4 отверстия диам. 2—3 миллиметров.

При производстве четырехлопастных В. в должна быть соблюдаема строгая перпендикулярность осей отдельных лопастей. Сложность производства, упаковки и транспортировки этих В. в привела к тому, что цщьные четырехлопастные винты в большинстве случаев заменяются двумя двухлопастными винтами, спаренными под прямым углом на одной общей втулке.

Характеристика завода массового производства В. в В основных своих элементах такой завод не имеет существенных отличий от правильно поставленного и оборудованного деревообделочного завода. Необходимы хорошо поставленное сушильное хозяйство для естественной и искусственной сушки и основные цеха: деревообделочный, столярный и лакировочный с добавлением специального цеха по оковке винтов. Специальное оборудование состоит: из копировальных станков, которые должны устанавливаться попарно, чтобы иметь возможность одновременной обработки рабочей

и нерабочей стороны лопасти В. в без смены шаблонов; сверлильных расточных—для рассверливания винтов под втулки; балансирных станков; прессов для склейки; специальных тумб для обработки винтов. Подсчет потребного оборудования и количества основных рабочих производится на основа нии след, норм обработки 1 В. в (в часах):

Ленточные пилы.. 1,5

Строгальные станки по дереву. 1,7

Фрезерные станки по дереву. 0,7

Циркулярные пилы .. 0,5

Сверлильные станки.. 0,85

Копировальные » 1,45

Шлифовальные » 0,5

Столярная обработка..26,75

Лакировочная отделка.. 7,2

В основание расчета сушилок и емкости лесных складов принимается средний расход лесного материала в 0,35 м³ на 1 воздушный ВИНТ. В. Малынич.

III. Металлические В. в Металлич. В. в за последнее время получили большое распространение вследствие лучшего их сопротивления атмосферным условиям и возм зж-ности в некоторых случаях их ремонта после механических повреждений.

Наиболее распространены следующие системы металлических В. в.: 1) Америк, винты Рида (фигура 28), изготовляются из одного куска литого дуралюмммя в виде плоской болванки, которой затем путем ковки, выкручивания и обработки придают фэрму двухлопастного винта. Ступицы этих винтов обычно похожи на ступицы деревянных винтов и бывают как деревянные, так и металлические. Эти винты широко распространены в америк. гражданской и военной авиации. 2) Винты Технич. отдела америк. воздушного флота (фигура 29), имеют съемные лопасти. Первые образцы этих винтов были изготовлены в 1922 году. Винт состоит из Стальной ступицы, сделанной из двух половин, образующих гнездо для разъемных лопастей. В каждую половину вставляется разъемная муфта, скреп-

ляющая обе половины и надеваемая на вал мотора. Каждому мотору соответствует только определенный просвет муфты, самая же ступица не меняется;поэтому, имея набор различных муфт, можно одним и тем же винтом пользоваться для самых разнообразных моторов. Особенностью конструкции этих винтов является использование зажимных колец ступицы для вертикального уравновешивания винта. Это достигается передвижением болта с ушками около ступицы по оси лопасти. Такая ступица, известная под названием расщепленной, заменила цельную в виду дешевизны, большей легкости сборки и уравновешивания винта. Эти винты введены на снабжение многих самолетов американок, сухопутной и морской авиации. Химич. состав материала этих винтов: меди 3—5%, магния 0,3—0,5%, алюминия 94— 95%; уд. вес 2,85; t° ковки, обработки и калки 460—475°. Механич. свойства: коэфф. крепости на растяжение 35—40 к г/мм“, предел упругости 20—30кг/лш², удлинение 15—20%, Нв_г 80—100. 3) Немецкие винты Хава (фигура 30), со съемными тонкими полыми дуралюминиевыми лопастями и стальной ступицей. Ступица имеет съемную коническ. насадку на носок мотора, пригоняемую по типу и мощности мотора, и составляется из

Фигура 30.

двух половин цилиндрич. трубы, в которую закладываются заплечиками концы лопас-тей, зажимаемые в ней хомутами на болтах. Закрепляющийся конец лопасти представляет собою стальную шайбу с заплечиками, от которой по длине лопасти идут два стальных стержня равного сопротивления. На эти стержни насаживаются для жесткости 5—6 нервюр, входящих составными частями в одну отливку с тыловой нерабочей стороной лопасти; толщина стенок 6—7 лш.По

Фигура 31.

рабочей стороне лопасти этот каркас покрывается листовым дуралюминием толщиной в ΐγ₂ миллиметров, приклепанным по кромкам и нервюрам дуралюминиевыми заклепками ^Английские винты Лейтнер а-У о т с а (фигура 31), изготовля ются не из алюминия, а из стали. Каждая лопасть делается полой, из листовой стали, причем необходимое уменьшение толщины достигается слоистой конструкцией, которая, к тому же, поглощает вибрацию.

Лопасти легко и точно регулируются и имеют большой диапазон шага. Их установка производится так же, как и в других системах со съемными лопастями.

Ступица представляет собою стальную, цилиндрическую трубу, состоящую из двух половин (фигура 32). Лопасти винта вставляются в ступицу и затягиваются болтами. Такие ступицы изготовляются для 2-, 3- и 4-лопастных винтов.

Лит.: Крейсон П.0 металлических винтах, «Вести, возд. флота», М., 1925, 12; его же, Металлич. винты, «Техника возд. флота», М., 1928, 5; «Aviation», N. Y., 1927, 30/V; «Flight», L., 1927, 42, 1926, 52; «Flugpost», В., 1926, 26, 1927, 22. П. Крейсон.