Волны

Волны, процесс распространения колебательного состояния в пространстве, на поверхности или по линии. На фигуре 1 показана мгновенная форма волны, для простейшего случая, при распространении вдоль прямой линии, причем по ординатам отложены значения рассматриваемого состояния. Волны могут возникать в любой среде, точки которой связаны между собою теми или иными силами взаимодействия. Распространение волны характеризуются в простейшем случае следующим синусоидальным или косинусоидальным уравнением:

у=A sin Ц (i — -^)=A sin 2π {- - -~_f) =

= A sin 2π — -0

Фигура 1.

или в комплексной форме:

. 2π i

Т I

у=Ае

M)

Физическ. природа у зависит от характера волнового процесса. Она может быть скалярного характера (уплотнение или разрежение в звуковой волне) или векторного характера (продольное или поперечное смещение точки, вектор электрической или магнитной силы и тому подобное.). А—амплитуда волны, t—время, протекшее от начала волнового процесса (которое можно выби-I рать произвольно), Т—период колебания,

Т. Э. m. IV.

х—расстояние рассматриваемой точки от центра возбуждения, υ—скорость распространения волнового процесса в единицу времени (ф а з о в а я с к о р о с т ь) и, наконец, λ=υ Т—расстояние между двумя точками, находящимися в одинаковой фазе, называемое д л и н о и В. Длина В. измеряется всегда в направлении распространения волн, то есть вдоль луча. Процесс, изображаемый приведенным выше уравнением, периодический как во времени, так и в пространстве. Если рассматривать определенную точку в пространстве (например х=х_г), то уравнение будет выражать простое гармоническое колебание, происходящее в этой точке; наоборот, при постоянном t уравнение принимает следующий вид:

х=A cos 2π (-γ +

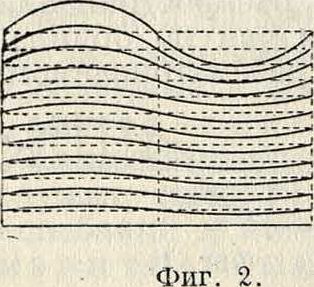
то есть изображает периодич. в пространстве форму В., где х стоит вместо t, а λ вместо Т т. о. длина В. λ является пространственным периодом формы В., подобно тому как Т— временным периодом колебательного движения. Приведенные данные относятся и к волнам, распространяющимся по линии; в более общем случае В. распространяются по многим направлениям. Геометрич. место точек, оказывающихся при этом в тождественной фазе, называется волновой поверхностью. Волна, исходящая из колеблющегося источника физически исчезающе малых размеров и распространяющаяся в однородной, изотропной среде, имеет шаровую форму; волны, исходящие от колеблющейся прямой, имеют цилиндрич. волновую поверхность, от колеблющейся плоскости—плоскую. Кроме вышеперечисленных пространственных В. в природе наблюдаются также и поверхностные В. (фигура 2— волновое движение вблизи поверхности жидкости), например круговые В., исходящие от камня, брошенного в воду. Поверхностные волны играют большую роль в процессе распространения электромагнитных волн вдоль поверхности земли. Если волновой процесс распространяется только вдоль одной линии, то поверхность В. сводится к точке.

Принцип суперпозиции (интерференция волн). Если в одном и том нее пространстве будут иметь место два или несколько волновых процессов, то значение волновой функции в зависимости от каждого процесса в отдельности выразится ф-лами:

Ух=A cos 2π (i - f); у,=A, cos 2π ( ^lf - -^rf- ),

где δ — разность хода, или разность фаз. Как показывает опыт, в большинстве случаев результирующая волновая функция будет геометрическ. (в частных случаях—скалярной) суммой отдельных волновых функций (принцип независимого наложения, или суперпозиции). Для электромагнитных В. принцип соблюдается точно; для упругих воли ои верен при достаточно малых амплитудах. В результате сложения двух или нескольких колебательных процессов в одной точке пространства может произойти интерференция. Необходимым условием интерференции является постоянство разности хода лучей. Важнейшим и простейшим случаем интерференции будет явление распространения двух тождественных волн в прямо противоположных направлениях. В этом случае для отдельных волновых функций получается:

Ух=А сов2л(ψ — у); у_г=А cos2ji ( у + у);

2r. t 2πχ

У=Ух + У 2=2A cos -у.- cos -у·

Это—ур-ие т. н. стоячей В. В то время как в поступательной плоской В. каждая точка вдоль луча имеет различную фазу, но одну и ту же амплитуду,—в аналогичной стоячей В. все точки вдоль луча будут иметь тождественную фазу, но различные амплитуды. Точки наибольшей амплитуды называются пучностями колебаний, а точки наименьшей или остающейся все время в покое амплитуды—у злами колебаний. В теории упругости доказывается, что в случае продольных стоячих В. узлы давления совпадают с пучностями колебаний, и наоборот. Так. обр. в пучностях колебаний будем иметь максимальную кинетическую и минимальную потенциальную энергию, в узлах наблюдается обратное явление.

Векторные В. разделяются на продольные и поперечные в зависимости от того, происходит ли распространение В. в направлении колебания или поперечно к нему. Примером В. последнего рода может служить обыкновен. колебание струны. В этом случае В. распространяется вдоль струны, в то время как колебания каждой материальной частицы совершаются перпендикулярно к струне. Примером продольных В. могут служить В. в газообразных и жидких телах, то есть звуковые В. В них частицы колеблются параллельно направлению распространения волн. В упругих средах могут распространяться как продольные (В. сгущения), так и поперечные. В. Упругое твердое тело может испытывать деформации двоякого рода: изменения объёма (вследствие уплотнения или разрежения) и изменения формы. Продольные В. возможны во всех средах, обладающих сжимаемостью, поперечные—только в средах, допускающих деформации сдвига и кручения.

Скорость распространения волнового процесса зависит от упругих свойств среды и характера движения. В ограниченной среде, папр. при распространении вдоль стержней, эта скорость будет зависеть также от геометрическ. размеров данного тела. Скорость распространения б. ч. не зависит от амплитуды колебаний (исключение—ные В. в воздухе), но скорость распространения световых В. в материальных средах и В. упругости зависит от частоты распространяющегося колебательного процесса. Для продольных В. теория дает следующую формулу скорости их распространения: v =, где E— мо-

дуль упругости, определяемый статич. опытами, а ρ—плотность вещества; аналогично для поперечных В. закручивания в стержнях поперечного круглого сечения имеем:

v= f/~у > ^где @—модуль сдвига, а ρ имеет указанное выше значение. Для поперечных В. изгиба получается более сложная зави симость: ν =

2π

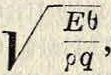
где Θ—момент инерции относительно нейтрального волокна, q— поперечное сечение стержня, а λ—длина волны; т. о. в В. этого рода скорость зависит и от длины В. (фигура 3— В. гиутия, распрост-Фигура з. раняющиеся по стер-

жню). Для скорости распространения продольных волн в газах

ф-ла V=у ~ принимает вид v=j ~, где

dp—приращение давления газа, а άρ—соответственное изменение плотности. В области звуковых В. мы имеем вследствие высокой частоты звуковых колебаний не изотермический, а адиабатический процесс, и в соответствии с этим Щ будет равно не —, как это имело бы место в изотермическом процессе, а —, где к есть отношение тепло емкости при постоянном давлении к теплоемкости при постоянном объёме: к — ^<:Р-‘ сле-

«в довательно, в газах» =

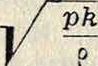
. Скорость зву ка в воздухе, в согласии с вышеприведенной теорией, равна 340 м/ск при нормальных условиях. В электромагнитных волнах скорость обусловлена соответственными электромагнитными константами и равна:

v_aM=Д, где с—универсальная постоян-V

пая скорости распространения электромагнитных В. любой длины в вакууме, равная приблизительно 3-10¹⁰ см/ск, ε—диэлектрич. постоянная, а μ—магнитная проницаемость среды. Эта формула неприменима в случае распространения световых и вообще диспергирующих электромагнитных В. в материальных средах, где скорость распространения зависит также и от периода колебаний. При переходе В. из одной среды в среду с другими физическими свойствами часть волновой энергии отражается, другая часть распространяется с изменившейся скоростью (отражение и преломление В.).

Поляризация В. Поляризованной В. называется векторная В., вектор колебания которой сохраняет неизменным свое направление; из этого следует, что поляризованы м. б. только поперечные В.

Энергетика волнового процесса. В плоской поступательной В., поскольку энеогия не абсорбируется средой, величина W потока энергии (то есть количества энергии, падающей в 1 ск. на 1 см^г поверхности, перпендикулярной к направлению распространения В.) остается постоянной;

в цилиндрической и поверхностной круговой В. величина W изменяется обратно пропорционально расстоянию, а в сферической—квадрату расстояния от центра возбуждения колебаний. Это станет очевидным, если принять во внимание, что полный поток энергии, остающийся неизменным, распространяется на все большие поверхности или линии. Следует помнить, что при волновом процессе не происходит переноса материи: каждая материальная частица совершает периодич. колебания вокруг своего положения равновесия, и ее средняя скорость за период равна нулю. В волновом процессе распространяется только энергия. Интенсивность музыкального тона, светового источника или электромагнитного излучателя пропорциональна, при данной частоте, амплитуде колебаний, следовательно на данном расстоянии амплитуда является мерилом интенсивности возбудителя колебаний.

Фазовая, сигнальная и групповая скорость. В новой физике понятие скорости распространения В. расчленяется на три различных, хотя и тесно связанных между собою, понятия, а именно различают фазовую скорость, скорость сигнала и групповую скорость. Если под фронтом В. понимать границу волнового процесса, то под скоростью сигнала надо понимать скорость распространения фронта В. Скорость распространения фронта электромагнитных В. любой длины (в том числе и световых и В., распространяющихся в материальных средах) будет всегда равна скорости с электромагнитных волн в пустоте (Зоммерфельд). Вследствие неодинаковой скорости распространения волн различной длины в материальных средах, форма сложной кривой, являющейся результатом сложения нескольких простых волн, будет меняться во времени и в пространстве. Скорость перемещения максимальн. амплитуды этой Фигура 5.

сложной кривой и будет называться групповой скоростью. Для простейшего случая групповой скорости двух волн, весьма мало различающихся по своей длине, Релей вывел следующую формулу:

Фигура 4.

ν_β=ν-λ

dip

где v—скорость простой, составляющей В., а λ—длина элементарной В. (фигура 4 и 5— группы волн).

Лит.: Хвольсон О. Д., Курс физики, т. 1, 2, 5, Берлин, 1923; Э и х е н в а л ь д А. А., Акустика и оптика, Москва, 1921; Столетов А., Введение в акустику и оптику, СПБ, 1902; Э д с е р Э., Общая физика, СПБ, 1913; Н о rt W., Techni-sche Schwingungslehre. Berlin, 1922; К о 1 a h n e A., Matliematische Akustik, Leipzig, 1910; Lamb H., Hydrodynamics, London, 1924. Ю. Барац.