 > Техника, страница 32 > Волны на поверхности жидкости
> Техника, страница 32 > Волны на поверхности жидкости
Волны на поверхности жидкости
Волны на поверхности жидкости. Под влиянием различных причин частицы поверхностного слоя жидкости могут прийти в колебательное движение. Такое движение охватывает все более и более далекие участки поверхности—по поверхности начинает распространяться В. Как и при возникновении других видов В., колебания могут происходить по закону синуса, по только при непременном условии, что амплитуда колебаний частицы мала по сравнению с длиной В. Длиной В. называется расстояние между двумя точками, где колебания оказываются в одной и той же фазе. Расстояние по вертикали от гребня до подошвы называется высотой В. Примером таких синусоидальных В. могут служить В. приливов: у них длина достигает сотен км, между тем как высота составляет обычно 7300 или даже 1/500 ее часть. В большинстве же случаев высотой волны нельзя пренебрегать по сравнению с ее длиной.
По сравнению с простыми поперечными колебаниями характер движения частиц жидкости всегда осложняется: они не просто поднимаются и опускаются по вертикальным направлениям, а описывают некоторые замкнутые орбиты, круговые или эллиптические. Первый тип орбит соответствует случаю, когда глубина очень велика по сравнению с длиной В., а второй—самому общему случаю, когда длина В. или больше расстояния до дна или, вообще говоря, соизмерима с ним. Можно показать, что при подобных вращательных движениях частиц профиль В. будет трохоидальным. Трохоида м. б. построена по точкам, если мы проследим, какой путь описывает точка, которая лежит на нек-ром расстоянии от центра круга, катящегося по прямой; в то же самое время точка, лежащая на самой окружности такого круга, опишет, очевидно, циклоиду.
На фигуре изображено возникновение тро-хоидального профиля при вращательных движениях частиц водной поверхности. Но

волновое движение не ограничивается одним только поверхностным слоем жидкости: волнение охватывает и лежащие ниже слои, только радиусы орбит частиц здесь непрерывно убывают с увеличением.глубины. Закон убывания радиусов таких окружностей
2 ttz
выражается формулой: г=а-е λ, где г — радиус орбиты частицы, лежащей на некоторой глубине г, а—радиус орбиты частицы, лежащей на самой поверхности (половина высоты В.), е—основание натуральной системы логарифмов, λ—длина В. Практически можно считать, что волнение прекращается на глубинах, бблыпих длины В. Скорость распространения волны ν выражается, в самом общем виде, ф-лой:
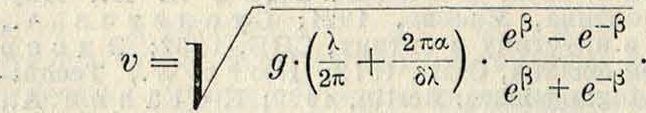
Здесь д—ускорение силы тяжести, δ—плотность жидкости, а—ее поверхностное натяжение; через β для краткости обозначено
2т: Н
отношение -., Н—глубина жидкого слоя (от поверхности до дна); остальные обозна чения те же, что указывались выше. Формула принимает более простой вид в трех частных случаях. ;
а) Приливные волны. Длина В. весьма велика по сравнению с глубиной Н. Здесь »=VдН, то есть скорость распространения зависит только от глубины, б) Глубина волны весьма велика по сравнению с ее длиной, но размеры В. все же настолько значительны, что капиллярными силами можно пренебречь. В этом случае оказывается, что
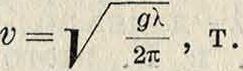
е. скорость распространения зависит лишь от длины В. Такая формула хорошо выражает скорость обычных морских В. в) Чрезвычайно короткие, т. н. капиллярные В. Здесь главную роль играют междуча-стичные силы, сила тяжести отступает на второй план. Скорость распространения ока зывается равной i/. Как видим, в
0 λ
противоположность случаю (б), здесь скорость оказывается тем большей, чем короче В.
Профиль В. очень сильно меняется под воздействием некоторых внешних факторов. Так, во время ветра передняя сторона В. делается значительно круче задней; при больших скоростях ветер может даже разрушать гребни волн, срывая их и образуя т. и. «барашки». При переходе В. с глубокого места на мелководье форма ее также изменяется; при этом энергия частиц толстого слоя воды передается слою меньшей толщины. Вот почему так опасен прибой около берегов, возле которых амплитуда колебаний частиц может значительно превысить их амплитуду в открытом море, где глубина водного слоя была велика.
Лит.: Шокальский Ю. М., Океанография, П., 1917; Lamb Н., Hydrodynamics, London, 1924; W i n с k e 1 m a η η M., Handbuch der Pliysik, В. 1, T. I, Berlin, 1908. В. Шулейкин.