> Техника, страница 33 > Всеобщая цепь электрического тока

Всеобщая цепь электрического тока

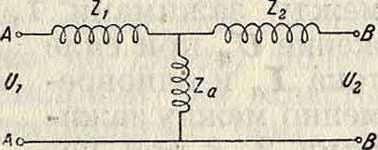
Всеобщая цепь электрического тока, эквивалентная схема, позволяющая рассчитывать сложные разветвленные электрические цепи, приводя их к более простому виду. Целый ряд электрических приборов и установок отличается тем, что у них имеются два зажима, к которым приключается первичное напряжение, и два других зажима, на которых возникает при этом свое, вторичное напряжение. Во многих случаях можно изучать работу этих фигура 1.

установок, не зная внутренних соединений, на основании общих свойств установок. Лакур показал [’], что во многих случаях эти цепи м. б. приведены к Т-образной схеме (фигура 1). Когда вторичные зажимы Б—В разомкнуты, то первичное напряжение холостого хода17₁₀на зажимах А—А пропорционально вторичному напряжению Г₂, ^τ· е. U_W=C₀U₂, где комплексный множитель С₀ определяется из постоянных цепи. Первичная сила тока ί₁₀ при этих условиях определяет полную проводимость холостого хода Υ₀=~, откуда I₁₀=C₀Y₀Uo. Если замкнуть вторичные зажимы В—В накоротко проводом, через который протекает ток 1₂, то Z7₃=0.

Тогда сила первич

ного тока короткого замыкания 1_1к==С_к 1₂, где постоянный множитель С_к тоже зависит от постоянных цепи. Первичное напряжение короткого замыкания V _1к определяет при этих условиях полное сопротивление короткого замы-

Фиг 2.

кания Z_k

и, к откуда U_lk=Z_kC_hI₂. Лакур

^Jk J V Ui — ^k^y

показал, что любое состояние нагрузки вторичных зажимов В—В может быть получено как результат наложения режима холостого хода при J₂=0 и режима короткого замыкания при Ϊ7₂=0. Это значит, что первичные сила тока и напряжение получаются как суммы

ТГг=Г₁₀ + Г_1к=С₀П₂ + Z_kC_kI₂

Iг=1го +Iik=Y*C_aU₂ + C_kI₂ j Нетрудно показать, что

Ц)

z,

C_er_eZ_e=l, г_к=г₁ + _ъ1 (l-Y₀Z_k)C_uC_k=l.

Определив постоянные при помощи измерений холостого хода и короткого замыкания, можно при помощи ф-лы (1) установить связь между первичными и вторичными ве-_г личинами при лю-

•-огштопплг-· бой нагрузке. От-

о_а и_е носительно развет-

--, вленной цепи необ-

Фигура з. ходимо предполо жить, что ее постоянные (сопротивление, индуктивность и т. д.) не изменяются. Такая схема может изображать не только неподвижные сети, но и цепи трансформаторов и даже двигателей, причем электрич. энергия, превращаемая в двигателе в механич. работу, изображается в виде энергии, теряемой в соответствующем омическом сопротивлении.

Воло [²] показал весьма удобный способ составления эквивалентных схем. Пусть имеется некоторая разветвленная цепь и четыре зажима 1, 2, 3, 4 (фигура 2), и пусть между зажимами J, 4 подводится напряжение U_а при силе „____„

тока 1_а и одновре- и_а gz₂ и_е

менно между зажи- --<---

мами 2, 3 при на фигуре 4.

пряжении Т7_е включается нагрузка, дающая силу тока 1_е. Тогда можно установить линейную зависимость

U_a=AU. + BI,

i_a=cu_e + Di_er

(3)

при чем обязательно

AD-BC =1. (3)

Вместо того чтобы полностью выписывать формулы (3), можно писать только опре-

А В

делитель (смотрите) из их коэффициентов

С Ό

Так,

например, для неразветвленной цепи с полным сопротивлением Z_x (фигура 3) мы имеем:

и_а=ТТ_е+ Ζ,Ι„ 1_а=1_е, (4)

так что определитель из коэффициентов равен 1 Ζ

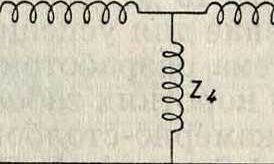
¹ Для линии с ответвлением (фигура 4)

О 1 мы имеем:

с определителем

ТТ=тт г

V а и _е, -i_a — _ζ

1 о

1

I. (5)

. Предположим теперь,

что мы включаем последовательно несколько цепей т. о., чтобы вторичные зажимы первого звена являлись первичными зажимами

I,

e-rum-

-лгшда-

Фигура 5.

второго звена и т. д. Так, например, если мы имеем две последовательно включенных цепи, то ур-ия (3) связывают начальные и конечные значения первой цепи. Для второй цепи будем иметь два аналогичных ур-ия: U_e=AU_e + BI

I» — CU + Dlf ⁽⁶⁾

Уравнения (3) и (6) дают возможность вычислить непосредственно

π^Α& + Β,ΤΑ

J«=C.U + DJJ’ ^<п

при чем коэфф-ты этой подстановки, как известно из теории определителей, вычисляются как элементы определителя, являющегося произведением определителей подстановок (3) и (6):

А В С D

А В’ ₌ АА’ + ВС ΑΒ +ΒΌ

СDj CA +DC CB +ΌΌ’

Так, например, можно вычислить сложную схему (фигура 5) как последовательное соединение схем, изображенных на фигуре 3 и 4.

-бГШТТПТШ⁴-

Z,

г“

nmr⁴-

Фигура 6.

Получаем для коэффициентов соответствующей подстановки элементы определителя, составленного как произведения четырех определителей:

1Z,		1 0	1Ζ3		1 0
0 1	X	έ*	xjo 1	X	k1

или г,и,+z,z,+z,z_t+z,z_t+z₉z,

ζ,ζ,+ζ,ζ,+ζ,ζ,

ZjZ,

z₉+z₉ + z₉

Ζ,

ζ,+ζ,

Z_tZi z_t

Увеличивая последовательно число включаемых элементов, можно, перемножая соответствующие определители, получить все более сложные коэффициенты, но во всех этих случаях между начальными и конечными величинами будет существовать линейная зависимость (3), причем коэффициенты будут связаны уравнением (3) (смотрите Фильтры электрические и Цепочечные проводники). Приведем еще коэффициенты двух более сложных схем, встречающихся на практике.

Для Т-образной схемы с шунтом (фигура 6) имеем коэффициенты:

— Z₉Z₉ Sjjj — Η,Ζ,Ζ,

ФИГ. 7.

S(i)~Z₁Z₉

где

S_(i)=^ Z ₂-l· Ζ ₃- -Z _i9

s,

(2) ^:

^iZa- -Z_lZ₃-)-ZiZ_i-[-Z.₁Z₃- -Z.iZ_t- -Z₃Z_t9

S(3)=Z₁Z._iZ₃- -Z₃Z₃Z ₃- - Z₃Z_iZ₁4-Z_iZ₁Z₂,

6=$£2) Z_XZ₃ Z₂Z₃.

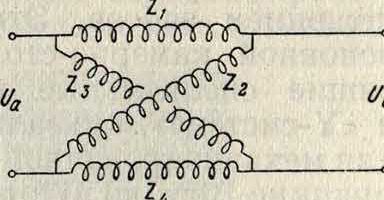
Для схемы с перекрестными соединениями (фигура 7) имеем коэффициенты:

ΖχΖ/2 ~ Ζ%Ζ	s(‘)
Р	P
S(.)	s^-ζ,ζ,-ζ,ζ.
P	P

где p=Z₂Z₃ — Z_xZ_t.

Закон составления коэффициентов показывает, что последовательность соединения отдельных элементов не безразлична и влия ет на. результат.

Лит.: ) La С о ur J. L., Leerlauf- und Tvurz-schluss-Versuch, Braunschweig, 1904; ²) V а и 1 о t M., Sur les constantes du quadripole passif, «RGB», Paris, 1927, t. 22, 13, p. 493; Френкель А., Теория переменных токов, пер. с немецкого, стр. 299, Москва— Ленинград, 1928. Я. Шпильрейн.