> Техника, страница 34 > Вычисления приближенные

Вычисления приближенные

Вычисления приближенные. Опытные данные дают всегда для измеряемой величины только приближенное значение (в пределах ошибки измерения); поэтому и все вычисления в прикладной математике имеют характер приближенный. Весьма важно уметь получить хорошее приближение наиболее коротким путем; правила для этого даются теорией приближенных вычислений.

Пусть величина А (к-рую будем считать положительной) приближенно измеряется числом а; если а<А, то а есть приближение по недостатку, если а>А, то—по избытку. Разность А — α= к называется истинной, абсолютной погрешностью приближения. Отсюда А=а±а. Обыкновенно а нам в точности не известно, но часто мы знаем, какое число а не может превосходить, например, при измерении длины к<0,01 см. Относительная погрешность е— отношение абсолютной погрешности а к приближенному значению а величины: е=“

(относительная погрешность часто дается в %). Так как результаты измерений обычно бывают выражены в десятичной системе, то практически абсолютная погрешность дает возможность судить, какие цифры являются «верными»; мы говорим, что число а есть приближенное значение с п верными знаками, если абсолютная погрешность не превосходит одной единицы последнего п-го разряда (считая только значащие цифры). Пусть

α= /с₀10^р-1 + 7г₁10*’-² +. + к_п__г 10*-", где 0 < к₀ < 10, 0 к_х < 10,., 0 е к„__г < 10; все п знаков верны, если а<10^р~^п. Иногда можно выбрать между приближенным значением по недостатку и избытку так, чтобы а <-| · 10^р~”; так, если нам известна (м+1)-я цифра к_п, то при определении п верных цифр с точностью до -J 10^р~^п следует оставить к_п_i без изменения, если к_п<Ь, и увеличить к_п__г на 1, если к_п 5 (правило дополнения). Выясним связь относительной погрешности ε с числом верных цифр и; если к < 10^р~^п, то

,. 10^р~“ ₌ i.

WO?-¹

во всяком случае, ε<-τ^; в случае применения правила дополнения, максимальная относительная погрешность вдвое меньше. Обратно: если для а максимальная относительная погрешность ε< то а содержит т верных цифр.

Пример. тг=3,14159.; значения с 4 верными знаками: по недостатку 3,141, по избытку 3,142, с абсолютной погрешностью <0,001; по правилу дополнения, 3,142 с абсолютной погрешностью < 0,0005; в последнем случае абсолютная погрешность

*<Шо<°>⁰²%·

Сложение. Из равенства А₁+А₂—а₁+а_г±а₁±и₂

следует, что абсолютная погрешность суммы ^ сумме абсолютных погрешностей слагаемых; если наибольшая абсолютная погрешность каждого слагаемого < и число слагаемых не больше 10, то абсолютная погрешность суммы < ₁₀,г i; чтобы получить в сумме т верных знаков, достаточно взять слагаемые с ш+1 верными знаками. Заметим еще, что относительная погрешность суммы не превышает наибольшей относительной погрешности слагаемых.

Вычитание. Абсолютная погрешность разности ^ сумме абсолютных погрешностей уменьшаемого и вычитаемого; но если разность мала, ее относительная погрешность может значительно превосходить погрешности данных чисел.

Умножение и деление. Пусть для чисел А и В имеем приближенные значения а и b; А=ᱫ, Β=ϋ±β. Абсолютная погрешность произведения АВ равна IАВ — аb=I bсс + αβ + «β · Относительная погрешность так как обыкновенно относительные погрешности малы, то последним слагаемым можно пренебречь и считать * =€ — + · то есть отно сительная погрешность произведения не м. б. заметно больше, чем сумма относительн. погрешностей множителей. В случае деления абсолютная погрешность частного -g- равна I А α I ± Ьа q: а? [.

117 Б i I вь I ’

относительная погрешность частного

± Ji ί о?. о__, b а _т β.

^S~ Bb ~Ь ~ ^± В а ^г В ’

так как b близко к В, опять имеем приближенно: «==— + ,. Т. о. после каждого умно-

а о жения и деления относительные погрешности складываются; если а и δ имели по п верных цифр, то и g<_1Cn-ii после умно-

.21

жения или деления получим; « <^n<]js=2·

Следовательно, чтобы получить в результате умножения или деления (или ряда этих действий, числом не более 10) т верных цифр, достаточно иметь данные числа с »t+2 верными цифрами. Эта оценка, однако, в большинстве случаев слишком груба; б. ч. мы получаем более точный результат.

Пример. Требуется вычислить яУ2, если множители даны с 4 верными знаками, и найти абсолютную погрешность произведения. Имеем: πei3,l42; 1,414 (по пра вилу дополнения). Произведение ^ 4,442788.

Относит, погрешность множимого < д₀- >

множителя < ; относительная погреш

ность произведения < ^ + 1Ш=tL· ^{; аб}‘ солютная ошибка произведения < 5 · =

= зЬо ^{< 0}>⁰⁰⁴ ‘ Следовательно, nV i ei 4,443 с ошибкой <0,05, то есть с 3 верными знаками. Мы видим, что последние 3 цифры произведения не играют в результате почти никакой роли, так как с избытком покрываются возможной абсолютной погрешностью; поэтому для экономии времени их не стоит вычислять. Существует такой прием упрощенного умножения приближенных чисел: оставляя в множимом и в множителе одинаковое число верных цифр, подписываем множитель под множимым в обратном порядке; затем умножаем множимое на цифры множителя, начиная слева, отбрасывая при этом во множимом те цифры, которые стоят правее цифры множителя, на которую производится умножение; результаты умножений подписываем так, чтобы правые цифры стояли в одном столбце, и складываем по столбцам. В нашем примере вычисления расположатся так:

3 142

4 141

3 142 1 256

31

__12

4 441

Таким образом опять получаем 3 верных цифры: лV~2=4,44.

Интерполяция. Задача интерполяции состоит в следующем: известны значения функции f{x) для значений аргумента х₀, x^Xg+h, χ₂=χ₀+21ι,.ι., и пусть f(x₀)=y₀, f{x_a+hi)=у_х, f(x₀+2h)=y₂,., где h—данное число; требуется вычислить (приближенно) значение fix) для промежуточных значений х. Простейший метод интерполяции есть линейная интерполяция. Мы допускаем, что в (малом) промежутке длины h изменение у пропорционально изменению х; пусть x₀+jch<x<x₀ + (Jc + l)h, тогда, по нашему допущению,

^v~^vk _ χ-(χι,+ftfr)

у“+1 -у к ^h

ИЛИ

у=Ук + Ьу_к·-~j~;

Ау_к — у_к+1 — у_к называется первой разностью функции Дж); если функция задана таблицей, то Ау_к есть табличная разность, и наша формула выражает правило пропорциональных частей. Если первые разности в таблице быстро изменяются, эта формула оказывается недостаточно точной, и надо прибегнуть ко вторым (и более высоким) разностям; 2-я разность

&Ук=ьук+ι - 4у к;

аналогично определяется 3-я разность, ит.д. Для интерполяции служит формула Ньютона:

Ау, Δ²3/.

У=Ук + -J- (Ж - (Ж - **) О - +

+ j—fci (ж - х_к) (Ж - ®Η·ι) (^ж - ^хк+2) + · · ·

Ограничимся вторыми разностями и преоб-

х—х,.

разуем формулу, полагая —j—=и, тогда

^х~^хк+1 ₌ fll* _ ^хк+х~^хк _{= и}_₁h h h

у=у_к +и-Ау_к + ^и(и^ А*у_к.

Пример. Требуется найти lgsin 0°1024". Находим из таблиц значение функции и вычисляем 1-е и 2-е разности.

X	lg Sin х	Ay	A-у
0°10 0°11 0°12	3746373 §750512 §754291	0,04139 0,03779	-0,00360

Имеем: χ — х_к=24"; h=V=60"; и=— =

= 0,4; и-1=-0,6.

Получаем:

lg sin ОНО=3,46373 и Ау=0,01656

Д²«=0,00043 _1-2 ^J__

lg sin 0°1024"=3,48072 Приближенное решение у p-и й. Дано ур-ие f(as)=0. Вычисляя значения fix) (например по таблицам), находим 2 таких значения х_г и ж₂, что 2/ι=/(®ι) и y₂=f(x₂) имеют разные знаки. Это значит, что кривая y=f(x) пересекает ось х между х_г и ж₂.

1-й способ. Чтобы приближенно найти точку пересечения, заменяем кривую прямой, соединяющей точки (x_lt у₂) и (ж₂, у₂), и ищем х₃—абсциссу ее точки пересечения с осью х (ордината у₃ =0). Имеем:

у»-ж. _ -Уi _>

Х_г-Ж, Уг-У, ’

ИЛИ

_χ=χ _

^{8 1}

Пример. Вычислить корень уравнения 3^!С=5а:, находящийся между 2 и 3. Предварительно логарифмируем ур-ие, получаем: zlg 3—lg х— lg 5=0. Вычисляем по таблицам у j (значение левой части при х=2) и у₂(значение при ж=3). Имеем: у_у=— 0,04576; у₂=+0,25527. Далее: ж_х=2; ж₂—£Ci=l и ?/₂—2/₁=0,30103; отсюда

_т _ О _ -0,04576 _ О 1 СО

" 0,30103 — *ЧО~.

2-й способ (способ Ньютона). В промежутке между и х ₂ заменяем кривую касательной в той из крайних точек, где

f ^{г г}

отношение -~>0. Абсцисса ж₄ точки пересечения этой касательной с осью х и дает приближенное значение корня. При этом геометрически ясно, что истинное значение корня лежит между значениями, получаемыми этим методом и предыдущим (смотрите фигура).

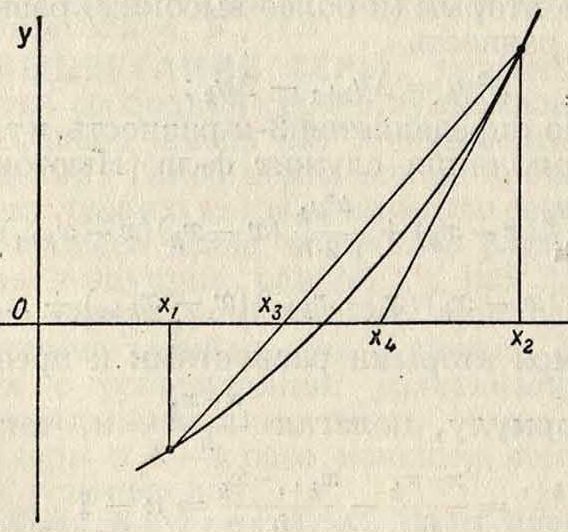
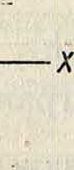
Приведем формулу для этого способа. Пусть точка х ₂ удовлетворяет вышеприведенному условию; обозначим значение производной в этой точке через у_г. Ур-ие касательной:

y-Vt=Vt(p—Xfd; при у=0, ж₄=ж₂ - ^ (для точки имели бы аналогично: x_t=x₁— jjj. Пример. Берем то же уравнение: у =×lg 3 - lg χ - lg S; у.=lg 3 - ^·

Неравенству -- > 0 удовлетворяет точка ж₂=3; у„=0,47712 - °’⁴|—=0,33236; х, =

= ³ - ^=³ - ISI=3-0,768=2,232. Итак,

истинное значение корня заключается между 2,15 и 2,23. Для лучшего приближения надо взять более близкие между собою значения ж₂ и х₂. Для приближенного решения алгебраическ. уравнений существует весьма удобный метод Греффе (смотрите Греффе метод).

Приближенное дифференцирование. По определению производной, f x)=

= lim^|; за приближенное значение мож-Ау но взять отношение теоретически это отношение тем ближе к производной, чем меньше Дж; но на практике, если функция задана таблицею, при малых разностях, относительная погрешность увеличивается (смотрите выше), так что невыгодно брать самые малые из возможных по таблице приращений.

d sin χ

Пример. Вычислить. при х=5°. Из таблиц имеем: у=0,00289; Дж=10=555755==Вычисляем с помощью логарифмов:

lg у=3,46090; lg Дж=lg л — lg 1 080 =

= 3,46373; lgЦ=1,99717; ^=0,9935.

Приближенное вычисление определенных интегралов. Т. к.

*1

jy dx измеряет площадь криволинейной тра-*0

пеции, то его приближенное значение получится, если мы заменим искомую площадь прямолинейной трапецией:

*1

jy dx ei h

x₀

Ур + Уг _ 2

Ji^ y^,f

Погрешность дается выражением —₂ - —^ (у "

есть значение 2-й производной от у в некоторой средней между ж₀ и ж₂ точке); она, вообще говоря, тем меньше, чем меньше й; поэтому,

ь если дан jydx, где интервал 6-а не очень а мал, вводим промежуточные точки деления: а=х₀, ж_1; ж_..ж_и=6 на равных расстоя ниях h=-^5; обозначая значение у при ж=ж_<через г/_г (г= 1, 2,., п), получаем формулу трапеций:

о, J

jydxoih < jy₀ + Vi + У-ι + · +Уп-1

l/.

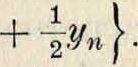
1 (Ь-α)³ у"

Погрешность дается выражением

(у"—значение 2-й производной в некоторой промежуточной точке) и, как видно, она приблизительно пропорциональна h²=^<b _rj-

Можно также разделить отрезок (а, b) на четное число п=2т равных частей и в каждом промежутке (ж₂,·, х₂(+₂) заменить кри-

вую параболой второго порядка, имеющей те же ординаты, что и кривая в точках х_2{> x₂i+i, площадь, которая ограни чена сверху дугой этой параболы, оказывается равной (y_2i + 4y_3i+1 + у_{м+ 2}). Для всего интервала (а, b) получим формулу Симпсона:

ь

dx οί о + 4«/j + 2у, +

а

4~ 4^3 4" · · · 4“ 2у_2т—₂ “Ь 4i/2m—X 4" У2т)· Погрешность при этом оказывается равной 1 (Ь-α)⁵ у"" п⁴ 5! ’ 4!

и, следовательно, при увеличении п убывает приблизительно пропорционально 4-й степени h.

г

Sdx

—. Берем

1

п=4; 7г =-= Уо — 1,0000; у_х — 0,8000; у₂ =

= 0,6667; у₃=0,5714, 2/₄=0,5000. Приближенное значение интеграла будет:

γ (Уо 4- 4у_г 4- 2 у_г 4- 4 у₃ 4- 2/₄) =

==0,6932;

таблицы дают: In 2=0,6931.

Дальнейшие методы приближенного интегрирования имеют своей целью дать возможность вычислять определенный интеграл, зная конечное число ординат, при помощи формулы вида:

А.=4- R-гУ-г 4“ · · · 4“ ИпУп где R_t суть одни и те же числа для любой функции у, зависящие только от числа п [чтобы устранить их зависимость от длины интервала, мы вводим новое переменное t формулой:

а+Ь, Ь-а,

^х=— + ~¹’

преобразующей любой интервал (а, b) в интервал (— 1, + 1)]. К этой группе формул относятся: ф-лаКотеса, ее частные случаи— формула трапеций и формула Симпсона, затем формула Чебышева:

+1

f f{x) dx=~ [f(x_x) + f(x₂) 4-. 4- Дx_n)

—1

где значения функции берутся в совершенно определенных точках.

При п=2

-х_г=4-ж₂=0,57735;

при п=3

= х₃=0,70711, х₂=0;

при п=4

-_Xl =_Xi=0,79465, -х_г=ж₃=0,18759; при п=5

—Χχ=х₅ — 0,83250, —ж₂=_Х) — 0,37454, ж₃=0 и т. д.

Сюда же относится формула Г а у-с а, которая дает даже точное значение интеграла, если f(x)—многочлен степени не выше 2и— 1; в этом случае: при п — 2

__Ж1=ж₂=0,57735, R₁=R₂=y_<при п=3

-_Xl=x₃ =, 0,77460, х₃=0, R_x=R₃ =

при η=4

— х_х — ж₄=0,86114, — х_г — х_а=0,39998,

R₁=R_i=0,17393, R₃=R₃=0,32607.

Приближенное вычисление неопределенных интегралов. Тре-

х буется найти значения F(X)=J*f(x)dx для

a

переменного X. Поскольку точное выражение F(X) неизвестно, мы должны построить таблицу значений этой функции или ее график. Здесь мы остановимся на 1-м способе (2-й способ — см. Графическое интегрирование). Применим формулу трапеций. Дадим×следующий ряд значений:

Χ₀=α; X_x—a- -h,.·, X_k=a+Jch,. Получаем:

a+kh

F(Xо)=0; F(X_k)=f f(x) dx ^

a

= h vo 4- У 4- ··· 4- y_k-1 + ~ζ Ук ] i

a+(k- -i)h

F(X_k+1)=f f{x)dx~

a

— h ^Уо 4" У 4- + Ук+ ч^а-н] j откуда

F(X_k+1)=F(X_k) 4- k{y_k 4- Ук+1)

Эта формула позволяет по значениям у₀, Vi> 2/2)··· последовательно вычислить Д-Xj), F(X₃) и т. д.

Приближенное интегрирование дифференциальных у p-и й. Дано дифференциальное уравнение=f x,y) требуется для разных значений х вычислить значение того решения дифференциального ур-ия у(х), к-рое при х=а принимает значение у=b. Задача сводится к тому, чтобы при заданном (малом) приращении к независимой переменной вычислить приращение к, которое получает у(х). Идея метода Рунге состоит в том, чтобы выразить это приращение к в виде суммы:

RJc 1 4“ R₃k₃ -J- R₃k₃ 4- jR₄/c₄,

где Ri—одни и те же для всех уравнений, а к_г представляют значения fix,у) для некоторых определенных значений аргументов, умноженные на приращение h. Рунге дал несколько схем для значений R и для вычисления к; особенно он рекомендует следующую:

к=-|/fCi 4- -j-&₂ 4- - к₃ 4- -jk_t,

где величины 7с_г последовательно вычисляются по формулам:

7с_х=f(a. b)-П; К=/(α + -|· & + |)·^

^з⁼⁼/(^а + ^> k_t f(a -·- 7t, 64- /r₃Wi.

Ф-ла оказывается точной для членов 5-го порядка относительно 7г. Исходя из полученных значений о₁=а+7г, 6j=b-(-/c, повторяем тот же процесс; получим таблицу для функции у(х).

Пример. ^=+++^; при ж—0, у=1. Требуется найти значение у при ж=0,2. Имеем: а=0; b=1; 7г=0,2; Λ®,»)=$=£· Вычисляем:

7с₁=Д0;1)-0,2=0,2;

7с₂=Д0,1; 1,1)=0,154;

Аз=Д0,1; 1,077)=0,152;

7с₄-- ДО,2; 1,152)=0,121;

7;=0,033+0,051+ 0,051+ 0,020=0,155.

Итак, при ж=0,2, у=1,155.

Существуют и другие методы интегрирования (например Штермера).

Лит.: Селиванов Д., Приближенные вычисления, Л., 1922; Крылов А. Н., О приближенных вычислениях, СПБ, 19И; Б е з и к о в и ч Я. и Фридман А., Приближенные вычисления, Ленинград, 1926; Крылов А. Н., Приближенное численное решение обыкновенных дифференциальных уравнений, Берлин, 1923; Eunge С. und К б и i g Н., Vorlesungen Uber numersches Recli-nen, Berlin, 1924. В. Степанов.