> Техника, страница 34 > Гаечный ключ

Гаечный ключ

Гаечный ключ, инструмент, служащий для отвинчивания и завинчивания гаек. Усилие Q, необходимое для завинчивания или отвинчивания гайки, приведенное к радиусу внешней окружности резьбы, выражается следующим образом:

п ₌ plf О, + eosMgq

Τ ^ V ¹ <2 ¹ COS β—/-tga/’

где Р—нагрузка в килограммах на болт вдоль его оси, а—угол наклона средней винтовой линии резьбы к опорному торцу гайки, Ζβ—угол при вершине треугольника, образующего остроугольный профиль нарезки, f—коэфф. трения между поверх ностями резьбы у бол та и гайки, Д—коэфф трения между гайкой i

Фигура i.

Фигура 2.

опорной поверхностью, D—наружный диаметр в сантиметров кольцев. площади торцевой опорной поверхности гайки, d—внутренний диаметр в ем той же поверхности, равный наружному диаметру болта. Момент, вызывающий изгиб в челюстях и рукоят- |

ке ключа при его работе, М_ь= Q— тем.

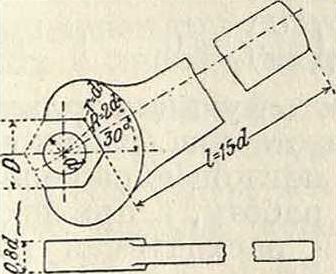
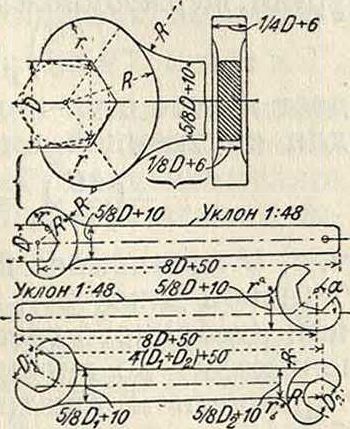
Прочные размеры для Г. к. определяются расчетом на изгиб челюсти и рукоятки. Пра-вильн. форма и размеры Г. к., по Баху, указаны на фигуре 1. Построение очертания челюстей и размеры американских гаечных ключей изображены на фигуре 2. Размер че-люстей в направлении, перпендикуляры, к оси

-ΕΞΞΞ34-4·

гайки в плоскости ее грани, выполняется или

) (

Фигура 3.

Фигура 4.

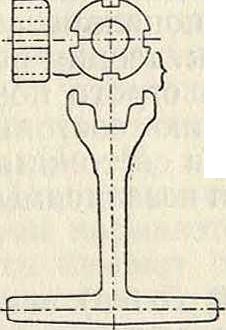
равным d или более d на 3—5 миллиметров. Изготовляют обычно Г. к. из литого железа штамповкой. Г. к. из ковкого чугуна дешевле, но не так прочны, как штампованные. Поперечному сечению рукоятки гаечн. ключа часто придают двутавровую форму. Для гаек утопленных или расположенных так, что работать нормальным ключом не представляется возможным, употребляются торцевые ключи (фигура 3); для круглых гаек, имеющих на боках высверленные углубления или пропиленные пазы, применяется бель-

Фигура 5.

Фигура 6-

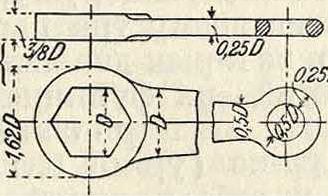
гийский ключ (фигура 4); для круглых утопленных гаек применяется вильчатый ключ (фигура 5). В тех случаях, когда желательно уменьшить толщину челюстей, Г. к. выполняют с замкнутым зевом (фигура 6). Для того, чтобы можно было одним ключом завинчивать гайки различных размеров, Г. к. выполняют с раздвижными щеками; такие Г’, к.

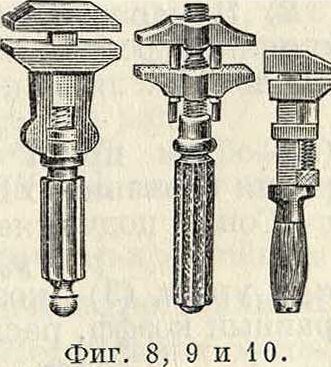
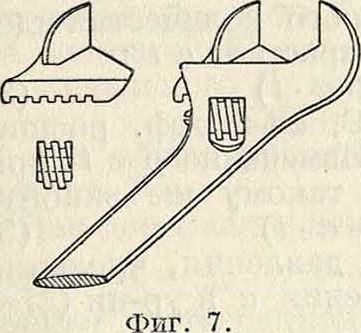
называются универсальными. Из многочисленных конструкций универсальных ключей наиболее совершенной является конструкция шведского ключа Бако (Вайсо, фигура 7); менее удобны для работы ключи— английский (фигура 8), французский (фигура 9) и швейцарский (фигура 10).

Лит.: Сидоров А. И., Курс деталей машин, 2 изд., ч. I, М.—Л., 1927; е г о же, Детали машин. Таблицы чертежей, М., 1925. Б. Шпри ни.

Г АЗ. Газообразным состоянием называется такое состояние вещества, в к-ром силы, действующие между молекулами, чрезвычайно малы и размеры самих молекул ничтожны сравнительно с промежутками между ними. Между столкновениями молекулы Г. двигаются прямолинейно, равномерно и совершенно беспорядочно. При нагревании и разрежении все Г. стремятся к предельному состоянию так называемого идеального, или совершенного Г.

В идеальном Г. междумолокулярные силы равны нулю, и объём самих молекул бесконечно мал сравнительно с объёмом меж-думолекулярного пространства. Состояние идеального газа является тем предельным разведенным состоянием вещества, к которому стремятся все тела природы при достаточно высоких t° и достаточно низких давлениях; в этом и заключается особое значение состояния идеального газа, к тому же наиболее просто поддающегося исследованию и потому полнее всего изученного. Вещество, в крайнем разрежении заполняющее межпланетное пространство, может считаться находящимся в состоянии идеального газа.

Газовое давление р обусловливается ударами молекул Г. о стенки сосуда. Согласно кинетической теории (смотрите), средняя кинетич. энергия молекул Г. пропорциональна абсолютной темп-ре. В кинетическ. теории показывается, что идеальный газ строго подчиняется следующему уравнению состояния, связывающему три параметра состояния: v, 7и р, из которых два являются независимыми, а третий—их функцией:

р · v=В Т. (1)

Это ур-ие (ур-ие Клапейрона) заключает в себе в явной форме три основных закона состояния идеального Г.:

1) Закон Бойля-Мариотта. При постоянной Т произведение р-v для данного количёства идеального газа есть величина постоянная (p-v=Const), то есть объём идеального газа v обратно пропорционален его давлению р:изотермы идеального газа в системе координат (v, р) являются равнобокими гиперболами, асимптотами которых служат оси координат.

2) Закон Гей-Люссака. При постоянном р объём данного количества идеального Г. линейно возрастает с t°:

v=v₀(l +a-t) (2)

(v₀—объём при i°=0°C, а—коэфф. расширения идеального Г.). Изменение pci³ при v=Const подчиняется такому же закону:

jp=Po(1 + “ · 0· (3)

а в ур-ии (3)—коэфф. давления, численно равный коэфф. расширения а в ур-ии (2)== ^Т= 0,00367—величина, не зависящая от природы Г. и одинаковая для всех идеальных Г.; р₀—давление при t°=0°С. Вводя вместо t абсолютную темп-ру

T=t+ ~ =t + 273,1,

а находим вместо уравнений (2) и (3):

ν ₌ _А»_. Т:

273,1 ’

(4)

Р =

Уо _щ ηι 273,1

(5)

3) Закон А в о г а д р о. Из ур-ия (1) видно, что газовая постоянная

В=γ·ν₀ пропорциональна нормальному объёму ν₀, занимаемому данным количеством Г. при нормальных условиях (р₀=1 Atm и ί₀=(ГС=273,1° К), то есть обратно пропорциональна плотности газа при нормальных условиях D₀. По закону Авогадро, при одинаковых р л Т все идеальные газы содержат в равных объёмах (например, равных v₀) равное число молекул. Обратно: равное число молекул (например, 1 моль=1 граммо-лекуле) всякого газа в идеальном состоянии занимает один и тот же объём v₀ при нормальных условиях, независимо от природы Г. (в 1 моле всякого вещества содержится 7 г„=6,06 · 10²³ отдельных молекул—ч и с л о Авогадро). Найдено с большой точностью, что нормальный молярный объём любого идеального газа {У₀)_м ра вен 22,412. Отсюда можно рассчитать

МОЛЬ

число молекул в 1 см³ любого идеального Г.

6,06- ю^г!

при нормальных условиях: щ=—, ₂₂ =

= 2,705·10¹⁹ см³ (число Лошмита). При помощи ур-ия (1) закон Авогадро выражается в том, что газовая постоянная В при расчете на 1 моль любого Г. будет одна и та же, независимо от природы Г. Т. о. R является универсальной постоянной с раз-мерностью “ выражает работу расширения 1 моля идеального Г. при нагревании его на 1°С при р=Const:

Из этом и состоит физическое значение В.

(6)

В =

273,1

υ_α

находим числовое значение

В =

1 · 22,416

273,1

В других единицах моль) таковы:

0,082

литр атмосфер моль град, значения В

(на 1

Л=8,315-10⁷-

эрг

= 1,987 -

cal,

моль град. - _мопь град.

Кроме разобранных трех законов, из уравнения (1) состояния идеального Г. в соединении с двумя началами термодинамики следуют еще такие основные законы:

4) 3 а к о н Джоуля. Одно из общих ур-ий термодинамики (смотрите)

-(т _

За )χ

С)

дает вместе с ур-ием (1) следующие условия для внутренней энергии U идеального Г.:

-(Г).-»»®,-»· ⁽⁸⁾

т. e. U идеального газа есть функция только Г (закон Джоуля); при изотермич. расширении идеального газа все поглощаемое тепло переходит во внешнюю работу, а при изотермическом сжатии вся расходуемая работ—в выделяющееся тепло.

5) Теплоемкости идеального Г. при постоянном объёме с„ и при постоянном давлении с„ являются функциями одной лишь Т (смотрите Теплоемкость). Термодинамика дает общие уравнения:

)

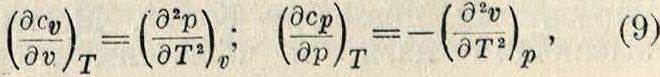
но для идеального Г. р и v линейно зависят от Т, по закону Гей-Люссака (4) и (5); следовательно, правые части уравнений (9) обращаются в 0 и

Теплоемкости с_р и с„ не независимы друг от друга, но связаны для идеального Г. простым условием:

Ср — Су — R

(10)

вытекающим из газовых законов (R имеет размерность теплоемкости), то есть, если с„ и

Су относить к 1 молю идеального Г., то они разнятся между собой на 2 (точнее—на 1,986) ——ί--

⁷ моль град.

В кинетической теории принимается, по принципу равномерн. распределения энергии, что на каждую степень свободы газовой молекулы приходится энергия £ к„Т, а на 1 моль приходится

№„= -

н

~ Л₀ · Т- N₀=~R есть газовая

v₀= — тг curb laauHcUl ПОСТОЯННая, раССЧИ-

тайная на 1 молекулу — постоянная Больцмана). Числом степеней свободы (г) называется число независимых друг от друга видов механич. энергии, которой обладает молекула Г. Тогда энергия 1 моля

U=^:r.T и с.=(|5)=1ч-Л. (11)

c_v=c_v + R={^i+l) -R (12)

(приближенно, считая R=Z, c_v=i, c_p=i+2). В учении о Г. важную роль играет отно ¹³

шение -^р-=у; из уравнений (11) и (12):

^CV

о

У =1+7-··

(13)

В простейшем случае одноатомного Г. (молекула которого состоит из 1 атома, каковы благородные Г. и пары многих металлов) г наименьшее и равняется 3: вся энергия молекулы сводится к кинетич. энергии ее поступательных движений, которые могут совершаться по трем независимым взаимно перпендикулярным направлениям; тогда

Су=2,98^3—°⁵¹-,с„=4,98^5——,

^г ’ моль град. Р ’ моль град,

а у имеет наибольшую возможную величину:

у=-у=1,667. Для двухатомных Г.

(Н₂, 0₂, N_2i СО и другие) можно считать 1=3 + 2 (два вращения вокруг двух взаимно перпендикулярных осей, перпендикулярных к линии, соединяющей оба атома); тогда с„=4,96 ^5, с_р=6,95 7 и у=-1 =

= 1,40. Для трехатомного Г. (Н₂0, С0₂, ITS, N₂0) 1=3 + 3 (вращение вокруг трех взаимно перпендикулярных осей) и

c„=5,96ei6, Ср=7,95^8 и у=-|-=1,33.

При дальнейшем усложнении строения молекулы, то есть с увеличением 1, возрастают с„иСр, а у=1 + -J- и стремится к 1. Таблица 1

показывает, что все сказанное хорошо согласуется с данными опыта, что у всегда >1 и sS 1,667 и не может быть=1,50 (для 1=4).

Таблица 1.—Экспериментальные значения c_tt, Ср и i для газов.

	Число вые значе ния г	Газы	Сред пр Су	ние зна И t°£l 2 Ср	чения )°С Т
	3	Hg (пары). Не, Аг
		И др.	2,9	4,9	1,66
	5	Воздух, Н2, Ns, Os,
		со	4,91	6, 90	1,404
	6	ИаО (пары), ΟΟ,ΝίΟ,
		HaS	6,1—7,3	8,3—9,2	1,31
	—	Пары эфира (слош-
		ные многоатомн.
		молекулы)	32	—	1,06

Для одноатомных Г. и в соответствии с теорией, практически не изменяются с Т (так, для Аг значения с„ и с_р лежат в пределах от 2,98 до 3,00 между 1°=0° и 1 000° С). Изменения с_аи с_р с t° находят объяснение в теории квант. Впрочем, теплоемкости Г., близких к идеальным, практически почти не изменяются в широких интервалах температуры. Экспериментально определяются обычно Ср и у, а с„ вычисляется из этих данных.

Реальные Г. Все Г., существующие в действительности,—реальные Г. б. или м. уклоняются от законов идеальны хГ., но тем меньше, чем выше 1° и чем ниже р. Т. о. законы идеальных газов являются для реальных газов предельными. При обычной 1° уклонения меньше всего у Г., t°_Kpum_ которых чрезвычайно низки (т. и. постоянные газы: Не, Н₂, N_s, 0₂, воздух); у газов же со сравнительно высокой t°_KVUm- и у паров (паром называется Г. при t°< t°_KVUm.) уклонения бывают очень значительны. Причины уклонений реальных Г. от газовых законов заключаются в том, что: 1) в них действуют междумолекулярные силы; поэтому поверхности, молекулы втягиваются внутрь газов силами, равнодействующая которых, рассчитанная на единицу поверхности и направленная перпендикулярно к ней, называется молекулярным (внутренним) давлением К; 2) не весь объём Г. v, а только часть его (v—b) дает свободу для движений молекул; часть объёма b, коволюм, как бы занята самими молекулами. Если бы газ был идеальным, его давление было бы больше наблюдаемого р на величину К; поэтому уравнение состояния реального Г. напишется в виде

(p+K)-(v—b)=R Т. (14)

В этом общем уравнении К и b могут зависеть от Т и v.

Ван-дер-Ваальс показал,что в простейшем случае К=^, а b—величина постоянная, равная учетверенному объёму самих молекул Г. Таким образом уравнение Ван-дер-Ваальса имеет вид:

(р+£) ·(»-&)= 5ΜΪ; (15)

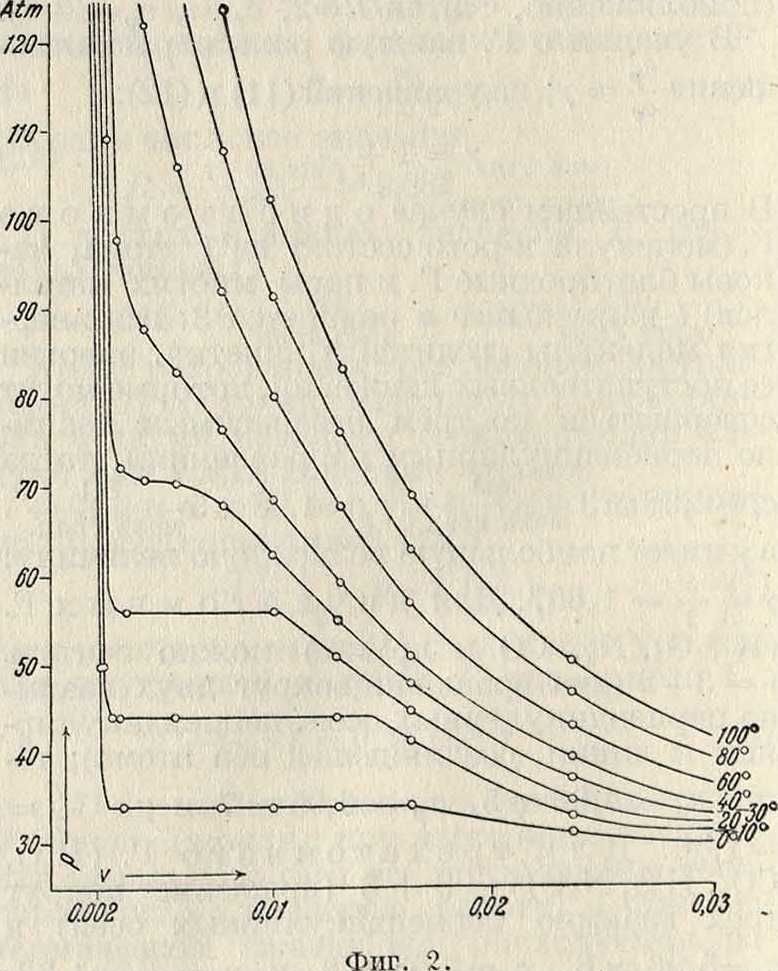
а и b, константы Ван-дер-Ваальса, как показывает опыт, все же зависят от Т иг», и потому ур-ие (15) является лишь первым приближением; оно хорошо передает качественную форму изотерм реальных Г. Иа фигура 1 изображены для С0₂ теоретич. изотермы: S-образные части этих изотерм отвечают термодинамически мета-стабильным состояниям. На фигуре 2 изображены для С0₂ экспериментальные

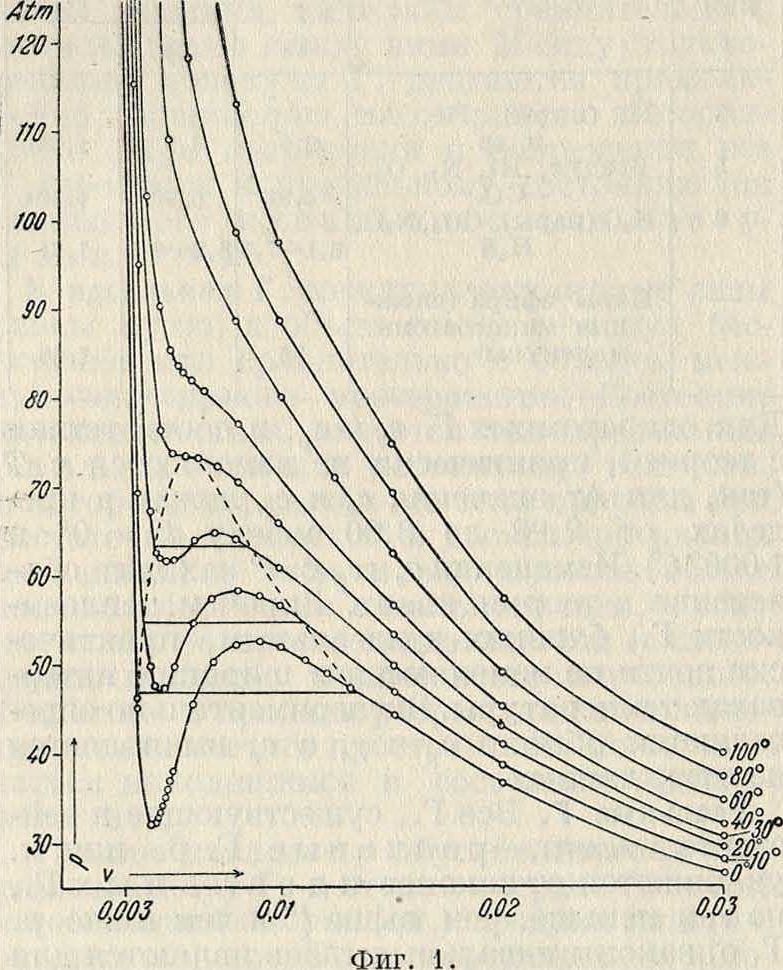
изотермы: S-образные части кривых заменены прямолинейными частями; справа от этих частей кривые соответствуют газу (ненасыщенному пару), слева — жидкости, а сами прямолинейные отрезки—равновесию пара и жидкости. Ур-ие (15), в полном согласии с опытом, показывает, что с повышением t° размеры прямолинейных отрезков на изотермах делаются все меньше (фигура 2) и, наконец, при некоторой t°=t°_Kpum. длина этого отрезка обращается в 0. При t^a>t°_Kpum. Г. не может обращаться в жидкость ни при каких давлениях: жидкость перестает существовать. Т. о. уравнение Ван-дер-Ваальса охватывает два состояния—газообразное и жидкое—и служит основанием для учения о непрерывности перехода между этими двумя состояниями. Критические темп-ры для некоторых Г. имеют следующие значения: + 360°С для Н₂0, +31°С для С0₂,-241°С для Н₂ и — 254°С для Не.

Ожижение Г. Всякий Г. можно обратить в жидкость надлежащим давлением, предварительно охладив его ниже t°_VVUm.· Необходимые для ожижения С0₂ давления (в Atm) при разных t° приведены в таблице 2.

Таблица 2.— Давления р₃, необходимые для ожижения СО_г при разных i°.

ί°	PsAtm		PsAtm
+31	77 (=Pupum.)	-54	5,5
-34	12,7	-64	3,1
-44	8,7	-80	1,0

Понятно, что эти давления являются давлениями насыщенного пара жидкой углекислоты и тем ниже, чем низке температура.

Чтобы предварительно сильно охладить Г. для ожижения, в технич. установках пользуются эффектом Джоуля-Том с о и а, заключающимся в том, что при адиабатическом расширении (иапр., при резком падении давления, когда Г. вытекает из отверстия) внутренняя энергия Г. возрастает на ΔΖ7, а Т изменяется на Δ7⁷, причем термодинамически

*^τ=[^τ(.Ά-^νΥί· ⁽¹⁶⁾

В случае идеальных Г. Δί7=0 и 1Т=0 [так как, по ур-ию (1), Т~--ν=oj.

Для реальных Г. Δ7¹ > 0, то есть происходит охлаждение или нагревание, смотря по тому, будет ли Т-^ - ν < 0 (Δρ < 0). По урав-нению Ваи-дер-Ваальса,

гт1 &V Ч j

¹ дТ ~^υ — дТт ^{— &}

(с достаточным приближением). Т. о. при достаточно высоких температурах все Г. при адиабатич. расширении нагреваются (ΔΓ>0,

т. к. < δ), но с понижением температуры для каждого газа наступает инверсионная точка T_it определяемая условием δ=0, ниже которой газы начинают охлаждаться при адиабатическом расширении при Т< T,j. Для всех газов, кроме Н₂ и Не, 1 лежит выше обычных t° (так, для воздуха 7) соответствует +360°С), и потому Г. могут быть озкижены

по принципу Линде, без предварительного охлаждения. Для Н₂ инверсионная точка 2 —80,5°С, а для Не—далее 15°К; •поэтому Н₂ и Не для ожижения должен быть предварительно охлаждены ниже этих t°.

Соответственные состояния. Критические температура Т_к, давление р_к и объём ν_κ μ. б. выражены через константы Ван-дер-Ваальса а, b и R след, образом:

т 8 a-b 1 a ni /irN

^Тк~ 27 ~ВГ’Р^{К =} 27 ‘ ^ ^{; Vk=35}· (¹⁷)

Если за единицы измер. Т, р и v принять соответственно критич. величины, то вместо Т, р и v состояние будет характеризоваться приведенными величинами:

(18)

Если ввести θ, п и φ в ур-ие Ван-дер-Ва-альса (15), то константы а, Ь и R сократятся, и получится приведенное у p-и е состояния, с численными коэфф-тами

(я+-^)-(Зу-1)=8в, (19)

вовсе не содержащее величин, зависящих от природы вещества. Ур-ие (19) предполагает, однако, правильность ур-ия Ван-дер-Ваальса, и потому уклонения от него часто весьма значительны, особенно в случае ассоциированных веществ. Учение о соответственных состояниях (так называются состояния, отвечающие одинаковым Θ, к и φ) дает возможность находить большое число универсальных зависимостей, подобных уравнению (19).

Применение Г. Сжатые и ожиженные Г. применяются в технике всюду, где нужны значительные количества газа в небольшом объёме; так, С0₂ применяется для газирования вод, С1₂ и —в военнохимическом деле, 0₂—для медицинских целей, сжатый воздух—для пуска двигателей внутреннего сгорания. Особенное значение ожиженные Г. (С0₂ и ΝΗ₃) имеют в холодильном деле, в холодильных машинах (например, для получения искусственного льда). Легкие Г. (Н, светильный газ, в последнее время Не) применяются для наполнения аэростатов. Инертные Г. (Ν₂ и благородные Г., особенно Аг) применяются для наполнения полуваттных ламп накаливания. Особняком стоит применение газа для освещения или в качестве топлива: светильный, силовой, водяной газы и другие (смотрите Газовое производство).

Лит.: Бирон Е. В., Учение о газах и жидкостях, М.—П., 1923; Хвольсоп О. Д., Курс физики, т. 1, 3, Берлин, 1923; Бачинский А., Введение в кинетич. теорию газов, М., 1908; Тим и-р я з е в А. К., Кинетич. теория материн, М.—П., 1923; Van derWaals J. D., Ober die Konti-nuitat d. gasformigen und llussigen Zustandes, Lpz., 1899—1900. П. Ребиндер.