Гамма-функция

Гамма-функция, эйлеров интеграл второго рода, для положител ь-ного числа р определяется формулой со

Г(р)=J х?-¹е~^х dx.

Непосредственно имеем: г(1)=1 интегрирование по частям дает: г (р)=(р— 1 )Г(р— 1). Эти две ф-лы являются основными для Г.-ф. В частности, при п целом, имеем:

Г(и)=(и— 1)Г(и—1) =.

.=(«—1)(ю—2).2-1-Г(1)=(м—1)!

Если р — п+к, где п—натуральное число,

0<α< 1, то имеем:

Г(»г+а)=(и—1+а)(я—2-Fa). (1+«)·« Г(а).

Т. о. достаточно в таблицах дать значения Г.-ф. для значений аргумента между 0 и 1; все остальные значения легко вычислить по последней ф-ле. Отметим еще соотношение:

Г(р) Г(1 _«)= —;

эта формула позволяет вычислять значения Г для 7г <р <1. если известны значения Г.-ф. для аргументов между 0 и у_г. В частности, из этой формулы следует:

оо СО

Г (-М=J x~*e~^xdx — 2 j c~^z‘ dz=Vn;

ο υ

оо

J e~^ldz называется интегралом П у а с-

ОН

со н а. Для больших значений п имеем приближенное выражение гамма-функции: Г(П+1)=п ^ n^le~"VZnn (формула Стирлинга). Эйлер дал также выражение гамма-функции в виде бесконечного произведения:

1(ж) =

я(а;-И). (х+П - 1)

Это выражение позволяет определить Г.-ф. также для отрицательных и комплексных значений ж; она оказывается непрерывной в виде многоэтажных зданий. Выбор между системами одноэтажной и многоэтажной определяется исключительно стоимостью земельных участков, и потому в больших городах Запади. Европы и особенно Америки начинают отдавать преимущество многоэтажным Г.; так, в С. Ш. А. уже существуют Г. в 44 этажа, емкостью в 3 000 автомобилей.

На фигуре 1 представлен разрез большого одноэтажного Г. на 200 автобусов. Уровень пола в таких Г. располагается по возможности на уровне дороги, для облегчения

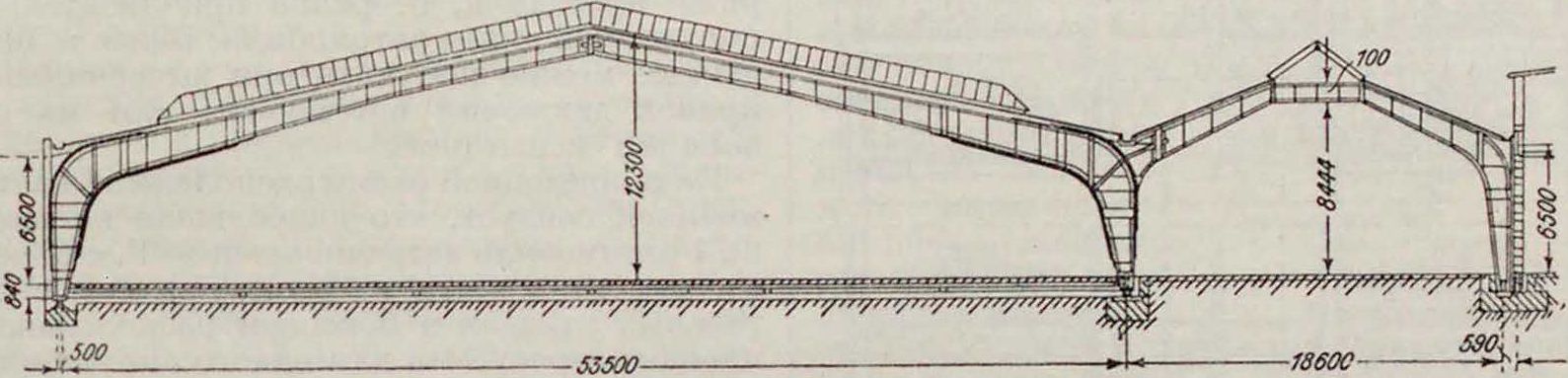
Фигура 1.

всюду, кроме значений х= 0,-1,—2,., где имеет полюсы 1-го порядка. С Г.-ф. связана еще функция:

Н(р.?) — ^ ж)^9-1 dx (р>0, q> 0)

(бета-функция, или эйлеров интеграл 1 рода). Ее выражение через Г.-ф.:

^{Р 4} I (j>+q)

го

Лит.: Ч е з а р о Э. Элементарный учебник ал-геОраическ. анализа, ч. II. пер. с нем. Одесса, 1914; Л ахти н Л. К., Кривые распределения и построение для них интерполяционных формул но способам Пирсона п Брунса, М. 1922. В. Степанов.