> Техника, страница 35 > Гармонический анализ

Гармонический анализ

Гармонический анализ, разложение сложных периодич. кривых па простые гармонические. Согласно теореме Фурье (смотрите Фурье теорема), всякую сложную периодическую функцию с периодом Т можно разложить на конечное или бесконечно большое число простых периодических функций с периодами T. V* Т, ¹/₃ Т, % Т и т. д. Эти простые периодические функции являются синусоидальными функциями и называются простыми гармоническими. Простым преоб разованием период Т можно привести к 2л; тогда можем представить теорему Фурье в следующем виде:

/(0⁼, Aq -j- yl| cos t -J- .4 £ cos -p.-)-Zi₁.si ni -f-

+ ii.,sin2i+.= ’ A₀+ 2(.^„ccsni-f _B_nsinw<)·

Коэфф-ты А и В представляются в виде

2" 2п

-4„= ^sinntdf(t), В_п= _t_r ^ cos ntdfit).

о о

Эти коэфф-ты называются амплитуд а-м и соответствующих простых гармопическ. функций. В задачи Г. а. данной сложной периодической функции входит определение амплитуд и фаз простых гармонии. функций, составляющих данную сложную функцию, или, выражаясь аналитически, определение коэффициентов, дающих возможность представить данную сложную периодич. функцию в виде ряда Фурье. Г. а. заключается, поэтому, в определении вышеуказанных двух интегралов. Математическ. приборы, при помощи которых производится Г. а., являются т. о. интеграторами (смотрите), определяющими интегралы указанной формы. Г. а. необходим для чрезвычайно большого числа практических исследований в технике и вообще в науке. Все периодич. двиясения, все колебательные и вибрационные явления (смотрите Вибрацгт) требуют для своего изучения Г. а. Огромное количество явлений физических (акустических, электрических и др.), механических, метеорологических (определение периодичности изменения t° и давления воздуха) и даже физиологических (биение сердца и тому подобное.) может быть полностью уяснено только при помощи Г. а.

Существует целый ряд математич. приборов, т. н. гармонических анализаторов. Из них наиболее распространенным является анализатор Генричи-Коради (Неп-rici-Coradi). Рамка ЕЕ (фигура 1), покоящаяся

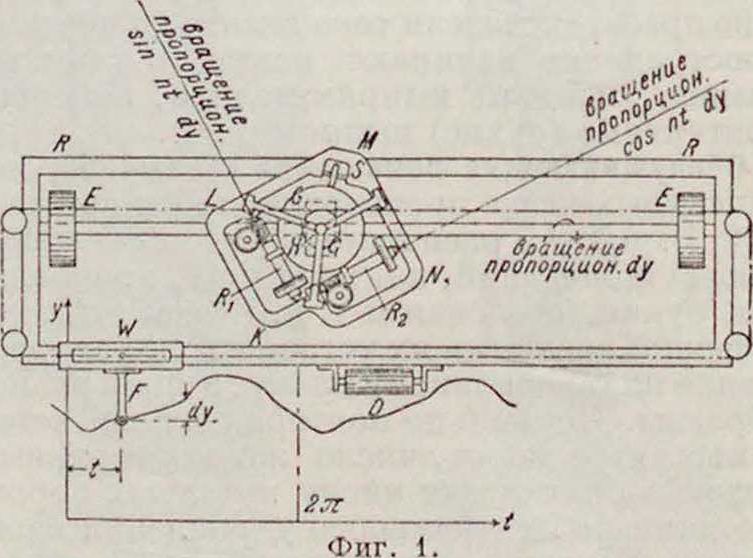
на трех роликах К, Eu I), устанавливается на плоскости (у так, чтобы ось ЕЕ была параллельна оси t. Тележка W со штифтом F свободно скользит по раме анализатора параллельно оси, в то время как штифтом F обводится вычерченная в прямоугольных координатах (t,у) периодическая кривая. Рама RR передвигается при этом параллельно оси у, оставаясь неподвижной, в напра-

плетши /. Движение тележки W пропорционально т. о. (К, движение рамы ЛИ—пропорционально dy. Движение тележки W, ограниченное полным периодом 2π данной периодич. кривой, передается (при помощи серебряного канатика и роликов) шайбе Н со шпинделем S, совершающим п оборотов при прохождении тележкой W полного периода данной кривой. Шпиндель Sзакреплен в интеграторе KLMN, несущем два измерительных колеса Л_г, Л_г, оси которых расположены перпендикулярно друг к другу. При прохождении тележкою расстояния t интегратор вращается т. о. на угол у=nt. Движение рамы, пропорциональное dy—df{i), передается цилиндрической шайбе С, закрепленной на оси ЕЕ.

Эта шайба соприкасается с находящимся над ней стеклянным шаром G и вращает последний вокруг его оси, параллельной оси /. Соприкасаясь с измерительными колесами Л_г π /i ₂, шар G придает им соответственное вращение, определяемое для б’, величиною, пропорциональною si η nt dy, и для Л_г—величиною, про-nopmiona.TibH.costt dy.

Когда весь период 2гг данной кривой будет обведен штифтом F, показания колес Д, и Л_г будут пропорцио-

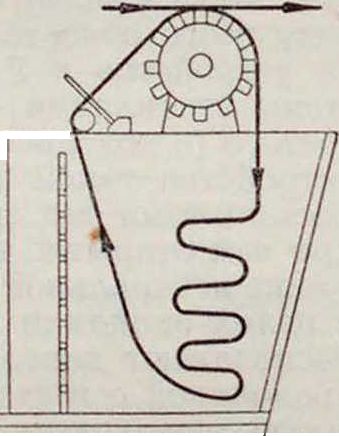
тельных движений, которые могут возникнуть под влиянием сил, изменяющихся по закону данной сложной периодической кривой. На стержне Б насажено свободно вращающееся на шариках колесо М, катящееся по бумаге, на которой вычерчена в полярных координатах анализируемая периодическая кривая. В центре этих координат закрепляется при помощи кнопок кольцеобразная шайба, служащая центром вращения для линейки Е с делениями и для стойки, в которой скользит в радиальном направлении стержень Б. Колесо М ведется по бумаге

Фпг. 2.

так, чтобы указатель К обводил анализи-

2К

иальны величинам sin nt dy и cos nt dy,

о о другими словами, показания измерительных колес Л₁ и Л_г будут равны:

2 It oit

sin nt dy и а_г=p₂ cos nt dy,

о 0

р,и p₂ являются константами, зависящими от размеров прибора; обыкновенно принимают:

Ρι= -7 и ?!= + {

Тогда показания прибора непосредственно равны амплитудам соответствующих простых гармоник и-го порядка данной сложной периодич. кривой, то есть А„=~ и В_п=~.

Анализаторы Генричи-Коради делаются обыкновенно с несколькими интеграторами для одновременного определения составляющих гармоник 1-го, 2-го, 3-го и т. д. порядков. Из других известных систем гармонических анализаторов необходимо отметить анализаторы Мадера, Михельсона, Томсона (лорда Кельвина).

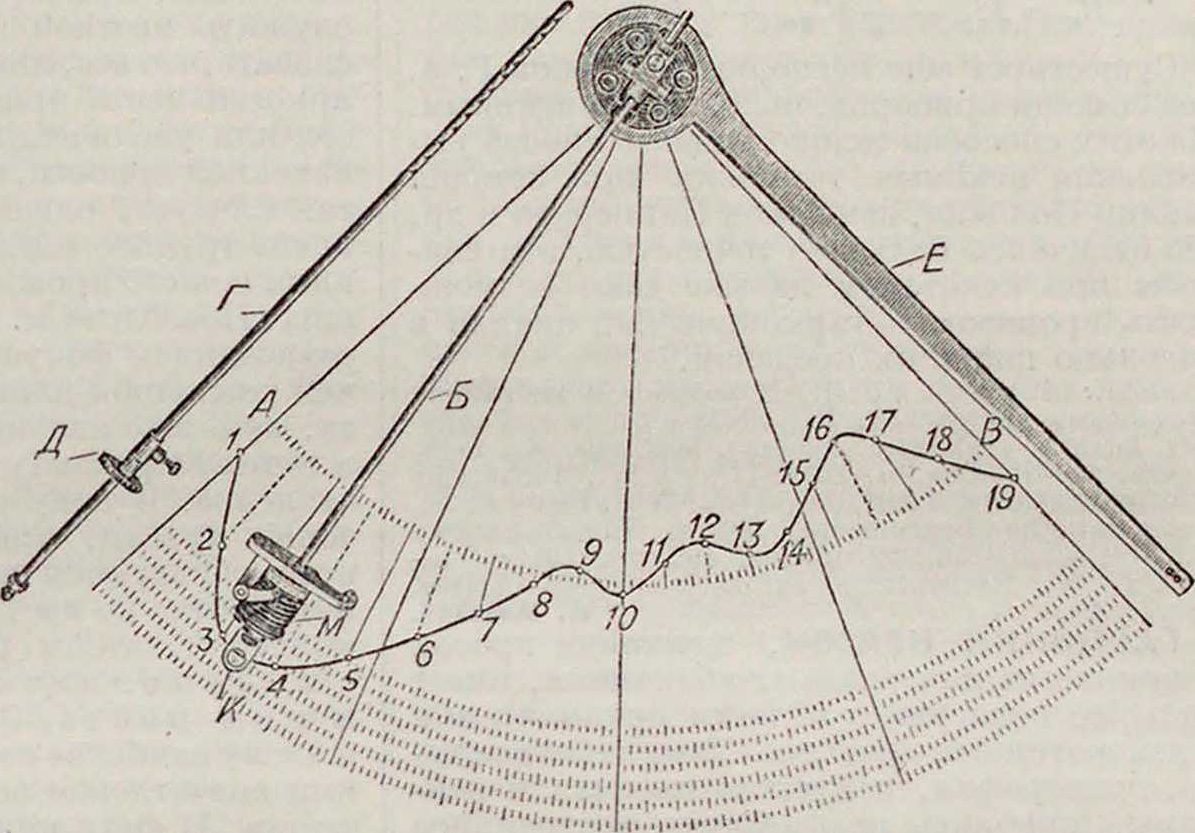
Анализатор, сконструированный Л. К. Мартенсом (фигура 2), отличается тем, что с его помощью непосредственно определяются не коэффициенты ряда Фурье, а амплитуды тех простых гармонических колеба руемую кривую точкою пересечения креста, нанесенного па стеклышке указателя. Стержень Б при этом не вращается, по имеет возможность скользить в радиальном направлении в центральной стойке. На цилиндрической части колеса М нанесены деления, дающие в результате анализа амплитуды соответствующих составляющих гармоник колебательных движений в миллиметров. Для разделения периода исследуемой кривой на необходимое для отыскания соответствующих гармоник число частей употребляется небольшое зубчатое колесо Д па стержне Г. Вставляя последний в центральную стойку вместо стержня Б, обкатывают колесом Д весь период исследуемой кривой на различных расстояниях от центра координат, причем под колесо Д подкладывается копировальная бумага, оставляющая на чертеже мелкие деления, позволяющие разделить период исследуемой кривой на любое количество равных частей. На фигуре 2 показано разделение периода кривой 1—19 на 18 равных частей для отыскания амплитуды синусоиды 9-го порядка. Соответствующие деления колеса Д видны на дуге АВ. Определение этой амплитуды производится след, обр. Данную кривую обводят указателем К слева направо частями 1-2, 3-4, 5-6, 7-8,., 17-18, причем на интервалах 2-3, 4-5 и т. д. указатель К вместе с колесом М приподнимают над бумагой. После этого уже в обратном направлении, то есть справа налево, указателем обводят участки кривой 19-18, Ϊ7-16, 15-14,. .,3-2,пропуская участки 18-17, 16-15 и т. д. Когда указатель будет после этого находиться в точке 2, отсчитываемое на колесе М деление дает амплитуду синусоиды колебательного движения 9-го порядка. Обозначая синусоиду «-го порядка через Р_п и косинусоиду этого же порядка через Рп, получим коэфф-ты ряда Фурье данной периодической кривой.

j — /-> .4 р L р _

^а1П ^J П о ¹ ЗП к ¹ «П

в_п=P

L р__Lp _

s ^{1 3}» ь^{1 5}>*

Существует еще несколько способов Г. а. без помощи приборов, подобных описанным. Из этих способов можно назвать способ вычисления искомых гармоник при помощи таблиц Поллака, шаблонов Ципперера и др. Не отличаясь большою точностью, эти способы при некотором навыке дают возможность производить гармонический анализ в довольно широких пределах.

Лит.: М а р т е н с Л., К вопросу о вибрациях поршневых двигателей, М., 1925; его же, Гармония. анализ, «Техпико-экономич. вестник». М., 1925, 2, стр. 96—99; Сов. П. 3606; II 0 г t W., Technische SchwingungSlehre, 2 ΑιιΠ. В. 1922: W i I 1 e г s F. A., Matliematische Instrumente, Berlin, 1926; Ga Ile A., .Matliematische Instrumente. Leipzig, 1912; I’ol-1 a k L. W., Rechentafeln zur harmoniseben Analyse, Lpz. 1926. Л. Мартенс.