 > Техника, страница 36 > Геодезические треугольники
> Техника, страница 36 > Геодезические треугольники
Геодезические треугольники
Геодезические треугольники, треугольники, па которые разбивается подлежащая съемке часть поверхности земного эллипсоида при больших триангуляциях. Углы в таких треугольниках образуются между нормальными сечениями, а сторонами являются геодезические линии, проведенные, вместо двойственных нормальных сечений, через вершины треугольников (смотрите Геодезическая задача). Длина геодезической линии ничтожно мало отличается от длины нормального сечения (на 1 000 км—0,02 миллиметров), и поэтому только в чисто научных вычислениях вводится длина геодезич. линии вместо длины нормального сечения. Что касается углов между нормальными сечениями и гео-дезическ. линиями и азимутов прямых нормальных сечений, то эти углы следует несколько исправлять. Т. о., между геодезич. сторонами треугольника образуются сферои-дическне углы, при помощи которых можно решить сфероиднч. тр-к. Однако, это решение представляет известные трудности, почему является стремление упростить задачу, сведя ее к решению сферич. или плоского тр-ка. Лежандр показал, что сферич. тр-ки с малыми сторонами, сравнительно с радиусом сферы“ можно решать, как плоские, уменьшив все углы на одну треть сферич. избытка и взяв тс же длины сторон. Открытие этой теоремы необычайно упростило решение сферич. тр-ков. Точно также и для сферои-дич. тр-ков с небольшими, сравнительно с осями, сторонами Лежандр и другие ученые считают возможным заменить решение их решением плоских тр-ков, в которых стороны—геодезич. линии, а углы—сфероидич. углы; при этом необходимо введение трех поправок: 1) на сфероидич. избыток, 2) на кривизну сфероида в вершинах тр-ка и 3) на влияние па величину угла разности длин сторон. Вопрос сводится к нахождению плоских углов А, В, С вместо сфероидич. А, В и С. Необходимо ввести следующие обозначения:
К=-1,- =
г“
1 (1 — e’sin1?)·
— уравнение меры кривизны; а, Ь и с—стороны геодезического и плоского тр-ков; тг=а+ ь‘+ с* —
среднее арифметическое из квадратов сторон треугольников; с — сфероидический избыток над 180° в углах геодезического треугольника; КА, Кп, Кс—меры кривизны в вершинах сфероидического треугольника; к- ка + кп + кс
по— -----„-— — средняя кривизна тре угольника и φ—шпрота.
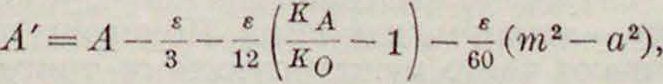
в=в~ е -6 (£®.
з νι κ0
br),
С’
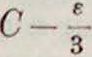
e
12
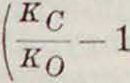
e
60
(m2 — e2).
Последние два члена при треугольниках с сравнительно большими сторонами (например, при определении длины дуги меридиана) еще имеют нек-рое значение, но при тр-ках, непосредственно наблюдаемых в натуре (30— 200 км), значение их ничтожно и не выходит за пределы точности измерений.
Лит.: В и т к о в с к и it В. В., Практическая геодезия, 2 изд., СПБ, 1911; И в е р о н о в И. А., Курс высшей геодезии, 2 изд., М., 1926; Иордан В., Руководство высшей Геодезии, нер. с нем., М., 1881; С л у ц к и 11 Ф. А., Лекции ио высшей геодезии, М., 1894; Ханд р и к о в Μ. Ф., Теория фигуры Земли (Высшая геодезия), Киев, 1900; Д и н г e р Н., Курс высшей геодезии, СПБ, 1898. П. Орлов.