> Техника, страница 37 > Гидравлика

Гидравлика

Гидравлика, наука, изучающая опытным и теоретическим путем явления равновесия и движения жидкостей. Экспериментирование производится как в условиях естественных водоемов и водостоков, так и в условиях искусственных гидротехнических сооружений. Сверх того, устраивают специальные гидравлические лаборатории с искусственным и каналами, водостоками, плотинами, в которых производство опытов особенно удобно, так как все условия опыта м. б. заранее предусмотрены. Так как расход воды при опытах может достигать очень больших размеров, то в современных лабораториях устанавливают замкнутую циркуляцию воды, то есть воду после опытов не отводят в канализационную сеть, а перекачивают и используют вновь; т. о. расходование воды из водопровода сводится к минимуму. Из существующих в СССР гидравлич. лабораторий можно указать на лаборатории: Центрального аэрогидродинамическ. ин-та в Москве с одним из самых больших искусственных каналов в мире; Московской сел.-хоз. академии имени К. А. Тимирязева; Московского ин-та инженеров транспорта; Ленинградского политехническ. ин-та; Ленинградского ин-та инженеров путей сообщения; Донского политехнич. ин-та (в Новочеркасске).

Жидкости разделяются на капельные и газообразные. Идеальной капельной жидкостью называется несжимаемая жидкость, лишенная вязкости; идеальным газом называется газ, лишенный вязкости и вполне точно следующий закону Бойля-Мариотта. Вода и воздух при обыкновенных условиях близки по своим свойствам к идеальным жидкостям. В идеальных жидкостях псе внутренние напряжения приводятся к давлениям, направленным нормально к по верхностям. Чтобы учесть свойства реальных жидкостей, Г. вносит полученные эмпирическим путем исправления в результаты, выведенные первоначально для идеальных жидкостей. Т. к. законы гидростатики вообще можно без изменения прилагать к реальным условиям, то наибольшее внимание отводится в Г. вопросам движения жидкостей. Последующие рассуждения относятся к жидкостям однородным, то есть к таким, плотность ρ в каждой точке которых может зависеть явно лишь от давления р в той же точке, в том случае, когда плотность под влиянием давления может изменяться (упругие жидкости), или же является величиной постоянной, если перемена давления не меняет объёма жид-кого тела (капельные жидкости).

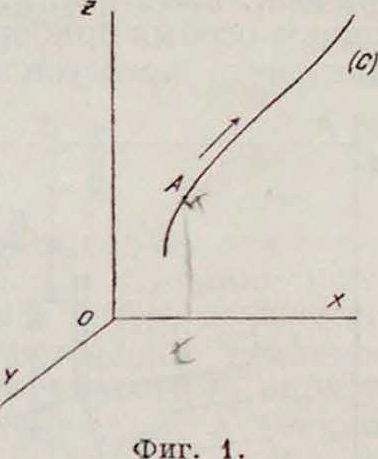
Движение жидкости называется установившимся (перманент н ы м), если во всякой точке пространства проходящие через нее частицы жидкости все время приобретают одни и те нее скорость, плотность и давление, определенные для рассматриваемой точки пространства. Установившееся движение жидкости совершается по л и-н и я м тока — неизменным траекториям жидких частиц. Если какая-нибудь частица, находившаяся в момент t в точке А (фигура 1), описала затем траекторию (С), то все частицы, прошедшие через точку А позже или раньше этой частицы, описывали ту же самую траекторию или линию тока (С). Отнесем движущуюся жидкость к прямоугольной системе осей координат OXYZ (фигура 1). Обозначим через р давление жидкости, через ρ—плотность, через м, ν, го—компоненты скорости по осям координат, через U— силовую функцию. Количества ρ, ρ, и, а, w, U для установившегося движения суть функции координат х, у, ζ рассматриваемой точки пространства; эти количества связаны между собою некоторым соотношением, представляющим интеграл ур-ий движения жидкости, называемый интегралом Д. Бернулли (смотрите Гидродинамика):

J ^dp=Const + U - -у (и“ + а² + и·³). (1)

Это соотношение имеет место вдоль любой линии тока; произвольная постоянная определяется по значениям функции в какой-нибудь точке рассматриваемой линии тока. При переходе с одной линии тока на другую значение постоянной вообще может меняться. Если жидкость несжимаемая и действующая сила есть сила тяжести, то ρ—постоянно, и U= — gz, если ось OZ направлена вертикально вверх; в этом случае уравнение (1) принимает вид:

f=Const - gz- -i-F», (2)

где V есть скорость (V²=м“+п“+мг^!). Если в какой-нибудь точке линии тока измерены

p, z, V (например: р„, z₀, F₀), то уравнение (2) примет в ней следующий вид:

у=Const -gz₀- V

Вьгчтя это равенство из (2), разделив результат на <7 и введя вес единицы объёма жидкости у=ад, получим:

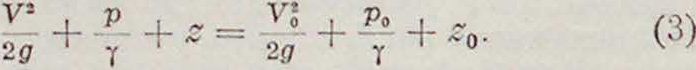
Это соотношение имеет место вдоль всей рассматриваемой линии тока и представляет в обычно применяемом в Г. виде выражение закона Д. Бернулли. Уравнение (3) может быть представлено в виде:

^г + у + д — Const. (4)

Три члена левой части имеют измерение линейной величины. Член г называется высотою относительно горизонта. или ниве л и р н о и высотой, член --- —

пьезометрич. высотою, член ^ ’ —

высотою соответствующей скорости, или скорости ы м напором. Ур-ие (4) показывает, что вдоль каждой линии тока сумма трех высот: нивелирной, пьезометрической и скоростной постоянна. Пьезоме-трическ. высота м. б. легко измеряема с помощью особых приборов—п ьезо метров. Пьезометр представляет обычно открытую

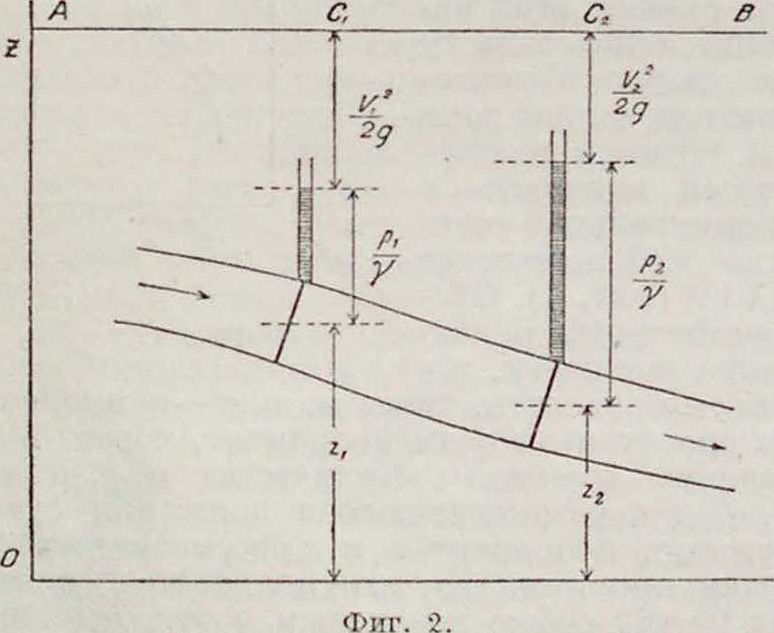
с обоих концов трубку, прикрепленную одним концом к стенке сосуда, внутри которого течет жидкость. Необходимо, конечно, наблюдать за тем, чтобы установка пьезометров не меняла характера течения жидкости ; для этого во всяком случае отверстие в стенке, ведущее в трубку, должно быть мало, и трубка своим концом не должна входить внутрь сосуда (фигура 2). Плоскость АВ, на которой лежат точки С, б,.—концы отрезков, представляющих суммы трех высот, называется плоскостью напора. Если z измеряется до ц. т. сечения сосуда, то пье-зометрическ. высоту надо отмерять от этого центра тяжести. Пьезометрическая высота, сложенная сдавлением атмосферы, равна давлению, имеющему место в точке, от которой пьезометрическая высота отмеряется. Очевидно, чго в тех местах, где сечение сосуда шире и, следовательно, V—меньше, должно быть больше р, и наоборот.

Ф-ла (3) выведена для случая идеальной жидкости; для реальных жидкостей геометрическое место точек С, С“,. не представляет горизонтальной плоскости: точка лежит ниже точки С, и т. д. Это объясняется тем, что вследствие сопротивлений происходит постепенная потеря напора вдоль течения жидкости. Опыт показывает, что можно положить:

2(7

Р, „ V*

γ ‘ ~0 ~ 2(7 ⁺

(5)

Ур-ие (5) есть ур-не Бернулли для несовер-

уз

шенных жидкостей. Член ζ- называется потерянным напором, а коэфф. ζ— к о э фф и циентом сопротивле и и я; Гость скорость струи в месте, непосредственно следующем за местом, где произошла потеря напора. Наиболее прост тот случай, когда потеря напора происходит от резкого увеличения сечения струи; в этом случае наблюдается резкое изменение скорости, и происходит то же самое явление потери энергии, какое имеет место при ударе тел. В применении к капельным жидкостям определение потери напора от резкого .увеличения сечения струи, или, как говорят, от гидравлического удара, составляет содержание теоремы Борда-Карно; именно, можно показать, что эта потеря напора η равна напору, соответствующему потерянной скоро сти, т. e.=где Ту —скорость до удара, а V—непосредственно после удара; теоретически выведенная потеря напора исправляется опытным коэфф. «(=1,04—1,2). Таким образом в этом случае формула Бернулли получает вид:

+ Ι + _α<Ζ=ΖΤ. (6)

г ¹ 2(7 ^к

Существуют и несколько отличные формулы для η, например, формула Мизеса (Mises):

vi i p· > „ _ ν·, p

2У + 7 + -¹— 2g +

Значительное выяснение характера движения реальной жидкости сделано О. Рейнольдсом (Osborne Reynolds). Когда жидкость течет, например, в цилиидрич. трубе, то движение ее происходит спокойно, параллельными струйками, или, как говорят, бывает ламинарным, если скорость жид-кости не превосходит определенного предела, зависящего от диаметра и поверхности трубы, рода и физического состояния текущей жидкости. Если скорость жидкости превзойдет эту предельную, или, как ее назвал Рейнольдс, крит и ческую скорость, то движение делается турбулептиым, то есть внутри жидкости начинают образовываться вихри; эти вихри зарождаются в пограничной поверхности, отделяющей топкий, примыкающий к стенкам трубы слой, в котором движение остается ламинарным, от внутренней области, в которую уносятся образовавшиеся вихри, и где таким образом имеет место вихревое движение (смотрите Вихревая теория). В тонком слое с ламинарным движением частицы жидкости, непосредственно прилегающие к стенкам трубы, имеют скорость, равную пулю; внутрь трубы скорость увеличивается и на границе области ламинарного движения делается рав ной критической. Следствием турбулентного движения является пульсация струй, то есть постоянное колебание скорости в каждой точке около некоторого среднего значения, а также зигзагообразное движение жидких частиц, увлекаемых в то лее время в общем движении потока. В уравнениях Павье (Navier) движения вязкой жидкости

(смотрите Гидродинамика) член -, зависящий от

L V* г инерции, имеет размерность _г,=_у, где L—

длина, Т—время, V—скорость; зависящий от вязкости член

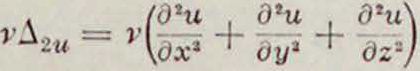
1 V

имеет размерность v _т= v — Так как оба члена входят слагаемыми в одно и то же уравнение, то размерность их доля-сна быть одинакова, поэтому отношение их должно быть отвлеченным числом Н:

Это число называется ч и с л о м Рей-нольдса; здесь V есть характеризующая поток скорость выше критической, L—линейная величина, характеризующая линейный размер потока, v — коэффициент вязкости жидкости. Для круглой трубы нижний

предел И о“ 2 000. Введение числа Рейнольдса позволило устанавливать механическ. подобие жидких потоков; общий признак подобия такой: если вычисленные для двух потоков но значениям V, L, v числа Рейнольдса между собой равны, то потоки механически подобны; в частности, два жидких потока в одной и той ясе среде механически подобны, если VL для них равны ме-яеду собой. Эти выводы имеют громадное практическое значение, так как позволяют от одного течения, например, выполняемого экспериментально, перейти к любому другому, ему механически подобному. Например, в трубе с диаметром в 30 сантиметров совершается течение воды со скоростью 80 см/ск. Какую скорость надо придать воде в такой же трубе, ио с диаметром в 20 см, чтобы движе-пие было механически подобным? Так как в обоих случаях v равны между собою, то Д. б. 80-30=К-20; отсюда К=120 см/ск.

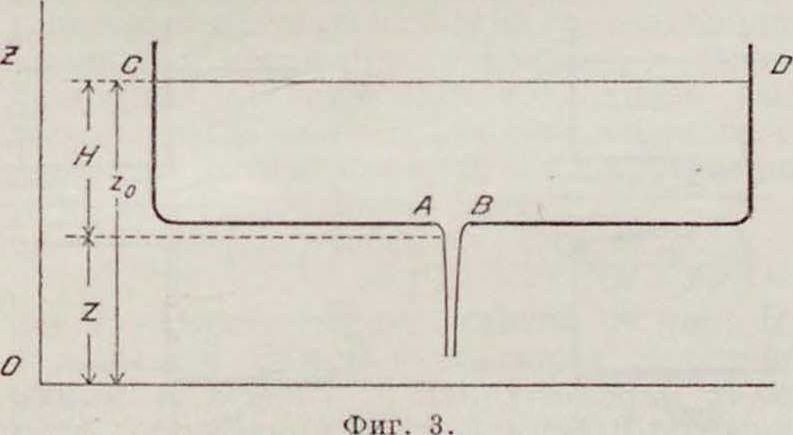
Изложенные выше общие результаты прн-меняются к исследованию истечения жидкости из сосудов через отверстия, сделанные в тонком дне или тонкой стенке сосуда, через отверстия с насадками и через водосливы. Возьмем сосуд, в дне которого сделано отверстие (фигура 3); площадь CD

сосуда настолько велика сравнительно с площадью отверстия, что без особых погрешностей может быть принята бесконечно большой. В сосуд налита жидкость, которая вытекает из отверстия АН; давление на свободную поверхность жидкости сверху сосуда и на струю равно р₀. Требуется найти скорость истечения V_l жидкости. Применяя теорему Бернулли, получим:

р ₊ 2> _{+ гь =} У1 ₊ л

20 1 ⁰ 2 3 7

где левая часть отнесена к свободной поверхности z=z₀ и правая—к сечению струи по выходе из сосуда. Так как на свободной поверхности можно, вследствие большого размера площади CD, положить V₀=0, то, полагая z„~z=Н, из предыдущей формулы получаем:

F,=Vigti. (8)

Эта формула дана Торичелли в 1643 году; из нее следует, что приобретенная жидкостью скорость равна скорости падения тяя-селого тола с высоты Н. Если площадь CD конечна и равна ω₀, а площадь сечения струи под Л В равна ш, то условие равенства расхода Q дает: ζ>=ω₀Ε₀=α»Ε, где V— скорость жидкости под отверстием; при этих условиях, если давление на струю равно р, из уравнения Бернулли получим:

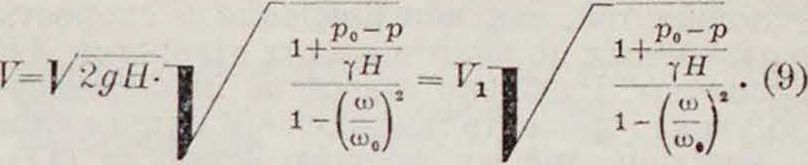
Условия, из которых выведены эти ф-лы, не соответствуют реальным условиям истечения жидкости. Прежде всего, вследствие вязкости, скорость V истечения реальной жидкости всегда меньше скорости F, определяемой по формуле Торичелли, а именно:

V=χρ V, — грУЛдЫ, (10)

где ψ в среднем равно 0,97. Так. обр. истечение происходит как бы иод действием меньшего напора //, определяемого условием:

V= Ψ УцЩ=Vigil г, Н_х=ψ" II; отсюда получаем высоту сопротивления

&-НИ) ΪΗ£·

где ξ—коэффициент сопротивления, равный в среднем 0,063, ψ—коэффициент скорости. Сверх этого, есть еще другая существенная погрешность в формулах (8) и (9). Жидкость, подходя к отверстью АН, не идет параллельными струйками, и ниже отверстия АН образуется сжатие струн (фигура 4). Если за площадь сечения струи, для которого вычисляется V, принимать даже наиболее сжатое сече- ^фиг. 4. ние ее, где можно считать отдельные струйки идущими параллельно между собой, все же скорости этих отдельных струек различны, и давление внутри струи различно, повышаясь от наружных частей ее внутрь. Поэтому предположения, из которых мы выше исходили, что давление внутри струи всюду одинаково и расход Q

определяется формулой Q=mV, неверны. Отношение сЬ площади сечения струи в ее наиболее сжатом месте к площади отверстия называется коэффициентом сжатия, и если, несмотря на неодинаковость скоростей у различи, струек, определять расход Q из формулы Торичелли, придется в связи с данными опыта вместо ω брать кт, так что Q — αψω УЛдН=μ<ο У2дН· (11)

Коэфф-т μ=сггр называют к о э ф ф - т о м расхода. Для круглых отверстий в тонкой стейке молено в средне.м взять α= 0,64,

а так как ψ=i —.=i —?-=0,97, то

^Ύ V 1 + С у 1+0,063

для таких отверстий μ — 0,62. На коэффициент сжатия а влияет форма сосуда; для дна, вдавленного около отверстия внутрь жидкости, к меньше 0,64 и может доходить до 0,5, а для дна, вытянутого вдоль течения жидкости, а > 0,64 и может быть близким к единице. Для круглых отверстий при различной форме дна Вейсбах дал табл, значений μ на основании опытов; Цейнер объединил эти результаты в эмпирич. ф-ле: μ=μ„ (1 + 0,33214 cos³ β + 0,16672 cos· β), где β—угол, составляемый дном сосуда с его осью, μ_а—значение μ для β=90°.

Если истечение происходит из отверстия в боковой стенке сосуда (фигура 5), то задача усложняется, так как давление и скорость в различных по высоте частях отверстия А В различны. Разбивая отверстие на бесконечно узкие горизонтальные сечения, применим к каждому такому сечению формулу (11), где ω будет равна у dz. Получим для элементарного расхода dQ через выделенное сечение выражение: dQ=gyyZgz dz и для полного расхода я

Q=уУ2.фУ^ dz. (12)

h

Связь между у и z должен быть установлена формою отверстия; коэфф. μ приходится определять из опытов. Однако большей частью пользуются формулою

(2=μυγ2ίμ₀, (13)

где ζ₀ — координата центра тяжести отверстия, ω—площадь отверстия, а μ — определяемый из опыта коэффициент расхода. Опытные определения коэффициента производили Понселе, Лебро и Вейсбах. Для прямоугольного отверстия с измерениями: а— высота (вдоль вертикали), b—ширина, h— глубина верхнего края отверстия под уровнем жидкости, по этим опытам:

Q=μαΐ) y%gz₀,

при чем z₀ — h+ £, а μ указано в следующей таблице:

Значение коэффициента расхода μ.

а в см h в м	20	10	5	2	1
0,05	0,58	0,60	0,62	0,64	0,68
0,5	0,60	0,62	0,63	0,63	0,65
1,0	0,60	0,62	0,63	0,63	0,63
3,0	0,60	0,60	0,61	0,61	0,61

Если истечение происходит через отверстие в толстой стенке или через отверстие с насадками, то предыдущие результаты должны быть изменены. Насадками, или м ундштукам и, называются короткие трубки, приставленные к отверстию, через к-рое выливается жидкость; насад- -

кп являются существенными частями инжекторов, ^А

водоструйных насосов идр. приборов и аппаратов. в

Насадкой Вентури называется цилинд-_

рическая трубка, приставленная с фигура 5.

наружной стороны к сосуду (фигура 6) горизонтально или наклонно к горизонту. Жидкость, протекая через насадку Вентури, сначала сжимается, а потом расширяется и заполняет всю трубку; поэтому коэффициент сжатия а в этом случае равен единице; коэфф. расхода μ оказывается равным 0,82. Таким образом насадка Вентури почти на 30% повышает расход, но зато дает до 7% потери живой силы струи и большую потерю напора на преодоление сопротивлений при протекании воды

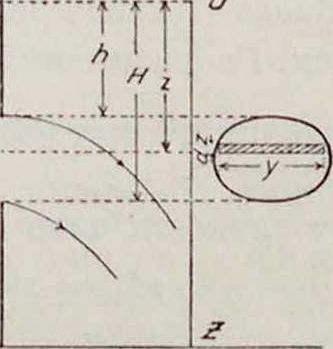
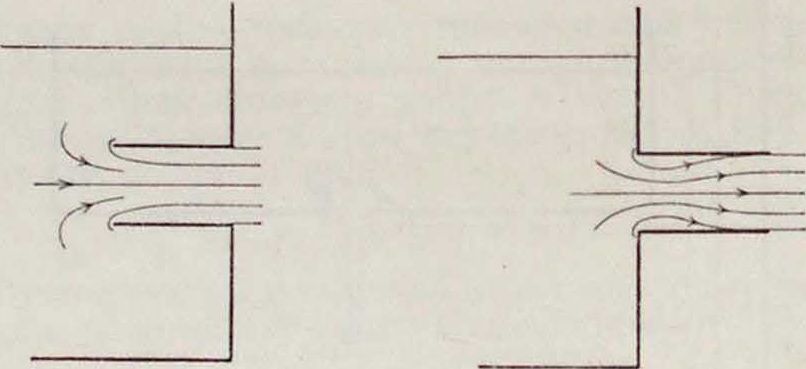
Фигура 6. Фигура 7.

через насадку. Насадка Ворд4 представляет, напротив, короткую цилиндрическую трубку, входящую внутрь жидкости (фигура 7). Если толщина стенок насадки мала, то коэффициент расхода μ близок к 0,54. К о ii и ч е с к а я и ас ад к а, суживающаяся в направлении течения жидкости (фигура 8), повышает коэфф. расхода /<> незначительно изменяя скорость V, сравнительно

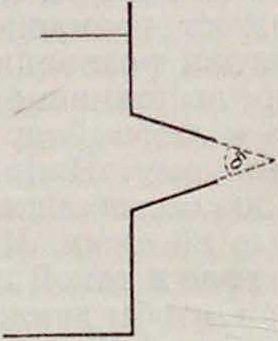
Фигура 8.

с истечением из отверстия в тонкой стенке; поэтому такие насадки употребляются в брандспойтах. Коэффициент μ зависит от угла схода δ и имеет максимум в 0,946 приблизительно при δ — 13,5°.

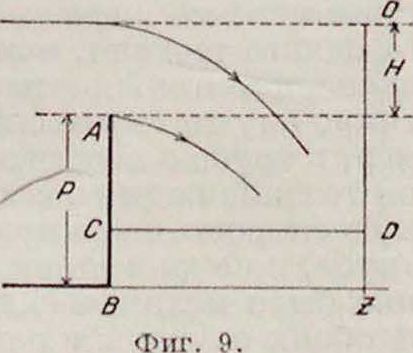
Особо важное значение имеет истечение воды через водосливы (смотрите), то есть такие отвер-

стия, у которых верхней кромки нет или она не соприкасается с жидкостью (фигура 9); стенка АВ водослива называется порогом. Водосливные отверстия делают б. ч. прямоугольными или по форме трапеции. Если водослив прямоугольный и его ширина равна Ь, то в формуле (12) надо положить у — b, h — 0, и мы получим для расхода через водослив выражение:

Q=-| μ ЬП]/2дН.

Эту формулу предпочитают применять, вводя числовой коэфф. ²/з в к, в виде:

Q=/ЛИ ]/2дН, (14)

при чем коэффициент μ определяется из опытов. Если уровень А порога А В лежит выше уровня СВ воды в отводящем канале, то водослив называется совершенным, полным или н е з а т о п л е н н ы м; если же кромка А подтоплена водою отводящего канала, то водослив называется несовершенным, неполным или затопленным. Случаи истечения воды через водосливы весьма разнообразны. Приходится различать истечения через пороги с тонкой стенкой и толстой стенкой; существенное значение имеют: величина напора II, образование между порогом и струей разрежения или сжатия воздуха, подтопление отходящей струи. Все эти случаи приходится изучать большей частью эмпирически и для каждого типа водослива устанавливать коэффициент расхода μ. Весьма обширные исследования водосливов были выполнены Вазеном. Для совершенного водослива с острой кромкой и с доступом воздуха под струю Базен дает:

[0,405 + °-^] [1 + 0,55 щ^г],

где Р—высота порога, считая от дна; Ή и В даны в м. Весьма часто порог делают широким и кромку А закругленной; такого рода сооружения применяются в водосливных плотинах. Коэффициент расхода μ для таких водосливов выше, чем для водосливов с острой кромкой. В случае необходимости повысить расход воды через водослив, приходится иногда делать их длину больше ширины реки; для этого водосливам, перегораживающим реку, придают форму ломаной или кривой линии.

Изучение движения жидкости в трубах имеет громадное практическое значение. Построение водопроводов, канализационных сетей, нефтепроводов, газопроводов невозможно без знания законов движения жидкостей по трубам. Обычные условия движения воды в водопроводах дают турбулентное движение, но в Г. применяют формулу Бернулли и к движению жидкости по трубам, вводя среднюю скорость в каждом сечении. Сопротивления при движении в трубах бывают двух родов: сопротивление от трения и особые сопротивления, вызываемые изменениями геометрической формы трубопровода. Рассмотрим сначала сопротивление от трения. Пусть по цнлиндрич. трубе протекает в установившемся движении жидкость, заполняя всю трубу доверху (фигура 10). Обозначая среднюю скорость потока через V,

давления в сечениях А₀ и А соответственно через р„ и р, имеем по формуле Бернулли:

р или

^ν“, Р., „ -V*

20 + γ + ^л° ~ Тд +

+ ζ + у,

где η представляет напор, потерянный на пути L вследствие сопротивлений. Опыты показали, что η не зависит от давления и мо-асет быть представлено ф-лой:

_η=ί.ψΐ, (15)

где II—периметр сечения трубопровода, о>— площадь сечения, L—расстояние между рассматриваемыми сечениями и ДБ)—функция средней скорости V, оп- _{Δ л}

ределение вида которой и составляет основную задачу в изучении трения. Отношение на зывается иногда сред- _{фпг 10}_

ним гидравлическим радиусом сечения: для круглой трубы он равен четверти ее диаметра. Потеря напора J на единицу длины трубы равна: п /ГУ) т

Функцию ДБ) иногда представляют в виде:

ДЮ=?₁^; (19)

_т η л J-_r =

в этом случае задача сводится к определению коэфф. ζ_χ. Предложено очень много выражений для функции f(V). Укажем некоторые. Формула Дюпюи имеет вид ДБ) =

_{( ГД}е λ=0,0302. Отсюда получаем для круглых труб:

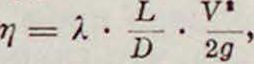
где Л—диаметр в м, L—в м, —в м/ск. Вводя расход Q в м“/ск, получим: Б =

О*

и отсюда η — β д, L, где β приблизительно равно^₀. Формула Дарси:

Д7)=у(а+ 1)V

где α= 0,0002535 и 6=0,000006478 для новых чугунных труб; для старых труб эти коэффициенты должен быть увеличены. Эта формула неоднократно применялась при постройках наших водопроводов. Формула Фламана:

Д7)= 0,00023 у j/Xl,

где V и В должны быть выражены в м. Для капиллярных трубок имеет место закон, установленный опытным путем Пуазейлем (Poiseuille): потеря напора J на единицу длины равна:

_т _ Vo-v _ 32 vV ^J fL g D‘ ’

где v—коэфф. вязкости. Для воды найдено: ν (в е.н /ск)=0,0178 при 0°, 0,0133 при 10°, 0,0100 при 20° и 0,0056 при 50°. Этот закон м. б. получен и теоретическим путем.

Особые сопротивления имеют место при входе жидкости в трубу, при резком изменении сечения трубы в местах ее изгиба, при ответвлениях. Во всех этих случаях принимается, что потеря напора ?; выра-жается ф }рмулою η—ζ₂, где ζ₂ для каждого типового случая имеет свое значение. Таким образом совокупность всех потерь напора при движении по трубопроводу м. б. представлена в виде:

2д ’

(17)

где все коэфф-ты ζ должен быть отнесены соответственно к скоростям, получающимся непосредственно после испытанного жидкостью сопротивления. Эти результаты применяются при расчете водопроводов (смотрите Бодоснаб-oiceuue). В нефтепроводах специальную задачу представляет подача тяжелых сортов нефти, перекачка которых требует больших давлений; сверх того, при охлаждении эти сорта нефти настолько густеют, что движение их по трубам может остановиться.

Стенки трубопровода должны быть настолько толстыми, чтобы выдерживать не только нормальное внутреннее давление, под которым вода течет в водопроводных трубах, но и резкое увеличение давления, называем, гидравлическим ударом. Гидрав-лич. удар в водопроводной трубе получается в том случае, когда вследствие быстрого запирания кранов или задвижек происходит резкая остановка движения колонны воды в трубе. При этом около задвижки давление значительно повышается; вследствие упругости воды и стенок трубы, которые расширяются в местах повышенного давления, это состояние воды и трубы передается вдоль трубы по закону колебательных движений. Подробное исследование вопроса о гидравлическ. ударе как теоретическое, так и опытное, вполне выяснившее все его стороны, было выполнено проф. Η. Е.-Жуковским []. Оказалось, что гидравлическ. удар распространяется вдоль водопроводной трубы с постоянной скоростью, величина которой для одной и той лее трубы не зависит заметно от силы удара; эта скорость зависит от вещества трубы и от отношения толщины ее стенок к диаметру трубы. Величина гидравлического удара пропорциональна потерянной при ударе скорости течения воды и скорости распространения ударной волны в трубе. Опасное возрастание ударного давления происходит при переходе ударной волны с труб большого диаметра на трубы меньшего диаметра; достигнув конца тупиков, сила ударного давления удваивается. Простейшим способом ограждения водопровода от гидравлических ударов является приспособление для медленного закрытия кранов, причем продолжительность закрытия должна быть пропорциональна длинам труб. Точно так же защищают от гидравлического удара воздушные колпаки надлежащих размеров, поставленные при кранах и задвижках; однако, сохранение воздуха в колпаках является затруднительным.

Движение воды (смотрите) в каналах и реках чрезвычайно сложно; не только скорости различны в различных местах каждого живого сечения, но даже в одном и том же месте одного и того же живого сечения скорость все время меняется по величине и направлению, колеблясь около некоторого среднего значения. Поэтому для практических целей обыкновенно вводят среднюю скорость V потока, определяя ее из условия, чтобы расход Q в единицу времени (секунду) был равен средней скорости, умнозкен-ной на площадь живого сечения:

Q=V-to. (18)

Если соединить мезкду собою точки живого сечения, в которых скорости одинаковы, то получаются линии, называемые и з о т а-х а м и. При спокойном состоянии воздуха наибольшая скорость при симметричности живого сечения находится около середины потока на расстоянии около Vs глубины низке свободной поверхности, ес ш ноток достаточно глубок; в потоках небольшой глубины она ближе к свободной поверхности. Средняя скорость находится на расстоянии О,С глубины от свободной поверхности. Наименьшая скорость V имеет место у дна и берегов (см.

Гидрометрия). Необходимо, однако, заметить, что всякие неровности и неправильности дна и берегов и искривления русла существенным образом изменяют распределение скоростей; точно так же существенное влияние на распределение скоростей имеет ветер. Если средняя скорость вдоль некоторого участка водостока постоянна, то говорят, что на этом участке имеет место равномерное установившееся движение. Существуют формулы, позволяющие определять среднюю скорость потока V по среднему гидравлич. радиусу

11 — “ и по уклону г. Рассмотрим небольшой участок канала или реки (фигура 11) длиною АС — L, вдоль которого уровень воды равномерно понижается па величину h. Тогда, обозначая угол наклона свободной поверхности воды к горизонту через г, получим вследствие малости угла: л.

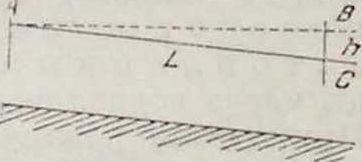
Фигура 11.

г =

L ’

(19)

очевидно, что, при топ же степени точности, за длину L можно принять расстояние АВ. Отношение h L называется относите л ь-н ы м падение м, или уклоном. Уклоны обыкновенно очень малы: для среднего плеса Волги г=0,000044; для Днепра в области порогов г=0,000080; для ирригационных каналов г берется от 0,0002 до 0,0005.

Приведем некоторые формулы для определения средней скорости V. Формула Ше-зи (Chesy, 1775 г.):

V=суж,

где с—постоянный коэффициент; по Тадипн, можно положить с=50. Однако, более точные наблюдения показали, что с нельзя считать постоянным; отсюда возникли другие формулы. Формула Гангилье и Куттера (Ganguillet ei Kutter):

23 +

V —

ι +

0,00155

1 ш,

) У ii

здесь η—к о э ф ф. шероховатости, изменяющийся от 0,01 (для каналов с очень гладкими стенками) до 0,04 (для естественных водостоков с заросшими земляными стенками). Ф-ла Форхгеймера (Forchheimer):

У — ¹ II 0,7. i 0,5

П *

где п—указанный выше коэффициент шероховатости. Ф-ла Базена:

V= ⁸⁷ Λ УЖ,

1 + -7=

V а где β — коэфф-т шероховатости, изменяющийся от 0,00 (для гладких стенок) до 1,75 (для очень шероховатых). Существуют и другие формулы, в которые не входит коэфф. шероховатости, но в которых зато учитываются глубина и ширина канала; таковы, например, ф-лы Зидека (Sieclek), Лнпдбое (Lindboe), Германека (Пегшапек). Из ф-лы для расхода

Q=Va>=сш У Яг (20)

следует, что, желая для данного расхода иметь наименьшее поперечное сечение канала, необходимо выбрать такую форму живого сечения, чтобы К было наибольшим. Это будет достигнуто, если профиль канала будет полукруглым, что часто и осуществляется в железобетонных каналах; профилю земляных каналов обычно придают форму трапеции с наклоном стенок, определяемым связностью грунта. Формулы (19) и (20) применяются при расчете каналов (смотрите).

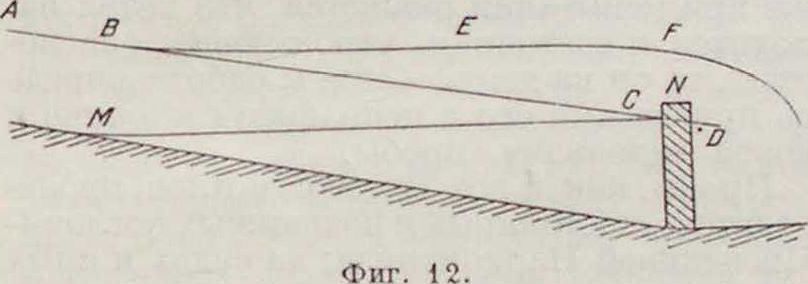
Рассмотрим теперь случай установившегося неравномерного течения, когда средняя скорость Уменяется при переходе от одного живого сечения к другому. Такой случай может, например, иметь место, когда вода в своем течении имеет в каком-нибудь живом сечении преграду, через которую она переливается (фигура 12). Тогда равномерное течение нарушается, и вместо свободной поверхности ABCD получается поверхность ABEF; т. обр., начиная с точки В, лежащей вверх по течению, происходит подъем свободной поверхности, и образуется так паз. подпор, или подпруда. Линия BEF называется подпрудной кривой, а расстояние FB—д л и л о ю или гидро-дина м и ч е с к о и а м п л и т у д о и подпруды. Если бы течения не было, то вода стояла бы на уровне MN, причем вверх от точки М затопления уже не было бы. Линия MN называется гидростатичес-к ой а м п л и т у д о и подпруды. Амплитуда гидродинамическая больше амплитуды гидростатической; это необходимо иметь в виду для определения площади затопления при постройке плотин. При малой глубине и большой скорости течения может образоваться порог, или п р ы ж о к, воды, когда происходит резкое повышение уровня с соответствующим понижением скорости (фигура 12). Обозначая скорость до порога че рез V и после порога через V₁, приблизительную высоту порога h можно вычислить по формуле:

7_<=1L(F*-^);

чтобы порог образовался, необходимо, чтобы глубина до порога была меньше. Прыжок воды может получиться, когда вода вливается в канал или из более узкого канала или из сосуда, или когда она вливается в канал,переливаясь через водослив. В случае широкого и неглубокого прямоугольного канала можно для неуста-повившегося движения составить дифференциальное ур-ие кривой продольного профиля. Направляя ось О У вертикально вверх и отсчитывая элементы длины ds вдоль дна канала, будем иметь ур-ие:

dy _. у“-я;

ds ¹ у“-я; ’

где Л₀, И_х—нек-рые постоянные; в зависимости от значений г, 11₀ и //, интеграл этого уравнения даст или подпрудиую кривую, или прыжок, или некоторые другие формы свободной поверхности воды.

Лит.: ) Ж у к о в с к и ii Η. Е., О гидравлич. ударе, еЗаписии Академии наук по физико-матема-тнч. отделению», т. 9, 5, СПБ, 1900; Μ а к силе κι; о Ф. К., Курс гидравлики, М., 1921; Астров А. И., Гидравлика. М. 1911; Саму сь А. М. Тех-иич. гидравлика, М.—Л. 1926; Пинегин ΓΙ. II., Гидравлика, Одесса, 1925; Fore h li с i m er 1’., Hydraulik, Leipzig, 1914; Г 0 s c h I T., Lelirbuch der Hydraulik, Berlin. 1 924: К 1 a m a n t A., Micanique appliquie. Hydraulique. 3 id., Paris, 1909: limis s i-N i s ij .1. Essai sur la thCorie des eaux courantcs, P„ 1370; сокращ. изложение этого обширного труда см. Б о б и лев Д., Очерк теории водяных течений, выработ. Буссннеском, СПБ, 1898. А. Некрасов.