 > Техника, страница 38 > Гипербола
> Техника, страница 38 > Гипербола
Гипербола
Гипербола, кривая 2-го порядка (смотрите Конические сечения). Ее уравнение в канонической форме имеет вид:
Кривая состоит из двух ветвей, уходящих в бесконечность (фигура 1). Если система координат прямоугольная, то оси координат в этом случае являются главными осями Г.: ось ОХ—действительной, ось ОΥ—мнимой осью; величина 2а называется длиной действительной оси, а 26—мнимой оси I. Точки пересечения Г. с действительной осью Л
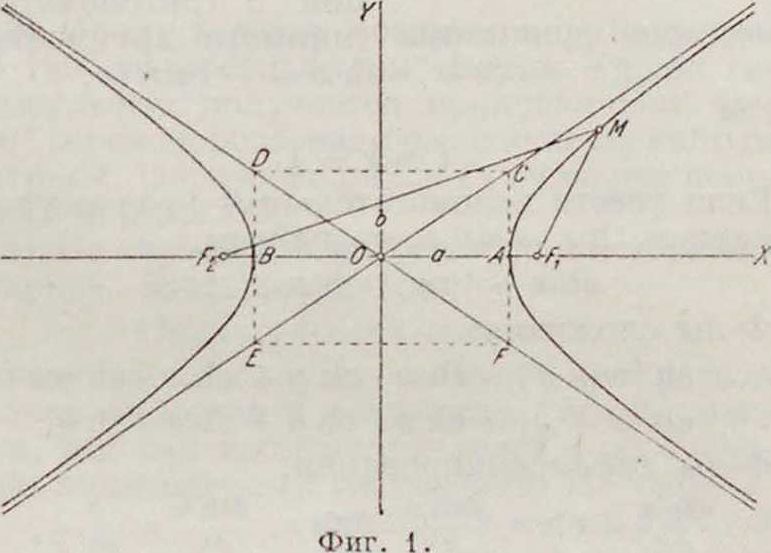
и В называются вершинами Г. Начало координат О есть центр Г. Точки Ft и F2, лежащие на действительной оси на расстоянии c=/a‘-rb- от центра называются фокусами. Г. может быть определена как геометрическ. место точек, разность расстояний которых до двух фокусов есть величина постоянная, равная 2а; MF*—MFl=2a. Диагонали прямоугольника CDEF, построенного на осях Г., являются ее а с и м и т о-тами; при удалении в бесконечность ветви Г. безгранично приближаются к асимптотам (см.
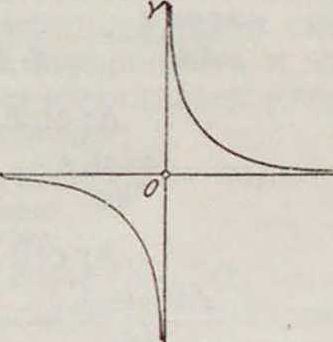
А симптотическое пр χιό лужение). Если действительная и мнимая ось равны (а=6), Г. называется равнобоч-н о и; ее асимптоты образуют с осями коорди- фиг 2
пат углы в45° и взаимно перпендикулярны. Ур-ие равнобочной Г. получает особо простой вид (фигура 2), если за т оси координат взять асимптоты: у=χ ·
Лит.: см. Аналитическая геометрия. 3. Степанов.
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ суть: синус гиперболический от ж (sinti х, или sh х, или ©in х), косинус гинерболическ. (cosh ж, или ch х, или Sosa;), тангенс гиперболич. (tgh х, или thx, или (Eg х), котангенс гиперболич. (cth ж, или Sotg X). Они определяются формулами:
sh х —
сх — е~х £
ch х =
ех е X
th×—
sh ж ch ж ’
c!h х
ch x sh ж
При изменении ж от 0 до оо, sh ж изменяется от 0 до сю, ch х—от 1 до оо, th х—от 0 до 1, cth x—отоо до 1; sh ж, th х и cth ж—функции
нечетные [то есть, например, sh (—ж)=—sh а·], a ch х—функция четная [ch (—2) =ch х]. Основное соотношение:
ch х — sh2 х=1.
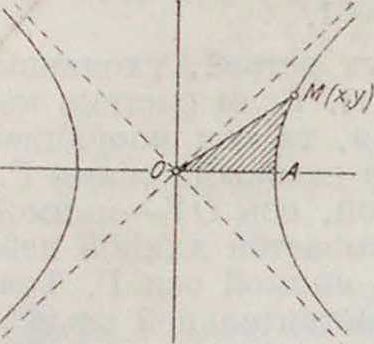
Свое название Г. ф. получили от геометри-ческ. значения. Уравнение равнобочной гиперболы ж2—?/2 — 1 может Сыть представлено в параметрич. форме: х — ch t, у=sh t, где t есть удвоенная площадь сектора МО А (смотрите фигура). Связь гиперболических функ- дий с тригонометрическими функциями (мнимого аргумента): ch х=cos ix, sh x — — i sin ix, где
i=V~ 1.
Если ввести вспомогательный угол φ уравнением th а:=sin ψ, то найдем:
sh®=t.ggp, chx=sec<p.
Ф-лы сложения:
sh (.г + у)=sh x ch у + ch x ch (x -j- y)=ch x ch у + sh ,r Ф-лы дифференцирования:
^=ch», -p-=sh x, dt}x =
dx ’ dx dx
’ dx deth x
dx
Sil y: sh y.
1
eh* x ’
1
sh=.v
Обратные Г. ф. носят названия: ареа синус гиперболический и т. д. (ареа площадь). Выражения этих ф-ий и их производных (через натуральные логарифмы) следующие:
Аг sh х — In (г + /хг + 1);
dArshx 1
dx
V-
(-
Ar ch х=In (x ± V·12 dAr ch x i
I ,v : - 1
oo < x < +od);
- i);
(1 st.r < +oo);
Ar th x =, In
dAr tli x dx
1 - д:3 1
( χ < i);
In
л - 1
Ar cth x=dAr cth x
dx x3
Особенно применимы вытекающие отсюда ф-лы интегрального исчисления, например:
(> 1)·
dx=Ar ch Vx‘ - а»
и т. д. Или при интегрировании с помощью подстановки
I=Г - ·
J <χ*
полагаем х-
7 _ rsh t dt _ e
J sht J
- D*
ch t, тогда dx — sh t dt ; dt. sh* t :
+c.
— cth ί-г C= —
У 1
В технике весьма бЬлыное значение имеет возможность выражать интегралы линейных дифференциальных ур-ий с постоянными коэффициентами при помощи Г. ф от комплексного аргумента. Этот метод позволяет чрезвычайно наглядно изображать соотношения в длинных линиях электропередачи, распределение плотности тока в пазах электрич. машин и т. д. При вычислениях с Г. ф. комплексного аргумента пользуются изображением этих ф-ий в виде:
ch (,т sh (х -
• гу) -
41) =
а -(- гЬ, с -j- id
и применяют таблицы, где приведены значения «, b. с d в ф-ии от х, у; или же изображают Г. ф. в тригонометрическом виде:
ch (х где гу) — се“г, sh (x -f г у)=se·6; th (х -f гу)=(с··,
с=У cos2 у -j- sh2 x; tg y - tg y th x;
tgii tg y cth $; tgr =
Sin 2| sh 2.v
s=J/siii2 y -j- sii2x; t=i.
Существуют таблицы и номограммы, где с у, s, б, I, τ приведены в функции от х, ?/; особенно номограммы Кеннеди удобны для быстрых вычислении с такого рода ф-иями.
Лит.: J ah n k е К. и. К in d с F. Funktionenta-fe.ln mit Formeln u. Kurven, Lpr., 1923: Kennel-1 у A. K., The Application of Hyperbolic Functions to Electrical Engineering Problems, X. Y., 1925; К e n-nelly A. E. Tables of Complex Hyperbolic a. Circular Functions for the Use of Electrical Engineers a. in Mathematics a. Physics, Cambridge, .Mass., 1914: К e η n e 1 1 у A. E. Chart Atlas of Complex Hyperbolic a. Circular Functions, Cambridge. Mass. 1914; C till e n L. Formulae a. Tables for the Calculation of Alternating Current Problems, N. Y., 1913.