> Техника, страница 38 > Гистерезис

Гистерезис

Гистерезис (греческ. ΰατίι>η οις—отставание, запаздывание), физико-химич. явление несовпадения во времени следствия и производящей его причины, несмотря на совпадение их по месту. Действующая причина, вызывающая некоторое изменение в системе, в общем феноменологическом значении есть с и л а, а производимое ей изменение—д е-формация, хотя бы речь шла о явлениях не только механических, но и каких угодно других (электрических, магнитных, коллоидных, химических и т. д.). Гистерезис состоит в том, что деформация системы в каждый данный момент времени соответствует не наличной в этот момент силе, а некоторому прошлому ее значению.

Понятие Г. уясняется, если рассмотреть виды мыслимых деформаций, возникающих в системе при длительном действии сразу примененной постоянной силы F, которая затем сразу же снижается. При этом могут быть деформации: 1)мгновепио возникающие и мгновенно же спадающие; 2) мгновенно возникающие, по вовсе не спадающие, то есть необратимые; 3) постепенно возникающие, по мере действия силы, и постепенно же спадающие, после того как сила снята; это—процессы постепенно обратимые; 4) постепенно возникающие, по мере действия силы, но не спадающие, когда она снята, то есть необратимые. Мгновенные и мгновенно обратимые деформации происходят по типу явлений совершенной упругости, наприм., как она рассматривается в теории упругости твердых тел; точно так же адиабатическое всестороннее сжатие идеального газа, электрич. зарядка газового конденсатора и др. схематически мыслимые процессы относятся к этому виду деформаций. Деформация J)_l тут не зависит от времени г применения силы F. Поэтому эти деформации характеризуются дифференциальным соотношением:

ДО,=1-dF,

2-ч не содержащим времени —модуль упру гости, понимая этот термин в общем феноменологическом смысле). Мгновенные и необратимые деформации происходят по типу явлений хрупкости или а. Зависимость деформации 1)_г от силы /·’ представляется здесь функцией прерывной и потому может быть выражена соотношением уже не дифференциальным, а конечным:

1),

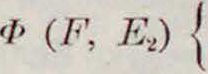
нуль. конеч. величина

ПР» F<F_Kpufn.

где Е₂—характерная постоянная вещества. Постепенные и постепенно же обратимые деформации происходят по типу явлений остаточного последействия. Деформация 1)₃ пропорциональна силе Е и некоторой функции /(г) от длительности приложения (или снятия) силы. Поэтому деформации этого рода характеризуются дифференциальным соотношением:

dD,=p(r) rlr.

где E₃—постоянная вещества, к-рую можно назвать модулем остаточного последействия. Наконец, постепенные и необратимые деформации происходят по тину явлений вязкого трения. Деформация D_i пропорциональна силе F и длительности ее наложения т. Явление характеризуется дифференциальным уравнением:

dD_t=¹ · Fdr,

& «

где Е_а—коэффициент вязкости (мог бы назваться также модулем вязкости).

Действительные деформации, происходящие в природе, обычно имеют смешанный характер и могут быть представляемы как совокупность накладывающихся друг на друга деформаций всех четырех типов. При этом мгновенность l)_t и IK должен быть получаема как протекание процесса в промежуток времени, практически неуловимо малый. Г. обусловлен двумя последними видами деформации. Как последейственнып, так и вязкий Г. весьма распространены в природе в самых различных областях, и м. б. высказано общее положение о подчиненности Г. всех природных процессов. В частности должен быть отмечены мехаиич. деформации твердых тел, электрические и магнитные «смещения» в твердых же средах, явления ионной проводимости в газах (неоновые лампы, вольтова дуга), в жидкостях (электролиты) и твердых телах, фотоэлектрический эффект селена и клеток со щелочными и щелочноземельными металлами, набухание коллоидов, протекание химических реакций, особенно под каталитич. воздействиями, и т. д. Тем не менее Г. изучен плохо, и причиной тому было отсутствие методов, позволяющих подвергнуть эти явления математич. анализу. Лишь применение в 1900 г. интегральных и интегро-дифференциальных уравнений, а в дальнейшем также и «уравнений линий» дало орудие к овладению этими явлениями «с наследственностью».

Явления Г. выступают особенно выпукло, когда сила меняется периодически и запаздывание деформации повторяется, притом весьма часто. В то время как упругая деформация запасает энергию при своем возникновении, а при уменьшении силы отдает ее обратно, вязкая деформация требует при новом направлении силы новой затраты работы, а деформация последейственная, хотя и отдает энергию, но уже противодействующую смыслу новой деформации. Таким образом при периодически меняющейся силе Г. ведет к потерям энергии; отношение этих потерь на Г. w к затраченной мощности W (иногда выражаемое в %) называется коэффициентом мощности Р; Р —. Если вы чертить кривые, связывающие деформацию с вызывающей ее силою, которая меняется периодически, то ветви кривой при прямом и при обратном движении не будут сливаться между собою, когда имеется Г. Таким образом, кривая Г. будет ограничивать некоторую площадь, величина которой есть мера работы, затраченной на Г. Чем совершеннее упругость среды, тем гистерезисная петля уже и в пределе обращается в кривую, симметричную относительно начала координат. Напротив, при полной вязкости среды петля располагается всецело над осью усилий. Вузом выводит следующие законы Г. I. Всякий раз как упругая сила среды достаточна, чтобы установить равновесие с наибольшим напряжением деформирующего усилия, к-рое наложено на нее циклически, площадь полученной петли Г. постоянна, какова бы ни была частота, а рассеянная Г. энергия в единицу времени—пропорциональна частоте. II. Всякий раз как упругая сила среды недостаточна, чтобы дать равновесие с наибольшим напряжением деформирующего усилия, к-рое на среду наложено циклически, площадь полученной кривой гистерезиса меняется с частотою, а рассеянная в единицу времени гистерезисом энергия—не пропорциональна частоте.

Электрический Г. Таблица дает классификацию случаев диэлектрического Г.

Классификация диэлектрического гистерезиса.

Характер изменения электрич. поля	Изменение электрического поля во времени
Внезапное	Резкое наложение или снятие эдс
Непрерыи-	Интенсивность по-
ное	ля есть непрерывная функция вре-
	меня
Периодн-	Интенсивность по-
ческое	ля есть периодическая функция времени (в частном случае синусоидная)

Изменение электрич.! поля в пространстве

Резкий сдвиг диэлектрика в силовом поле или силового поля относительно ди-тектрнка

Д иэ л с кт р ик движется в поле или ноле! движется в диэлектрике

Диэлектрик перио-j дически движется г. поле или иоле периодически движется в диэлектрике (в части, случае—вращается).

Практика встречается чаще всего с периодическим изменением поля во времени. Если на конденсатор с твердым диэлектриком наложена некоторая эдс V, то упругая электрич. деформация выражается емкостным током I, хрупкая электрич. деформация—током пробоя /о, последейственная—аномальным обратимым током 1₃ и, наконец, вязкая—током проводимости /₄. Ток 1₃ пропорционален емкостному 7, но убывает со временем г: h=β С ν·ψ(τ),

где β—постоянная вещества, С—емкость конденсатора, а убывающая функция времени φ(τ) одинакова для всех веществ. Различными соображениями вид этой функции устанавливается так:

(г)= bг-^т

φ (г)=ае~ъ-^п

^φ^=ϊΤ^ *(^Γ>“ΤΤΤ+^β

(Кольрауш, Гопкннсон, Гизе,Ж. Кюри, Швейдлер, Иордан, Гранье и др.), (Ж. Кюри),

(Ж. Кюри, Швейдлер, Вильсон),

(Троутон и Ресс);

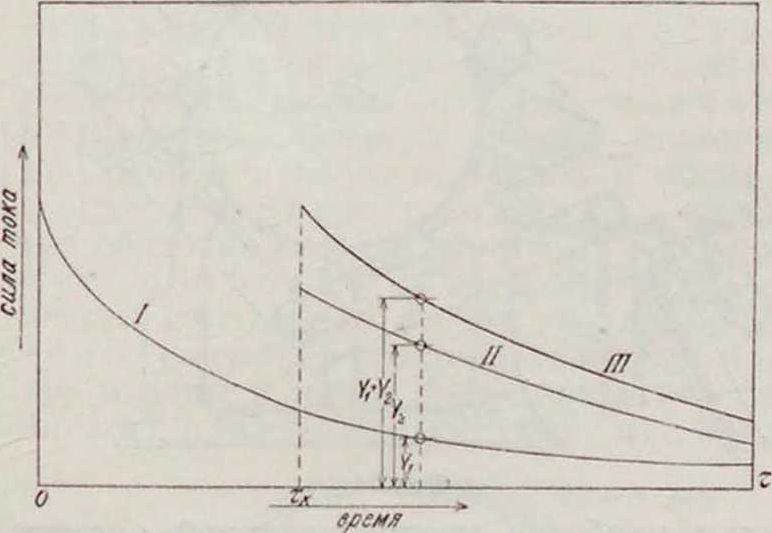
а, Ь, с т, п означают характерные постоянные вещества. Эти соотношения в пределах точности измерений приблизительно одинаково оправдываются наблюдениями. Аномальный ток 1₃ подчиняется закону су-перпозиции, или наложения (Дж. Гоп-кинсоп и Ж. Кюри). Этот закон состоит в независимости друг от друга действий разных причин, вызывающих аномальные токи. Иначе говоря, если на рассматриваемый конденсатор наложено последовательно несколько эдс в разные времена, то суммарный аномальный ток будет в каждый момент времени алгебраич. суммою токов, вызываемых каждою из эдс порознь и протекающих так, как если бы других эдс не было. Диаграмма (фигура 1) поясняет этот закон: кривая показывает течение аномального тока ?/, кривая II—тока у₂, если бы он возник самостоятельно, в момент г_ь а кривая III показывает течение совокупного аномального тока, который в каждый момент равен у₂ + у₂.

Таким образом, если в последовательные моменты г_к (к=1, 2, 3,., п) накладываются соответственные эдс Δ* V, то аномальный ток в момент г будет:

I,=fiC%A_tV.p( τ-τύ,

1

а при непрерывном изменении электродвижущей силы

h=βΟ f ^d dl^U> · <Р (^τ - м) Au,

где и есть тоже время, но не текущее время т, а время, от которого зависит изменение эдс. При этих нее условиях ток проводимости будет:

Л=*· V(z),

а ток емкости:

где *—коэфф-т электропроводности, a е.— диэлектрический. Что же касается тока пробоя /₂, то мы предполагаем его равным нулю. Такова одна из схем поведения диэлектрика в электрическ. поле. Из нее, далее, выводится поведение диэлектрика в поле периодическом, когда V=TVsin ²у^гУ, где Т—период. Частный случай—когда считаются с Г. только вязким. Тогда полный ток слагается из тока емкости, выраженного косинусоидою, и тока проводимости, выраженного синусоидою, причем периоды их равны Г, а амплитуды различны. Это равносильно смещению г

Фигура 1.

фазы полного тока в отношении напряжения на угол <1, называемый углом диэлектрических потерь, причем

1 т

2 π Т

Величина

1 ε

4гс х

tg ό -

Τ

носит название релаксац и и; tg ό равен коэффициенту мощности: tg Д=Г. Работа сил поля за один цикл

Л_т —

vl с т т

то есть пропорциональна квадрату максимальной эдс, пропорциональна длительности цикла и обратно пропорциональна релаксации. Амплитуды тока смещения и тока проводимости характеризуются след, величинами:

М=С Ко (амплитуда тока смещения) и

У=^iK*- · С · V₀ (амплитуда тока проводимости). Цикл диэлектрич. вязкого Г. при синусоидном напряжении представляет эллипс. На фигуре 2 показано семейство таких эллипсов

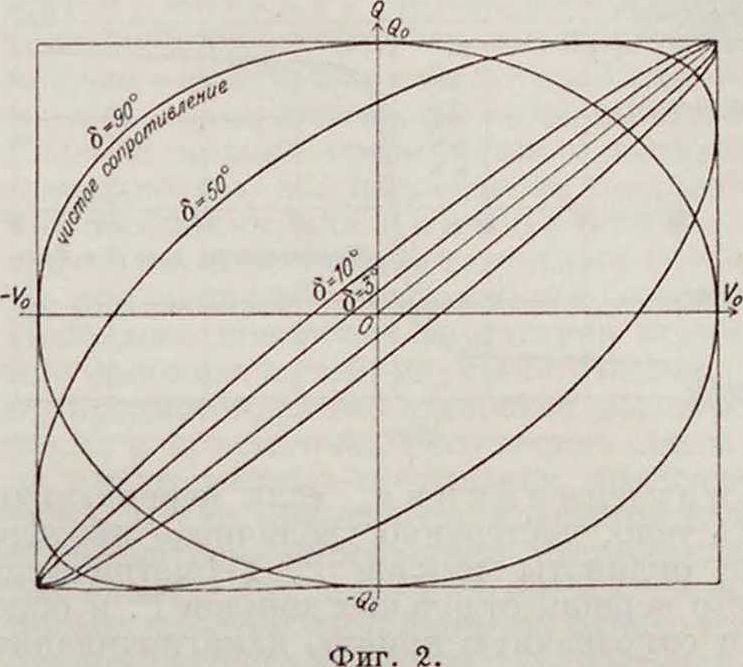
для различных значений S, причем на оси абсцисс отложены эдс (изменяющиеся циклически), а на оси ординат—соответственные заряды конденсатора. См. Диэлектрики, Волокнистые изоляционные материалы, Изоляционные материалы.

Лит.: Б я л о С р ж е с и и ii Ч. Ф., Ионизация жидких и твердых диэлектриков, «Университетские известия.!, Киев, 1912, 5.9; Флореиси и и П. А., Диэлектрики и их техническое применение, ч. I, М., 1924 (здесь же библиография); Lahousse, «RUE», 1924, t. 15, Ιό. ρ. 62, 16, ρ. 667 (с, библиография); Schweidler Ё., «Ann. d. Physik», Lpz., 1907, B. 24, p. 711; Wagner К. W., «KTZ», 1911. Η. VII, p. 172, 1913, II. XLV, p. 1279; Wagner К. W., «Ann. d. Physik», Lpz. 1913, B. 40, p. 817; W a g n e r K. W., «Arctiiv i. Elektroteclmik», 1914, B. 2, 3. p. 371; Bouzon R. «RGK», 1919, t. 6, 5. p. 137—148. «, p. 181—187; Handhucli derElektri-zitat und des Magnetismus, hrsg. v. L. Graetz, В. 1, I,pz., 1918. П. Флоренский. г’нстерезис ферромагнитных тел заключается в том, что магнитная индукция В в данной точке тела зависит не только от одновременного значения напряженности магнитного поля Я в этой точке, но также и от предшествовавших состояний тела, от его «истории». Т. о., в ферромагнитных телах индукция В является многозначной и весьма неопределенной функцией напряженности поля Н. В технике особенно часто встречается периодич. перемагничива-ние, когда Я и В периодически изменяются между крайними значениями. На фигуре 3 изображены две крив ы е, или петли, Г., изображающие зависимость между В и Я, когда В периодич. изменяется между В_тахи В_тЫ (при чем В_тЫ=-В_тйх). Сплошная кривая соответствует отожженному электролитическому железу, пунктирная кривая—листовой динамной стали. Каждому значению Я соответствуют 2 значения В—в восходящей и в нисходящей части петли Г. При периодическом перемагничивании кривая симметрична относительно оси абсцисс.

Когда 11=0, В обладает некоторым конечным значением. Эта ордината начала называется остаточной (ремане нтной) индукцией. Для того чтобы индукция обратилась в нуль, необходимо наличие некоторого от-рнцательн. поля И. Этот отрезок абсциссы до встреч» с кривой Г. называется коэрцитивной (задерживающей) силой.

Форма петли Г. зависит от обработки тела, от его t° и даже от толщины (скин-эффект). Можно однозначно определить кривую

20000

/0000

/0000

20000

		*3 II
			у“,·
		F; ^ “,	1
5ΰ 2	0	о · Ί	! /. //аорт	0 2 енност	0 поля /$	о 4? о 4/см
		J
?

Фиг. н а м а г и и ч и в а н и я, если перемагничи-вать тело, постепенно увеличивая предель-пые ординаты циклов I. Геометрическое место вершин отдельных циклов Г. и образует однозначную кривую намагничивания.

Каждое изменение магнитного состояния тела вызывает выделение теплоты, как бы медленно ни происходило это перемагничи-вание. При замкнутом цикле перемагничи-вания теплота Г_н, выделяющаяся в единице объёма, определяется по формуле V_H =jHdH.

⁰

Если измерять 11 в А/см, ai?в вольт-ск./с.и²=10⁸ гаусс, то V_H будет измерено в джоулях на ем³. Так. обр. площадь петли Г. служит мерой затраты энергии, теряемой при одном цикле перемагничивания. На практике было бы слишком сложно для определения потерь каждый раз планиметрировать петлю Г., и потому пользуются приближенными ф-ламн. Штейнмец дал эмпирич. ф-лу:

Vff — η-f-B¹’* эрг/с.м³ в ск.,

^ΓΊ max г где f—частота, »/—постоянная, зависящая от материала. Эмпирич. коэфф. Г. η зависит от выбора предельной индукции. При В_тах==10 000 гаусс, коэфф-т Г. η для дииамной стали=0,0013—0,0015, а для трансформа-торнон стали s 0,0006—0,00075. В настоящее время применяются значительно ббль-шие индукции, при которых потери на Г. возрастают пропорционально 2-й или даже 2,2-й степени индукции, так что ψ-ла Штейн-меца становится неприменимой.

Рихтер предложил для В до 16 000 гаусс формулу:

100

Rrnax г о

i ооо ¹

1 (1>тпЛ-100 1 ООО ) ^ ¹

Для листовой динамной стали, толщиной 0,5 лш, а и ji, вычисленные по этой формуле, имеют следующие значения:

а β

Для обычной дииамной стали. 0,9 з.а

Для стали с больш. примесью кремния 0,4 2.в

То же для толщины листон в о,35 .«.и. 0,3 2Л

Для больших индукций можно с достаточной точностью пользоваться более простой формулой:

^Гя=‘дЦ₁₍У² W/кг.

Здесь для обыкновен. динами, стали ε=4,4, а для стали с большой примесью кремния ь - 2,4—3,0, в зависимости от толщины листа.

Возможность применения этих ф-л для очень больших индукций, порядка 23 000 гаусс, сомнительна, так как для таких индукций потери на Г. еще мало исследованы. Мало исследован также Г. вращения, когда вектор индукции, сохраняя свою абсолютную величину, меняет свое направление. Чистый Г. вращения весьма трудно наблюдать, так как в большинстве случаев (наир., в якорях динамомашин) меняются и абсолютная величина и направление вектора В. Произведенные исследования заставляют предполагать, что потери на Г. вращения сначала возрастают вместе с индукцией (приблизительно до 1C 000 гаусс), а затем, при дальнейшем увеличении индукции, сильно уменьшаются и уже при В =24 ООО гаусс достигают ничтожно малой величины.

Лит.: Ш р а м к о η Е. Г., Производство электро-технич. листового железа в России. «Техи.-экон. вестник», Москва, 1924, 2, стр. 169; Епифанов Н. О., Производство электротехнического железа на Верхне-Исетевом заводе, «Электричество», Москва, 1926. 7, ггр. 318: Richter R., Elektrische Masehinen, Berlin. 1924: G » m 1 i c h E., Leitfaden der magneti-sehen Messungen. Braunschweig. 1918: Spooner T. Properties and Testing of Magnetic Materials, New York, 1927. Я. Шпильрейн.