> Техника, страница 38 > Годограф скорости

Годограф скорости

Годограф скорости. Пусть точка перемещается по некоторой траектории АВ. В каждый момент времени вектор скорости v направлен по касательной к траектории в со ответствующем положении точки, причем v —, где»·—радиус-вектор,определяющий положение точки на кривой по отношению к некоторой системе отсчета с произвольным началом U (фигура 1). Вектор ускорения а равен производной вектора v по времени ί

(смотрите Двиэ1сеиие) а~ Если от некоторой про извольной точки О, откладывать векторы h=v, то, при перемещении точки по своей траектории, вектор

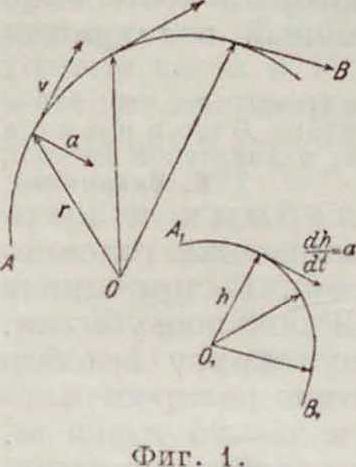
/дет менять в оо-щем как свою абсолютную величину,так и направление, имея одно и

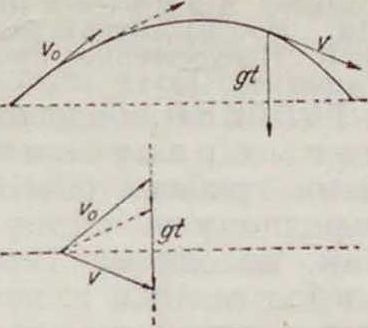
Фигура 2.

то же начало 0₁. Конец вектора ft будет описывать кривую, называемую годографом скорости. Так как вектор h для кривой А₁В₁играет ту же роль, что вектор г для кривой АВ, то скорость коночной точки вектора h, при ее перемещении но А_гВ_г, равна

dh dn г,-,

_dt=_dj=a. Таким обр., видно, что вектор ускорения точки, движущейся по некоторой траектории, равняется в каждый момент соответствующему вектору скорости конца вектора, описывающего Г. с. Плоскость, касательная к Г. с. и проходящая через ft, будет, очевидно, параллельна плоскости, проходящей через а и v, то есть она будет параллельна соприкасающейся плоскости кривой АВ. При прямолинейном равномерном движении (v — Const) Г. с. стягивается в одну точку Если точка перемещается по кривой, имея одну и ту же линейную скорость (υ= Const), то Г. с. представляет собою кривую, описанную на шаровой поверхности радиуса v. При плоском движении, Г. с.—плоская кривая. Для свободной материальной точки, брошенной под углом к горизонту с некоторой начальной скоростью v₀, имеем: v=v„ + f/t, где v—вектор скорости точки по истечении времени f, а г=Const—вектор ускорения силы тяжести. Так как ft„== t»₀=Const, а вектор <)t сохраняет постоянно вертикальное направление, то конец вектора h=v постоянно лежит на вертикали, то есть Г. с. для рассматриваемого слу чая представляет собою вертикальную прямую (фигура 2). Если точка описывает конич. сечение с постоянною секториальною скоростью (смотрите Двиэюение) относительно фокуса конич. сечения, то Г. с. представляет собою окружность. Г. с. впервые был рассмотрен Гамильтоном, а затем Мёбиусом.

Лит.: С у с л о в Г., Основы аналитическ. механики, т.1,ч. I—Кинематика, Киев, 1911; MObiusA., Element? d. Mechanik d. Ilimmels, Lpz., 1843; H a-m 1 1 t ο n V., Elements of Quaternions, London, 1846; G e r 1 a c h 0., /.ur Theorie d. Hodographen, Rostock, 1889; A 1 t H., Zur Theorie der (Jeschwindigkeits-und Bescbleunigungsplane einer komplan bewegten Ebene. Dresden, 1914; M e h m k e it., Zur graphi-schen Kinematik u. Dynamik, Jabrbuch der deutscben Mathematiker-Vereinigung, Halle a/S., p. 561, 1903; Hame 1 G., Elementare Mechanik, 2 Aull., Lpz. 1922; Wittenbauer F., Graphlsche Dynamik, Berlin, 1923. M. Серебренников.