> Техника, страница 40 > Графическое интегрирование

Графическое интегрирование

Графическое интегрирование. В случае, когда требуется найти интеграл F (Х)=

Т

J Д.г) (1.т и для fix) дан график, вместо а вычисления F(X) для разных значений _Х(смотрите Вычисления прибли-женные) гораздо проще построить график функции F(X), который позволит с достаточной точностью находить значения этой ф-ии для различных значений аргумента (смотрите фигура). Для кривой у—fiх)

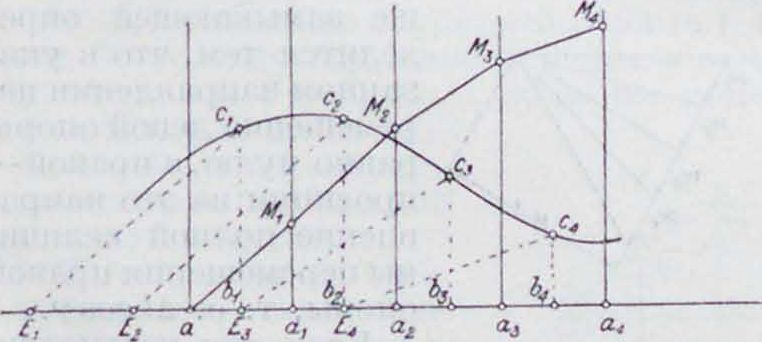
строим ординаты в точках соответствующих абсциссам а, α₁=α+Α, a₃=a + 2h, а₃==α+3/ι,., а также (пунктиром) проводим ординаты в серединах этих промежутков, Ь₁=а+, Ь, =а + ~, Ь₃=а + ^. Затем выбираем единицу масштаба для площадей— отрезок Z—и откладываем его влево от точек by, b_t, Ь₃,. до точек Еу, Е_г, Е₃,. (на фигура I 2h). Соединяем (пунктиром) Еу с вершиной Су ординаты точки by и из а проводим прямую параллельно ЕуСу до пересечения в точке Му с ординатой, соответствующей а,. Отрезок аМу изображает приблизительно течение интегральной кривой между а и a + h. Далее, соединяем Е₃ с е₂и проводим

МуМо и Е_гс_г до пересечения с ординатой при а₂; проводим прямую Е₃с₃ и параллельно ей отрезок М_гМ₃, и т. д. Все течение кривой y=F(X) приблизительно изобразится ломаной аМуМ_гМ₃. В самом деле, по формуле трапеций (смотрите Вычисления приближенные) имеем: F(h) os (у о + у у)·, из подобия треугольников аауМу и Е.ЬуСу следует: — ^b,c.

аа_х Е_ХЬ_Х

Но Eyby=1, ЬуСу=^Vo“-^!-, aay — h, следовательно, dyMy=(у₀ + у у) os F(h). Точно так же моясно доказать, что

α,Μ, == ζ (i/o + У у) + § (Уу + у₂) =

2 h

Qi I f(x)dx=F(2h).

J

0

Лит.: Крылов А., Лепцпи о приближенных вычислениях, СПБ, 1911. В. Степанов.