> Техника, страница 40 > Графическое определение перемещений

Графическое определение перемещений

Графическое определение перемещений. Графнческ. способам отдают предпочтение, когда требуется определить перемещения целого ряда точек, например, прогибы всех узлов фермы. В отдельных случаях и для нахождения перемещения одной точки графические приемы могут дать наиболее простое, а иногда и единственное решение, именно, когда аналитич. решение сопряжено с интегрированием сложно интегрируемых или неннтегрируемых ф-ий. Г. о. п. применяется как для систем сплошных (балки, арки, рамы), так и для систем шарнирно-стержневых (фермы). И в том и в другом случае предполагается, как это вообще принято в теории сооружений, что перемещения являются величинами весьма малыми по сравнению с общими размерами тела; поэтому для тел гибких (проволока, кабель и т. и.) излагаемые ниже приемы неприменимы.

Построение перемещений в сплошных системах. В сплошных системах пренебрегают влиянием продольной и поперечной силы на деформации и строят перемещения, учитывая только изгибающий момент. Из теории известно выражение кривизны изгиба: ~=— щ, где М— изгибающий момент в сечении, Е—модуль упругости первого рода, 1—момент инерции

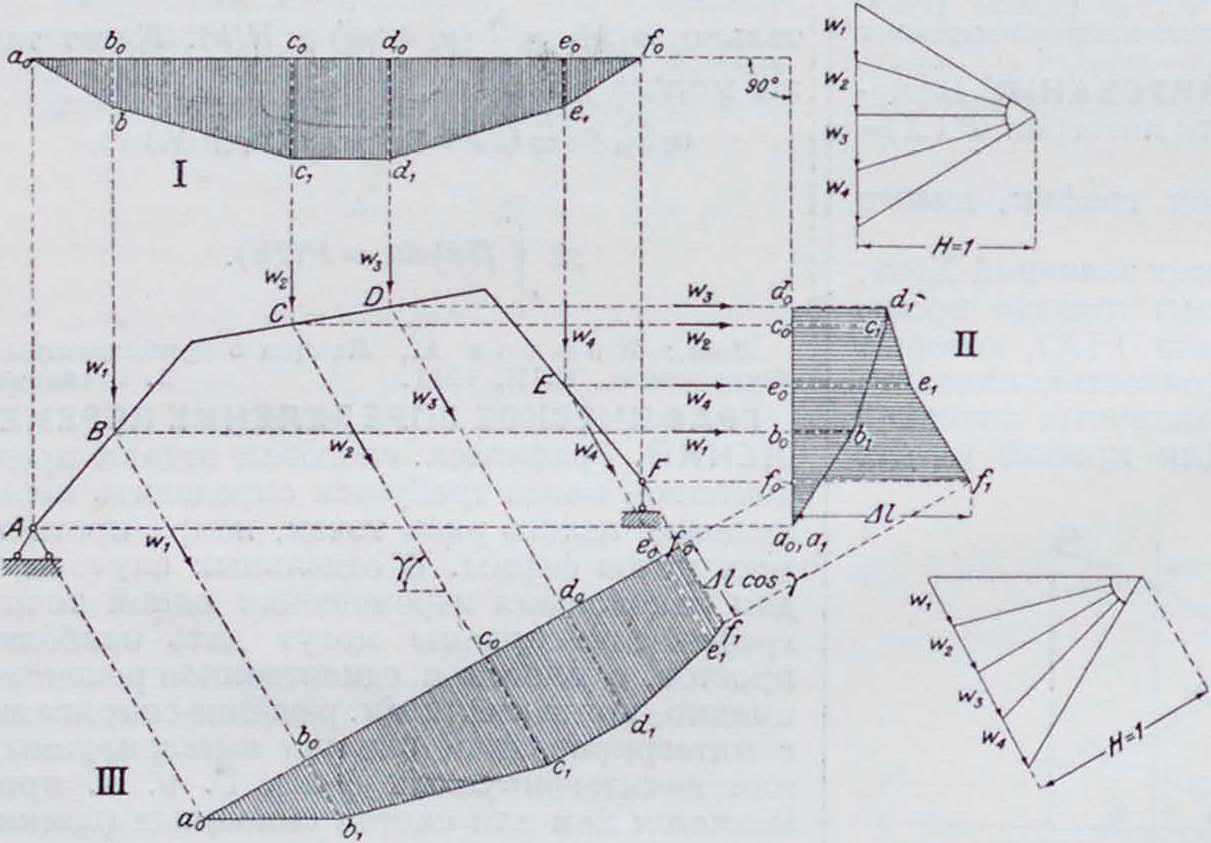
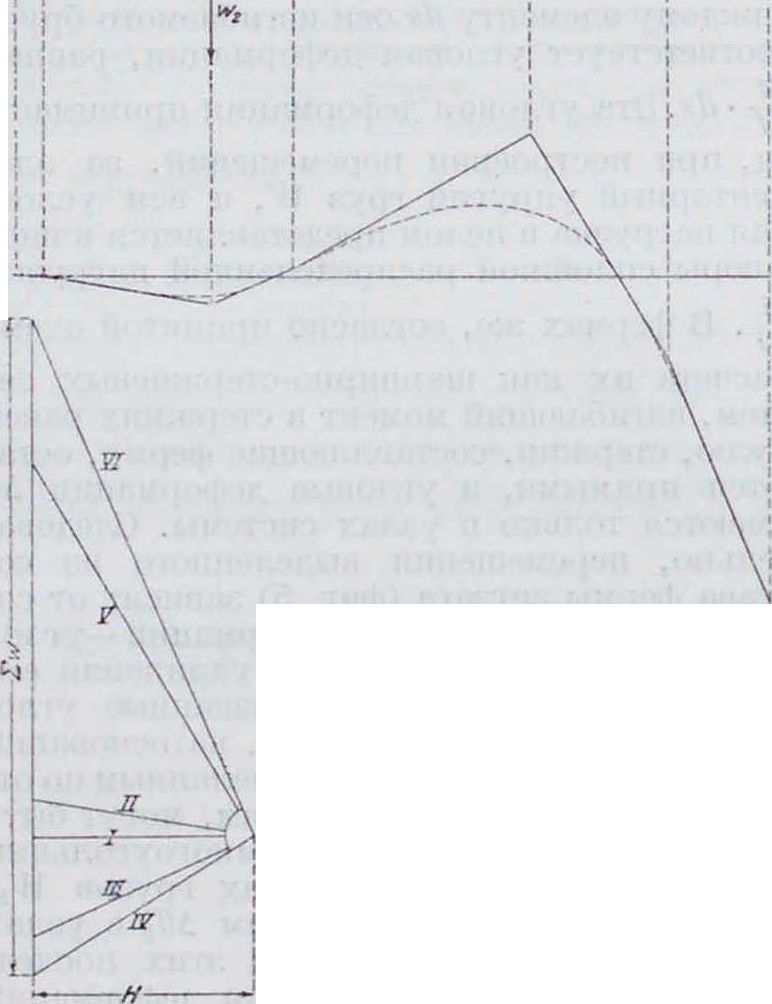
влении (III). При построении перемещений в направлении, перпендикулярном плоскости качения подвижной опоры, замыкающая определяется тем, что в упругой линии точки, соответствующие опорам, не имеют в искомом направлении перемещений, следовательно, замыкающей будет прямая, соединяющая точки, полученные путем снесения на веревочную кривую опор."При определении перемещений в направлении подвижности правой опоры, то есть в направлении, перпендикулярном предыдущему, замыкающая определяется из условия, что перемещение неподвижной опоры А равно нулю, а поворот сечения бруса на этой опоре, то есть угол наклона первого луча веревочного м-ка к замыкающей, равен углу поворота, определенному построением (I). Исходя из этих соображений, построение перемещений в этом направлении ведут след, образом: упругие грузы W направляют параллельно направлению подвижности правой опоры и строят для них веревочный мн-к, стороны которого проводятся в направлении, перпендикулярном соответствующим сторонам мн-ка (I). Затем через точку я₀. которая соответствует неподвижной опоре А, проводят замыкающую под углом в 90° к замыкающей мн-ка в построении (I). Отрезки относительно этой замыкающей, б₀·^, c_u-C₁,. будут равны перемещениям точекЛ,В,С,., аотрез-ком М — f₀-f₁ определится величина перемещения подвижной опоры F. Для нахождения перемещений в косом направлении условные силы W ведут параллельно этому направлению и строят веревочный мн-к при том же полюсном расстоянии II,. как и в построениях (I) и (II). Положение же замыкающей определится тем, что в указанном направлении перемещение левой опоры равно нулю, а правой— проекции на это направление полной величины перемещения правой опоры, то есть Mcosy.

Если для рассматриваемой системы момент инерции является величиной постоянной, то величина условной нагрузки го=прямо пропорциональна ординатам эпюры М. И этом случае за нагрузку можно принять площадь эпюры моментов, но так как упругие грузы в этом случае увеличатся в EI раз, то для получения перемещений по-прежнему в масштабе чертежа надо и полюсное расстояние взять соответственно увеличенным в EI раз.

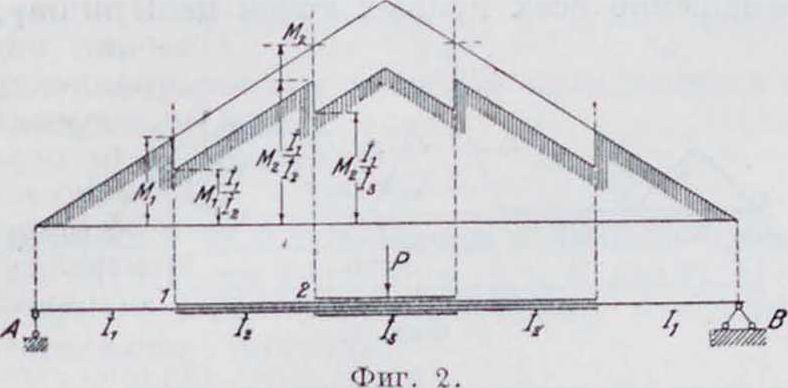
Если сечение балки изменяется так(фигура2), что в отдельных участках (1-м, 2-м, 3-м и т. д.) моменты инерции 1_г, 1₃ остаются постоянными, то за условную нагрузку целесообразно принять значения нагрузок,

Фигура 1.

заменяют равными им по величине сосредоточенными силами 1 Г, приложенными в ц.т. этих площадей. Затем эти условные силы W сносят на ось бруса, направляют их параллельно искомым перемещениям и строят для них веревочную кривую при полюсном расстоянии, равном единице в масштабе силового многоугольника. Ординаты построенной таким образом упругой линии измеряются относительно некоторой замыкающей, способы построения которой видны из следующего примера (фигура 1), в котором для бруса ломаного очертания построены перемещения в трех направлениях: перпендикулярно плоскости подвижности опоры (I), параллельно этой плоскости (II) и в косом напра-

сечепия и ()—радиус кривизны, для которого дифференциальная геометрия дает ур-ие: i _ у _#^е [i +

Пренебрегая в знаменателе величиной О/)² в виду ее малости по сравнению с единицей, получаем дифференциальное выражение упругой линии в следующем виде:

Из сопоставления этого ур-ия с ур-ием веревочной кривой (смотрите Веревочный многоугольник) Ну"= —с, где Н—полюсное расстояние, у—ордината кривой и г—ордината эпюры распределений нагрузки, заключаем, что упругая линия может быть построена как веревочная кривая, при условии, что за нагрузку будет взята условная распределеи-м“

нал нагрузка w — -gj, а полюсное расстояние II будет принято равным единице. Построение это вполне аналогично построению эпюры моментов от действительной нагрузки и производится след, образ. За нагрузку принимают эпюру значений го — и делят на возможно большее число частей. Площади каждой такой части, равные ^· As,

М, Г Μ, _r Μ,

равных, i₀, Ι₀, и τ. д., а полюс-

ное расстояние II взять равным 1 Е/₀, где У₀—произвольно взятое значение момента инерции (на фигура 2 принято /„=/!). В предыдущем изложении предполагалось, что перемещения должен быть построены в масштабе чертежа, но т. к. перемещения — величины

весьма малые, то практически их приходится строить в значительно увеличенном масштабе. Для чертежа, построенного в масштабе натуральной величины и при требуемом увеличении перемещений в т раз против натуральной величины, общее увеличение перемещений против масштаба чертежа будет в тк раз, что достигается путем уменьшения во столько же раз полюсного расстояния, то есть, в том случае, когда за условную нагрузку принята эпюра моментов, полюсное расстояние II принимается

Изложенные приемы применимы и для построения перемещений в кривых стержнях (брусьях малой кривизны) в тех случаях, когда возможно пренебречь влиянием на деформации нормальной и поперечной сил (смотрите Арки). Пример такого построения горизонтальных и вертикальных перемещений для кривого бруса переменного сечения дан на фигуре 3. За упругие грузы в этом построении взяты величины Μ ^Ι° As, а полюсное расстояние II принято равным 1 -Е1₀, где М—среднее значение момента в данном участке As, I — среднее значение момента инерции для этого участка и /„—нек-рый произвольно выбранный момент инерции.

Построение п е-р е м е щ е н и и нет а-тически неопре-д елимых системах. После того как найдены лишние неизвестные и построена эпюра моментов, построение перемещений в статически неопределимых системах не отличается от такового для систем статически определимых. На фигуре 4 показано построение прогибов для неразрезной балки постоянного сечения, заделанной на левом конце и с консолью на правом. За условную нагрузку принята эпюра моментов, построенная при помощи фокусных то чек (смотрите Балки перазрезпые)·, полюс выбран так, чтобы первый луч был горизонтальным; направление этого луча будет служить замыкающей, так как ось бруса в месте заделки остается горизонтальной. Построенная упругая линия пересечет эту замыкающую под всеми опорными точками.

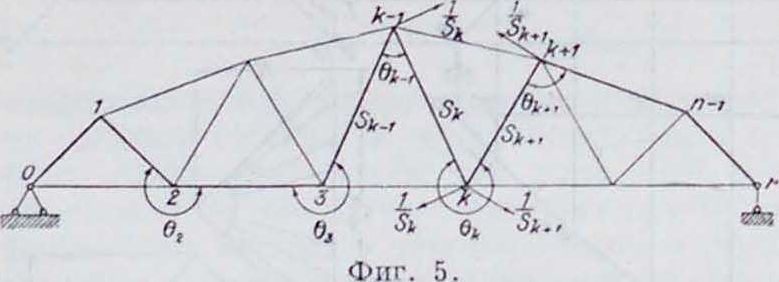
Перемещения в фермах. Для нахождения перемещений в фермах выделяют из состава фермы непрерывный шарнирностержневой зигзаг, проходящий через опоры и через те узлы, перемещения которых требуется определить (фигура 5). Образования прогибов в фермах отличаются от таковых в системах сплошных тем, что в последних каждому элементу (Is оси изгибаемого бруса соответствует угловая деформация, равная

_;‘у · сIs. Эта угловая деформация принимается, при построении перемещений, за элементарный упругий груз W, а вся условная нагрузка в целом представляется в виде эпюры сплошной распределенной нагрузки

j.j-. В фермах же, согласно принятой схеме расчета их как шарнирно-стержневых систем, изгибающий момент в стержнях равен нулю, стержни, составляющие ферму, остаются прямыми, и угловые деформации АО имеются только в узлах системы. Следовательно, перемещения выделенного из состава фермы зигзага (фигура 5) зависят от сосредоточенных угловых деформаций—углов О между его сторонами и от удлинений его сторон S. Перемещения, вызванные угловыми деформациями в узлах, на основании рассуждений, аналогичных сделанным по отношению к сплошным системам, могут быть построены, как веревочный многоугольник для сосредоточенных упругих грузов П₄, равных угловым деформациям А0_к в узлах шарнирной цепи. Величины этих последних определяются из условия деформации всей фермы; способы определения их указаны ниже. Перемещения, получающиеся в зигзаге шарнирной цепи в результате удлинения ее сторон, м. б. также получены при помощи веревочного мн-ка путем выражения

Фигура з. их через упругие грузы И. Действительно, перемещения, вызываемые удлинением какого-нибудь стержня S_k на величину AS*., могут быть представлены как сумма двух

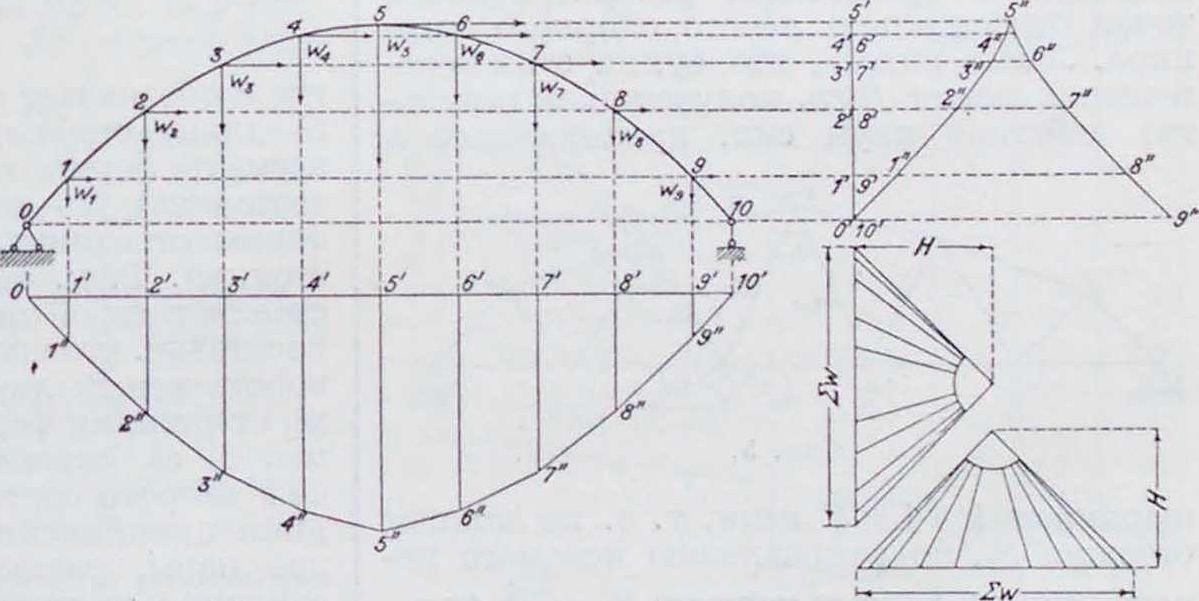
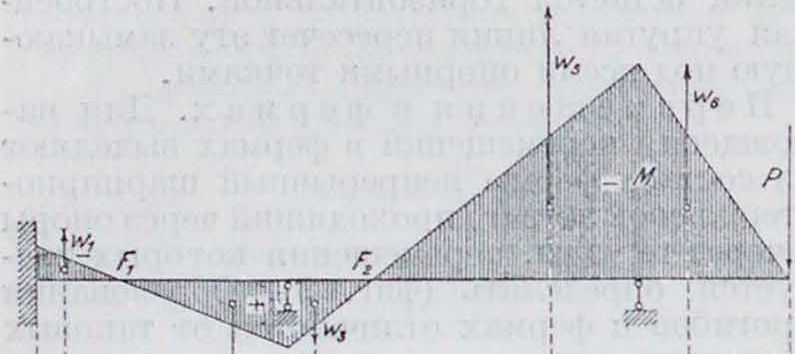
перемещений (фигура 6): 1) перемещения любой точки зигзага правее узла к на величину AS_k, в результате чего правый концевой шарнир цепи сместится также на величину AS_k,

Фигура 4.

и 2) перемещений всех точек цепи как жесткого целого до совмещения правого концевого узла с направлением плоскости подвижности. Первое из этих перемещений по рассматриваемому направлению для всех правых точек определяется величиной AS_k sin а_к. Второе для всех точек цепи опре деляется формулой: ΔΘ-х=^1α*·х, где

А0„—поворот цепи вокруг левого опорного шарнира; х—расстояние рассматриваемой точки относительно левого опорного шарнира. Легко видеть, что сумма этих перемещений может быть получена как результат действия пары сил, приложенных к

шарнирам /с —1 и к цепи, то есть по концам стержня S_k, по направлению искомого перемещения и равных каждая: W=· tg а“.

Момент этой пары:

-tga* · S_k-cos a_k=AS_k · sin a_k,

T. e. равен перемещению всех правых точек цени. Вызываемая же ее действием фик тивная опорная реакция на левом конце --J—~ΑΘ₀, τ. е. равна углу поворота цепи как одного жесткого целого вокруг левого шарнира. Выбор направления сил пары делается в зависимости от вида перемещения, вызываемого удлинением AS_k стороны S_k. Если это удлинение вызывает перемещение всех правых точек цепи книзу,

кг

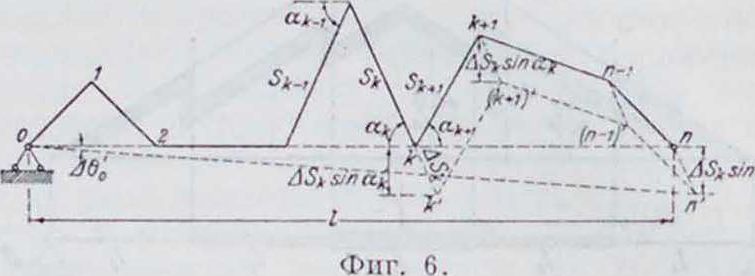
то паре дается направление положительного момента, то есть но ходу часовой стрелки; если лее все удлинение таково, что смещение правых точек происходит кверху, то паре сил дается направление, вращающее против хода часовой стрелки. Т. о., упругий груз II в узле к при пололштельном значении углов а и удлинении сторон S_k и S_kkl, будет определяться выражением вида:

W_k=А0_к tg а_к +. tg а_к+1.

Первый член правой части учитывает влияние на перемещение угловой деформации А0_к шарнирной цепи, а второй и третий— влияние линейных деформаций сторон зигзага. Если стержни зигзага горизонтальны, то тангенсы углов наклона стержня к горизонту обращаются в нуль, второй и третий член в выражении упругого груза пропадают, и вычисление упругого груза упрощается. Первый член выражения упругого груза, то есть угловую деформацию АО, можно подсчитать или исходя из аналитич. приемов определения деформаций или из. геометрии. соображений. Первый способ, наиболее общий и пригодный для любой фермы, заключается в нахождении углового перемещения по следующей формуле (Мора)

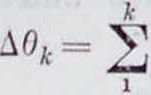
ΛΓ· N Е · (о

S,

где οι обозначает площадь сечения стержня, S—длину стержня, N—значение усилия в элементе фермы от данной нагрузки (первое состояние), N—значение усилия в элементе фермы от единичной нагрузки второго состояния. Т. к. искомое перемещение представляет собой от-

носителыь угол по- -

ворота между дву- 4

мл стержнями фер- --У·

мы, то за систему г

СИЛ второго COCTO-яния принимаются ^А

две пары, равные Фигура 7.

единице, противоположные но знаку, приложенные к этим стержням S_k и S_k+_V Следовательно, величины

i i.

этих сил соответственно равны ^ и ; направление их берется таковым, чтобы угол получал положительное приращение.

Если ферма состоит из простых тр-ков, то приращение любого угла тр-ка легко определяется но следующим ф-лам (фигура 7). Для определения деформации угла тр-ка 0_а прикладываем к сторонам его S_h и по паре с силами ‘ и J. Тогда усилия от этих пар

&1> & с в сторонах тр-ка иудут:

/V

* ’ а

К=- ~ · cos 0_b; Ν„=- 1_а · cos 0,

Т. о., деформация угла 0„ представится в следующем виде:

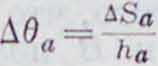
Λ&7

К

cos 0_Ь -

AS*

h_a

• cos 0_С.

Заменяя в этом выражении величины h„ через равшлс им величины h_a=& sin 0_Ь h_a== 8_b sin 0/, 8„=h„ (ctg 0_С + ctg 0*) и сделав приведение, получим:

г, Δ8 JV П

1ак как относит, удлинение _s-=-_у— =-_{,.,

где п—нормальное напряжение, то предыдущее равенство м. б. выражено так:

Е АО,=(п_а - п_е) ctg О* + (п_а - π*) ctg 0_С. Вообще же, если угол О, образуемый шарнирной цепью, слагается из нескольких

Фигура 8.

углов тр-ков, входящих в состав фермы, то величина упругого груза W_k, зависящего от деформации АО, м. б. вычислена по ф-ле:

]Г,=АО,=^ £[(»„-«,) ctg О* +

+ («в - ^пь) ctg 0,]·

Если производится вычисление упругих грузов W в зависимости от угловых деформаций АО цепи и удлинений AS стержней цепи, то есть по формуле:

И*= АО, - tgа“ + ig±i tg «ж,

то при этом учете парам сил, определяющим 2-е состояние загружения, надо дать направление искомого перемещения (фигура 8), то есть приложить к сторонам цепи пары с силами

± ₌ ._¹____н _±_ ₌ _1__

d_k SjCOSa* dk-t-I St+iCOSCi/fc-f!

Эти силы, будучи разложены по направлениям, перпендикулярным к стержням цепи, и по направлению стержней цепи, приведутся: 1) к парам с силами g¹- и g~, определяющим влияние деформации угла АО, на величину упругого груза и 2) к продольным силам: -_s! tga, и tga,₊₁, определяющим влияние деформаций сторон AS* и AS,₊₁ на величину упругого груза. Переходя к напряжениям, можно пользоваться следующим выражением для упругого груза ТУ,: EW_k=Е АО, ± M,_, tg α,_ι, ± Ящ tg a, ,₊₁.

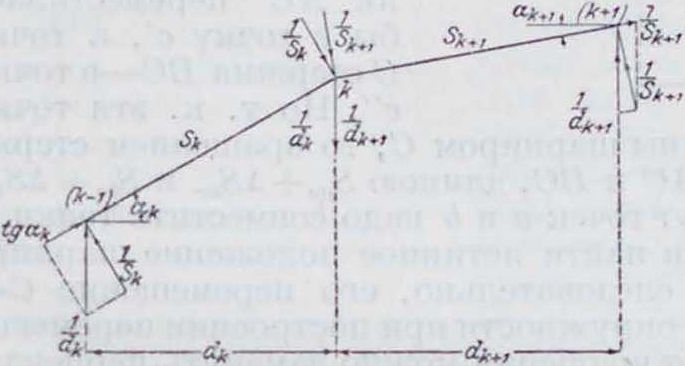
Для примера последовательности построения па фигура 9 показано построение прогибов нижнего пояса консольной фермы. В виду того, что все элементы зигзага горизонтальны, второй и третий члены в выражении упругих грузов отпадают. Чтобы получить прогибы, увеличенные в к раз против натуральной величины при масштабе чертежа в _п,

полюсное расстояние взято равным Н =

(в масштабе упругих грузов). На построенный для упругих грузов веревочный мн-к снесены опорные точки и проведена замыкающая прямая, относительно которой измеряются прогибы узлов системы. Иногда для упрощения расчетов упругие грузы W вычисляют только по деформациям поясов, то есть пренебрегая деформацией решетки. Этот прием, однако, влечет за собой довольно значительную погрешность в конечных величинах прогибов. Графическое определение м. б. также применено для построения горизонтальных составляющих перемещений узлов, подобно тому как это было показано для сплошных систем. К такому построению приходится, наир., прибегать при нахождении перемещения в трехшарпирных арках (фигура 1U). В этих системах нельзя непосредственно определить искажение угла в шарнире S арки по выведенным выше ф-лам; нахождение его делается на основании следующих соображений. Горизонтальное перемещение правой опоры, равное нулю, вследствие неподвижности обеих опор арки, м. б. рассматриваемо как сумма двух перемещений: 1) перемещения в результате искажения всех углов, кроме угла в шарнире S, и удлинения всех сторон зигзага и 2) перемещения в результате искажения угла в

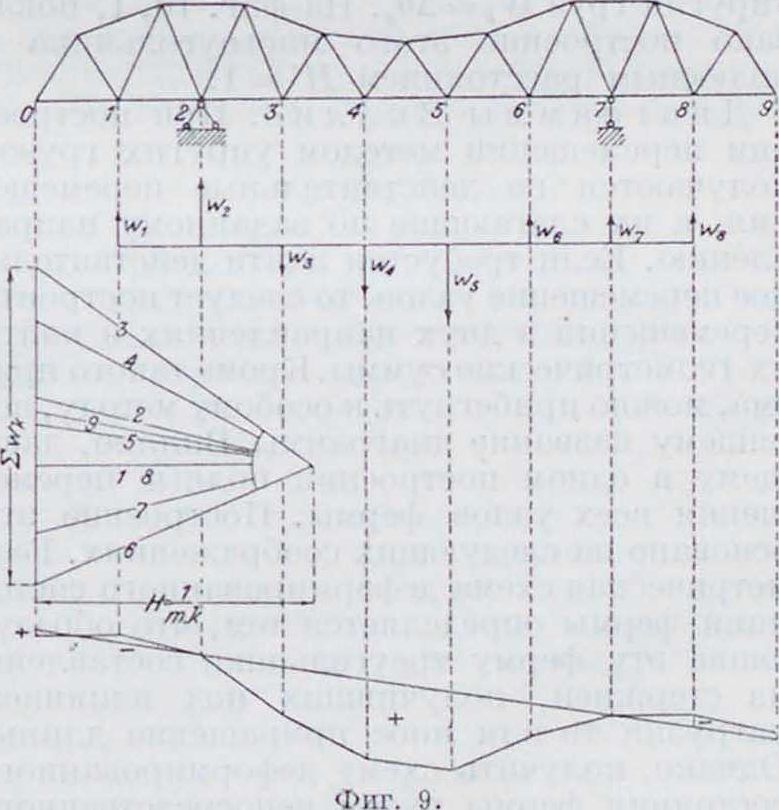
шарнире. Обозначая первое из этих перемещений через А/, получим Αί + · A0_S=0, где /—расстояние шарнира S от линии перемещений. Величина перемещения М слагается, как указано выше, из перемещения

АГ, вызываемого деформациями углов АО цепи, и перемещения АГ, вызываемого деформациями AS стержней цепи. Первое из них может оыть веревочного зонтального определено путем построения мн-ка (фигура 10, II) для гори-направления упругих грузов

45

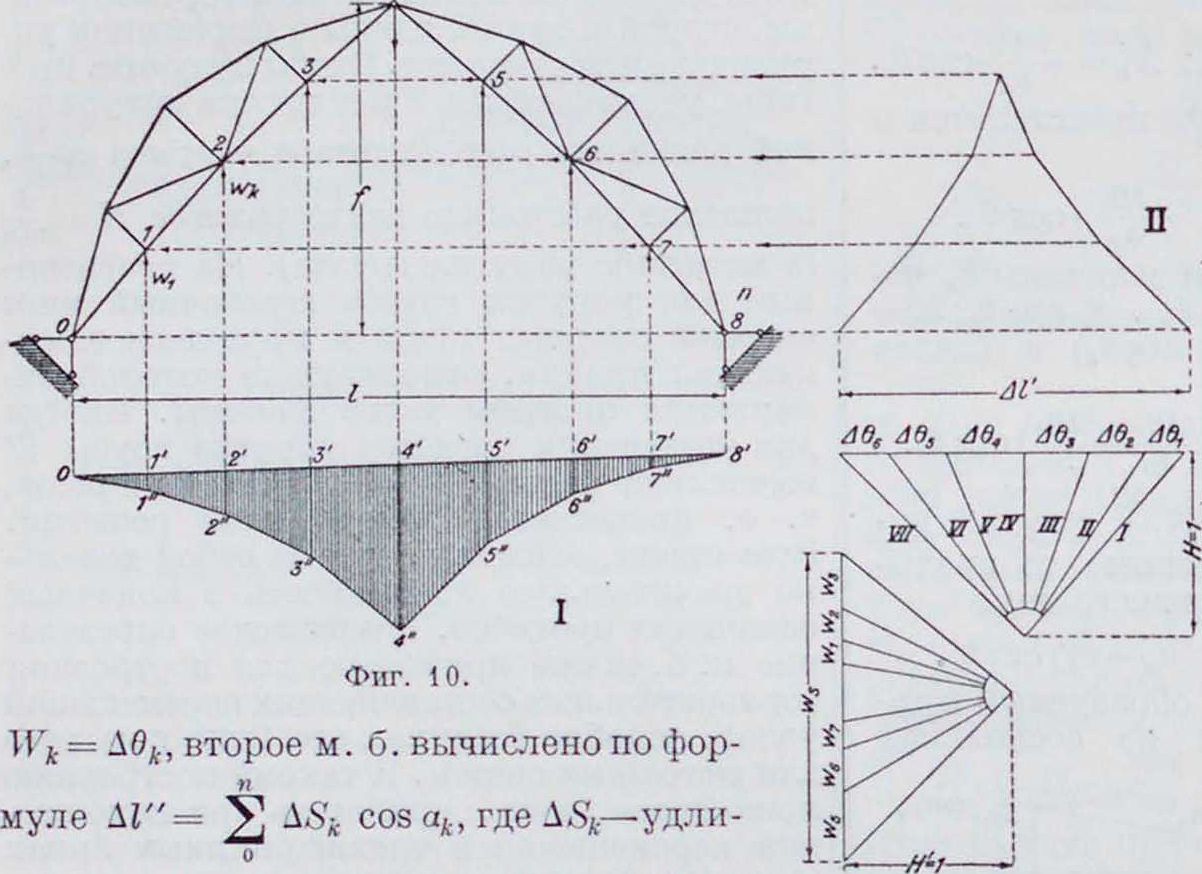
некие стороны цепи, а а“— угол наклона ее к линии перемещения. Таким образом, для определения абсолютной величины деформации угла при шарнире S мы будем иметь:

АО,=у (АГ + 2 AS* cos а“)·

Когда определена величина АО, построение линии прогиба арочной фермы делается путем построения веревочного мн-ка для упругих грузов 1Г=А0, включая в число их и упругий груз !Г,=А0,. На фигуре 10, I, показано построение этого многоугольника с полюсным расстоянием Я=1.

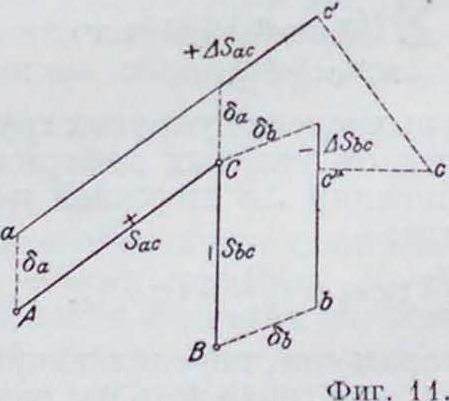
Диаграммы В и л л и о. При построении перемещений методом упругих грузов получаются не действительные перемещения, а их слагающие по заданному направлению. Если требуется найти действительное перемещение узлов, то следует построить перемещения в двух направлениях и найти их геометрические суммы.Кроме такого приема, можно прибегнуть к особому методу, носящему название диаграммы Виллно, дающему в одном построении полные перемещения всех узлов фермы. Построение это основано на следующих соображениях. Геометрическая схема деформированного состояния фермы определяется тем, что образующие эту ферму треугольники составлены из стержней, получивших под влиянием нагрузки то или иное приращение длины. Однако, получить схему деформированного состояния фермы путем непосредственного геометрия, построения тр-ков по их деформированным сторонам практически нельзя, т. к. приращения длин стержней—величины весьма малые, в масштабе фермы выражающиеся ничтожными отрезками, и, следовательно, точность такого построения была бы весьма малой. Взамен этого в диаграмме Виллно приращения длин и перемещения узлов строятся на особом чертеже отдельно от чертежа фермы и в значительно увеличенном масштабе. Построение это основано на следующих соображениях. Предположим (фигура 11), что мы имеем шарнир С, связанный стержнями АС и ВС с шарнирами А и В. Требуется найти перемещение <5_С шарнира С в результате того, что шарниры А и В получили перемещения ύ_α и д₆, равные A-а и Β-ίι, а стержни АС и ВС получили приращения длины, равные AS„_C и - AS₆₍. Если бы рассматриваемые стержни не были связаны с шарниром С и перемещались параллельно самим себе, то в результате перемещений шарниров А и В и удлинений стержней Л С и ВС точка С стержня АС переместилась бы в точку с а точка С стержня ВС—в точку с". Но т. к. эти точки С, то вращением стерж-

Т AS„. и — AiSj

связаны шарниром ней АС и ВС, длиною S_aвокруг точек а и b надо совместить точки с и с" и найти истинное положение шарнира с и, следовательно, его перемещение С-с. Дуги окружности при построении перемещений от вращения можно заменять перпендикулярами к радиусам вращения, в виду того что приращения AS,, и AS_br—величины весьма малые по сравнению с длинами S,« и S_bc. Само же построение можно отделить от чертежа стержней и сделать в стороне.

Sa

-"ΊΓ la*

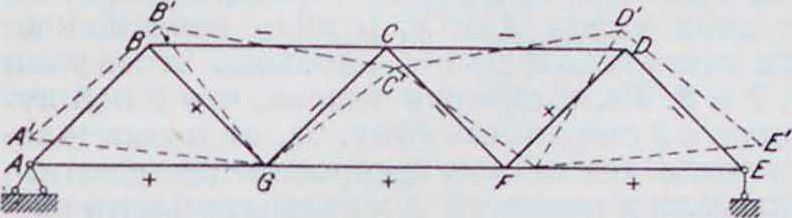
Пользуясь этим приемом, построение диаграммы Виллио ведут в следующем порядке (фигура 12). Предварительно подсчитывают приращение длин стержней под влиянием усилий в них и температурных изменений по формуле:

bS_k=£*.S_k + a-t.S_k,

где N_k—усилие в элементе к, <«*—сечение элемента, S*—длина элемента, I—приращение темп-ры и а—коэфф. расширения. Затем, чтобы диаграмма получилась более компактной, предполагают первоначально, что один из узлов, ближайших к средине, папр., узел С/, неподвижен, а направление одного из элементов, выходящих из этого узла,

например элемента 67<’, предполагают постоянным. Затем строим перемещение точки /<’, откладывая отрезок AS_gf—gf параллельно GF. Зная теперь перемещение точки G, принятое равным нулю, и точки /<’, равное gf, строим перемещение точки С, для чего из f откладываем отрезок AiSy„, равный и параллельный приращению длины стержня FC, и из точки //отрезок A.Sp,., равный и параллельный приращению длины стержня GC- Из концов этих отрезков восстанавливаем перпендикуляры, точка пересечения которых с определит отрезок дс, равный по величине и

с направлению перемещению точки С. Имея те-перьна диаграмме точки, соответствующие перемещениям точек С и F, строим перемещение точки D, и т. д. При этом окажется, что благодаря сделанному нами предположению о неподвижности узла G и направления стержня GFопори, точки А и Е сместятся с опор и займут положение А и Е. Чтобы совместить эти узлы с опорами, надо дать всей ферме поступательное движение до совмещения точек А и А и вращательное движение до совмещения точки Е с плоскостью подвижности правой опоры. Истинные перемещения узлов при этом окажутся равными геометрической сумме перемещений, найденных в предположении неподвижности узла (7, и перемещений от поступательного и вращательного движений фермы в целом. Эти геометрические суммы можно построить следующим образом. Из точки спроводим прямую, параллельную направлению возможного перемещения узла Е, т.е. горизонтальную прямую, и из точки и проводим прямую, перпендикулярную этой прямой; точку пересечения этих двух прямых обозначаем через е". На отрезке ае" строим фигуру, подобную чертежу фермы, но повернутую на 90", и обозначаем узлы теми же буквами, что и на чертеже фермы, по с двумя значками. Отрезки между двумя одинаковыми бук

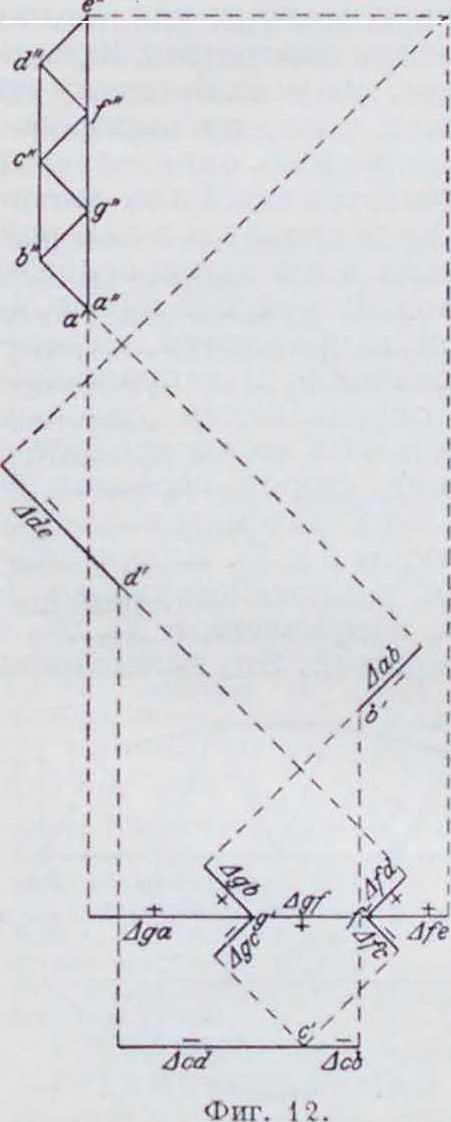
вами и будут равны по величине и направлению действительным перемещениям соответствующих узлов, причем направление этого перемещения будет от точки с двойным значком к точке с одиночным значком. Построение Виллио, обладая тем преимуществом, что сразу в одном построении получаются полные перемещения узлов, все же сравнительно реже применяется в русской практике, чем метод упругих грузов. Объясняется это тем, что в этом способе неизбежно накопление чертежных ошибок и результаты могут получиться с значительными погрешностями. Во Франции, однако, применяют преимущественно диаграмму Виллио.

Лит.: Прок о ф ь е в И. П. Теория сооружений, ч. 3, Москва, 1928; Сими некий Р. К., Строительная механика, ч. 2, Киев, 1927; Тимошенко С. П., Курс статики сооружений, ч. 1. изд. 2, Л., 1 926; М ю л л е р-Б р е с л а у Г. Графпч. статика сооружений, т. 2, пер. с нем., СПБ, 19 10—13; Μ 0 1 1 е г-В re s 1 a u Н., Die Grafische Stalik d. Baukonstruktionen. В. 1, Leipzig. 1922: Piri et J., Kompendium d. Statik d. Baukonstruktionen. B. 2, T. i. Berlin. 1921; Land. Kinematische Theorie d. Statik bestimmt. Triger, «Ztschr. d. Oesterr. Ing,- u. Archit.-Ver.», Wien, 1888, p. 11. 162; Μ о h r. Bei-trag z. Theorie d. Fachwerks, «Zeitschrift. d. Archit.-u. Ing.-Ver. zu Hannover». 1875. p. 605; W i 1 1 i о t, Notations pratiques sur la statique graphique. Publicat. scientif. industrielles. P. 1877. H. Щапов.