Греффе способ

Греффе способ вычисления корней ал-гебраич. ур-ий основан на следующих рассуждениях. Пусть ур-ие я-й степени имеет действительные и неравные по абсолютной величине корни; строим последовательно ур-ия, корнями которых будут 2-е, 4-е, 8-е и т. д. степени корней первоначального уравнения; в полученныхт. о. последовательных уравнениях наименьший по абсолютной величине корень будет представлять все меньшую часть предыдущего. Если полученное после достаточного ряда таких преобразований уравнение имеет вид х” + ЬуЛ*-¹ + М*"* + · + Ь„ _ ,х + b „=О

и его корпи (все положительные) в убывающем порядке суть х, > х,. > х„, то из ф-лы Х_г + Х_{г +}. +х_п= -Ь, имеем: х₁^—Ь₁,т. к. все последующие слагаемые малы сравнительно с первым; далее, по той же причине х,-х_ае“Ь_а, χ₁·χ_ί·χ₃s— b₃, ., откуда

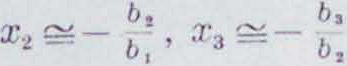
Извлекая из найденных значений х, х₂- ·· .,х„ корень соответствующей степени, найдем корни заданного ур-ия.

Построение уравнения, корни которого суть квадраты данного, ведется в след, порядке. Пусть и (х)—левая часть данного ур-ия: д (х)=х^п + а₁х^п~¹ + а.л^м~~^г 4- ··· +

+ α„_ιΧ + α„. (1)

Строим выражение

(-1 )^пд(-х)~х^п-а₁х^п-· + citX"-- -. 4-+ (-1)” - ^ια„ _ iX + (-1 )"а„. (2)

Произведение выражений (1) и (2) состоит из множителей (х — х,) · (х + х,·)=х^г — х, где г 1, 2,.п. Заменяя в произведении х² через г и приравнивая нулю, получаем искомое уравнение и-й степени относительно г с корнями х, Щ,., х“. Коэффициенты нового ур-ия вычисляются по схеме:

	а“	а,.
— а,	а,	— а“.
-а?		— а»
+2а,	-2а,а,	+2а,а₄
	+ 2а,	-2а,а₆ +2а.
ь,	ь,	Ь,.

Суммы столбцов 1, Ь₁,Ь₂, Ь₃,. суть коэффи-циенты нового ур-ия. Так как число цифр в коэфф-тах при повторении очень быстро возрастает, то (ведя, наир., вычисления при помощи логарифмич. таблиц) округляем результаты, оставляя одну цифру до запятой, число значащих цифр, даваемое таблицей, и

1-я ГТЧНОНЬ.	8	10	2 1
1	-64	100	-4
	+ 20	- 32
З-Я ». 1	-44	+ 08	- 4
1	-1,(13(1-10*	4,024-10*	- 1.0-10*
	+0,131·.· ш“	-0,352-10*
4-Я “. 1	-1.S00-10*	4,272-10*	- 1,6-10
1	-3,240· 10*	1,823·10*	-2.56-10*
	0,00».10*	-0,004-10*
S-Я ». 1	-3,231-10*	1,81»·10	-2,56-10*

умножаем на соответственную степень 10 (так, в данном ниже примере вместо 1 930

берем 1,9 36 -10³). После нескольких раз применения описанного процесса удвоен, произведения будут исчезающе малы сравнительно с квадратами; тогда останавливаем процесс, вычисляем корни последнего ур-ия по вышеприведенным формулам, извлекаем корень соответственной степени и получаем абсолютные величины корней исходного уравнения; знак этих корней определится подстановкой в ур-ие.

Пример в и числения. Дано уравнение x-f8x²+ 10x4-2 0. Для вычисления его корней находим коэффициенты новых ур-ий по схеме (А): останавливаемся на 8-ой степени, далее удвоенные произведения не окажут влияния па 4-ю цифру. Корпи исходи, ур-ия будут равны по абсолютной величине:

[х,|=УЗДЗМО⁶ =6,512;|х.,|=-ί/Ι ^м ‘

= 1,241; |х₃|=^{г ьй} ·0,2476.

’ ^{1 31} У 1.819 - 10’

Т. к. данное ур-ие не может иметь положительных корней, то перед всеми значениями надо взять знак—; контроль: сумма корней дает —8,0006 —8,0000.

Случай мнимых корней представляет некоторые затруднения;например, если входит одна пара мнимых сопряженных корней, занимающая по модулю 2-е и 3-е место, так что х£=д (cos φ 4- i sin φ) x_a=g (cos φ — i sin ψ), то после, например, преобразования, примененною к 8-м степеням, получим:

то есть модуль мнимого корня определен; для определения ψ воспользуемся равенством: х, -(- 2д cos <р + x_t + .= — а_г.

Если мнимых корней более одной пары, расчет еще более затрудняется. При всем том метод Греффе практически должен быть признан лучшим способом приближенного разыскания корней алгебраических ур-ий.

Лит.: М л о д з с е в с к и ii Б., Решение численных уравнении, Москва, 1024: К р ы л о в А. Лекции о приближенных вычислениях. СПБ, 1911: It unge С. и. К. б n i g Н., Vorlesungen uber numerisehes llecb-nen, Gruntiloliren d. mathem. Wissensch. usw. B. 11. Berlin, 1924. В. Степанов.