Группа

Группа, понятие, введенное в математику в 111 веке и получившее, особенно за последнее время, широкое применение в различных ер областях.

Рассмотрим в качестве примера Г. нерест а и о в о к. 11 усть дано конечное число элементов, наир., цифр: 1,2,3. Известно, что из этих цифр можно сделать 3!=6 различных перестановок, а именно 123, 231, 312, 132, 321. 213. Перейдем от перестановки 123, которую считаем начальной, к перестановке 312. Переход состоит в том, что цифру 1 заменяем 3, 2— 1 и 3—2; эту замену назовем о и е р а ц и е и и обозначим символом (jijj). При помоши этой же операции можем перейти от перестановки 21:1 к перестановке 132, от перестановки 321 к 213 и т. д. Т. о., символы (д.¹^), (Jjifj, обозначают не разные, а одну и ту нее операцию, тогда как (Щ) и Г,’;?,)—символы разных операций. Операция ({J.J, оставляющая все цифры без изменения, называется т о ж д е с т в о и и о и операцией. Всегоимеем различных операций (1, аименно:

GS). (Ж). ® (IS)· (Ж). (S)· <’>

Пусть мы хотим перейти от перестановки 123 к 231, а затем от перестановки 231 к 321. Для этого сначала производим операцию

(^2з), затем (Щ). Но операция (:ig}) тождественна с операцией (jijij) ряда. Поэтому производим последовательно операции (^), (]:jg). В результате получим операцию ((ig). т. к. 1 при первой операции перешла в 2, а 2 при второй операции в 3, и т. д. Последовательное проведение двух операций нашего ряда (1) называется умножением опе раций, а результат — произведе и ие м. Легко проверить, что произведение двух любых операций ряда (1) дает снова некоторую операцию того же ряда. Другими словами, вместо перехода от одной перестановки ко второй, а от второй к век-рой третьей существует непосредственный переход от первой перестановки к третьей. Совокупность операций, содержащих тождественную операцию и таких, что произведение двух операций совокупности дает операцию той же совокупности, называется г р у и и о й. Итак, О операций ряда (1) образуют Г. (перестановок из 3 элементов). В арифметике и элементарной алгебре произведение не меняется от перемены мест сомножителей: 3-2= =2-3=6. При умножении операций этот закон переместительности не всегда выполнен, то есть результат зависит от порядка множителей, папр.:

[г31 /132 _ /321. /1324 /231Ч _ /213

123 (1231 ~ 12.1 > (123 1123 J ^— (l23 *

Г., в которых закон переместительности операций выполнен, называются переместительными, или абелевыми, Г.

Г. перестановок—пример Г. конечного порядка, то есть содержащей конечное число операций. Г. конечного порядка играют большую роль в высшей алгебре в вопросе о решении ур-ий высших степеней. Эта теория разработана фрапц. математиком Галуа. Особенно важную роль играют в этой теории абелевы I’. Кроме Г. конечного порядка, существуют Г. бесконечн ы е, то есть состоящие из бесконечного числа операций. Наиболее существенным классом таких Г. являются Г. непрерывн ы х п ре-о б р а з о в а и и й. Предположим, что некоторое твердое тело движется по плоскости, переходя из положения Л в положение В, а затем из положения В в положение С. Ясно, что два перемещения из А в В и из В в Г можно заменить одним перемещением из Л в С непосредственно. Т. о. движения твердого тела образуют группу, ибо два перемещения (операции), произведен, подряд (умножение операций), можно заменить одним перемещением (операцией той же совокупности). Кроме того, если тело остается в покое, то мы имеем тождественную операцию. Так как положений твердого тела на плоскости бесчисленное множество, то группа содержит бесконечное множество операций.

Выразим перемещения в аналитич. форме. Свяжем с начальным положением тела прямоугольную систему координат XOY (смотрите фигура). При перемещении тела в новое положение система координат перейдет в ХОУ. Перемещение тела характеризуется т. о. перемещением системы координат,следовательно, аналитически преобразования Г. движений можно толковать, как преобразования координат. Эти последние даются формулами: 2,=:rcoR φ + у sin φ + я; у =xsin ψ У cos φ+b (величины а, Ь и φ указаны на чертеже). Т. к. a. b п ч могут изменяться непрерывно,

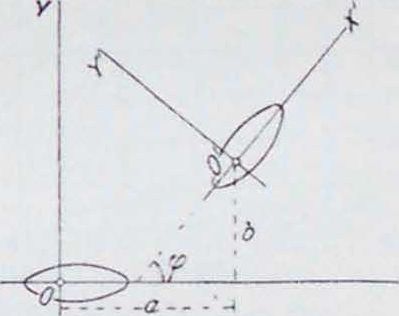
то получается непрерывная Г. преобразовании. зависящая от трех параметров а, b и φ. Общую теорию Г. непрерывных преобразовании развил шведский математик Софус Ли. Теория бесконечных Г., в частности теория непрерывных Г., имеет приложения в геометрии и дифференциальных ур-инх.

Лит.: Граве Д. Теории конечных групп, Киев. 1908; его же, Курс алгебраического анализа. Киев. 1910; Klein 1·. Vorlesungen ilber hOhere Geometrie, Berlin, 1926; L i e S. Vorlesungen uber Differentialgleichungen mit bekannten iniinitesimalen Transformationen, bearb. u. lirsg. v. G. Scheffers, Leipzig, 1891. В. Степанов.