Гука шарнир

Гука шарнир, один из видов четырехшарнирного сферич. механизма, применяется для передачи вращения от одного вала к Другому в том случае, когда оси валов пересекаются и угол между ними не является величиной постоянной. Четырехшарнирный сферич. механизм обладает тем основным свойством, что оси всех четырех вращательных пар его А, В, С и 1) пересекаются в одной точке О (фигура 1). Соединив элементы этих пар стержнями а, Ь, с и d, получим шарнирную четырехзвенную систему АВС1). Поставленная на одно из своих звеньев, эта система дает четырехшарнирный пространственный механизм, все движения которого можно рассматривать как определенные вращения систем углов АОВ. ВОС и АОЛ. Форма и вид стержней никакого значения не имеют, т. к. от звена требуется лишь жесткость соединения соответствующих элементов двух соседних пар; поэтому для удобства исследования за стержни принимают дуги, которые получаются от пересечения плоскостями углов АОВ, ВОС, АОЛ и СОЛ поверхности шара, описанного из центра О радиусом, равным единице. Если звену А В придать форму жесткого угла

Фигура 1. Фигура 2.

АОВ, то механизм получит вид, изображенный на фигуре 2; очевидно, что при движении звена АЛ с угловой скоростью <«, звено ВС будет перемещаться с той угловой скоростью ω₂, как и в случае основного механизма (фигура 1). Продолжив стороны жесткого угла АОВ по другую сторону вершины его О и дополняя механизм, изображенный на фигура 2, механизмом ему симметричным относительно центра О, получим механизм (фигура 3), в котором угол АОВ превращен в жесткий крест АВОВ Ά и оси вращения каждой пары симметричных звеньев расположены по прямой, проходящей через центр О. Вращение звена А Л с угловой скоростью <«,

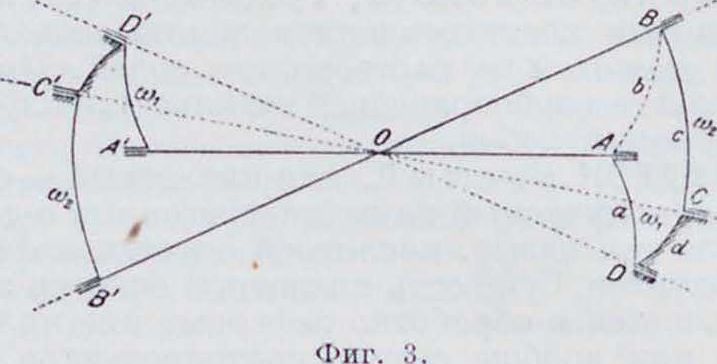
вызывает вращение симметричного ему звена АЛ с той же угловой скоростью «и,; так как обе стороны креста АО и О А вращаются с той же угловой скоростью ω, около осп ЛЛ, то звено АЛ можно выкинуть, закрепив втулку пары А на продолженном звене А Л (фигура 4); по тем же соображениям звено ВС, вращающееся с угловой скоростью ω,. можно исключить, укрепив втулку пары В

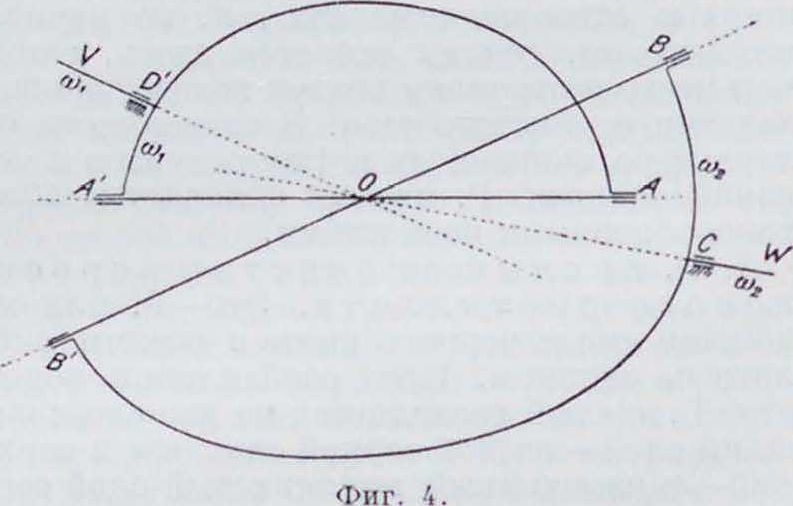
на продолжении звена ВС (фигура 4); полученный таким обр. механизм ААВВСЛ ест:, о б о б щ е н н ы и шарнир Гу к а.

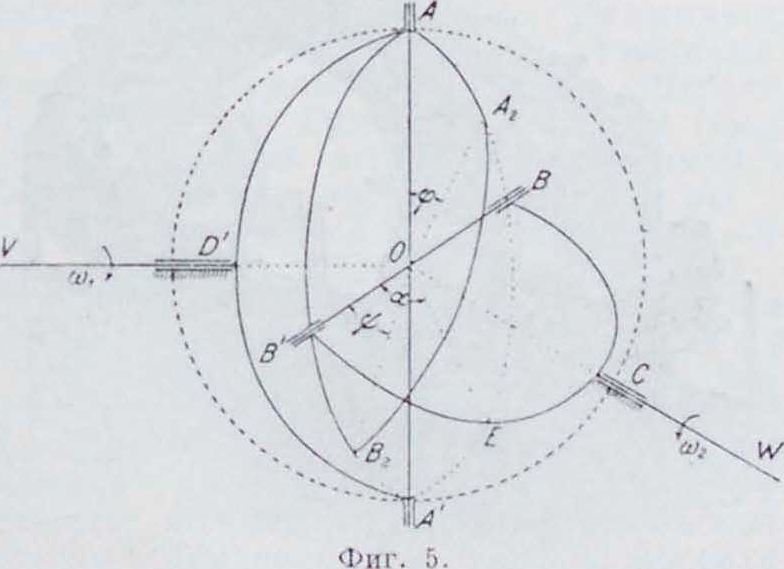
В машиностроении нашел применение тот частный вид Г. щ., в к-ром углы АОЛ, АОВ и ВОС являются прямыми (фигура 5); этот механизм носит название Г. ш., или к а р д а-новой м у ф т ы, и состоит из крестообразной муфты ААВВ, перекладины которой жестко соединены под прямым углом, и двух вилок ВСВп А ЛΆ, закрепленных па концах соответствующих валов; вилки имеют на своих концах втулки для шипов муфты (крестовины). При вращении вала Vконец А звена ЛА будет перемещаться по дуге АЕА окружности большого круга, перпендикулярного к оси УЛО, конец В звена ВС будет перемещаться по дуге АВ Ά окружности большого круга, перпендикулярного к оси 1ГСО. Для определения зависимости между угловыми скоростями <«, и ω₂ валов V и ΙΓ примем за начальное положение механизма то, когда поперечина А А крестовины перпендикулярна к плоскости осей валов FOII. При вращении вала Г с угловой скоростью ω, радиус ОА переместится за время г в положение ОА₂; вал II, вращаясь с угловой

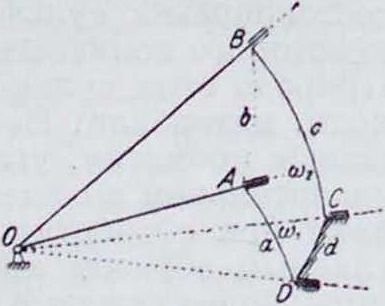
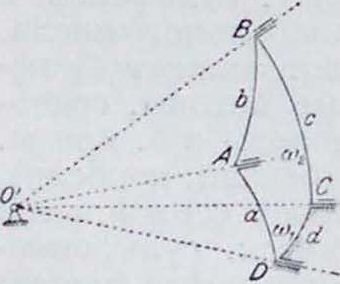
скоростью ω₂, переместит за то же время τ конец вилки B в точку В_г, следовательно:

<01 =

Л;

<а„

Н di

(1)

Дуга ЛГГ заняла положение А ₂Й₂, стягивая прямой угол А_гОВ, дуга Л А ₂ большого круга ЛЕА стягивает угол ΛΟΛ₂=φ, а дуга ЛВ_г стягивает угол ^40Β₂=90°+ψ. На основании зависимости в сферич. треугольнике cos α= cos i)·cos с + sin Ь· sin с-cos А

можно определить зависимость между углами φ и ψ нашего сферич. тр-ка ДД₂В₂(фигура5). Полагая

АВ_г=с — ~ + ψ; АА,_=Ь — <р; А_гВ_г=α= ^ ; А—а,

получим:

COS *=COS φ COS

(:+«)+

Sill φ · Sin

in(” + V’)

COS a,

что после преобразовании дает: tgtp=tg<p-cosa; дифференцируя по t, получим:

	1 dy_	i dy
	cosV di	t-os-v dt
то есть	1	1
	² COS*V	¹ cosV

cos σ,

cos a,

cosV

^: (O, · COS a.

¹ cusV

(2)

(3)

Путем преобразования уравнения (2) можно установить, что

cos* у_ 1

cos* φ 1 - sinV · sin*a ’ так что уравнение (3) примет вид:

COS a , _ч

ω.,= ω. —--τ~τ~ ’ (4

“ ¹ i - sin*?¹ · sin*« ^{4 J}

Из ур-ня (4) следует, что при равномерном вращении одного вала другой будет вращаться неравномерно: ω₂=ацеоэa при <р=0;

О), я со₂⁼ cosa ^ПР^И V ⁼ 2 ^; неравномерность вра-

щения второго вала будет тем больше, чем больше угол между осями валов.

В том случае, когда требуется, чтобы при равномерном вращении одного вала другой вращался также равномерно, необходимо валы соединять промежуточным валом при помощи двух Г. ш., причем вилки промежуточного вала должен быть одинаково наклонены к оси среднего вала (фигура 0). Действительно, при повороте вала А на угол ψ вал В повернется на угол ψ, причем, согласно ур-шо (2), tgψ=tg(/-cosа; пусть вал С повернется на угол /i, тогда tg V=tg ту cos α₂; т. к. а₁== а, то и φ₁=φ, следовательно, в этой системе механизмов * вращение вала А будет в точности передаваться валу С. Легко показать, что если вилки вала В перпендикулярны друг к другу (фи г. 7), то I д Ti= tej ψ cos a cos a₂, τ. e. углы φ_ι и φ никогда не м. б. равны за исключением того случая, когда α=α₂=0, то есть когда оси всех трех валов будут расположены на одной прямой. При угле α= * передача помощью Г. ш. невозможна, и можно сказать, что при α= ^ весь механизм пре

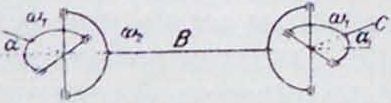
вращается во вращательную пару.

Вместо промежуточного вала В с двумя вилками может быть применена деталь любого вида, имеющая расположенные в одной плоскости втулки для перекладин крестовин А и С; тогда вал В с двумя вилками превращается в муфту Губе, представляющую жесткое сочетание двух вилок ш. Рассмотренные механизмы назы-г и б к и ми соединениями, так

Фиг. двух Г ваются как дают возможность во время работы валов изменять угол a между их осями.

Лит.: Мерцалов Н. И., Кинематика механизмов. Прикладная механика, ч. 1, обработ. М. Фе-ЛИНСКИМ, М., 1916. Б. Шпринк.