> Техника, страница 41 > Гюйгенса принцип

Гюйгенса принцип

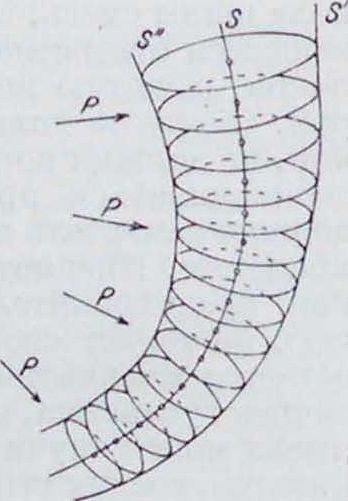
Гюйгенса принцип, тооретич. правило, введенное впервые (1696 г.) Гюйгенсом и упрощающее изучение распространения волнообразного (колебательного) движения в сплошной однородной среде. Волновой поверхностью, как известно, называется поверхность, во всех точках которой колебательное движение имеет одну и ту же фазу (смотрите Волны). Пусть S—положение волны в момент времени t. Па фигура изображена ли нии пересечения поверхности S с плоскостью чертежа. Пусть стрелки Р указывают направление распространения волны до прихода в положение S. Каждая точка поверхности S рассматривается как центр повой волны; каждую такую волну назовем элементарной. Элементарные волны в изотропной среде будут сферическими, в анизотропной—более сложной формы. Все элементарн. волны через промежуток времени М после момента t займут некоторое определенное положение в пространстве. Па фигура показано пересечение их с плоскостью чертежа для некоторых точек поверхности К. Элементарные волны имеют две огибающие поверхности S и S"—одну впереди, другую позади волны.

Г. ii. устанавливает, что истинное положение волны в момент времени + Д будет положением огибающей поверхности S. Другая огибающая поверхность S" физическ. значения не имеет. Скорость передвижения волны (для изотропной среды) равна расстоянию между S и S, деленному на время М. Гюйгенс применял это правило для объяснения распространения света, к-рый он считал колебательным движением особой невесомой упругой материи, наполняющей пространство,—эфира. Он доказывал необходимость существования эфира, рассматривая интерференций) колебаний, происходящих в различных точках среды между S и S" от отдельных элементарных волн. Слабым местом его рассуждений является объяснение отсутствия обратной волны S".

Более строгая, но все же не вполне совершенная формулировка и разъяснение Г. п. были даны О. Френелем на основании принципа интерференции (1822 г.). И руках Френеля Г. н. сделался могучим средством как для объяснений уже известных в его время явлений интерференции и диффракции, так и для открытия новых явлений, что и привело в первой половине 19 века к общему признанию волновой теории света вместо господствовавшей до того времени теории истечения Пыотояа. Вполне строгая математическая формулировка Г. и. для среды, волновое движение которой управляется т. н. вол и о в ι,ι м уравне я и е м

04» j_ ·>’γ Ον __ i ον q

Οχ³ ‘ Oy³ ‘ Oz² c* Ot* ’

дана Кирхгофом.

С математической точки зрения Г. и. является преобразованием интеграла волновой функции ψ, распространенной по объёму, в интеграл, взятый по поверхности. Комбинация теоремы Грина и вышеописанного волнового уравнения приводит к следующему выражению Г. и.:

fu» (	1 1 _ §ψ	1 0ψ	dr]
J L · On l r,	1 r On c	r * 01	On j

где ψ·—волновая функция, г—расстояние рассматриваемой точки от данной произ-

вольной замкнутой поверхности, по которой производится интегрирование, п—внутренняя нормаль к элементу поверхности, с— скорость света, <1а—элемент поверхности, «(0)—значение ψ в данной точке. Вполне точное решение задач о распространении волн в среде, в частности задач диффракции, достигается непосредствен, решением волнового уравнения при данных граничных условиях. Этот прием представляет, однако, очень большие математические трудности.

Лит.:×в о л ь с О н О. Д., Курс физики, т. 2, Берлин, 1923; ф р e u е л ь О., О свете, Москва— Ленинград, 1928; Driiile Р., Lchrbucli der Optik, Leipzig, 1913: liuyghens Cti. Traitft de la lii-midro, Paris, 1920; P (linear и II., ThCorie mathO-matique de la iumiftre, v. 2, Paris, 1892: Planck M., Einlilhrung indie theorctische Physik, B. 4, Leipzig, 1927. H. Фредерикс.