> Техника, страница 41 > Двигатели внутреннего сгорания

Двигатели внутреннего сгорания

Двигатели внутреннего сгорания, двигатели, в которых внутри рабочего цилиндра химическая энергия топлива преобразовывается в энергию тепла, превращаемую помощью кривошипного механизма в механическую работу.

Топливо и реакция сгорания. Для Д. в с. топливо бывает трех родов: газообразное, жидкое и твердое. Жидкое топливо при введении в двигатель перед сгоранием испаряется или расггыливается в мелкий туман; твердое топливо путем разложения и частичного сгорания предварительно обращается в горючий газ, к-рый вводится в цилиндр двигателя; продуктами сгорания всякого рода топлива являются также газы. Поэтому все двигатели внутреннего сгорания можно рассматривать как двигатели, работающие на газообразном топливе.

Основной состав топлива. Основными химическими элементами, тепло сгорания которых используется в Д. в с., являются углерод и водород. Из различных химическ. соединений углерода с водородом широкое распространение как топливо для двигателей получили следующие группы: 1) группа а р о м ат и к о в вида С„Н_2п__в, относящаяся к циклическим соединениям: бензол С₆Н„, С₇11, ксилол С₈11,₀; 2) группа олефинов вида С_ПП_2П: этилен С_гН₄, пропилен С₃Н₀, бутилен СД1₈ ит. д.; 3) группа параф и ц о в вида С„ Н _2п+,—предельные углеводороды: метан СИ, этан С₂И₆, пропан С₃Н₉, бутан С₄Н_1в, пентан С₅Н,_г. гексан С„11_и, гептан С₇11_]6, октан СД1_]8, три-декан С,₃11_2Я ит.д. Большинство непредельных углеводородов, слабо оводороженных, не могут применяться в двигателях непосредственно, так как неустойчивые соединения легко дают смолы, оседающие на рабочих органах двигателей, и лишь в последнее время они нашли применение в специальных конструкциях форсунок с пневматическим распыливаниом при сжигании совместно с предельными углеводородами. Большинство видов жидкого топлива представляет собою смесь различных углеводородов разных точек кипения, и потому они не могут быть выражены простыми химическими формулами. Для таких топлив процентное (по весу) содержание всех входящих в них элементов определяется химическим анализом (табл. 1).

Таблица 1.— Состав жидкого т о п л и η а в весовых %.

Вид топлипа	с	Н	О
Керосин.	86.32	13,24	0.44
Нефть.	85,90	13,03	1,07
Бензин.	85,43	14,57	0,00

Химические реакции. П роцесс горения всякого топлива сводится к окислению его составных частей, и продуктами полного сгорания являются: углекислота и водяные пары. При этом объёмы газов, вступающих в реакцию, до и после сгорания не остаются постоянными. Если имеется углево-дородистое соединение вида C_mII_nO_r“, то реакция происходит по формуле:

l*»C_mH_nO_r+(m + "-) .и³ 0,=

= т м³ СО, + ” м³ Н₂0.

Зная количество теоретически необходимого кислорода, легко вычислить и теоретически необходимое количество воздуха:

т 4 -

г__* ² _л,3

- 0,21 ^М

(1)

где 0,21—доля объёмного содержания кислорода в воздухе; точнее брать число 0,209. До реакции смесь горючего с воздухом может содержать количество последнего L, большее теоретически необходимого. Отношение п= называется коэффициентом из-

бытка воздуха. Разницу в объёмах газов (ΛΓ) до и после сгорания легко получить, вычитая из объёмов газов после сгорания объём их до сгорания:

Δ7. (2)

Изменение объёмов не зависит от количества атомов углерода (т), входящих в состав данного соединения, а зависит лишь от числа атомов водорода (п) и кислорода (г).

Теоретически необходимое количество воздуха в килограмм о леку л ах на 1 килограмм топлива:

1

0.21

m + —

4 2

?сг-мол.

(3)

12т + л + 16r

Изменение числа килограммолекул при сгорании определяется как разность:

AM =

т п

12m + и + 16r ^г 2(12m + η + 16г)

т+ -4 2

4⁺2

12т + л + 16г 12т + п+16г кг-МОЛ.

(4)

Теплотворная способность топлива. Теплотворной способностью топлива II называется количество калорий, выделяемое при полном сгорании его единицы (объёмной или весовой) и определяемое калориметром Юнкерса или и Крекера, то есть при постоянном давлении Q_p или при постоянном объёме Q_r. Разница между величинами Q_p и Q_v незначительна, и на практике ей пренебрегают. В Д. в с. нельзя использовать всего тепла, выделяемого топливом, так как часть его теряется в виде скрытой теплоты парообразования, затраченной па испарение образующейся при горении воды, вследствие высоких температур отходящих газов. Поэтому отличают высшую теплотворную способность, без вычета этой затраты тепла, и низшую, или рабочую, учитывающую эту потерю. Так как

* Для применения указанного метода расчета для нефти и ее отгонов принимают следующие приближенные формулы: для нефти Cull,, для керосина Cull, и для бензина С,11,.

темп-ра отходящих газов в Д. в с. высока и, следовательно, вода, находящаяся в продуктах сгорания, уходит в виде пара, унося с собой скрытую теплоту парообразования, то на практике приходится считаться только с низшей теплотворн. способностью. Теплотворную способность, отнесенную к весовым единицам, будем обозначать через /t, причем низшую теплотворную способность—через h_u. Те же величины, отнесенные к 1 м³, в дальнейшем будем обозначать через II и II,.

Для водорода, который находится в газообразном состоянии, высшая теплотворная способность, отнесенная к 1 килограмм, будет: /i=34 100 Cal. При сгорании 1 килограмм водорода получаем 9 килограмм воды. Считая скрытую теплоту испарения г ^ 600 Cal/кг, получаем из высшей теплотворной способности рабочую (низшую):

h„=h - 9 г=34 100 - 5 400 -= 28 700 Cal/кг. Низшая теплотворная способность водорода, находящегося в химическом соединении с углеродом, по Менделееву, равняется h„=24 000 Cal/кг.

Теплотворная способность 1 килограмм топлива группы С_ПН_П и С_пН_2п не зависит от числа атомов углерода и водорода.

Характеристические постоял-н ы е. Характеристическ. постоянную (К) после сгорания можно найти из изменения объёмов до и после сгорания. Для начального состояния G_t весовых ед. смеси имеем: Ρ,Ε,== GjEjTj; приведя продукты сгорания к первоначальным давлению Р, и температуре Т„ получим после сгорания: P₁V_i=G₁R_i Ί, от-

куда р“ =гр^?, или, принимая во внимание, что Vi=V, + AV, имеем: р“=^V * ^AV=β, или

iit V ι

βR₁. Если объём после сгорания увеличивается, то ΛΕ берется со знаком +, если уменьшается, то со знаком —.

Средний химический состав наиболее употребительных видов газообразных топлив, их теплотворная способность, а также теоретически необходимое для их сгорания количество воздуха приведены в таблице 2 и 3.

Теплотворная способность рабочих смесей. Так как в двигатель засасывается не чистое топливо, а смесь его с воздухом, то практически на количество тепла, выделяющееся за один рабочий цикл, оказывает влияние не теплотворная способность самого топлива, а та же величина, отнесенная к единице объёма рабочей смеси. Если на 1 м³ газа для его сгорания тратится L м³ воздуха, то теплотворная способность смеси будет

II=-^Ни-

9 1+ L

(5)

т. к. тепло 1 .и³ газа будет теперь заключаться уже в (1 + L) м³ смеси. Два рода топлива, из которых один имеет теплотворную способность большую, чем другой, не всегда дают такое же соотношение и для их рабочих смесей:

Для нефти..h_u — Ю 000, Нд=800

» 90°-ного а. h_u=5 630, Нд =* 827

» окиси углерода. .. . Н_и=2 800, Нд=828

» светильного газа. .. Н_и *» 4 590, Нд «=» 739

*с>

Газ ы	Молеку лярный вес /<	Теоретически необходимое количество в м% кислорода для сжигания i .«* газа s„	Теоретически необходимое количество в м“ воздуха для ежи гания 1 м“ газа L.	Уменьшение объёма при сжигании 1 м“ газа Л V	Высшая теплотворная способность 1 килограмм газа в Cal h	Низшая теплотворная способность 1 килограмм газа в Cal h«	Высшая теплотворная способность 1 аГ газа при 15° и 1 aim в Са1 Н	Низшая теплотвор пая способность 1 м“ газа при 15“ и 1 aim в Са1 Пи
Окись углерода СО.	„	0.5	2,38	0,5	2 440	2 440	2 800	2 800
Водород ΊΙς.	2	0.5	2,38	0,5	34 100	28 700	2 800	2 360
Метан СИ,..	16	2	9,52	0.0	13 250	И 900	8 700	7 820
Ацетилен С,И,.	26	2.5	11.9	0,5	12 000	11 600	12 800	12 360
Светильный газ.	12.58	1.10	5,21	0,275	9 960	8 900	5 135	4 590
Водяной газ.	15.66	0,45	2.15	0.45	3 930	3 580	2 520	2 300
Генераторный газ (силовой).	24,25	0.21	1,00	0.21	1 180	1 100	1 175	1 095
Доменный газ.	2S. 48	0,16	0,76	0,16	768	757	896	885

Т a G л. 3.— основные вел и ч и нм для с г о р а п и я ж и д к о г о т о п л и в а.

Вид топлива	Молекулярный вес И	Темп-ра кипения t$	Высшая ΤβΠ-лотворн. способность дли 1 килограмм в Са1 h	Низшая теи-лотворн.способность для 1 килограмм в Са 1 >‘и	Теорет. необх. колич. нислор. в .и“ при 15° и 1 aim для 1 килограмм S.
голь С2НвО.	46	78,3	7 100	6 400	1.59
95 весовых %.	—	78,5	6 740	6 000	1,51
Бензол СвН6..	78	80.4	10 000	9 590	2,35
Бензин ..	—	80—110	10 500—11 200	10 400	2,7
Керосин..	“	200—250	10 500—11 000	9 800—10 200	2,7

Из приведенных примеров видно, что топливо более бедное иногда оказывается более выгодным.

Процесс сгорания. Теплотворная способность Н топлива, определяемая практически по количеству тепла, выделившемуся в воду, при его полном сгорании в бомбе Крекера или же в калориметре Юнкерса, всегда меньше полного тепла химической реакции, потому что часть последнего идет на повышение внутренней энергии продуктов сгорания, имеющих иную теплоемкость, чем рабочая смесь. Эта разница, благодаря зависимости теплоемкости от температуры, будет изменяться с температурой, при которой ведется опыт, и будет тем больше, чем выше температура. По подсчетам, произведенным Гребером, средние молекулярные теплоемкости таковы:

	При посто	Я II II 0 м	объёме (с„)
для	простых газов.	, μθν	= 4,625 + 0,00053 Г
»	углекислоты.		= 6,774 + 0,00189Т
	водяного пара.	μθ" V	= 6,855 + 0,00116Т
При постоя		н и о м давлен и и (ср)
для	простых газов.	рс·	= 6,610 + 0,00053Т
»	углекислоты.	· 4	= 8,759 + 0,001897
»	водяного пара.	4	= 8,840 + 0,001167

Такое уменьшение теплотворной способности становится ощутительным лишь при высоких температурах, а потому с достаточной для практики Д. в с. точностью молено считать величину II„ постоянной. Если предположить, что процесс сгорания совершается при постоянном объёме, то все тепло реакции пойдет на приращение внутренней энергии U за счет: 1) повышения температуры, 2) увеличения суммарной теплоемкости продуктов сгорания по сравнению с ра бочей смесыо. Это может быть выражено следующим уравнением:

dQ — dU, (61

или, интегрируя, получим:

Q-U_t-U_%,

Q (Cp)m 1 ι~ б,)m 1 ( ‘

[где Q—тепло реакции, (сД„ и (с,),—средние теплоемкости газов до и после сгорания], или

. Я_и + (сх г,=(о;,; т₂. (8)

Если сгорание протекает при постоянном давлении, то все тепло реакции идет на повышение теплосодержания J. Из основного уравнения

dQ — dJ — Αν dp, принимая dp=0, найдем: dQ=dJ,

или, интегрируя,

Q=.J₂-Jy,

Q + (Cp);„ Ту=(с,)" Г,. (0)

Заменяя Q через IIполучаем:

1Ι„ + (βρ)ιη 1 1~ 0p)m I 2* (Ю)

Считая средние теплоемкости зависящими от температуры по закону

(pv)m ~ Н V Έ 1 ?

С^р)т ⁼" Έ Ь_П1 1,

можно придать уравнениям (8) и (10) следующий вид:

1) для сгорания, при v= Const,

Я„ + (αί -j- Ь_ш Ту)Ту=(«0 + bп Т.,)Т₂; (11)

2) для сгорания, при р=Const,

+ (а_р -[- b_ш Ту)Ту=(ар -f- Ь_п, Т_а)Т,. (12)

I Oil

UU

Имея характеристич. ур-ия рабочих газов до (PxVj=Β-,Τ-ι) и после (р₂г₂=Л₂У₂) сгорания, можем для процесса сгорания определить соотношения объёмов и давлений: 1) v= Const:

Ра_ I jlli.

Pi ~ t,R, ’

(13)

но откуда

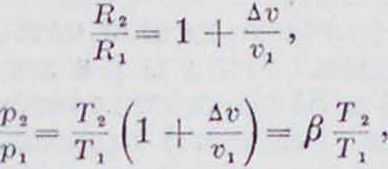
где Лг—изменение объёма от химической реакции, приведенное к первоначальному состоянию (изменение числа молекул);

2) р=Const:

г, __ Т_tII, о, ^_ Т, R, ’

или, но предыдущему,

а

Г|

Г,

Г,

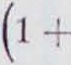
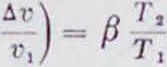
где Л г—изменение объёма от химической реакции.

Основные процессы при переменных теплоемкостях. Показатель адиабаты. Отношение ^,р, то есть показатель адиабаты к для

^се данного процесса при переменной теплоемкости, не есть величина постоянная, а зависит от температуры. Действительно:

к--=

1.985

, С„ — С„=- а

C_P’ Р ⁰ μ

где ц молекулярный вес, откуда

1.985. и *

Гр=+

разделив на с_с, получим:

_fc= 1,985 ₌ j

μ€_Γ

о · Ь I

(14)

В виду весьма пологого протекания кривой к в зависимости от Т (фигура 1) выражение

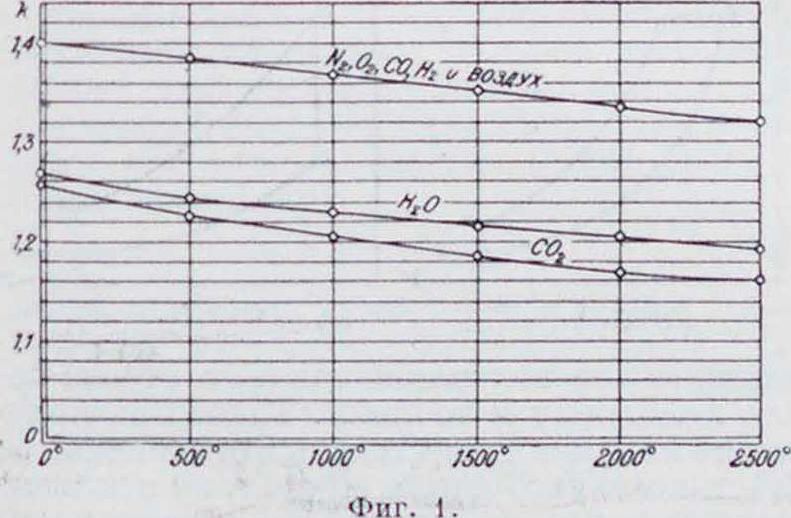
(14) может быть представлено уравнением прямой:

к=к₀ — гТ и для двухатомных газов к=1,422 -Уравнение адиабаты

0,572 Т

Id 000

c_r (ГГ + ар dv=0

при переменной теплоемкости примет вид:

Гг“ ¹ h,-l-rT

Const.

(15)

Из этого ур-ия можно вывести и следующие два ур-ия адиабатического процесса для двух состояний газа:

ГТ(А,-1-гТ.П 0	(1C)
|_Г0(“,- 1 - rTj J
k,~l
rT, /у_ гТ о ho ~ 1 Y*V 1 h0 — 1	(17)

По этим двум ур-иям можно всегда, зная начальное состояние газов, определить конечное, и наоборот. р

Уравнение д л я политроп ы при переменных теплоемкостях получается в виде:

1 ~vk,

ЙДД-rW=^Const>

(18)

где у—доля тепла, идущая на повышение внутренней энергии.

Для двух состояний газа имеем:

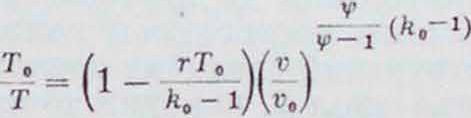
гг

k, - i

(19)

Ур-ие адиабаты получается из данного ур-ия политропы при=1. Последнее неопре деленное выражение можно определить нз основного ур-ия адиабаты:=— 1. Под ставляя вместо c_r dT его значение V’ dQ и вместо A dL его значение (1—ψ)<2Q,получим:

r_rdT Λ dL

V

1 - у

-1, откуда -“·= 1.

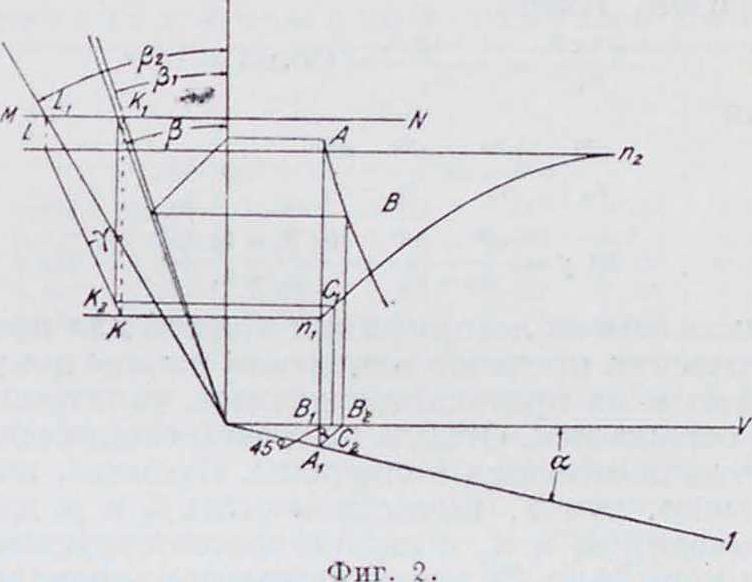
Построение политропы при η ф Const. Даны оси координат Р, V, точка А политропы и кривая п,п₂—значений показателя η (фигура 2). Пользуясь основным соотношением Брауера:

1 + tg β=(1 + tg α)“,

видим, что, при пфConst, и β есть величина переменная. Обозначим 1-j-tga через а. причем, при выбранномА а, а есть величина постоянная, и прологарифмируем это выражение:

lg (1 + tg β)=nig a. (20)

Вычислим A /?, для значения щ (по кривой п_л щ) и построим соответствующий луч. Проводим произвольную горизонталь MN и точку пересечения ее с этим лучом К₁ сносим на горизонталь, проходящую через Эту точку К примем за начало кривой (1 + tg/?), осью абсцисс которой является вертикаль, отстоящая от оси р на расстоянии, равном 1. Если за ось абсцисс принять ось Р, то искомая кривая есть кривая tg β. Построить эту логарифмпку молено по уравнению (20), вычисляя соответствующие углы β; но этого вычисления можно избежать, зная, что для небольших пределов изменения числа пропорциональны своим логарифмам; тогда ло-гарифмика для этих пределов м. б. заменена прямой, проведенной к вертикали под^у, значение которого определится следующим образом. Имеем:

или

1 + tg β,	1 +tg(3,
η»	я“
α”1	α”· α"* -
η,	η, η, -
tgy =	αWs - αηι
	η,-η,

Const=tg у,

—=Const, η.

tg β, - tgP,

η, — η,

Такая замена логарифмики прямой для практических пределов изменения вполне допустима и па протекании искомой политропы не отражается. Отсюда получаем следующий метод построения политропы. Проведя, как обычно, луч 1, вычисляем углы β₁ и /?₂ для значений n_t и п₂ и строим соответствующие им лучи (фигура 2); затем проводим произвольную горизонталь MN и точки пересечения ее с лучами L_l и К_х сносим на соответствующие горизонтали, проходящие через точки я, и п₂ кривой п. Соединив эти точки, получим искомую прямую LK, образующую с вертикалью угол у. Затем из точки А проводим вертикаль AA_lt а из А_г—прямую под Z45° к оси V. Полученный отрезок делим пополам и из точки С_г проводим вертикаль до пересечения с кривой п в точке С,; из С, ведем горизонталь до пересечения с KL в К_г и обычным построением находим угол β, соответствующий среднему значению п (точка С г). Зная угол β, находим точку В искомой политропы по методу Брауера. Построение следующих точек производится в таком же порядке.

Общие положения четырехтактных и двухтактных циклов. Рабочий никл современных Д. в с. осуществляется по схеме, которая по своим основным фазам весьма близко подходит к циклу Карно. Отличие от цикла Карно заключается главным обр. в способе как получения тепла, так и отдачи его холодному источнику. По ци-, клуКарно, получение и отдача тепла должны идти по изотермам, т. к. лишь при равенстве темп-ры источника с темп-рой рабочего тела возможно получить обратимый процесс с соответствующим максимальным теплоиепользоваиием. Т. о., рабочий цикл Д. в с. будет состоять из двух произвольных линий, по которым получается тепло (линия сг) и отдается тепло (линия еа), и двух адиабат: адиабаты сжатия ас и адиабаты расширения ге (фигура 3). Все практически осуществленные циклы различаются

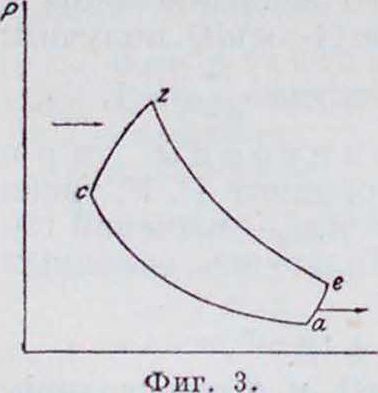
между собой характером протекания линий получения и отдачи тепла, причем сообщение тепла осуществляется или по изоплере (линии постоянного объёма), или по изобаре (линии постоянного давления), или, наконец, частью по одной, частью по другой прямой; отдача тепла совершается по р=Const или по t;=Const.

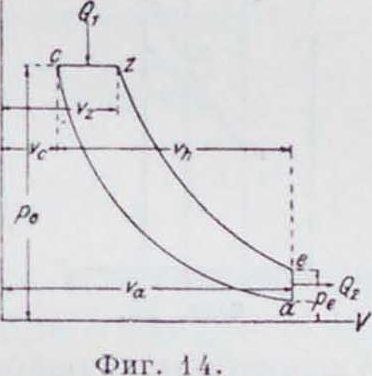
Далее, различают циклы четырехтактные и двухтактные. Четырехтактный цикл (фигура 4 и 5) осуществляется след. обр. По линии оа (1-й такт) происходит всасывание рабочей смеси (или чистого воздуха), но ас—сжатие ее (2-й такт); воспламененная

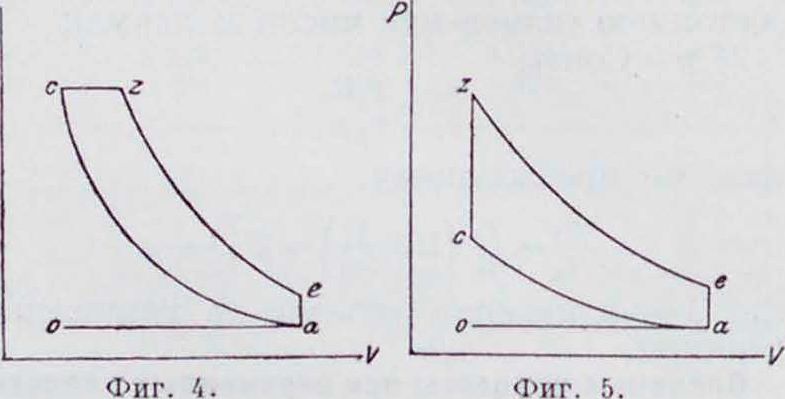
в точке с смесь сгорает по линии постоянного объёма или давления (сг). По ге происходит расширение сгоревших газов (3-й такт), по еа—уравнивание давлений с выпуском продуктов сгорания и, наконец, по ао (4-й такт)—выталкивание оставшихся продуктов сгорания в атмосферу. В случае д в у х-тактного цикла (фигура 6 и 7) линии всасывания и выталкивания (1-й и 4-й такты) отпадают и заменяются линией продувки ао. Для простоты делается предположение, что рабочий процесс осуществляется по обратимому циклу; в таком случае можно принять, что по линии сг происходит не сгорание, а простое сообщение тепла извне, а по

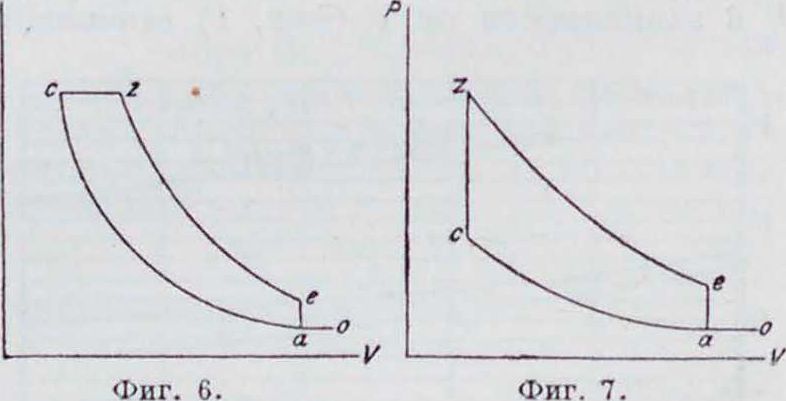
линии еа—не вытекание газов, а отдача тепла холодному источнику. Такое предположение никаких существенных отклонений от действительного цикла не дает, за исключением линии еа, по которой изменяется количество газов вследствие вытекания, почему состояние рабочего тела по этой кривой не м. б. определено из обычного характеристического уравнения. Далее, предположим, что теплоемкости газов постоянны и не зависят от темп-ры. При термодинамич. исследовании теоретич. цикла линии всасывания и выталкивания в четырехтактном двигателе и линия продувки в двухтактном двигателе м. б. исключены из рассмотрения, так как: ^алгебраическая сумма работ газа, соответствующих этим тактам, равна нулю; 2) рабочий процесс в этот период протекает с пере-

менным количеством рабочего тела и потому является необратимым. Для рассмотрения отдельных циклов, осуществляемых в Д. в с., введем следующие общие понятия и обозначения для всех циклов. Рабочим объёмом цилиндра V_h назовем объём, описываемый поршнем между его крайними мертвыми положениями; объёмом пространства сжатия У_с—объём, в к-ром заключена рабочая смесь в конце сжатия при положении поршня в мертвой точке; сумму объёмов V_r+V_h обозначим через V_а. Степенью сжатия ε назовем отношение объёмов в начале и в конце сжатия ε,степени предварительного расширения <, и степени увеличения давления Л. Если в указанной формуле подставим (<=1,то смешанный цикл превращается в нормальный, т. н. цикл Отто, и

1-ал·

Из этого выражения для г_п, выведенного в предположении постоянных теплоемкостей, видно, что термический кпд зависит исключительно от степени сжатия ε и показателя к, с повышением которых он растет. Зависимость 7j_t от ε и к дана в таблице 4.

Таблица 4. — Кпд щ для цикла быстрого сгорания (Отто) при различных е и ft.

k	2,0	2,5	3,0	3,5	4,0	4,5	5,0	6,0	7,0	8,0	9,0	10,0
1.20.	0,129	0,167	0,197	0.221	0.242	0.260	0,275	0,301	0.322	0,340	0,356	0,369
1.25.	0.159	0.205	0.270	0.279	0,293	0,313	0.331	0,361	0.385	0,405	0.423	0.438
1,30.	0.188	0.241	0,281	0,318	0.340	0.363	0,383	0.416	0,442	0,464	0,483	0.499
1.35.	0.216	0.274	0.319	0.355	0.384	0.4-.9	0.431	0.466	0,494	0.517	0.537	0,553
1 40.	0,248	0,313	0,363	0,402	0,434	0,460	0,483	0,520	0,550	0,574	0.594	0,610

сжатия, то есть ε=у. Объем и давление в конце сгорания обозначим соответственно через V, и у,. Степенью увеличения давления при сгорании h, если оно имеет место, назовем отношение давлений в конце и в начале сгорания, то есть Я= Степенью предварительного расширения р назовем отношение объёмов в конце и в начале сгорания, то есть (>= у^! · Тогда степень расширения 4, представляющая отношение объёмов в конце расширения и в

t V,

конце сгорания, выразится так: о=~ ·

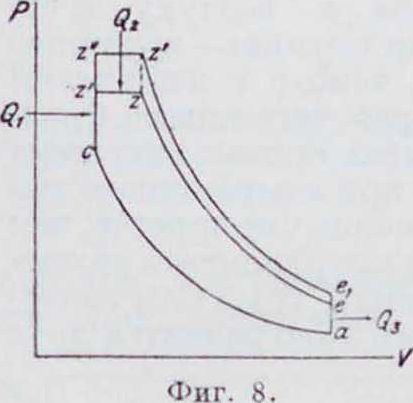
Термический кпд. Как общий случай рассмотрим рабочий процесс, в к-ром часть тепла Q, Cal сообщается по линии v =Const, другая часть (,)₂ Cal—по линии р =Coust; холодному источнику отдается Q_a Cal (фигура 8). Термический кпд

(21)

Qi + Qi

Выразив тепло через температуру и теплоемкость ρ,=с, (Ту - Г,.), - Ср (Т, - Ту),

ρ,= с„(Т,-Т_в) и вставив эти выражения в ур-ие (21), получим:

Vt =* 1 -

Т_е - Т„

(22)

ту - Тс + кСГг-Т,)

Выразив все темп-ры, входящие в это ур-ие, через темп-ру Т₀, пользуясь вышеприведенными обозначениями и ур-иями адиабаты: Т_с =Т_ае^к~¹,

Ту =λΤ_β=λε*-ιΤ_β,

Т_а =» ρΤ у =(.λε*-ΐΓ_β,

т„=т_г(^е4)·¹=р“;.т_а,

получаем после подстановки:

1 -1

b- 1-,

(23)

ек-1 Л — 1 4- ft/.((?— I)"

Т. о., термический кпд смешанного цикла зависит от показателя адиабаты к, степени

Из табл, видно, что с повышением к при одном и том же ε термический кпд возрастает; такая яге зависимость существует между 11, и ε при одной и той яге величине к. Подставляя в формулу (23) λ= 1, получаем кпд для так называемого цикла Дизеля 1 i е“-1

ek-l Λ(ρ - 1)

Из этого выражения видно, что для двигателя Дизеля термический кпд зависит, кроме ε и к, еще от степени предварительного расширения ρ. Чем больше ρ, тем меньше η, и так как ρ увеличивается с ростом нагрузки, то η. Дизеля повышается но мере убывания нагрузки. Зависимость г/, цикла Дизеля от ε и ρ приведена в таблице 5.

Та 0 л. 5. — Кпд rit цикла Дизеля при различных е, ft и д.

ft	6 ε	1,50	1,75	2,00	2,25	2,50	2.75	3,00
1,30 1,41	16 13	0.535 0.616	1 0.522 0.512 0,602 0,588		0.499 0.576	0.48S 0.479 0,564 0.552		0,471 0,540

Для определения влияния отдельных факторов на термический кпд и их взаимные отношения необходимо проследить изменение термическ. кпд в зависимости от одной лишь переменной, в то время когда другие величины имеют какие-нибудь постоянные значения. Основной вопрос, который возникает у исследователя: каким образом должно быть подведено тепло для того,чтобы обеспечить максимальное его использование. В смешанном цикле это тепло состоит из тепла, сообщенного по 4>=Coiist и но 7J=Const. Пред-положим, что количество тепла Q« не меняется, а меняется лишь относительное значение Qi и О_г,так что сумма Q=Qi+Qi==Const. Имеем:

Qi - с„(Ту - Т_с) - с_сТ_с (-£-1)=c_vT_c(λ -1), Q*=c_p(T,-Ty)=c_pT_z· (g-l) -c,Tyfe—1),

Qi + Qi=C_VT_C(X -1) + c_pT_zie-1)=const,

^Q‘ + ^Ql=λ -1 + U(Q-1)=Const. (24)

^CVL C

При постоянной теплоемкости и постоянной степени сжатия, с и Т_с суть величины постоянные, н вся левая часть уравнения также постоянна. Полученное выражение (24) позволяет при постоянном сообщении тепла определить связь между Я и (>. Задаваясь

Vi^%

—

ρ-

J

P<°

r="

Λ

V

Δ

1

Фигура а. разными значениями для/., определяя соответствующие им значения у при данном количестве сообщенного тепла Qi+Q₂ и подставляя полученные значения в формулу термического кпд (23), найдем изменения η, при вышеуказанных условиях, изображенные на фигуре 9. Здесь жирные кривые соответствуют термическому использованию при постоянном сообщении тепла, в зависимости от изменения и Я, а тонкие кривые η, в зависимости от изменения Я и количества сообщенного тепла, — при постоянном ().Этн кривые построены для степени сжатия е=15 и показателя к=1,4. При Я=1 получим значения η, для разных Q, которые соответствуют нормальному циклу Дизеля; при(>=1 получаем значение η, для цикла Отто. Так. образом, с левой стороны диаграмма ограничена вертикальной прямой Я=1, а сверху—прямой (=1. При постоянном количестве сообщенного тепла смешанный цикл, но мере удаления от цикла Дизеля и приближения к циклу Отто, повышает кпд. В пределе, когда все тепло сообщается по «=Const, термический кпд, независимо от количества сообщенного тепла, для всех кривых получится одинаковым. Если, при данной степени предварительн. расширения (/,

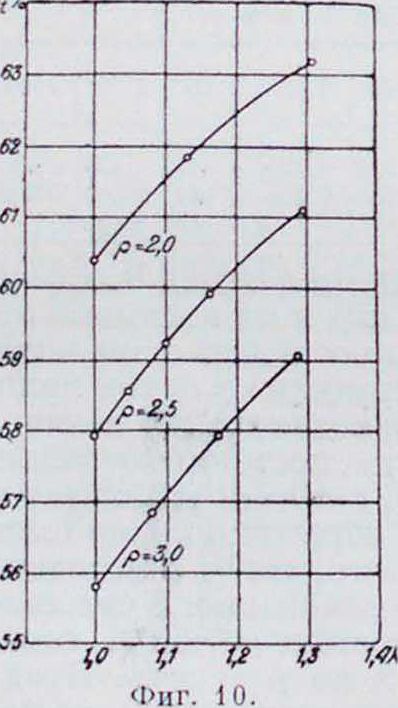
увеличить Я за счет большего сооощепия тепла, то η_t последнего цикла несколько увеличится. Таким образом, кпд диаграммы асz ze меньше кпд диаграммы aczze₁ (фигура 8). 11а фигура 10 представлены изменения кпд в зависимости от практических изменений ρ и Я в пределах <<=2,0-^-3,0 и Я=1,0 — 1,3, как они имеют место в двигателях, которые работают по этому циклу.

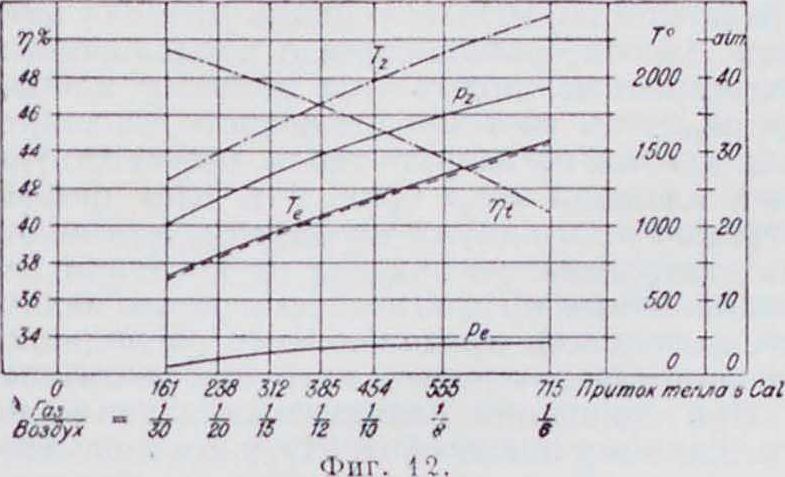
Сравнение циклов при постоянной и переменкой теплоемкостях. Зависимость величины у, от состава рабочей смеси при постоянной и переменной теплоемкостях представлена графически на фигуре 11 и 12, причем первая относится к случаю с=Const, а вторая— кп переменному. Ilo оси абсцисс отложены величины теплотворных способностей смеси и соответствующие нм отношения количества газа 1C воздуху, а по оси ординат—величины ?/, темп-p Т и давлений р рабочего цикла. Сравнивая кривые этих двух диаграмм, Видим, что при с переменном падение щ по мере обогащения смеси резче, чем при с постоянном. Для коэффициента смешения у» (соответствующего i G1,3 Cal) значения для обоих случаев мало разнятся друг

		~T~
						^ 1
	___				A	h
						— 7i
		У		A
		7		j
			7
					-Λ-	—	—

г

3000

2500

2000

1500

1000

500

О

’6! 256 JL 2. 50 го

555 ‘U 1 1 17 гд

565 1

7

715 Лриюо“ те/1ла $ СЫ 7

Фигура 1 1.

от друга (50,5 и 49%),тогда как для смеси богатой (Ve) разница достигает 7% (48 и 41 %).

Из рассмотрения каждой из этих диаграмм в отдельности можно проследить зависимость р и Г начала и конца расширения от состава смеси. По мере обогащения смеси,р и Т соответственно возрастают, вследствие чего увеличивается теплоемкость рабочей смеси, уменьшается к и понижается термическое использование в двигателе, что видно и из выражений:

i ¹ t I¹* ^{- 1}

ч“ ~ 1 ^— «ITT ¹¹ ~ * h (ρ

(Отто) (Дизель)

Следовательно, для данного рабочего тела кпд находится отчасти в обратной зависимости от температуры. Т. о., и здесь подтверждается заключение, что при определенной наивыгоднейшей степени сжатия t работать с бедной смесью лучше, чем с богатой.

Цикл Отто (при с Ф Const). Даны Q, * и состояние точки а (фигура 13); рабочий цикл совершается двухатомным газом. Но уравнению адиабаты, при с ф Const,

или

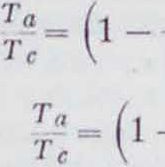
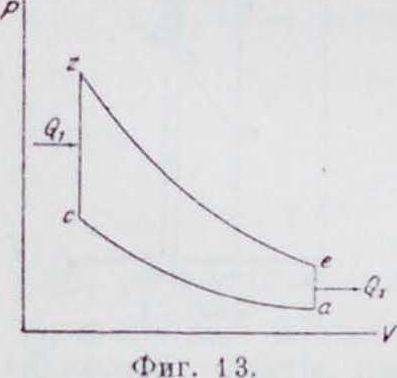
гГп (VAk.~l

+

·,)©

гТ„ к, - i ’

гТ а

(25)

определяем температуру в конце сжатия Т,. Зная количество сообщенного тепла Q_lt определяем температуру вспышки Т_г по ур-ию Qi + (a_v + b,„ Т_с) T_e=(α„ + b,„ Ί )Τ„ причем все значения и (a+b_mT) м. б. взяты по отношению либо объёмных, либо

р

весовых единиц, a b_m относится к средней теплоемкости. Температуру в точке е определяем по ур-ию адиабаты:

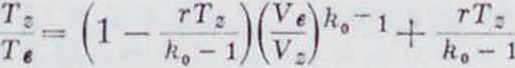
или

:=(l _ -ίϊΐ-Vt -I- Jh.

. V -1 ^ K-i

Зная температуры рабочего цикла, находим термический кпд:

Vi

1 Q» 1 _ [о“ + ^ь<" <^т«+ Ы} (Т,-Тд) Ql ¹ Qi

Для примера определим кпд при постоянных и переменных теплоемкостях для цикла Отто, для степени сжатия е=5, при сообщении 500 Cal тепла на 1 килограмм рабочего воздуха, при начальном состоянии воздуха, соответствующем точке а, 1 atm и 300° К. При с= Const.

1 — 7*1,=1 —=1 — J=0,183.

При с Const для воздуха к=1,422

0,572 rji. 7. 10 000 ¹ ’ ^,1°

1,422;

0,572 10 000 ’

300 _ Λ__0,572 - 300 _1___L 0,572-300

tc 0 ,432 - 10 0(Ю 5⁰’*^{22 1} 0,422 · 10 000

откуда У_с — 5(38°.

Пишем уравнение сгорания, относя все величины к 1 тсе-мол.: для воздуха (ц =20) (+=π 500=29 - 500; а, + b,„ Т=4,625 + +0.00053Т; 29-500+ (4.625+ 0,00053-568)568 -= (4,625 + 0,000537V)7., откуда Т_г=2 830.

Для адиабаты расширения имеем:

2 830 Λ 0,572 · 2 830 -_n, 0,572-2 830.

Те ~ V 0,422 · 10 000)° ’ " 0,422 · 10 000 ^г

²,^°=1,599; Т_е=1 770=;

Vi= 1 -

Г4,625 + 0,00053(300+1 770)1(1 770-300)

29 500

= 0,121.

Цикл Дизеля (при с Ф Const). Даны (i и « и состояние точки а; цикл совершается двухатомным газом (фигура 14). Как и в цикле Отто, характерные температуры Т„, Т_г и Т_е можно последовательно определить из следующих уравнений:

пли

Тп /, _ гТ_я /VA/t„ 1^ гТд

Tc ⁼ V к- )[ ’а) ><о^-1 *

/. _ ГТд 1, ГТд.

Тс ^ fe.-ljeft,-‘‘^r К- 1 ’

т.= еТ_с;

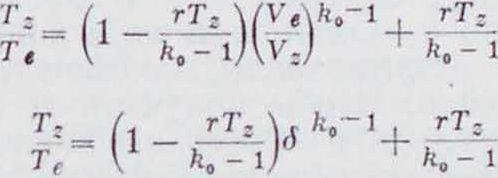
На основании полученных температур термический кпд двигателя выразится:

1 _ϋΐ₌ 1 _ l°g + bm(T_g+T₀)l(r_t -Та) ^η* QI [Ор + 6я,(7’с+ T*)I(X»-Te) "

Сравнивая кпд для цикла Дизеля при постоянных и переменных теплоемкостях, например, при 6=15, (>=3 и начальном состоянии воздуха 1 atm и 300° К. аналогично получаем: при с= Const, η,= 0,567; при c + Const, у,=0,503.

Сравнение кпд циклов в тепловой диаграмме.

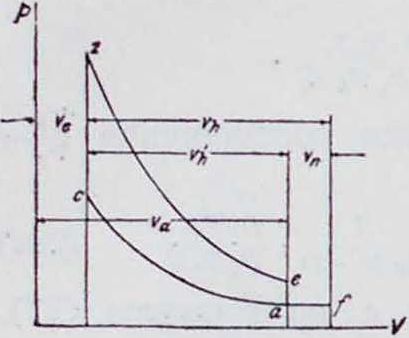
Весьма наглядное представление об использовании тепла в теоретич. циклах дает тепловая диаграмма. С повышением степени сжатия кпд увеличивается, что видно из фигура 15, где площадь acze соответствует полученной работе при данной степени сжатия. С повышением степени сжатия и, соответственно, температуры сжатия до точки с весь избыток тепла cc’zz, дополнительно введенный в рабочий цикл, идет на совершение работы. Теоретические циклы, ограниченные двумя адиабатами и изоплерой отдачи тепла, при разных способах подвода тепла по р =

= Const, t)=Const, T’=Const, дают разные тепловые эффекты. в зависимости от параметров. За основной исходный параметр м. б. взяты либо постоянная степень сжатия либо максимальное давление. На фигуре 16 представлены три

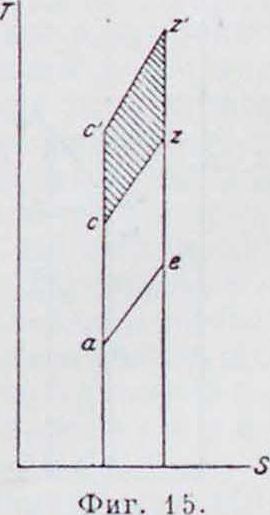
рабочих цикла с постоянной степенью сжатия, при условии, что количество тепла, отданное холодному источнику, для всех трех циклов постоянно. Наибольшему количеству тепла, обращенному в работу, равную площади acz_ve, соответствует сгорание ног>== Const, затем идет сгорание по р=Const,

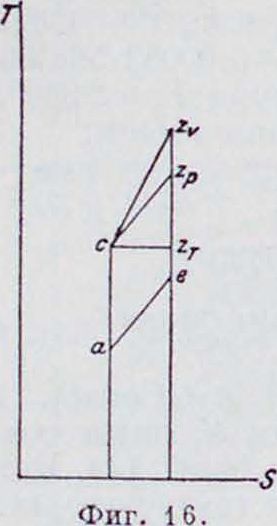
соответствуя площади acz_pe, и, наконец, наименьшее использование тепла дает сгорание по T=Const (площадь aczjS).

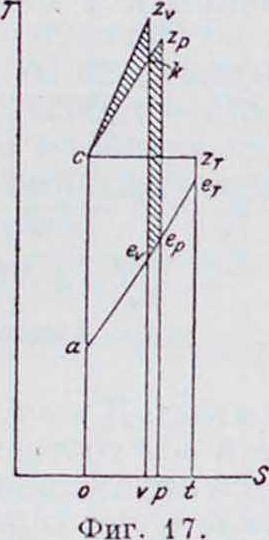
Такое же сравнение этих циклов можно произвести в предположении, что работа при всех трех формах сгорания получится одинаковая. На фигуре 17 площадь acz_ce_v соответствует теплу, обращенному в работу при сгорании по v — Const; при этом холодному источнику отдано тепло, соответствующее площади οαε,ν. Чтобы получить ту же рабочую площадь по р=Const, необходимо увеличить энтропию настолько, чтобы площадь cz_rk=kz_pe_pe_v; при этом количество тепла, к-рое отдано холодному источнику, будет на площадь ve_ve_pp больше, чем при сгорании по v—Const, а следовательно и термическое использование соответственно упадет. При сгорании по T=Const холодному источнику будет отдано тепло, соответствующее площади oae_Tt—большее, чем в предыдущих случаях при получении той же работы. Если сравнивать циклы при одинаковом максимальном давлении, предполагая, что количество тепла, отданное холодному источнику, для всех трех рабочих циклов одинаково, то наибольшее количество тепла, обращенного в работу, обеспечивает сгорание

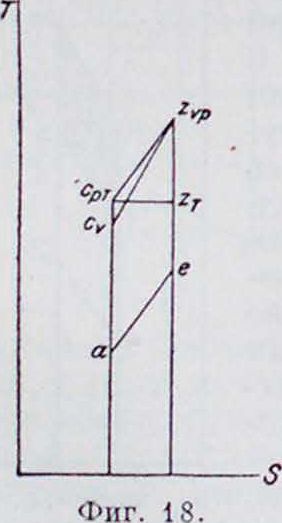
по p=Const, затем по y=Const, и наихудший результат дает сгорание но 7=Const, что видно из фигура 18. Такое же сравнение можно произвести в предположении посто янства количества тепла, обращенного в работу, причем результаты получатся те лее.

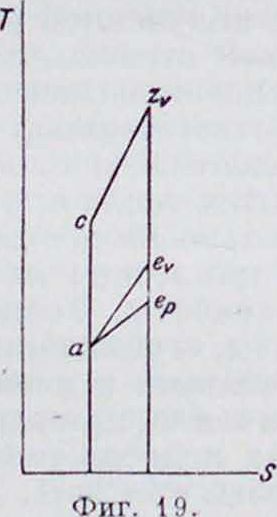
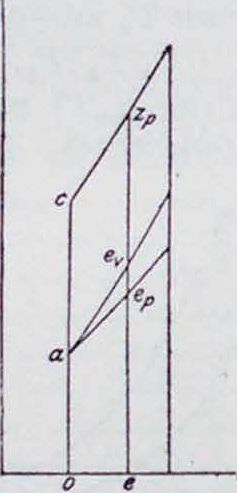
Сравнивая цикл Отто с циклом Гемфри, то есть с продолженным расширением, видим, что за счет продолженного расширения получается излишек рабочей площади ие,е_р. при той же затрате тепла (фигура 19). При сравнении нормального цикла Дизеля с циклом Дизеля, работающим с продолженным расширением, получается излишек площади ае_ге_р, за счет продолженного расширения при той же затрате тепла, соответствующей площади ocz_pe (фигура 20). Кпд цикла, ограниченного двумя изобарами, как видно из диаграммы, не зависит от нагрузки машины. Кроме того, из этой диаграммы видно, что выгодность продолженного расширения увеличивается с ростом нагрузки двигателя.

При сравнении использования тепла по смешанному циклу (фигура 21), у которого сгорание от точки с идет сначала по t>=Const до точки г,, а затем по р=Const до точки г,, с циклом Дизеля со сгоранием полиции cz_p. в предположении, что оба цикла должны дать одинаковую рабочую площадь,—энтропия для цикла Дизеля должна быть увеличена настолько, чтобы площадь cz_vz„k получилась равной площади ekz_pe при этом количество тепла, отданное холодному источнику по смешанному циклу, эквивалентное площади оаер, меньше количества тепла при сгорании по p=Const (площадь оаср).

Фигура 20.

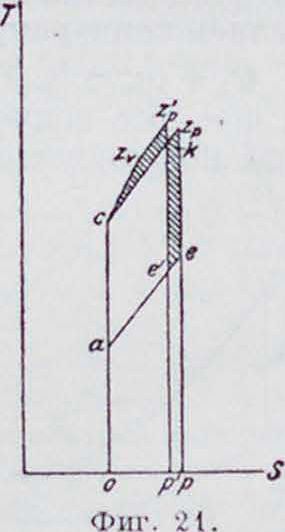
Аналогичные сравнения можно было бы произвести в тепловых диаграммах в предположении переменных теплоемкостей, и конечные результаты получились бы те же.

Действительные рабочие циклы двигателей внутреннего сгорания. Основные э л е-менты процесса всасывания. Когда кончается выталкивание сгоревших газов, в пространстве сжатия остается часть их с давлением, несколько ббльшим атмосферного. При обратном ходе поршня давление остаточных газов начинает понижаться до атмосферного; затем падение давления продолжается, и начинается всасывание свежей смеси, продолжающееся до тех пор, пока поршень не придет в другую мертвую точку а (фигура 22). Весь объём цилиндра V„ мы, однако, не в состоянии заполнить свежей смесью, в виду освобождения поршнем лишь рабочего объёма цилиндра V/, частичного заполнения цилиндра остаточными газами и сопротивления впускных органов. Назовем весовое отношение всосанного количества рабочей смеси к теоре-

тически возможному, отнесенному к объёму V_h в условиях работы, к о э ф ф и ц центом подачи >/„. Следовательно, если объём V_hпри давлении р₀ и темп-ре Т₀ окружающей среды будет заполнен целиком, то η„=1. Обозначим весовое количество остаточных газов через G_r, количество свежепосту-пившей смеси—через G₀ и количество газов в точке а—через G„. П редполагая, что в период всасы-

. -С - i___вания не происходит

_^РГ ρ д· ^а “ нагрева рабочей сме-

ф си от горячих дета лей, а имеет место только теплообмен между остаточными газами и свсжепоступившей смесью, молено написать следующие уравнения:

G_r(T_r — Т„) с=G₀ (Т_а— Т„) с",

G₀ + G_r=G_a.

Предполагая, что теплоемкости сгоревших газов е и свежепоступившей смеси с" мало отличаются друг от друга, и сокращая на это значение, получим после открытия скобок и соединения членов,- содержащих Т_а:

Т_а (G_r + G₀)=G_rT_r + G„T„. (26)

Заменяя соответствующие веса из характеристических ур-ий:

G_a —

Ра V_a. _r PrVr

Ра Та ’ ^г Рг Тг

_r _ „ P.Vk °° ^ίτ Р.Т.

подставляя эти значения в ур-ие (26) и предполагая равенство характеристнч. постоянных, получаем после сокращения:

РаУа P_rVr + VrPoV_h,

откуда

PnV„ - P_rVr P.Vh

или, разделив числитель и знаменатель на V_r и приняв во внимание, что ^=е (сте-

. V* V„ - Vr. ^т

пень сжатия) и _γ=_у =8 — 1, получим:

η, в G^pa ~Р_Г)· (²~)

Вводя в скобки выражение Р_а — Р_а, преобразуем данное ур-ие в

По=>_ί(Λ 1) (^еР« - ^Р« + ^Р« “ ^рг) =

Ра (^а — 1) + Рд — Рг Ра (Рг Ра * /OQ 1) Р. р. pj*~!*·

то есть если смесь в процессе всасывания не нагревается о горячие стенки рабочих органов, то коэфф. подачи не зависит от темп-ры остаточных газов, а зависит лишь от относительного разрежения во время всасывания, относительного сопротивления во время выхлопа и от степени сжатия. С повышением степени сжатия коэфф. подачи растет, с увеличением сопротивления во время всасывания и выталкивания он падает. Назовем коэфф-том остаточных газов у отношение весового количества остаточных газов к весовому количеству свежезасосанной смеси:

Так как

G, =

PrVr Rr fr ^:

a G₀=v_r

P,Vh

R.T.

У =

P_rV_rR,T

RrTrPVh

R₀=R_r и вводя получаем:

туг.

1

Считая - *-1,

^ PytvTr (* - 1) ~ )г (« -

Подставляя значение η_νРгТ.

V»

соотношение _у

РгТ. РЛг получаем:

(29а)

из формулы (27), (296)

Tr(tPa-Pr)

Температура смеси в точке а начала сжатия определяется из формулы G₀+G_r=G_a: G_a=G„ + G,.=Go + yG₀=Go (1 + у),

РaVа __ PgVh Vo (1 · >’)

PaT a PoG

Полагая R₀=R_a, находим:

PnV„T.

T —

I Vh (1 +-/)

Подставляя из ф-лы (27) и (29б) η_νγ дя соотношение ~ ¹, получаем:

сР„Т,

еР_а-Рг

Т.

и вво-

(30)

Гг

г	(РгТа
и	г.гг	pj

Как видим, три основные величины процесса всасывания: >/„, у и Т_а определяются через давления всасывания и выхлопа, условия окружающей среды и температуру остаточных газов.

Если предположить, что смесь в процессе всасывания нагревается о горячие стенки рабочих деталей, то коэффициент подачи будет зависеть, кроме вышеуказанных факторов, также и от относительной величины подогрева и выражается формулой:

(31)

Имея диаграмму, снятую слабой пружиной и дающую 1 и Р„, зная условия окружающей среды и задаваясь темп-рой остаточных газов, можем определить температуру Т„ по формуле (30). Затем, учитывая подогрев от стенок и поршня некоторым повышением температуры Т_а и подставляя в формулу (31) Т_а — Гά+ ΥΓопределяем коэффициент подачи η,. Имея последнюю величину, по формуле (29а) вычисляем коэфф. остаточных газов у. Величину УГ_а можно брать в пределах 10—25°. Обратно, если имеется коэфф. подачи исполненных машин в зависимости от конструкции распределительных органов и сопротивлений всасывания и выталкивания, определяем Т_а начала рабочего процесса и у.

Заполнение рабочей смесью цилиндра двухтактных Д. в с. В двухтактных двигателях процесс заполнения цилиндра свежей смесью производится за счет работы особого продувочного насоса (для мелких двигателей используется кривошипная камера), сжимающего рабочую смесь до давления на 0,15—0,35 atm выше давления окружающего воздуха. Теоретически в точке е по прямой еа (фигура 23) производится выхлоп газа, после чего через орган, управляющий продувкой, в цилиндр поступает сжатая продувочным насосом рабочая смесь (или воздух) по линии af—fa и вытесняет через выхлопной орган продукты сгорания. Сжатие начинается с точки а. в которой закрываются все органы распределения. При выхлопе через щели, управляемые поршнем, точки е и а лежат на одной вертикали диаграммы. Тачан·. 23. ким образом из всего рабочего объёма F/, теряется объём V, и используется объём Г(.

Обозначая степень сжатия с=видим из чертежа, что из геометр, размеров цилиндра машины м. б. введено второе соотношение

«= ]/. исчисленное по отношению ко всему v_c-

ходу. Цикл и отдельные процессы его, естественно, должны подсчитываться по величине в=л Связь между этими двумя ве-

V Г

личинами определяется следующим образом: _c_^v_a_vi+v_c

V ^{Vc Vc}

Обозначая через λ (доля потерянного хода), получаем:

ε=(i — 1) (1 — /.) + 1=As,

гТТР

4 ₌ C-i)(i-3) + i.

fi

Коэфф-т подачи, отнесенный к объёму Ту,

(1 — V>)4 JfcVx- (1-у)/П>

^Vv V,;* Vik(l-A) * где ψ—коэффициент утечки, V_k и η_)ι—рабочий объём и коэффициент подачи компрессора. Коэффициент остаточных газов у определяем по формуле:

7 =

РАа - РечЛл

Начальная темп-pa сжатия Т_а определяется по формуле:

Т„ =

Гг

ΊνΡо(^г - 1) IT

8N

(33)

Период с я: а т и я. В идеальном случае сжатие должно протекать по адиабате с переменным показателем. В действительном же процессе происходит потеря тепла, и сжатие идет приблизительно по некоторой политропической кривой с постоянным показателем 1,35, отличающимся от показателя адиабаты. Можно принять показатель линии сжатия соответствующим политропич. кривой с постоянными теплоемкостями, и как основные элементы, влияющие на величину этого показателя, следует признать размер машины и скорость рабочего поршня. Чем больше объём цилиндра, тем меньше относительная площадь охлаждения; чем машина быстроходнее, тем меньше время соприкосновения рабочего тела с холодной стенкой.

Оба эти фактора повышают показатель политропы. Для двигателей Дизеля, работающих с большой степенью сжатия, указанное явление протекает в том же порядке. Для двигателей, работающих с калоризатором, явление подогрева в конце сжатия идет еще более интенсивно. Практически показатель политропы линии сжатия колеблется для нормально исполненных моделей от 1,3 до 1,35, достигая иногда и больших значений (до 1,4). Вообще же следует отметить, что влияние показателя политропы па развитие рабочей диаграммы весьма незначительно, что видно будет из последующего. Впрыск воды в процессе сжатия для понижения температуры, конечно, уменьшает показатель, и для простых нефтяных двигателей, работающих с впрыском воды, он колеблется от 1,2 до 1,25 за счет испарения воды.

Период crop а н и я. Обычно в Д. в с. введенное топливо не успевает сгореть за время видимого сгорания и частью догорает на линии расширения. Чтобы разобраться в истинной причине явления догорания, необходимо рассмотреть те условия, которые обеспечивают полноту сгорания и лучшее использование тепла. Как было уже указано, лучшее тенлоиспользование может быть достигнуто сгоранием по линии постоянного объёма, для чего нужно сжечь все топливо в мертвой точке. Точное выполнение этого требования не может быть достигнуто, так как для сгорания требуется определенное время. Скорость же сгорания, по новейшим исследованиям, зависит от состава рабочей смеси, то есть от коэффициента а, от хорошего ее перемешивания и гл. обр. от тех вихревых движений, которые вызваны в рабочей смеси, в меньшей степени—от темп-ры и давления в начале сгорания. Скорость сгорания различных смесей неодинакова. Опыты Клерка (фигура 24) вполне подтверждают это положение. Клерк производил свои опыты в цилиндре с диаметром <1=180 .и.м и ходом поршня s=250 миллиметров. Самопишущий прибор дал кривые, изображенные на фигуре 24.

qas Оуо His Нго Цм Hw Hsc at.

Фигура 24.

Кривая а соответствует смеси газа и воздуха в объёмных долях

» Ь »

» с »

» d >

*> e »

„

.) д ,>

» h »

л i »

Эти кривые скорости сгорания даны в зависимости от коэфф-та смешения. Как видно, скорость сгорания повышается с переходом от бедных смесей к богатым, достигая

1 : 13

1 : 12 1 : И 1 : » 1 : 7 1 : 6 1 : 5 1 : 4

своего максимума. Дальнейшее обогащение смеси понижает скорость сгорания. Так, при коэффициенте смешения непродолжительность сгорания равна 0,05 секунды, тогда как при коэффициенте смешения 1:14 она в 10 раз больше (0,5 секунды) и при коэффициенте смешения 1:4 достигает 0,15 сек. Скорость сгорания зависит также от давлении сжатия, под которым протекает сгорание. Те же опыты Клерка иллюстрируют это положение (табл. 0).

Таблица 6.—Скорость сгорания по опытам Клерка (при скорости поршня «=5 м,ск).

Виды смеси	Скорость сгорания в м/ск
	при сжатии Оез сжатия р _ 2,5 aim
Богатая. Бедная.	22 18 7 6,25 1

Зависимость скорости сгорания от t° всасывания для светильного и генераторного газов, по опытам Негеля, характеризуется табл. 7; из нее видно, что повышение ί° оказывает положительное влияние на скорость сгорания. Итак, хотя нагревание во время всасывания и сжатия способствует лучшему перемешиванию газов, по повышающееся вместе с тем давление мешает газам хорошо диффундировать.

Таблица 7.— Зависимость скорости сгорания от t° всасывания.

Наименование и	Скорость сгорании в м ск
состав смеси
	при 15	при 75°
Светильный газ 1С%	3.5	3.8
Генераторн. ·» 46.5%	1,95	2,1

На диаграмме (фигура 25) приведены скорости сгорания бензиновых и овых смесей, в зависимости от избытка воздуха а в двигателе «Скрипе», по опытам Лаборатории Д. в с. Московского высшего технич. училища. Как видно из диаграммы, максимальная скорость сгорания для таких топлив получается для a е“ 0,9 и достигает для бензина 22 м/ск. Как с обеднением, так и с обогащением смеси скорость сгорания сильно падает.Если сравнивать численные значения скорости сгорания, полученные Клерком, Негелем и лабораторией Московск. высшего технического училища, бросается в глаза их несоответствие: Клерком и лабораторией МВТУ получено число 22, а Негелем — 3 м/ск. Это объясняется тем, что Клерк и лаборатория производили свои опыты па работающем двигателе, тогда как Негель—в х. Если предположить, чтов закрытой бомбе газ с воздухом хорошо диффундировали в однородную смесь, то опыты Негеля дают действительную скорость сгорания, когда смесь находится в покое. Эти скорости недостаточны для того, чтобы закончить сгорание даже за один рабочий ход: так, например, для автомобильного двигателя, делающего 1 800 об/м., рабочий ход (сгорание и расширение) совершается в =

¹ сек.; при ходе поршня равном 100 миллиметров и скорости сгорания в 3 м/ск сгорание заканчивалось бы в начале всасывания. В действительных рабочих диаграммах, однако, мы видим, что двигатели развивают нормальную рабочую диаграмму с небольшими отклонениями от r=Const, соответствующую скорости сгорания 20-1-30 м/ск, в зависимости от числа оборотов машины. С повышением числа оборотов увеличивается скорость вихревых потоков в рабочем цилиндре и очаг сгорания быстро переносится на всю рабочую смесь, так как вихревые скорости значительно превосходят скорости распространения волны сгорания в покоящейся смеси.

Коэффициент выделения тепла. В связи со всеми перечисленными выше влияниями на линию сгорания, из располагаемого тепла лишь часть будет обращена в полезное давление для двигателя Отто и в соответствующее увеличение объёма для двигателя Дизеля. Остальная часть пойдет в охлаждающую воду; часть топлива совершенно не горит, характеризуя неполноту сгорания; часть же топлива горит в процессе расширения, и некоторое влияние на теоретические давление и объём окажет также диссоциация. Назовем долю от введенного тепла, получаемую как полезное тепло в процессе видимого сгорания, коэффицентом выделения тепла с. Тогда, при сжигании единицы количества топлива с теплотворной способностью II_и, количество тепла, которое выделится в процесс видимого сгорания, будет Ш„. Значение I зависит от конструкции машины, очертаний камеры сгорания, однородности смеси или способа распылива-ния топлива и от числа оборотов машины: с повышением степени сжатия убывают потери в охлаждающую воду; совершенство диффузии и распиливания влечет за собой полноту сгорания; увеличение числа оборотов уменьшает теплоотдачу в стенки, но увеличивает фактор догорания. Практически для хорошо исполненных моделей коэффициент выделения тепла с колеблется в пределах от 0,75 до 0,95. Малое значение коэфф. I явно указывает на догорание в процессе расширения, и при выборе значений для ξ необходимо их связывать с соответствующим значением показателя политропы расширения п_г: чем меньше I, тем меньше и Вообще следует отметить, что в большинстве двигателей может иметь место догорание за весь процесс расширения, и недовыделивше-еся в процесс видимого сгорания тепло отчасти используется в процессе расширения. Значение коэфф. выделения тепла £ для разных типов двигателей можно для предварительного теплового расчета брать по табл. 8.

			А	HMJ
1			J
!
		h	/сп	ирп	j		X
		А			N
		у						V-
it
	7
L		Изб	ь/т	*	ojO	xo	:

οχ 0,7 ца на г,о μ χ г,з г,а Фиг“ 25.

Т а 0 л. 8.— Значения коэффициента выделения тепла {.

Двигатели Дизеля..0,82—0.92

Нефтяные двигатели..0,75—0,85

Газовые двигатели..0,80—0.88

Быстроходные автомобили и авиационные двигатели0,80—0,97

Период расширения. Теоретически, адиабата линии расширения идет с переменным показателем, увеличивающимся по мере расширения газов в пределах от 1,25 до 1,32, в зависимости от нагрузки. В виду теплоотдачи в стенки кривая расширения должна идти круче адиабаты и с большим показателем против нее. В свою очередь, догорание компенсирует потерю на охлаждение, приближая действительную линию расширения к адиабатич. кривой. Практически при построении рабочей диаграммы принято считать линию расширения идущей с постоянным показателем, что, однако, не соответствует действительному рабочему процессу, но дает значительное упрощение при сравнительно небольших неточностях.

Для хорошо исполненных моделей п_г колеблется в пределах 1,284-1,35, в зависимости от выбора коэффициента £, но может в неудачно исполненных моделях упасть даже до 1. По опытам Герберга, показатель линии расширения зависит гл. обр. от давления «катая, что видно из след, сопоставления:

При давлении сжатия Рс В atm. 16 10 8 6 4 3

Показатель линии расширения п,. 1,285 1,295 1,365 1,385 1,395 1,43,

то есть с повышением сжатия показатель линии расширения падает. На показатель влияет, хотя не в сильной степени, и величина нагрузки. Герберг производил опыты при разных нагрузках, от больших до холостого хода, и нашел, что показатель при этом менялся в пределах 1,284-ί,33; для холостого хода он был равен 1,38. Такая зависимость показателя п„ от нагрузки понятна: с уменьшением нагрузки уменьшается и количество рабочей смеси, поверхность же охлаждения остается одна и та же, так что, несмотря на понижение температуры относительная теплоотдача как бы увеличивается, и показатель возрастает. На величину показателя линии расширения влияет также и число оборотов двигателя: чем оно больше, тем короче время соприкосновения газов со стенками в период расширения, а значит и теплоотдача в этот период меньше; следовательно, показатель п_г уменьшается. Эту зависимость подтверждает и Клерк, который нашел колебания п_г для разных чисел оборотов в пределах от 1,2 до 1,43. Впрыскивание воды в цилиндр тоже влияет на уменьшение показателя п_г. Часть тепла тратится на испарение впрыскиваемой воды, темп-ра понижается, и уменьшается теплоотдача во внешнюю среду, что и вызывает понижение п_г до 1,2; иногда оно доходит даже до 1. Это бывает при перегрузках, когда часть смеси не успевает сгорать, и по линии расширения происходит сильное догорание.

Продув к а двухтактных двигателей. В двигателях внутреннего сгорания, в частности—в двухтактных, давление сгоревших газов в конце расширения равно 24-5 aim. В момент открытия выхлопных окон сгоревшие газы с постоянной скоростью, равной скорости звуковой волны (соответственно показателю к и температуре), устремляются через выхлопные окна в атмосферу, причем с понижением давления в цилиндре ниже критического скорость истечения будет постепенно падать. Обозначим давление внутри цилиндра через р_;, давление в выхлопном трубопроводе—через р„; тогда с падением давления в цилиндре наступает критическое отношение давлений:

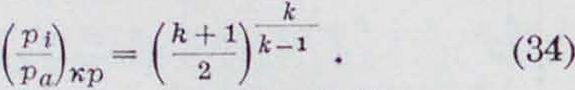
Для двухатомных газов (к=1,4) это отношение равно 1,89.

Если начальное давление в цилиндре больше давления, соответствующего критическому значению, то есть

Ро > (* 1¹)·~ ¹ Ра,

то секундный вытекающий вес в килограммах определяется из выражения

Gck= Wmojc j/"" ζ >

где f—площадь поперечного сечения окон, μ—коэфф. истечения, а у>_тах—постоянная величина, не зависящая от начальн. давления:

	Ψτηαχ- (k’+l	ι*ν.·:Ί
Если
	Ро < ( к
ТО
	II К о о
где
Ψ =	1/W,	®L(S

(35

(36)

и, следовательно, количество вмтекающ. газа зависит от постоянно падающего отношения давлений —. Т. о., за время dt вытекает

Ра

dG=μψί у I)

dl.

(37)

Предполагая, что процесс идет по закону политропы (с показателем m= 1,254-1,35), и обозначая через р₀ и v₀ давление и уд. объём в начале рассматриваемого процесса, при р; и υ_{, меняющихся по времени, имеем:

р= РоЧ>^т.

vi _ pi (vi ^m _ Го (т »»_t

Vf 1о Ро) ν* Ро)

откуда

dG= w/О ² ""dt. (38)

После соответствующих подстановок и интегрирования получаем время-сечение для выхлопа и продувки:

^{J т} “ I г»¹»

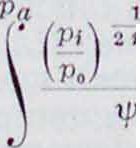
; - ^d Ю · <³⁹⁾

где V—объём цилиндра в процессе выхлопа и продувки—принимается постоянным.

Очищение цилиндра от сгоревших газов идет но трем законам истечения (фигура 20). 1) В момент, когда выхлопные окна открываются (точка е), устанавливается критическая постоянная скорость истечения вплоть до критич. давления (точка /с), и ко-эфф. у в этот период истечения (кривая ек) принимает постоянное значение 4>тах Для среднего состава продуктов сгорания, при/с 1,3, V’max⁼2,09. 2) За-

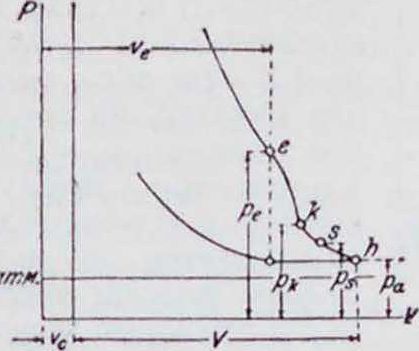
Фигура 26. тем, начиная скри-

тическ. давления,в пределах низких давлений истечения (участок ks) скорости вытекания постепенно надают в зависимости от падения давления в цилиндре. 3)В тот момент, когда давление в цилиндре упадет до давления в ресивере или в продувочно-кривошипной камере р, (точка s), открываются продувочные окна, и сгоревшие газы в цилиндре, с одной стороны, вытесняемые продувочным воздухом, ас другой—под влиянием разности давлений в цилиндре и выхлопном трубопроводе выталкиваются через выхлопн. окна. Для первого периода получаем для определения время-сечения до критич. давления след, ф-лу:

V

Г/dt - 0,717, ,. (0,932 p/^m- 1). (40)

у 1 й

Аналитич. решение интеграла для второго периода (выхлоп ниже критич. скорости), для области низких давлений, в виду переменности у невозможно, и решать его приходится графически, в результате чего необходимое время-сечение берется по формуле:

tfc tg

Jfdt + jfdt =

- 0,173 t~=f [(3,86 + Z.) Ve°"“ - 4,14], (41)

У ¹ e

Pa

pi

берется no

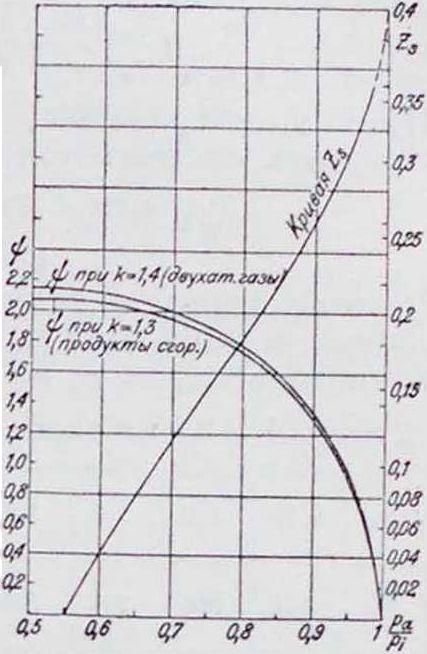
где Z„, в зависимости от графику (фигура 27).

Период продувки. В момент открытия продувочных окон давление в цилиндре равно давлению в ресивере p_s, и продувка цилиндра идет от продувочных окон к выхлопным, преодолевая сопротивление обоих этих окон. В виду того, что выхлопные окна в начале продувки имеют значительно большее сечение против продувочных, уравнивание давлений в цилиндре пойдет быстрее, чем подача свежего воздуха в рабочий цилиндр через продувочные окна. Предполагая для всего процесса продувки постоянное давление в ресивере р„ определим необходимое вре.чя-сечеиие продувочных окон. Количество воздуха, вытекающего за время dt:

μνί}/~5* dt; fdt*= ^dG

dG

f f dt

Ί

Ps

(42)

PV-f

Ps

Это выражение содержит два неизвестных:

1) время-сечение J f dt, 2) величину у, зависящую от давления р_г в цилиндре. Для щелевой продувки, задаваясь началом открытия выхлопных окон и определяя начало открытия продувочных окон, тем самым получаем время-сечение для продувки и для всего выхлопа. Определение время-сечения для продувки и выхлопа произведем графически, зная диаметр и ход поршня и отношение длины шатуна к радиусу кривошипа. Для этой цели построим кривую зависимости хода поршня от угла поворота кривошипа с момента

ОТКРЫТИЯ ВЫХЛОП- Фигура 27.

пых щелей (фигура 28).

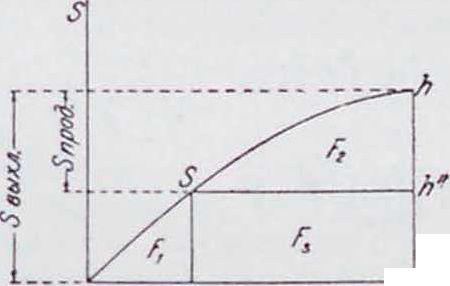
По оси абсцисс откладываем угол поворота кривошипа а, а по оси ординат—соответствующий ему ход поршня s (от начала открытия выхлопных щелей), построенный по точкам. Полученная интегральная площадь ohh разбивается на 3 площади: F₂ и F₃,

где К, соответствует время-сечению предварения выхлопа до уравнивания давления с ресивером, 2(F₃+F₃)—время-сечению выхлопа за период продувки (учитывая обратный ход поршня), 2F₃—время-сечению продувки. Определяя масштабы диаграмм, находим необходимое время-сечение продувки по указанной площади. Из уравнения (42) определяем значение у:

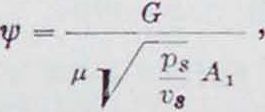
(43)

где Α, — Sfdt (время-сечение продувки). В этой формуле по фигура 28 известно время-сечение, состояние продувочн. воздуха в ресивере и его количество, которое для машин с отдельным продувочн. насосом берется —jp-ciftcAj ^с избытком в _Фиг 28 35—80% против рабочего объёма цилиндра: у=1,35 — 1,80. У двигателя с кривошипно-камерной продувкой φ равно 0,8 ; 0,6. Таким образом, имеем:

но:

T₀v«o=«,(yj”¹;

G=-^V” · (44)

-КГ

Принимая показатель сжатия в компрессоре

η=1,3, получаем следующее значение G:

г, νφ /ТЛЗ.гз

^с=гг1т₈) ·

Подставляя в ур-ие (43), находим:

_V=-L. -^V*_, (^ ³·³³= —. _£=(^Τ-»Υ·³³.(45)

Λ, μ yp,v, T_a) A, ^l/HT, T_s ⁴ Принимая T₀=2S8°, /<=0,825 и 11=29,2, получаем окончательно:

0,224 νφ /288 3,33

У> ⁼ — (46)

Ai У Ό T_s-

В этой формуле температура Т, определяется в зависимости от давления продувочного воздуха p_s по табл. 9.

Т а 0 л. 9.— 3 а в и с и м о с т ь между p_s и T_s.

Ps	1,15	1,2	1,3	1,4	1,5	1,6	1,7	1,8
Ts	301	305	314	323	331	339	347	354

Определив ψ из формулы (46), находим по фигура27 соответствующее отношение давлений

^Р: (при fc=1,4 для воздуха), а по заданно-

Ps

му p_s—величину р.

Теперь можно проверить, достаточно ли располагаемое время-сечение для выхлопа в период продувки двигателя при известном отношении давления цилиндра р. к давлению в выхлопном трубопроводе р„. На основании предыдущих рассуждений можно написать аналогичное выражение и для конца выхлопа, то есть предполагая, что выхлоп идет при отношении давления р„ к р. в цилиндре; при этом время-сечение выхлопных окон, соответствующее площади 2(F«+F₃), не должен быть меньше необходимого при указанном отношении давлений, то есть

Sf^di> =

^μψν

(47)

Подставляя вместо G его значение G= _τ φ, получим:

dt^ ^V-~—, или J f dt >

но

μψ

1 i: Vi

при m=1,3,

/n ⁰·²³¹

или, принимая μ=0,825, 11= 29,2:

(48)

1/"»°,««,^®)·”·. <⁴⁹> Здесь ψ берется по фигура 27 для отношения давлений ^Ра и /с=1,3; все остальные вели-

чины известны. Если это условие будет удовлетворено, то выхлопные окна будут достаточны. В случае же, если время-сечение для выхлопа в период продувки получится с большим избытком против необходимого по формуле (49), нужно пересчитать продувку, задаваясь новым моментом открытия выхлонн. окон. В случае кривошипно-камерной про дувки давление продувки p_s доля-сно оыть при пято как среднее значение изменения давле пия от начала до конца продувки. Практиче

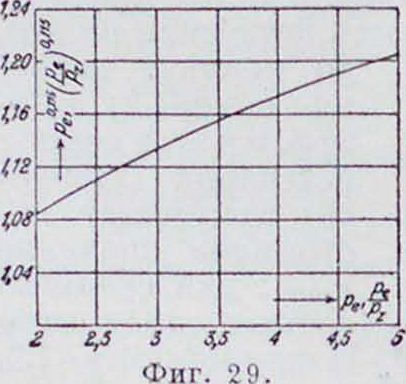
фициента φ в этом слу 11а диаграмме фигура 29

скн, при максимальном давлении продувочного воздуха в кривошипной камере 1,3 atm абс., расчет ведется на среднее значение р_а=1,2. Количество продувочного воздуха подсчитывается по ко-эфф-ту подачи насоса, и значение коэф-чае меньше единицы, дана кривая значе ний р_е^0,115 п в формулах (41), (49).

Теплоиспользование в двигателях внутреннего сгорания. Тепловой баланс. В идеальной машине из располагаемого тепла Q_y передается холодному источнику количество тепла Q₌ и используется только часть тепла, равная Qi — Q* (фигура 30). Это использование тепла соответствует термическому кпд В действительной машине вследствие охлаждения двигателя водой большинство потерь относятся за счет тепла, подлеясащего отдаче холодному источнику, и лишь часть тепла уходит в воду за счет воз-можного термическ. использования. Потерю тепла в действительной машине, соответствующую потере тепла Q., в идеальной машине. можно разбить на три основные потерн: 1) в охлаждающую воду, 2) в окружающую среду и 3) с отходящими газами. Кроме этих потерь, в действительном двигателе

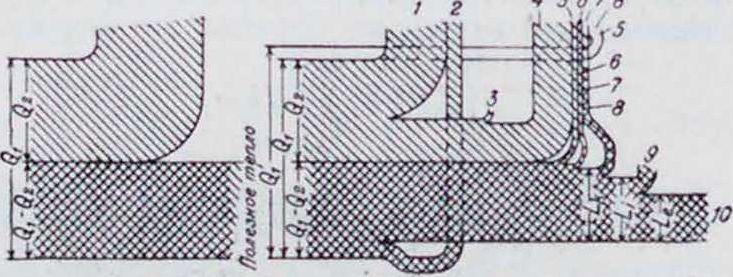
Фигура 30. Тепловой баланс. Потерн: 1—в охлаждающую иоду, 2— часть потерь от трепни. несовершенства горения и работы насосов и компрессоров, отходящая с охлаждающей водой, л—от лучеиспускания, 4—с выхлопными газами. 5—от замедленной вспышки,#—от догорании. 7— на работу насосов, к— от неполноты горения, а — от работы трения.

10— Полезная работа двигателя. имеются еще следующие потери: 4) от ра боты трения поршня, отдающей тепло через стенки цилиндра в охлаждающую воду, 5) от замедленной вспышки, 6) от догорания, 7) па работу насосов, 8) от неполноты горения н 9) от работы трения. Остающаяся часть тепла обращается в полезную эффективную работу двигателя.

Коэфф-ты полезного действия. В зависимости от распределения тепла в двигателе отличают следующие кпд:

1) Термическим кпд ?,·, называется отношение тепла (AL,), обращенного в работу, к затраченному теплу Q_l в идеальной машине, то есть работающей без потерь. Вычисление его приведено было выше.

2) Отношение тепла, соответствующего действительной работе газов в цилиндре,

при учете действительных потерь в рабочем цикле (индикаторная работа L,), ко всему затраченному теплу называется индикаторным кпд

3) Отношение индикаторного кпд к термическому называется относительным кпд,

или степенью использования: v_n==i¹ ·

Vt Lt

Этот коэфф-т учитывает т. о. потери работы газов действительной машины по отношению к идеальной.

4) Работе L,· газов противодействует трение дигателя L_r, и действительная работа, полученная на валу машины, L_f=L_: — L_r. Отношение количества тепла, обращенного в действительную работу на валу машины, к затраченному теплу называется действительным, или эффективным, кпд η₍.

5) Отношение эффективного кпд, или эффективной работы, к индикаторному кпд, или индикаторной работе, называется механическим кпд: η„.=—=^Lr.

^m vi и

Так.обр., механический кпд характеризует относительную работу трения механизма. Итак, связь между указанными кпд, характеризующими рабочий процесс действительной машины, следующая:

Ve=Vt Vm=Vt Vg Vm

Влияние с T e п e н и с ж а т и я и состав а смеси на баланс тепла. Таблица 10 дает на примере генераторного газа (α= 1,5) распределение тепла (в %), в зависимости от степени сжатия t.

Та 0 л. 10. — Распределение тепла в % в зависимости от степени сжатия е.

е	Яе	Я to	чя	Остаток
з.ез	21,5	50.4	22.7	5.4
4.58	24.0	49.9	21.6	4.5
6,58	27.9	48.5	18.3	5.3
8.16	29.3	45,6	19.3	5.8

Как видно из нее, чем больше е, то есть чем больше давление сжатия, тем больше тепла обращается в полезную работу ((/,.). Потеря тепла в воду (q,_r) с увеличением <- несколько убывает, так же как и потеря в выхлопах {(],). Остаточный член, включающий потерю от неполноты сгорания и в окружающую ^сР^еДУ.остается почти без изменения, что указывает на достаточную точность приведенных опытов. Таблица 11 показывает, что максимум работы двигателя получается при вполне определенном составе рабочей смеси и что при уклонении в ту пли другую сторону от этой величины полезная работа убывает.

Таблица II.—Р а определение тепла η за-вис и мости от и о э фψици опта из бы т к а воздуха « (е= 8.16).

а	Чс	Я w	Чд	Остаток
1.33	27,8	48.3	17.2	6.4
1.56	29.1	45.9	18.6	6.4
1,88	30,6	41.1	20.4	7.9
2.21	30.4	37,1	22.4	10.1
2 58	29. G	36,1	25,1	9,2

Т.о.,длл наиболее выгодного использования тепла в двигателе необходим определенный состав смеси, дающий наиболее полное сгорание. Вопрос об удачном подборе состава рабочей смеси особенно важен при выборе системы регулирования двигателя. Степень сжатия влияет на количество индикаторной работы двигателя (L,·), а следовательно, и па индикаторный кпд (?/,·)· Однако, с увеличением степени сжатия повышается одновременно и кпд идеальной машины (?/,), а также растет количество теоретически возможной работы (L,). Поэтому степень теплоисполь-зования определенного двигателя _ ^Ll Ή

⁹ Lt щ остается приблизительно постоянной. Таблица 12, составленная по опытам Негеля, иллюстрирует это.

Таблица 12.— Кпд двигателей в зависимости от давления сжатия.

Ре	V,	щ	vg
5.87	0.352	0.230	0.650
8.21	0.400	0.264	0.660
13.50	0.483	0,306	0.634
18.40	0,507	0.328	0.647

Повышение давления сжатия р,. с 5,87 до 18,4 atm дало повышение η_t от 0,35 до 0,50; индикаторный кпд, полученный непосредственно из опытов, поднялся с 0,230 до

0,328. Относительный же кпдг _д=остается приблизительно постоянным, колеблясь в пределах G4-4-GG %.

Расчет двигателя. Расчет по рабочему воздуху и среднему давле-н и ю. Расчет двигателя по заданной мощности сводится к определению рабочего объёма его цилиндров V_h, а по последнему — диаметра D и хода поршня S. Исходными параметрами, кроме мощности N_e и числа оборотов коленчатого вала в минуту, служит или количество рабочего воздуха, задаваемое на основании тех опытных данных, которые получены с двигателями данного типа, работающими на данном топливе, или среднее индикаторное давление рр, эта величина или выбирается опять-таки на основании опытных данных или определяется из теплового расчета, впервые предложенного проф. В. И. Гриневецким. Если двигатель работает на топливе с теплотворной способностью Н„ (в Cal на 1 .и³ газообразного топлива нормального состояния при 15° и 1 atm абс.) или h„ (в Cal на 1 килограмм жидкого топлива) и на 1 м³ его мы даем L м³ воздуха (при жидком топливе—на 1 килограмм—L м³ воздуха нормального состояния), то тепло, выделяемое всей рабочей смесыо при полном ее сгорании, будет

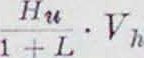
Принимая во внимание, что рабочая смесь, засосанная двигателем, будучи приведена к условиям окружающей среды, займет лишь часть рабочего цилиндра, мы должны в полученное выражение внести поправку на t° Т₀ и давление Р₀ окружающей среды и умножить его на коэфф-т подачи Получим:

288 Р„ Ни у

Т„ 10 000 1 + L ’ 1‘ Vt ·

Если двигатель дает п об/м., то для случаев т. Э. m. VI.

7

четырехтактного цикла это выражение надо умножить на ” (за два оборота—одни рабочий ход), а для двухтактного цикла—умножить на η. На основании этого мощность двигателя выразится:

я„

1 4* L·

288 Р„ 10 000 Т,

427

60-75 ^>ie ’

(50)

где i]_e—эффективный кпд двигателя. Отсюда рабочий объём в .и³

, _ 10000·2·60·75ιΥ_β(1 + L) Т, ^h ~ 288-427Huivlen Р,

Для четырехтактных двигателей:

V_h= 732

’ Л HuWen Для двухтактных двигателей:, Т. N,(1 + L) ₄

Hu’ivltn

V_h=366

(51)

(52)

Итак, если известен η₍ данного тина двигателей, то, задаваясь определенным S, можно из этих ф-л определить и Ώ. Из полученных формул можно было бы сделать вывод, что мощность четырехтактного двигателя при одних и тех же размерах и том же использовании вдвое меньше мощности двигателя двухтактного.

Основные размеры двигателя можно также подсчитать, зная из практики среднее эффективное давление для данного типа двигателей. По уравнению работы пишем для четырехтактного двигателя:

ту ₌ Р»Унп ₌

^е 2-60-75 _т7 9 000 N

⁼ Реп

PeVhn У 000 ’

(53)

(54)

Здесь N_e—в IP; Р_е—в кг/м²; двухтактного двигателя:

_ РcVhi} ^е 4 500 ’

V_h—в .и³. Для (55)

откуда

» ⁴,⁵⁰⁰Д

^h~ Р_еп-

Если V_h выражено в л, а р,. в для четырехтактного двигателя хт _ PeVhn _№

^{Λ _} 900 ""

для двухтактных двигателей

JP.

(56) кг/см², то

(57)

(58)

Обе выведенные ф-лы для определения основных размеров должны дать одни и те же результаты. Приравнивая ур-ие (51) и (54), можем написать:

~.м Т, N,(l + L) 9000Ne Pe Hu<v1en Pen

Заменяя здесь Р_е через Р,п_т и η_Γ через получим:

0,0813 I’

* о

(59)

откуда

0,0813 ^Т°

’ Ре

PM + L) Ни^г,Ю

(60)

Для ясидкого топлива, объёмом которого для стационарных двигателей обычно пренебре-1ают, получим:

V < =

0.0813 ^т°

Ро

PiL

hu.v

(61)

(где р; и р₀ в килограммах/см²). Из выведенных ф-л видно, что индикаторный кпд г_п зависит,

при прочих равных условиях, от среднего индикаторного давления р₍ и, чем оно больше, тем двигатель экономичнее. Из выражения для iji становится понятным влияние качественного и количественного регулирования на кпд двигателя: давая смеси больше воздуха, то есть увеличивая L, мы тем самым понижаем р,·; произведение же p,-(l+L) остается приблизительно постоянным, и ?/,- сохраняет свою величину. При количественном регулировании с изменением р,- меняется коэфф-т подачи у„, и отношение этих значений мало влияет на изменение индикаторного кпд. Это справедливо, конечно, если отвлечься от влияния регулирования на потери в рабочем цикле.

Расход топлива. Обозначая через С,- расход топлива на индикаторный сило-час в килограммах, имеем:

632

^V I Ни

(62)

(632 Cal—термический эквивалент силочаса). Приравнивая это выражение полученному выше, имеем:

Д²=0,0813 ^т° · ^Р1Ц ^L)

С Ни Р о Hu’iv

Отсюда для газообразного топлива:

р _ 7 780 р„»;_в

T.pt(l + L) ’

а для жидкого топлива (для стационарных двигателей):

(63)

гл ’ 7 780 Ро> н

ToViP

(64)

Следовательно, расход топлива тем меньше, чем больше p_t, и Гюльднер, повышая среднее индикаторное давление до 7 atm, значительно понижает этим расход топлива в своем двигателе.

Тепловой расчет (по Гриневецкому). Для определения размеров двигателя выше применялись практич. величины: или среднее эффективное давление или эффективный кпд (что равносильно расходу топлива на силочас). Эти два значения, в свою очередь, связывают третий важный элемент в расчете двигателей—коэфф-т подачи:

^⁼ 7 78о· !,;^ca^(1+L)’ ⁽⁶⁵⁾

где С_с расход топлива на эффективный силочас в килограммах. В тех случаях когда проектируется новая машина, для которой возможна оценка частных коэффициентов рабочего цикла по аналогии с отдельными деталями уже существующих двигателей, желательно произвести полный тепловой расчет, выявляющий точную термодинамич. связь основных величин, входящих в расчетное уравнение (65).

Действительное количество воздуха, введенного в рабочий процесс, будет: для газообразного топлива: L=L₀a ке-мол., для жидкого топлива: L"= _2Ч=L₀a ita-мол. (где 28,95—вес 1 килограмм-мол. воздуха, I—количество воздуха в килограммах на 1 килограмм жидкого топлива). Остаточный коэфф-т у будет: для четырехтактных двигателей

У , ¹. ^р’·. ^Т»;

^Г »7» (ε — 1) Ре Т г для двухтактных двигателей

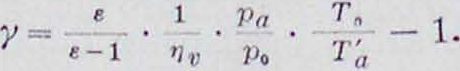
Число кг-мол. в цилиндре перед началом сгорания будет равно: для газообразного топлива (14 L)(l+y) кг-мол., для жидкого топлива ¹ - (14-у) кг-мол. Во время сгорания число кг-мол. введенной смеси изменится на AM. и коэффициент молекулярного изменения β определится для газообразного топлива из выражения

^⁼¹+ЦТ№->.) («6)

и для жидкого топлива—из выражения т — · (07)

28,95 ^ ⁺⁷⁾

Отношение числа кг-мол. остаточных газов к числу кг-мол. продуктов сгорания (без остаточных газов) будет равно: для газооб разного топлива

(1+L)y 1+L+&M ’

(68)

для жидкого топлива I

у

28.95

—— + дм

28,95

(69)

Пользуясь выражениями (66), (67), получаем:

(1 + L)y__ у

Г L) (1+У)-(Х+Ь)У ” fi ~ /(i-fi) ⁹ l

- у

28.95 _

i i _ А

28.95 ^Υ 28,95

У

/S-y(l-/3)

В виду незначительности у и близости β к 1 последний член в знаменателе м. б. откинут, и все отношение остаточных газов к сгоревшим, выраженным в килограммах-мол, моя·: и о приравнять ^у.

Из всего введенного в рабочий цикл количества тепла Я" 24,4II, на 1 килограмм-мол. газообразного топлива или h„ на 1 килограмм жидкого топлива за фазу видимого сгорания соответственно используется ξΗ" или >/?,, где £— коэффициент выделения тепла. К этой термохимич. энергии должен быть прибавлена термодинамическая энергия в конце сжатия рабочей смеси (А + В Т_с) Т_с—и остаточных газов, составляющих долю ^у от сгоревших газов: ^ν (А" + В”Т^Т_С. Выражения: А"+

f В" Т — суммарная средняя теплоемкость продуктов сгорания, полученных при сгорании ί кг.-мол. газообразного топлива или 1 килограмм жидкого топлива, А + ВТ—та же величина для рабочей смеси. После сгорания теплоемкости остаточных газов и сгоревших газов одинаковы, и необходимо суммарную теплоемкость сгоревших газов отнести ко всей сумме сгоревших газов плюс остаточные, то есть увеличить А” 4- ВТ_г в |l 4-раз. Тогда ур-ие сгорания примет вид: ξΙ1ΐ + (Λ + BT_e)T_c+ ^γ (А” + В"Т_С)Т^

- (l + 3 (Λ" + В" Ί )Τ_Ζ. (70)

В этом ур-ии теплоемкости берутся согласно рабочему процессу: для цикла Отто—теплоемкости при постоянном объёме, для цикла Дизеля—при постоянном давлении. 11з ур-ия (70), зная темп-ру в конце сжатия Т_с, опре деляемую из ур-ия политропы: 7’„=Т_анаходим темп-ру сгорания Ί. Для определения давления вспышки ρ_ζ для цикла Отто имеем следующее соотношение: ρ_ζ=βρ,..

где β—коэффициент молекулярного изменения, то есть β= *·, и р_е р„е^п>. Для определе-ния степени предварительного расширения ρ для цикла Дизеля имеем: ρ=β .j^?, где

/?=;j^!(l4- J), причем Н_г относится к чи стому воздуху плюс остаточные газы, а R₂ к продуктам сгорания. Поправка (l 4- ’)

обусловливается изменением количества рабочего тела после сгорания на величину введенного 1 килограмм топлива. Значения р_е и Т_е в конце политропнческого расширения определяются из выражения: р_с=^ и Т_с - -,

где <5—степень расширения (для цикла Отто δ=ε, для цикла Дизеля δ —

На основании полученных давлений и изменений объёмов определяются средние теоретические индикаторные давления: для двигателей быстрого сгорания

Р_С In,^{1 1} ««,-Д.

‘ β-l (j η,-l I’

(71)

для двигателей Дизеля: Pi

1CU .и И

¹ e -1 ~ п_г-1

1

Пх- 1

/·

(72)

Действительные средние индикаторные давления получаются из теоретических путем помпожепия на поправочный коэфф-т μ (полноту диаграммы) и за вычетом отрицательной работы на всасывание и выталкивание газов Ар, то есть р=pp_t — Ар. На основании полученного среднего индикаторного давления можно определить по вышеприведенным формулам индикаторный кпд щ и расход топлива на индикаторную силу в час С^ а задаваясь механическим коэффициентом полезного действия η„,—те же значения, отнесенные к работе на валу машины.

Регулирование. Задачей регулирования является поддержание соответствия между мощностью, снимаемой с машины, и количеством тепла топлива, преобразуемым в меха-ническ. энергию. В стационарных установках обычно двигатель работает при постоянном числе оборотов, причем органы регулирования находятся под воздействием авто-матич. регулятора. Регулирование Д. в с., работающих на газовом или карбюрированном жидком топливе, бывает качественное, количественное и смешанное. Качественное. регулирование состоит в изменении состава рабочей смеси; количествен-н о е—в изменении степени наполнения смесью цилиндра при сохранении одного и того же ее состава, и, наконец, регулирование смешанное представляет собой комбинирование того и другого. К количественному регулированию молено отнести и регулирование «пропусками», состоящее в полном прекращении подачи топлива при возрастании числа оборотов двигателя. Этот способ регулирования является стермическ. стороны наиболее выгодным, т. к. неизменяемость состава смеси, выбранного заранее, обеспечивает полноту горения и рабочая смесь после пропусков не загрязнена остаточными газами. Однако, отсутствие вспышек во время пропусков ведет к большой неравномерности хода двигателя, что влечет за собой необходимость больших маховиков. Поэтому регулирование пропусками применяется в двигателях малой мощности.

Количественное регулирова-н и е. Количественное регулирование достигается двумя способами. Первый способ

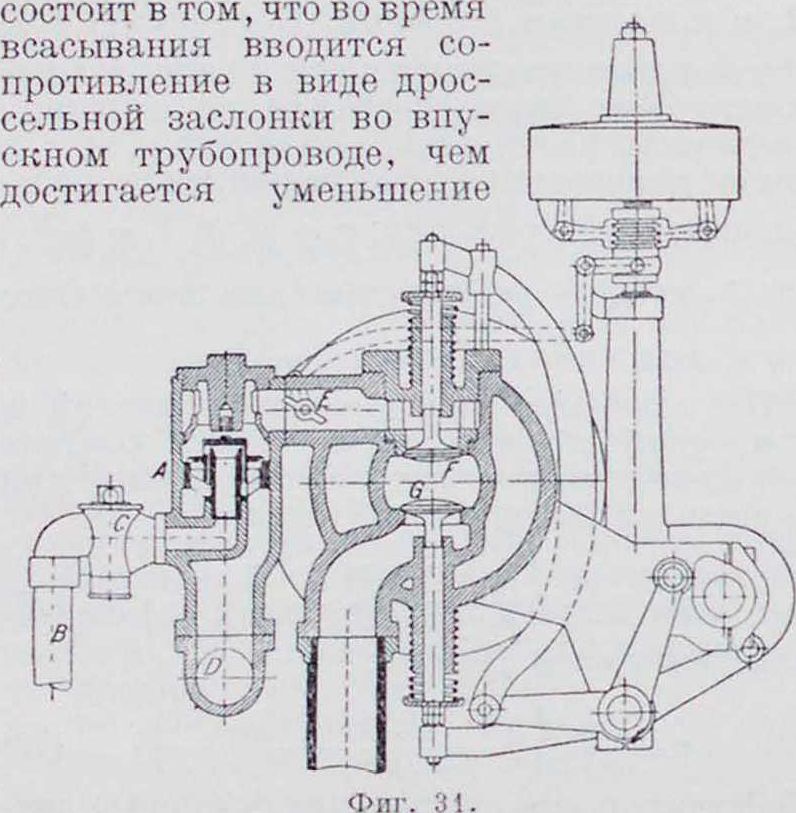
количества всосанной смеси; при втором способе сопротивление отсутствует, уменьшение же количества смеси достигается тем, что в определенный момент всасывающего хода газовый и воздушный клапаны закрываются. Недостаток количественного регулирования заключается в том, что при малых нагрузках получается слишком малое давление сжатия и инерционные усилия становятся больше давления сжатия, в результате чего кривошипный механизм под влиянием сил инерции будет прижат в конце сжатия к частям вкладышей поршневого болта, шатунной головки и коренного подшипника. В момент вспышки, при быстром увеличении давления в цилиндре, рабочее давление будет передаваться на противолежащие стороны вкладышей, и, в виду существования трех зазоров, эта перемена давления произойдет при большей скорости поршня, что вызовет стуки в кривошипном механизме. Избежать этих стуков при малых нагрузках можно применением более бедных смесей, для чего потребуется при той же нагрузке большее наполнение цилиндра, вследствие чего давление в конце сжатия повысится до величины большей, чем сила инерции, то есть частичным переходом к качественному регулированию.

Качественное и смешанное pfr г у л и р о в а и и е. Качественное регулирование, по сравнению с количественным, обладает тем достоинством, что сжатие при нем остается неизменным. Недостатком же ого является то, что при малых нагрузках, то есть при пользовании бедными смесями, можно выйти из пределов воспламеняемости данного топлива и не получить вспышки. Кроме того, при качественном регулировании, для получения правильной диаграммы приходится для разных нагрузок переставлять запал. Желание избегнуть недостатков качественного н количественного регулирования и воспользоваться их достоинствами привело к смешанному регулированию, при к-ром, в зависимости от величины нагрузки, пользуются то количественным то качественным регулированием. Смешанное регулирование выполняется различно. Рейн-гарт, например, в своем регулировании впускает сначала воздух, а затем газовую смесь постоянного состава. Рабочая смесь предварительно пропускается через смешиватель-ный прибор, что обеспечивает хорошую диффузию смеси, подлежащей сжиганию, оставляя заранее всосанный воздух инертным. Во многих других способах смешанного регулирования при больших нагрузках прибегают к регулированию качества смеси, при переходе же к малым нагрузкам—регулированию ее количества.

К о н с т р у к т и внос в ы и о л н е и и е регулирования. Количественное регулирование бр. Кертииг является одной из типичных конструкций. Как видно из фигура 31, газ поступает по трубе В через вентиль С в смешивательную камеру А, куда также входит по трубе D воздух в направлении, перпендикулярном движению газа; этим достигается хорошее перемешивание. Из смешивательной камеры А рабочая смесь поступает в цилиндр двигателя по каналу Е, в котором помещается дроссельная заслонка, управляемая регулятором. Клапан G служит для выпуска газов, а клапан F—для впуска; оба клапана работают от распределительного вала с помощью кулачковых шайб. При увеличении числа оборотов дроссельная заслонка в канале Е, уменьшая свободный проход рабочей смеси, изменяет ее количество, поступающее в цилиндр; качество же смеси остается все время неизменным, благодаря двухопорному клапану, открывающему при разных подъемах пропорци-ональн. сечения для протока газа и воздуха, и м.б. изменяемо лишь вручную, путем изменения открытия газового крана. В конструкции завода Дейц (фигура 32) Фигура 32. регулирование про исходит след, образ.: кулак d действует на ролик /, укрепленный на длинной штанге, и через криволинейный рычаг д передает движение двухопориому клапану ab, управляющему впуском газа и воздуха. При изменении числа оборотов двигателя регулятор, посредством сист. рычагов, поворачивает вокруг точки О коленчатый рычаг h с сидящим на нем роликом, меняющим соответственно этому точку опоры рычага д, чем и достигается изменение со-

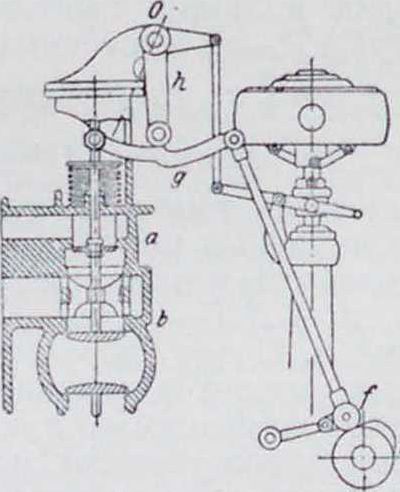
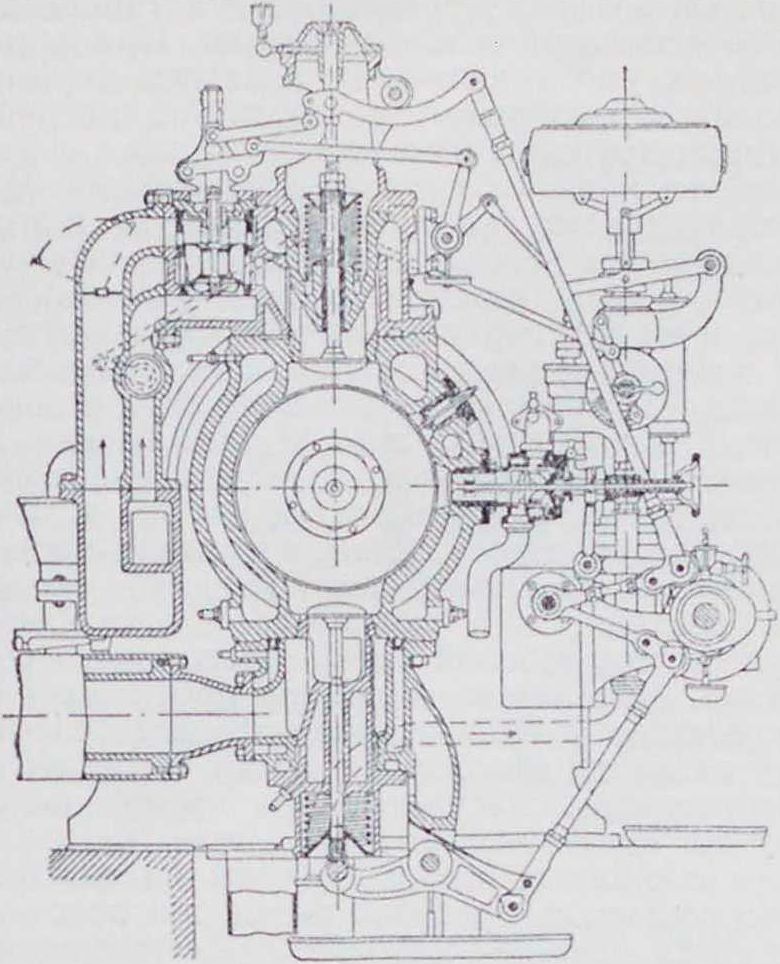
отношения его плеч и в зависимости от последнего большее или меньшее открытие клапана. Эта конструкция па практике оказалась очень удачной и в несколько измененном виде применяется и для двигателей

Ч<Ш·. 33.

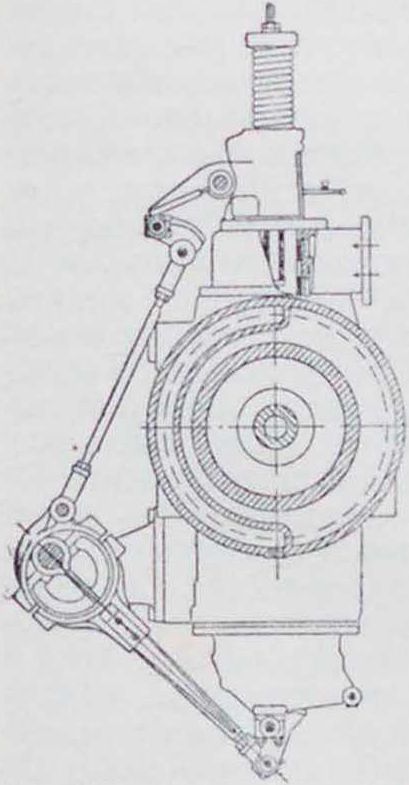
больших мощностей.В этом случае (фигура33) смешивательный прибор, во избежание перегрева и для более удобного ухода, монтирован отдельно. Регулятор действует только на смешивательный прибор; подъемы же всасывающего и выхлопного клапанов остаются постоянными. Газ и воздух все время, кроме периода всасывания, разобщены. Впуск воздуха начинается несколько ранее открытия газового клапана; воздух таким образом обгоняет газ и, как бы окружая его, устраняет возможность преждевременного воспламенения. Для остановки двигателя имеется особое приспособление у регулятора, закрывающее газовый капал. Недостатком этой конструкции, как и вообще количественного регулирования, является необходимость ставить очень сильные пружины на Фигура 34. всасывающем и вы хлопном клапанах, так как при малых нагрузках, то есть при малом количестве рабочей смеси, в цилиндре образуется разрежение,доходящее иногда до 0,5 aim, и выхлопной клапан может открыт!,си под влиянием разрежения; сильные пружины, в свою очередь, вызывают силь ные удары клапана о седло и быстрое его изнашивание. В позднейшей конструкции завод Дейп устранил эти недостатки: он сделал принужденными все движения открытия впускного и выхлопного клапанов, достигнув этой управляемости при помощи системы ломаных рычагов.

Количественное регулирование завода Вести и ray з изображено па фигура 34. Смешивательпый орган, в виде круглого золотника с окнами для воздуха и газа, сидит на шпинделе всасывающего клапана. Регулирование достигается поворачиванием круглого золотника, чем изменяется сечение прохода для газа и воздуха. Регулятор действует на золотник через сервомотор. Применение смешивательных золотников, связанных с всасывающим клапаном, возможно исключительно при очень хорошо очищенном газе и при принужденном движении клапана, так как не исключена возможность заедания золотника.

На фигуре 35 дан разрез через клапанную головку с видом на распределение и регулирование газовсасывающего горизонтального двигателя Швейцарского паровозостроительного завода в Винтертуре. Всасывающий и выхлопной клапаны приводятся в движение от кулачков распределительного вала помощью рычагов и толкающих штанг. Отсечный золотник, в виде двухопорного клапана, посаженный на трубчатой штанге, получает свой подъем через двуплечий рычага, штангу Ь и угловой рычаг с от кулачка d, посаженного на обойме эксцентрика е, сидящего па распределительном валу; точка

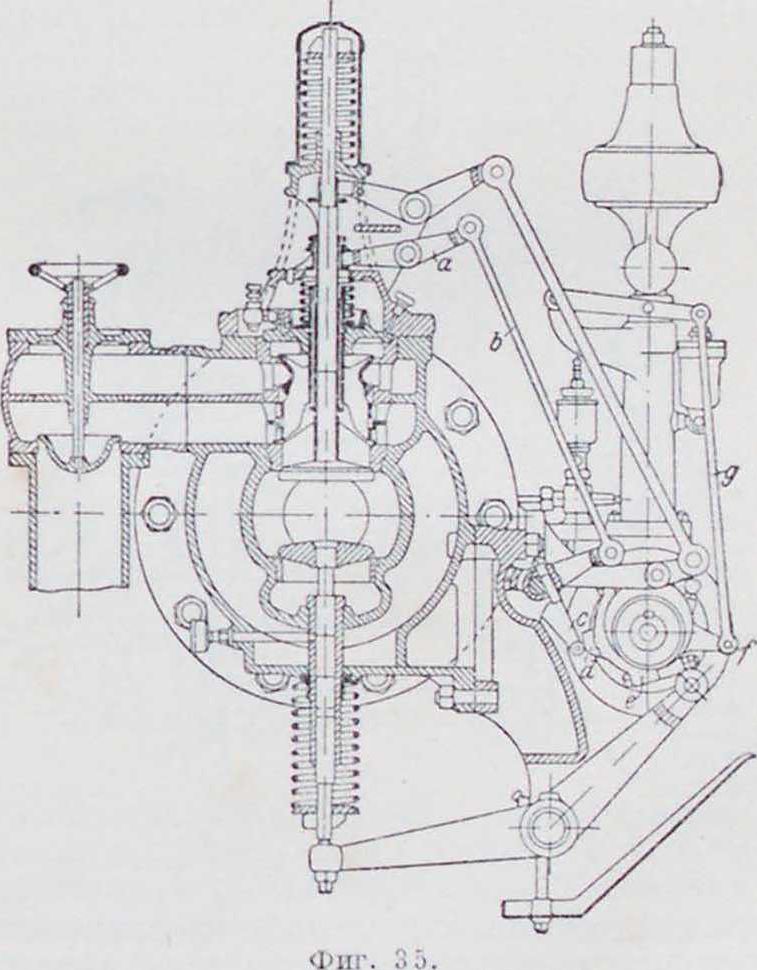
обоймы через штангу д связана с муфтой регулятора и тем изменяет момент соскакивания ролика с кулачка d и закрытия отсечн. золотника. С момента закрытия последнего происходит расширение засосан, смеси без дросселировании ее, и линиц сжатия совпадает с линией предшествовав]!!, расширения.

Качественное регулирование. Наиболее простой и удачной конструкцией качественного регулирования является конструкция Нюрнбергского з-да, применяемая для крупных двигателей (фигура 36). Здесь дросселируется только один газ; впуск же воздуха остается постоянным. Самый процесс регулирования происходит следующ. образом: эксцентриковая штанга b помощью ножа b перемещает рычаг а, который подымает или опускает газов, клапан. Рычаг а катится по подушке рычага d, перемещаемого от регулятора посредством ломаного ры-Фигура 36. чага е. Перемещение рычага d меняет точ-кудэпоры рычага а, в зависимости от чего изменяется момент начала подъема клапана. С рычагом а связан воздушный тормоз /, способствующий более плавной посадке клапана на седло. К этому буферу прикреплен ролик с который размыкает нож от рычага а в момент окончания процесса всасывания.

Смешанное регулирование. На фигуре 37 дана конструкция смешанного регулирования Рейнгарта. Круглый золотник, перекрывающий три ряда окон, управляет впуском газа и воздуха в емешивательный прибор; верхние окна с и нижние а служат для впуска воздуха, средние b—для газа;

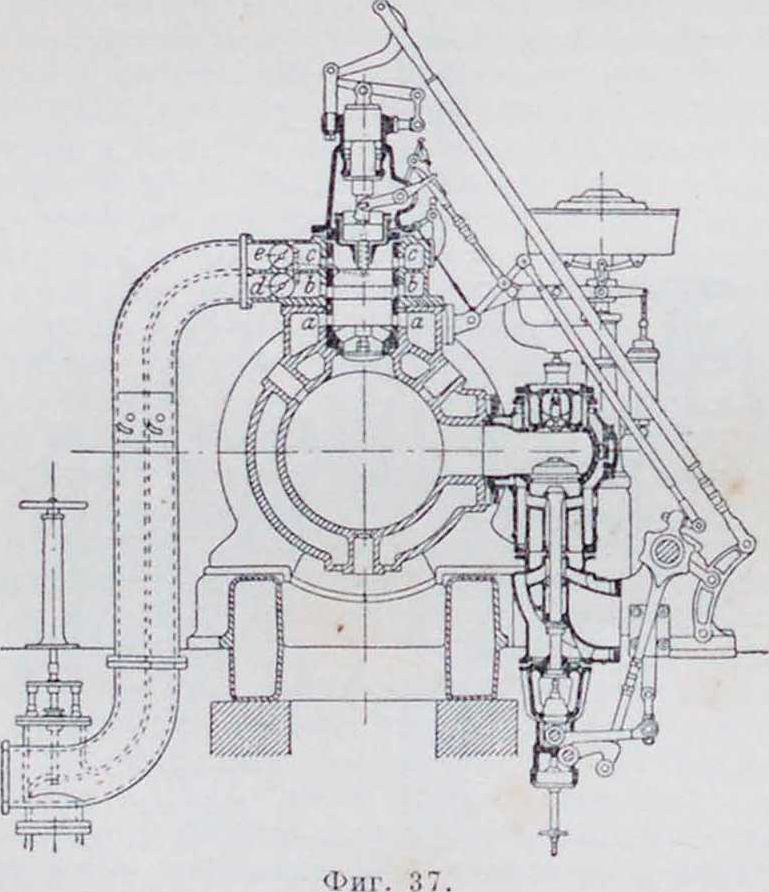
нижний ряд окон служит для предварительного впуска воздуха. Кроме того, имеются еще две дроссельные заслонки е и d в воздушном и газовом трубопроводах. Перед началом всасывающего хода круглый золотник находится в нижнем положении, и открыт!, i только верхние два ряда окон, но газ и воздух в них не поступают, т. к. дроссельные заслонки перекрывают впуск. Когда всасывающий клапан действием эксцентри ковой штанги открывается, то золотник, связанный с другой штангой от того лее эксцентрика, начинает подниматься и, закрывая средний и верхний ряд окоп, открывает нижние окна, через которые входит чистый воздух, устремляющийся в цилиндр и оттесняющий остаточные газы. При дальнейшем своем движении золотник особым роликом разобщается со штангой и под действием пружины идет вниз, открывая верхние два ряда окон и закрывая нижний ряд для предварительного впуска воздуха. К этому.времени дроссельные заслонки, связанные с всасывающим клапаном, уже открыты, и через верхние окна поступают газ и воздух, перемешиваются и входят в цилиндр. В конце хода всасывания всасывающий клапан закрывается, так лее как и дроссельные заслонки, золотник снова сообщается со штангой, и все готово к следующему процессу. Итак, в цилиндр поступает сначала переменное количество чистого воздуха, а в конце—соответствующее количество газовой смеси постоянного состава. Наполнение цилиндра продолжается в течение всего всасывающего хода, почему давление сжатия все время и остается постоянным. Регулирование производится путем изменения момента открытия окоп для составных частей рабочей смеси. Конец всасывания рабочей смеси при всех нагрузках бывает постоянен. Достоинством регулирования Рейнгарта является то, что предварительно впущенный воздух, отгоняя остаточные газы, сам мало перемешивается с впущенной вслед за ним в цилиндр рабочей смесью, благодаря чему к моменту сгорания мы всегда имеем чистую однородную смесь наивыгоднейшего состава. При переменных нагрузках зона, разделяющая чистый воздух и рабочую смесь, меняет свое положение, и при полной нагрузке в цилиндр поступает только рабочая смесь. В этой конструкции выхлопной клапан монтирован сбоку, что облегчает возможность хорошего охлаждения и уменьшает размер конструкции, по, с другой стороны, является недостатком в термич. отношении, т. к. пространство сгорания является вытянутым в виде трубы, что ухудшает сгорание.

На несколько ином принципе основана конструкция смешанного регулирования Месса (фигура 38 и 39). При переходе от больших нагрузок к малым качественное регулирование становится невыгодным, так как с переходом к более бедным смесям воспламенение, а с ним и теплоиснользование ухудшаются. Поэтому является более выгодным, в целях сохранения хорошего теплоисполь-зовання, при малых нагрузках переходить к количественному регулированию. Это и делает Месс в своей конструкции, сохраняя при этом определенный, наивыгодней-шнй для данного топлива состав смеси. С<> шпинделем всасывающего клапана связан при помощи пальца у поршневой золотник к с двумя рядами окон г_х и ш_г, которые открывают соответственно воздушный канал г и газовый канал т. Шпиндель клапана движется в трубке р_1г связанной вверху при помощи шарнира I с регулятором и получающей от пего вращательное дви-

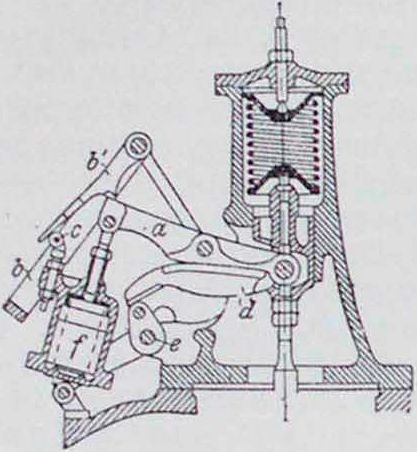
жоние, которое она передаст, захватывая внизу палец с/, поршневому золотнику к. Окна поршневого золотника расположены таким образом, что газовый канал начинает перекрываться, а окна для впуска воздуха остаются еще некоторое время открытыми полностью. Лишь при малых нагрузках

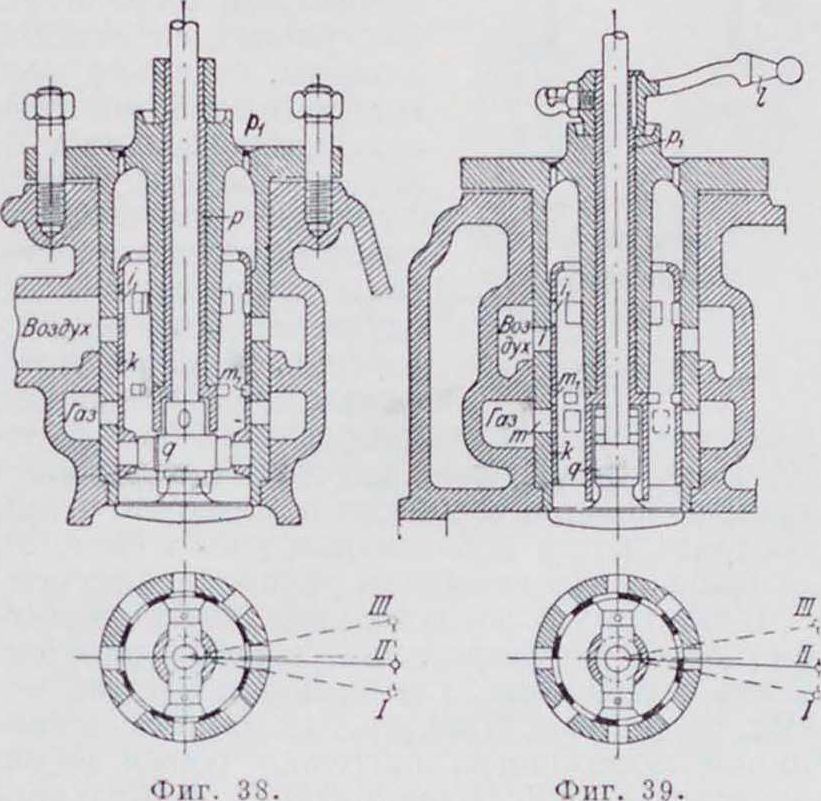
(положение III на фнг. 38 и 39) вместе с газовыми окнами начинают перекрываться и окна для воздуха, то есть дросселируются одновременно и газ и воздух, и регулирование из качественного становится количественным при наилучшем качестве смеси, установленном заранее. Положение I на фигуре 38 и 39 соответствует положению при перегрузке двигателя, когда газовые окна открыты наиболее полно и в цилиндр поступает богатая смесь. Положение II соответствует норм, нагрузке. Регулирование Месса дало на практике хорошие результаты.

Конструктивное описание Д. в с. см. Двигатели газовые, Двигатели Дизеля, Двигатели судовые, Двигатели нефтяные мелкие.

Литсм. Двигатели Дизеля. Н. Брилинг.