Движение воды

Движение воды. Законы Д. в имеют широкое применение в гидротехнике при расчетах каналов, трубопроводов, плотин, вы-правительных и других сооружений. Д. в бывает равномерное и неравномерное, без напора и с напором.

Движение воды в открытых руслах, а) Равномерное д в и ж е н и е вод ы. Необходимым условием равномерного Д. в является постоянство живого сечения, материала и характера(шсроховатости) русла, уклона дна и расхода воды. При этих условиях из основного уравнения для установившегося движения жидкости (смотрите Гидравлика) получает ся следуют, формула III о з и (Ch6zy)для равномерного Д. в открытых руслах: v=kVRi, где V—средняя скорость водотока, к—опытный коэффициент,

пять равным 50, вообще же для определения к был предложен целый ряд формул.

Наиболее употребительными были до последнего времени (примерно до 1925 г.) и применяются в нек-рых странах до сих пор: 1) Ф - л ы Г а н г и л ье-Кутте р а: (Ganguillet- Kutter):

„О, ¹, 0.00155

Λ 0,00155	1 ¹¹
1 + 23 +
* )	¹ i Ш

Для уклонов г0,0005 можно пренебречь членом тогда к=^23 + ^) : (i + 23 ^ ^ j

или применить так называемую старую формулу Куттера: к=¹⁰⁰ ^ “

т+У R

2) Ф-л а Б а з e η a (Bazin):

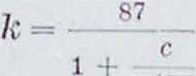
I R

В ф-лах Гангилье-Куттера и Вазона и, т и с называются коэфф-тами шероховатости; значения их для наиболее характерных состояний русла смотрите ниже в таблице 1.

С 1925 г. (преимущественно в Германии) формулы (1) и (2) вышли из употреблении, и при расчете открытых русел стали применяться более простые степенные формулы, а именно:

3) Ф-л a Man н и и г a (Manning):

4) Ф-л а Форхгеймера (Forchheimer): V _ ¹ д».’. i»’^s.

В формулах (3) и (4) коэффициент шероховатости п тот же, что и в формуле Гангилье-Куттера (смотрите табл. 1).

Таблица 1. — Значения к о о ф ф и и и е и т о в п, т и с д л п различных русел.

№	Русла	п	m	с
I	Русла с очень гладкой обделкой (цементной, из гладко выстроганных досок).	0,010—0.014	0,12—0.15	0,06
II	Русла с гладкой обделкой (из тесовой или кирпичной кладки или пеостроганных досок) ..	0,016—0,018	0.20—0,25	0.16
III	Русла с грубой обделкой (из бутовой кладки, булыжной мостовой) ..	0,020—0.023	0,35—1,00	0,46
IV	Русла земляные правильной формы..	0.025—0.02S	1,50—1,SO	0,85
V	Русла земляные в обычных условиях с небольшим количеством гравии и водорослей ..		1,50—2,00	1,30
VI	Русла земляные с крупными камнями или обильно за-росшие..	0,040	2,00—2,20	1,75

R=у—гидравлический радиус, равный отношению площади живого сечения к подводному (смоченному) периметру U, и г— уклон потока. Величина к -изменяется, в зависимости от шероховатости русла и его конфигурации, довольно значительно. При приближенных вычислениях его можно прн-

Приведеиные ф-лы находят применение гл. обр. при расчете искусствен, каналов; при расчетах же естественных потоков (особенно рек с подвижным ложем) пользуются ф-лами, где отсутствуют и коэфф. шероховатости и R. Таковыми являются ф-лы Кристена (Christen), Матакевича (Matakiewicz), Линдбое (Lindboe), Германека (Ilermanek).

5) Ф-л а Кристе н а:

V=т П_т· г /В,

где В—средняя ширина, —средний глубина русла, т—коэффициент, характеризующим степень насыщенности рек наносами; для рек с наносами т=7, а для рек без наносов m=32; для каналов же, если придерживаться приведенных выше в формулах Базена и Гангилье-Куттера подразделений обделки русел, значения для m: I—57—54,

II—56 52, III—39—30, IV—28—20, V— 18—10 и VI—11.

0) Ф-л а Матакевича: по i⁰^498+loi

2,2+(_ш ¹т

Имеется таблица, приведенная у Вейрауха, дающая непосредственно среднюю скорость V при от 0,1 до 7,0 метров и уклонах г от 0,000025 до 0,01. Средние скорости колеблются от 0,028 до 8,993 м/ск.

7) Ф-л а Л и к д б о е действительна для естественных потоков при B_min=10 .и, г_тпх=

=0,005, (⁽”Л =0,1 и выражаетv=k-λC.-i’’.

Для различных значений г, ί,„ и численные значения коэффициентов сведены в следующую таблицу, дающую значения ν.

8) Для рек с подвижным ложем Германек дает следующие простые степенные формулы:

ПРИ 1_т <1,5.4 V=30,7 !,„ Д

* 1,5ί Ι,ιΐβ.«.υ=34,0 1,Д ii

* 1т > 6 ·«..t> — 44,5 t°· i°‘‘

Прежде чем остановиться в расчетах гидротехнических сооружений на определенной формуле, необходимо тщательно проверить имеющиеся результаты непосредственных измерений с данными, полученными по возможности в том лее районе но различным ф-лам, и остановиться на той из них, при к-рон суммы положительных и отрицательных отклонений вычисленных величин от измеренных наиболее близки друг к другу и при которой получается наименьшее число крупных отклонений (например, больше 0,2 лисит¹). Вообще лее для предохранения русла искусствен, потоков от размыва нельзя допускать ν выше след, пределов для различных грунтов (в λι-схг¹): илистая земля и мягкая глина—0,10; жирная глина—0,15; глина и крупный речной песок—0,30; хрящ—0,61; гравий—0,91; грубокаменистый грунт—1,22; сланец и конгломераты—1,83; тяжелая галька—2,25; скала—3,05. Для мостовой средняя скорость принимается от2,0 до 2,5 м/ск, для каменной кладки и деревянных лотков—до 4,0 м/ск. Для предохранения от осаждения наносов средняя скорость не должна быть меньше 0,25 м/ск при илистых и 0,50 м/ск при песчаных наносах.

Выбор формы и размеров каналов зависит от целого ряда условий. Расход Q обычно задан заранее, площадь живого сечения F определяет объём выемки, а следовательно, и стоимость канала; подводный периметр U определяет стоимость обделки и укрепления дна и откосов; при отсутствии укрепления форма каналов определяется углом естественного откоса грунта. Пределы колебания скорости зависят от условий размыва и отложения наносов; увеличение уклонов часто сопряжено с опасностью понижения полезного напора воды. При учете всех указанных условий наивыгоднейшие размеры каналов определяют методом последовательных подстановок и приближений, задаваясь различными скоростями и подбирая ту наивыгоднейшую скорость, которая и соответствует наименьшим затратам как строительным, так и эксплуат-оиным. Различные формы поперечных сечений каналов и их расчеты— см. Каналы. б) Неравномерное д в и ж ение βοή ы характеризуется изменением средней скорости ν при переходе от одного сечения к другому и вызывается всяким изменением живого сечения или уклона потока. Плавное повышение водной поверхности в зависимости от преград или сужений русла (плотина, мостовые быки) называется подпором, плавное же понижение поверхности—спадом, резкий подъем — прыжком воды, резкое понижение—водопадом. При математич. решении вопросов неравномерного Д. в исходят из предположения медленных изменений живых сечений, а следовательно, и средних скоростей. Поэтому формулы неравномерного движения относятся по преимуществу к искусственным каналам, а не к естественным руслам. Основное уравнение неравномерного движения воды имеет вид:

dz _ d /сП ιφ dx~ dx 2g)⁺kR ’

Таблица 2. — Значения ν в м-гк

Средняя глубина русла	Уклон: i < 0,0006
	-jj? < 0,028		0,028 <’” < 0,1
< 1,12 .*4 1,12 .«< !_т<3,65.м t т > 3,65 м	23,37^0,822-24,11^0,822 - ~ 27,45^0,822 -	1 ·· i·,. т у.» т [ ·»** _t*0,4J т	,, 8,19 ί 2,293- "jl^* i·" 8,45 ^ 9,62 f 2,293 V В) m
Средняя глубина русла	Уклон: 0.0006 < i < 0.005
	⁽,^т <0.028		0,028 < ~ < 0,1
1_т < 1,12 .« 1,12 .«< <3,65 .« 1т > 3,65 м	33,36^0,822 -34,94 (о,822 -39,77 ^0,822	1°⁹ (0,п т jO»·* ^0,17 т Ii⁰” т	11,80(2,293 - V B ^m 12,24^2,293 -13,94^2,293 -

где к—коэфф. формулы Шези. Если известна зависимость R и F от х, то уравнение неравномерного движения можно интегрировать, т. к. при известном F условие постоянства расхода дает зависимость г от х и V. После интегрирования получаем зависимость ζ от х, т.е. кривую свободной поверхности. Интегральное ур-ие вида

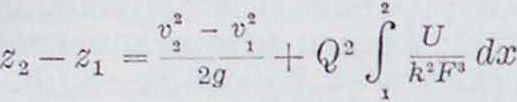
может быть решено последовательными приближениями, если на конечном участке 1—2 известны продольный профиль русла и ряд живых сечений. Целый ряд упрощающих допущений, в частности о призматич. форме русла канала при большой его ширине

Фигура 1. Фигура 2.

по сравнению с глубиной, позволил исключить из уравнения площадь живого сечения и заменить величину R глубиной русла t. Удельная энергия « потока при атмосферном давлении (открытом русле) и глубине I

равна: «=+ t. Ту глубину потока t_k, кото-

рая соответствует минимуму удельной энергии, называют критической. Из уравнений

, ⁰ и ^г’= t_kH находим: t_k j _w,-

Глубину t_B, которая установилась бы в потоке," если бы при данном уклоне дна г движение перешло в равномерное со скоростью v, называют нормальной. Из ур-ия Шези

V=к_а у R₀i и Q =13t_Bv находим: t_B=j ·

Ур-ие неравномерного Д. в функции глубин имеет вид:

di _. t’ -tl ^{dx 1} i’- tit

По критической глубине все потоки делят на две категории: при t > t_k они обладают

Фигура 3. Фигура 4.

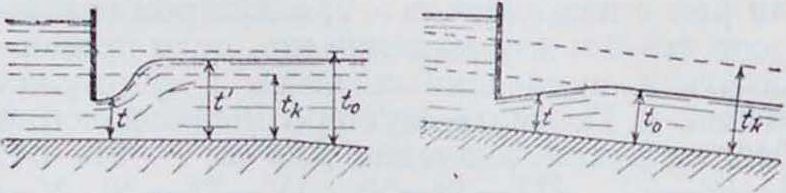
спокойным течением, при t < t_k—бур-н м м. В зависимости от отношений между i, t„ и t_k различают следующие виды неравномерного Д. в.

1) <о=t“; ][[.=i. Свободная поверхность горизонтальна, и глубина t возрастает вниз по течению (фигура 1 и 2).

2) t > 1_В > t_k ”>0. Свобода, поверхность вниз по течению приближается к горизонт, прямой приближается к г), а вверх по течению — к прямой равномерного движения приближается к нулю! (фигура 3).

3) t_B>t>t_k; <0. Кривая спада (фигура 4).

4) t₀> t_k> f; _dv>0. Прыжок воды. Глубина постепенно возрастает вниз но течению, приближаясь к величине 1_к. В момент

Фигура 5.

Фигура G.

достижения этой величины свободная поверхность поднимается вверх и переходит внезапно к режиму V > i_k (фигура 5).

5) t<t_B<t_k; > 0. Свободная поверхность приближается к прямой равномерного движения воды (фигура 6).

G) t_B<t< t_k; ^ < 0. Кривая спада приближается к прямой равномерного движения воды (фигура 7).

7) <„ < t_k < > 0. Кривая подпора, начи нающаяся с прыжка воды и приближающаяся к горизонтальной линии (фигура 8).

Построение и расчеты отдельных кривых свободной поверхности при неравномерном движения воды см. Подпор.

Движение воды в трубах. Потеря напора Н на длине L трубы, или гидравлич. уклон данной трубы, рассчитывается по ф-лам вида г=ζ где D—диаметр трубы (в л«),

или г — λ ^, причем последняя формула может быть при приближенных вычислени ях заменена такой:

Из большого числа эмпирических формул (свыше 150) Д. в трубах приведем наиболее употребительные.

1) Ф-л а В е и с б а х a (W eisbac h):

ζ - 0,01439 + ⁰’⁰⁰⁹·¹⁷¹¹.

1 w

2) Ф-л а Д а p с и (Dare у):

ξ- 0,02 +

0,00051

3) Ф-л а 3 о н и е (So η η о):

1 /,.. 0,012 I U 0,003. 1

1θ6ν^υ,υ° D J D

4) Ф-л а Лампе (L a m р е):

г а

D^lM

где в среднем а—0,0007555.

Для большинства формул во всех справочниках приведены таблицы или графики, позволяющие по двум из величин Q, r, J) и г определять остальные.

Кроме общей потери напора, в трубах от трения существуют еще потери от местных сопротивлений (смотрите Гидравлика), выражав-мые ф-лой;^Ιί! ζ.,, · ^- Значения ζ для различных случаев местных сопротивлений (при входе, в коленах и отводах, при уширении и сужении, в запорных приборах) приводятся в справочниках (lliitte и др.).

Лит.: П а в л о в с к и и 11. Н., Гидравлический справочник. Л., 1924; Вахметев В. А., О неравномерном движении жидкости в открытом русле, Л., 1928; Эссен А., Формулы скоростей. Отчет гидравлической части на е за 1910—12 гг., Тифлис, 1913; W e i г а и с h It., Hydraulisches Rechnen, Stg., 1926; S i e d e k It., Studle liber cine neue Formel zur Ermittelung d. Gescliwindigkeit d. Wassers in Fliissen u. StrOmen, Wien, 1901; Christen T., Das Gesetz d. Translation d. Wassers in regelmassigen KanaleH, Fliissen u. ItOhren, Kpz., 1903. А. Эссен.

Движение грунтовых вод. Грунтовой воде, при движении в водопроницаемых слоях грунта, приходится преодолевать большое сопротивление вследствие трения частиц воды между собой и о стенки пор грунта. Эти сопротивления в зависимости от свойств грунта могут достигнуть больших величии и заставляют воду двигаться весьма медленно. Скорость воды обыкновенно менее 1 j» и редко более 5 метров в сутки. Влияние свойств грунта сказывается и на характере движения водяных струек, которое подчиняется законам вязкистп и фильтрации.

Вязкость. При медленном движении и малом поперечном сечении, движение воды но взаимно скользящим слоям но сопровождается каким-либо внезапным изменением скорости между двумя соседними точками. При этом движении разность dv скоростей в двух соседних слоях, находящихся на расстоянии dn друг от друга, вызывает трение которое стремится движение одних частиц : ускорить, а Других- замедлить. Всть характеризуется внутренним коэффициентом трения г — Const, измеряемым силой, помноженной па время и деленной на площадь. По Пуазейлю (Poiseuille), при температуре воды Т°

0,00001814 _ __ ____.,

™ ⁼ 1 + 0,033? Т +0.00022 T ^{3 СК} ^С^Н ’ ~ 0,0001814 ₂

1 +0,0337 Т+ 0,00022 Г· ^{1,3 СК}

Фильтрация. Дарси (Darcy) в своих опытах с песчаными фильтрами нашел следующую зависимость:

Q - к · · F. (2)

В этой формуле Q—количество воды в м³, протекающее через фильтрующий слой в 1 секунду, h—разность между уровнями воды перед фильтром и после фильтра в .и, I—кратчайший путь, который вода должна пройти сквозь фильтр, или толщина фильтрующего слоя в см, F- площадь поперечного сечения фильтрующего слоя в м³, к—коэффициент пропускной способности грунта и е.н-ск^-1, равный для чистого песка (В6 ; -50) d-, где d— средний диаметр зерен песка.

Формулу (2) можно преобразовать следующим образом:

где р—пропускная способность грунта, то есть количество воды, протекающее в единицу времени, при скорости равной единице, через фильтрующий слой, площадь которого равна единице, a v— средняя действительная скорость протекающей через фильтрующий слой воды. Ф-лы (2) и (3) говорят, что потеря напора h пропорциональна скорости или количеству воды, протекающему сквозь фильтрующий слой. Этот закон имеет, однако, место лишь для мелкого песка и для скоростей, обычных при медленной фильтрации. Поэтому закон Дарси не может быть применен для всех случаев движения грунтовых вод, т. к. в крупнопесчаных и гравелистых грунтах и при больших скоростях движения воды, чем в условиях медленной фильтрации, потери напора пропорциональны уже не первой степени скорости или количеству воды, а высшим степеням скорости.

3 а к о н с о и р и т и в л е н и я движению грунтовых вод. Смрекер (Smreker), исследуя движение грунтовых вод, указал на то, что коэффициент к пропускной способности грунта ость ф-ия скорости v.

Если грунтовая вода движется в водоносных пластах с постоянной скоростью v, то высота напора h, необходимая для преодоления сопротивлений движению на длине пути I, пропорциональна скоростной высоте J, пройденному пути I и некоторому коэфф-ту £, зависящему от свойств грунта водоносного пласта и от скорости v. Сказанное можно выразить ф-лой:

Коэфф. ξ м. б. выражен в общей форме так:

п < оо

V i^Pn

ξ=α

п> 1

(δ)

где а и β—постоянные величины, зависящие от свойств грунта водоносного пласта. Пренебрегая малой по сравнению с ‘‘ во-

личиной а и ограничиваясь первым членом бесконечного ряда, мы можем формулу (4) заменить формулой:

(6) (V)

где

(aVv + β j-

Из формулы (6) определяем скорость движения грунтовых вод:

В общей форме закон сопротивления движению грунтовых вод выразится, по Смре-керу, следующими уравнениями:

^l=а v³ + b v^m (9)

j=/с v^m; (10)

в этих уравнениях а —, Ь=;f, к =,

m=2 —* и варьирует в пределах от 1 до 2.

Если в особых случаях желательно получить более точные значения величин, чем при принятом т=^а„, то экспонент (показатель степени) т может быть определен опытным путем.

Определение экспонента т. Если принять за ось ординат Г—ось бурового колодца, а за ось абсцисс X—линию, лежащую в плоскости соприкасания водонепроницаемого слоя с водяным пластом, и определить точки A^x^yJ, А₃(х_г,у,), А₃(х₃,у₃) депрессионной линии, получаемой при определенной откачке воды из колодца, то на основании (10) получим ур-ня:

а) для точек А₃ и А,:

б)

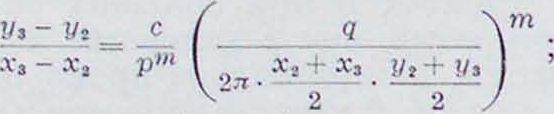
для точек А., и А,:

(И)

Vt~ У _С_ Х_% - Χι Р^т

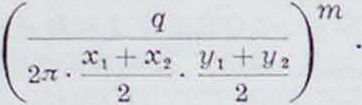
(12)

Решая эти два последние ур-ия по экспоненту т, получим:

и, - V,

Уг - !Л h,. - .V,

lg [(X. 4- “,)(!/, +у,)] - lg [(Х₂+Х»)(У, + У,)]

(13)

Количество грунтовой воды, протекающей по водоносному пласту. Если обозначить через Q количество грунтовой воды, протекающей по водоносному пласту с поперечным сечением F, а через р — пропускную способность грунта, то

Q=р F г, (14)

где г — средняя действительная скорость грунтовой воды. Подставляя в формулу (14) величину V из ф-лы (8), получим:

Лит.: В e g е г К., Vcrsuche г. Bestimmung d. Was-serdurchlassigkeit v. Sand, «Bauingenieur». И. 1922, В. 3. p. 680; Forchheimer Ph., Praktische Hi-draulik. Lpz., 1914; Forchheimer Ph., Zur Theorie d. GrundwasserstrOmungen, «Sitzungsborichte d. K. Akad. d. Wiss.», Wien, 1919, B. 128, p. 1223; Hand-buch d. Ingenieurwiss., T. 3—Der Wasserbau. B. 1—Ge-wSsserkunde. 5 Autl., Leipzig, 1 923; KcilhackK., Lehrbuch d. Grundwasser- u. Quellenkunde, 2 Aufl., B. 1917: L u in m crt R., Neue Methoden d. Bestimmung der Durchlassigkeit wasSerfilhrender Bodenscliichten. Brschw., 1917; Sinreker (). Bestimmung d. Durch-llussmenge v. Grundwasserstrilmcn. «Journal f. Gas-beleuchtung und Wasserversorgung», Miinchcn—Berlin, 1918. p. 281. С. Брилинг.