> Техника, страница 41 > Движение поезда

Движение поезда

Движение поезда (дифференциальное уравнение). Поезд, состоя из локомотива и вагонов, в общем представляет систему твердых тел, соединенных частью жесткими, частью упругими связями. Одни тела, как кузова, имеют лишь поступательное движение; другие тела, как скаты, имеют и поступательное и вращательное движение. При своем движении вся эта система ограничена упругим рельсовым путем, к-рый м. б. расположен на разных уровнях по длине поезда. Теоретически составление ур-ня движения системы тел но той или иной траектории под влиянием определенных сил возможно, но в общем виде такое ур-ие представилось бы необычайно сложным; поэтому необходимо сделать некоторые допущения, возможные в пределах точности подсчета, а именно, принимается: а) что весь поезд сосредоточен в виде математической точки в ц. т. поезда, б) что все силы приложены в этом ц. т. и в) что рельсовый путь представляет собою жесткую математическую линию. Опыт показал, что для практики эти допущения вполне приемлемы. При движении поезда к системе тел, в пего входящих, приложены следующие силы: 1) F_k—касательное усилие локомотива, приводящее поезд в движение; 2) lE_t—сила общего сопротивления всей системы; 3) реакции между скатами и рельсами и 4) реакции между отдельными единицами системы. При движении поезда можно применить теорему живой силы: dT - d где Т — ра бота, v—скорость, ш—масса. Работу совершают только силы F_kи W_k, т. к. реакции между скатами и рельсами приложены в мгновенном центре системы и, следовательно, их перемещения равны нулю, а реакции между отдельными единицами взаимно уравновешиваются. Обозначим элементарное перемещение через dS тогда элементарная работа сил, приложенных к поезду, выразится ф-лой (F_k — 1Г_А.) dS. Приращение живой силы определится следующим образом. Пусть т_к— масса единицы системы, имеющей лишь поступательное движение, т,.—масса полуска-та, имеющего и поступательное и вращательное движение, v—скорость движения, ω — угловая скорость ската, I — полярный момент инерции полуската, R—радиус ската. Живая сила поезда выразится суммой:

ZmjcV“. Irnc-V“. Σ/· to*

о * о ¹ о

Т. к. 2т_к + Хт_с=М (где М—масса всего поезда), а ω=-”, то живая сила поезда равна (м + 2 д.) ζ> или (1 + у) М ~, где у— поправка на инерцию вращения колесных скатов, то есть

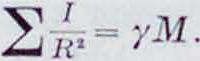
Приращение живой силы, т. о., примет вид (1 + y)Mv dv, и получается ур-ие: сF_t - W_k) dS=(1 + y)Mv dv.

Так как dS=v dt, то после преобразования получаем:

dv ₌ Fk - Wk

lit (1 + Υ)Μ

Если P—вес локомотива (в частности паровоза с тендером) в m, Q—вес состава поезда в m, a F_k и W_k выражены в килограммах, то

М=?±* 1000 о ·

F*-Wk

, „ P-rQ

(l-T У) ——1000

t- Fk - Wk ^ζ P bQ

где g равно ₍₁ - _у®₁₀₀₀, а g есть ускорение силы тяжести.

Ур-ие этого вида и носит общепринятое название д и ф ф ерей ц и а л ь и о г о ура в-н е и и я д в и ж е и и я поезд а. Необходимо оговориться, что касательная сила тяги паровоза непостоянна за один оборот колеса, так как индикаторное давление пара в разных положениях поршня неодинаково; поэтому F_k должно представлять собою среднее касательное усилие за один оборот колеса локомотива. Такая же оговорка справедлива и по отношению к W_k.

Дифференциальное ур-ие Д. п. позволяет решать ряд практических задач. Так как в общем виде

b-М и W_k=<p(v),

то путем интегрирования можно определить иек-рые зависимости. Представив дифферен-циолыюе ур-ие Д. п. в виде и интегрируя его, получим зависимость скорости от времени: v=F](<)·

Из ур-ия V=получается,чтоdS= F^fldt.

Интегрируя последнее ур-ие, получаем зависимость времени от пути: i=F₂(S). Для определения изменения скорости от пройденного пути уравнение можно представить в таком виде:

dv dv _; Fк - И*

dt ~ its ~^ς P + Q ’

откуда dS=[_Vk, T. e. v-~F₃(S).

^i_P + Q

Ньшеденное дифференциальное ур-ие Д. π. позволяет так.обр. решить ряд задач: определить время хода поезда, установить скорость поезда в любой точке, вычислить путь, необходимый для развития скорости до определенной величины, рассчитать вес поезда и т. д. Возможны ташке решения различных тормозных задач: при силе торможения В_к, уравнение получает вид:

dv _ Fk - И’* - Вк dt ^{= s} P+Q

Дифференциальное ур-ие Д. п. позволяет также исследовать вопрос о влиянии длины поезда при переменном профиле.

Величина у для нашего подвижного состава м. б. принята равной: для паровозов 0,06, для полногрузных товарных вагонов 0,04, для порожних 0,12 и для пассажирских вагонов 0,04. При таких значениях у, величина ξ колеблется в пределах 114—124 и, в среднем, может приниматься равной 120 (при исчислении ν—в км/ч, t—в ч,F_k и W_k— в килограммах, Р и Q—в яг). Аналитическое решение уравнения требует довольно сложных выкладок; обычно применяют различные приемы приближенных вычислений, а также приемы графич. решения.

Лит.· Ломоносов Ю. В., Тяговые расчеты. 3 изд., Берлин. 1922; Воскресенски it В. Д. я Б у д а н о в Д. Д., Проблема профиля и трасы жел. дорог. Москва. 1919; В я з е м с к и ii В. О. Тяговые расчеты и графики движения. II., 1918; Штанге ,1. А., Пособие для производства тяговых расчетов, М., 1926; К г о р ч е к к о В. Ф. Тяговые расчеты. Справ, руководство, Берлин, 1922; Л и пе ц Λ. II. Упрощенные приемы расчета времен хода поездов, СИВ, 1914; С у п р у к е н к о II. М., Тяговые расчеты. Киев, 1926; О п п е и г е ή м К. А., Проектирование ж. Д. 2 над. М. 1928. М. Федоров.