> Техника, страница 42 > Деформация

Деформация

Деформация, изменение формы упругого тела, вызываемое действующими на него внешними силами, если для тела устранена возможность перемещений, свойственных абсолютно твердому телу. Деформация упругого тела будет определена, если будут известны для каждой его точки проекции U, V и W ее перемещений на координатные оси. Если предположить, что упругое тело закреплено в начале координат и лишено возможности вращения относительно координатных осей, то, при действии на него растягивающей

19

Т. Э. m. VI.

силы по направлению оси X, перемещение любой точки тела с координатами х, у, г выразится величинами:

U — ix, V=— угу, W=— yiz, где г—относительное удлинение, η—коэфф. Пуассона поперечного сжатия при растяжении или сжатии, свойственные данному упругому телу. Т. о., координаты той же точки после растяжения будут:

= д(1 + г). Vi =2/(1-Ч*)» z₁=z(l-yi).

Так, если упругое тело до Д. имело форму шара с ур-ием поверхности .г·² + у² + г²=г¹, то после Д. оно получит очертание по поверхности с уравнением:

I___У) 4. ^z=_Г2

(1 + i)¹ (1 - тУ ^τ (1 - тУ ’

то есть получит форму эллипсоида. Рассмотренный случай Д. при растяжении представляется линейной функцией координат и называется однородной Д. В общем случае Д. представляется сложной функцией от координат; но если рассматривать только малые Д., как это имеет место во всех технич. задачах, то квадратами перемещений и их производных по координатам можно пренебречь; при этом предположении относительные перемещения будут выражаться линейными функциями относительно координат, что позволит считать Д. однородной в пределах малого объёма, заключающего рассматриваемую точку тела.

Д. в рассматриваемой точке тела будет вполне определена, если будет известно изменение длины какого-либо линейн. элемента А, проходящего через эту точку. Она выражается при посредстве след. 6 величин:

_ ди _ оу _ ow ^е“ ~ дх ’ ^еУУ ~ Оу ’ ^е-^{2 =} дг ’

(1)

представляющих собою относительные удлинения по направлению координата, осей, и дУ дУ 0U, 0W

^е*у~ Оу ⁺ дх > дг ⁺ дх ’ _/1оЧ

_ dV 0W

^еуг ~ дг ду ’

представляющих собой относительные сдвиги, соответствующие осям ΧΥ, ΧΖ и ΥΖ. Общий вид уравнения удлинения любого линейного элемента

^ех ~ l^exx + ^т2ет + ⁿ*^ea + у +

+ mne_yz + Ine^. (2)

В этом ур-ии величины I, т и п соответственно равны косинусам углов наклонения элемента А к осям X, Y и Z координат. Величины е_хх ,.,е,_/2 носят название слагающих Д. в данной точке. В случае однородной деформации эти величины постоянны ио всему объёму тела. Они являются известными функциями перемещений U, V и W. не м.б. произвольными и связаны между собой следующими дифференциалы!, зависимостями:

дЧ гг. двуу _ дс.гу О у‘ ¹ Ох- ОХОу в в., О··.- двх!

дг“ ’ дх^{1 =} дхдг

^йЧУУ J- ^Э’⁶^ ₌ ^д‘^е!/г дг“ ду“ Oyoz

(3)

9 д * Βχχ ^ Oyoz

9 д“^еуу

~ dxdz

_ д /_дсу“ i де_:х, де_хц дх дх ‘ ду ‘ Oz )

__ д {_ д^erz j_ ®^ету I де^_г

~ ду ду ¹ дг дх)

о ^a*^e~=^0де*У j_ ^деУз _i_ дудх дг дг ‘ дх ‘ ду I

(За)

Эти зависимости представляют собой вторые производные от составляющих Д.; поэтому в тех случаях, когда последние постоянны по всему объёму, они всегда будут удовлетворены. Если откладывать по направлению линейного элемента А соответствующую ему Д. в виде отрезка г =- ^h, то концы этих

V «я отрезков расположатся но поверхности второго порядка, которая носит название п о-верхности Д. Уравнение этой поверхности получится, если в выражение (2) подставить вместо величин I, m и п их выражения через г и соответствующие координаты: е_хх х^г + е_уу у ‘- + е_а · г² + е_ху ху + е„ xz + + · ψ=t к“. (4)

Координаты осей всегда м. б. выбраны так, чтобы члены, содержащие произведения координат, исчезли, то есть так, чтобы углы между осями координат не деформировались. Д., соответствующие такому направлению осей, называются главны м и и а п р а в-лениями Д., а соответствующие им удлинения—г л а в н ы м и у д л и и е н и я м и (е_п, е₂₃, е₃₃). Если оси X, Y и Z совпадают с главными направлениями, поверхность Д. определяется ур-ием:

г_и.г- + г, ге₃₃г-= i к·. (5)

Т. о., если известны главные направления Д. и соответствующие им относительные удлинения, то этим вполне определяется Д. в рассматриваемой точке. На основании закона Гука (1676 год) принимают, что между слагающими напряжений: нормальными п„. m_w, w., касательными /«=««.,

t_y.=i_zy и слагающими Д. е_хх,. е_уг в каждой точке тела имеется линейная зависимость, которая в общем виде выражается так:

^l^xx—OixG_xx- -c_i‘_ie_yy- -c₁^c_zz- -c-_iic_jy- -Ci_ttc_xz- -c^c_yz |

;;;;;;;;;;;;;;;;;;;;;;; кв)

(.ус ~ б₆₁с_хх-{-с_бзСуу-|-с_Сзс-_г4-с_е4с_:Г2_/4- с_йге_у: j

В эти выражения входят 30 постоянных величин (с_п, ., с_вв), характеризующих упругие свойства тела и называемых упругими постоянными. В теории упругости доказывается, что между этими постоянными существует 15 зависимостей вида c„_m—c_m„, что уменьшает число неизвестных постоянных до 21. В телах изотропн ы х, то есть имеющих одинаковые упругие свойства во всех направлениях, происходит дальнейшее сокращение числа упругих постоянных, вследствие обращения некоторых из них в нули и равенства других между собою. Если принять, что в изотропном материале (например, в стали) направление главных напряжений в каждой точке совпадает с направлением главных Д. (положение К о ш и), то зависимость между напряжениями и Д. в этом случае будет выражаться при посредстве двух упругих постоянных, и полное изменение формы выделенного элемента будет определяться 3 слагающими е_1Х, е_т и e._z. В конечном преобразовании эти зависимости приводятся к виду:

Пхх

^пуу

К«т + е_т + О + Ке_хх + е_т + e_t.) + 2 με К^ехх + R_yy + с_;г) + 2/<е. Vy ⁼ /^<е*у

!‘^ехг

XX

УУ

уз

В этих выражениях λ и μ—коэфф-ты (предложение Lam6). В технике вместо этих коэффициентов обычно пользуются модулями упругости: продольной Е и поперечной G, а также коэфф-том η Пуассона, выражая эту зависимость так:

Εη

(1 + 4)0 - 2η)

μ=0

E

2(1 +η)

(8)

Подставив эти значения в выражение (7), получим:

^хс j , [ C₁-χ + j 2^ (^зяс Г С./,у + C₂s)J

^ИУУ ~ 1 + I) [ ^еУУ + Г- 2>) ^СУУ ^C”-*J

ⁿzz=J^T₄ [^егг + рГЛГ, (^βτχ + ^eyy + ^егг)]

(9)

^xy 2(1 + у) ~ Gc_Xy, t_xa Ge_xs, ty_S GCy_S)

Величины же слагающих Д. выразятся так:

<Дг=1· [n_CT-r,(M_w-)-wj]

C₁/,y ⁼ j, [ Ί" ^гг) j

e2*=[n„ - r,(n_n + n_xx) ]

При решении технпческ. задач о величине и распределении напряжений в упругом теле приходится определять их по заданным внешним силам. Шесть слагающих напряжений в любой точке тела связаны между собой, как известно, следующими тремя дифференциальными ур-иями равновесия:

<*il_rr t - dt_Xz

()X uy bz

d_ⁿyy i QUjx I dty: dy ~ dx ilz dn_Zz, dt_lx, 91-j, Oz "i* dx ‘ dy

+x»=o

+ i_r=0 + Z_C=0

(11)

в которых X_r, Y_r и Z,—слагающие объёмного веса. Этих ур-ий, как известно, недостаточно для определения напряжений. Но т. к. вызываемые этими напряжениями Д. должны удовлетворять шести дифференциальным зависимостям (3) и (За), то, с присоединением их к ур-иям (11) и составлением условий равновесия на поверхности тела, получится достаточное число условий для определения слагающих напряжений. Зная последние и пользуясь выражениями (10), можно определить величины слагающих Д. (е_ХТ, ., е,_г), после чего задача сводится к определению перемещений U, V и W, что может быть выполнено путем интегрирования системы линейных уравнений (1) и (1а). Проведение этих расчетов относится к задачам теории упругости.

Плоская задача. Д. называется плоской, если перемещения всех точек тела параллельны одной и той же плоскости. В этом случае перемещения U и V будут ли нейными функциями координат х и ?/, а перемещение W— 0. В частных случаях возможно наложение условия действия но направлению оси Z равномерного растяжения или сжатия, в каковом случае перемещение W будет линейной функцией от г. К такому виду плоской Д. приводится большое число технич. задач, в которых длинное тело можно рассечь параллельными плоскостями на отдельные элементы, находящиеся в одинаковых условиях Д. В связи с таким предположением будет иметь место ряд упрощений, а именно: 1) слагающие напряжений t„=0 и t_yz= 0; напряжение п_:, или равно 0 или м. б. выражено в функции п_хх и п_уу; 2) слагающие деформаций е_хг=0 и е,_/г=0; слагающая Д. е,_г или равна 0 или представляется постоян. величиной. Соответственно этому: а) дифференциальные уравнения равновесия (11) приводятся к двум уравнениям:

л. χ ₌ о- ^0пиу i ^д1ух i у _ о · ПФ дх ^ оу ^ “’ ду ^ ох л б) кроме того,

v(n_xx + Пуу);

в) дифференциальные зависимости (3) между соответствующнмиД.приводятся к одной:

Уе-rr, д^ет _ °^ету /|о ду^г ‘ ох‘ охОу *

Остальные зависимости тождественно удовлетворяются; величины (10) слагающих Д. приводятся к виду:

^ехх=£ (^пхх — ЧИуу) 1 ^еуу ^г= ~щ (^пуу ~ ^г1^пхх) ’>

_ 2(1+4), __1, (И)

Сгу- £ ^lxy— G -у

Такие же упрощения получаются, когда упругое тело представляется в виде тонкой ци-линдрич. пластинки, толщиной 2h. Для срединной плоскости .ХУ такой пластинки слагающие напряжений п_хх и п_ю определяются ур-иями вида (12); что касается величины напряжения п_гг, то, т. к. оно по крайним плоскостям пластинки равно 0, его с достаточной степенью точности можно принять равным 0 по всей толщине тонкой пластинки.

Переход от пространственного упругого тела к плоскому позволяет применить для изучения распределения Д. и напряжений оптический метод. Начало метода можно видеть в опытах Брюстера (1815 г.), который показал, что нек-рые изотропные аморфные тела, обычно оптически постоянные по всем направлениям, под действием внешних сил,т.е. под влиянием происходящих при этом Д., временно изменяют свои оптическ.свойства и становятся, как говорят, д в у п р е л о м л πιο щ и м телом, то есть обнаруживают в поляризованном свете явления хроматической и о л я р и з а ц и и.

Предположим, что на прямоугольную стеклянную пластинку, находящуюся под действием равномерно распределенных по ее граням давлений п_и и п.,₂(фигура 1) падает поляризован, луч света DD с

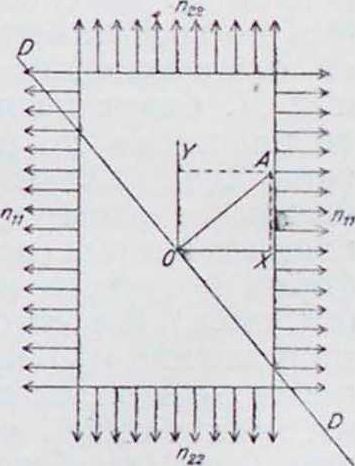
Фигура I.

Хроматически ii м а с ш т а б н а п р я ж е и и ii для к с н л о н и т о-в о г о (целл юл оидного) образца, толщ. 6 миллиметров, сечением 60 миллиметров³.

Поря док	Цвет окраски	кг/см“	Поря док	Цвет окраски	кг!
	Собственный цвет			Оранжевый.	143
	черноватый.	—	III	Пурпуровый.	158
I	Сероватый.	13		Фиолетовый.	168
	Бе лопаты it.	23		Голубой.	171
	Белый.	26		iч>лубовато-зеленый.	186
	Желтопато-белый.	36		Зеленый.	193
	Желтый.	63		Желтый.	216
	Коричневатый.	76		Красный.	230
	Оранжевый.	78	IV	Пурпуровый.	236
II	Пурпуровый.	SO		Серовато-голубой.	246
	Фиолетово-голубой.	87		Голубовато-зеленый.	250
	Индиго.	93		Зеленый.	258
	Голубой.	103		Желтовато-зеленый.	27К
	Зеленовато-голубой.	118		Красный.	290 ;
	Желтовато-зеленый.	123	V	Серо-голубоватый.	313 *
	Желтый.	135		Зеленый.	320 1

колебаниями, направленными по О А. Как только под действием внешн. сил в пластинке возникнут неодинаковые деформации по направлениям×и Y, распространение световых колебаний по этим направлениям будет происходить неодинаково, и пластинка станет двупре-ломляющей, вследствие чего плоскополяризован-ный луч разложится на два взаимно перпендикулярных колебания. Т. к. скорости v_x и v_y распространения колебаний будут неодинаковы, то после прохождения луча через пластинку толщиной с будет получаться разность А хода обоих лучей, пропорциональная произведению разности скоростей (v_x— v_y) на пройденный путь:

Δ=· c(v_x - v_y),

где k_l—постоянная величина, не зависящая от свойств материала. Чем больше будет разность скоростей, тем больше будет разность напряжений и соответствующих им Д., а потому

ν_χ-υ_ν= fc₂(n_u-w₂₂); отсюда следует, что

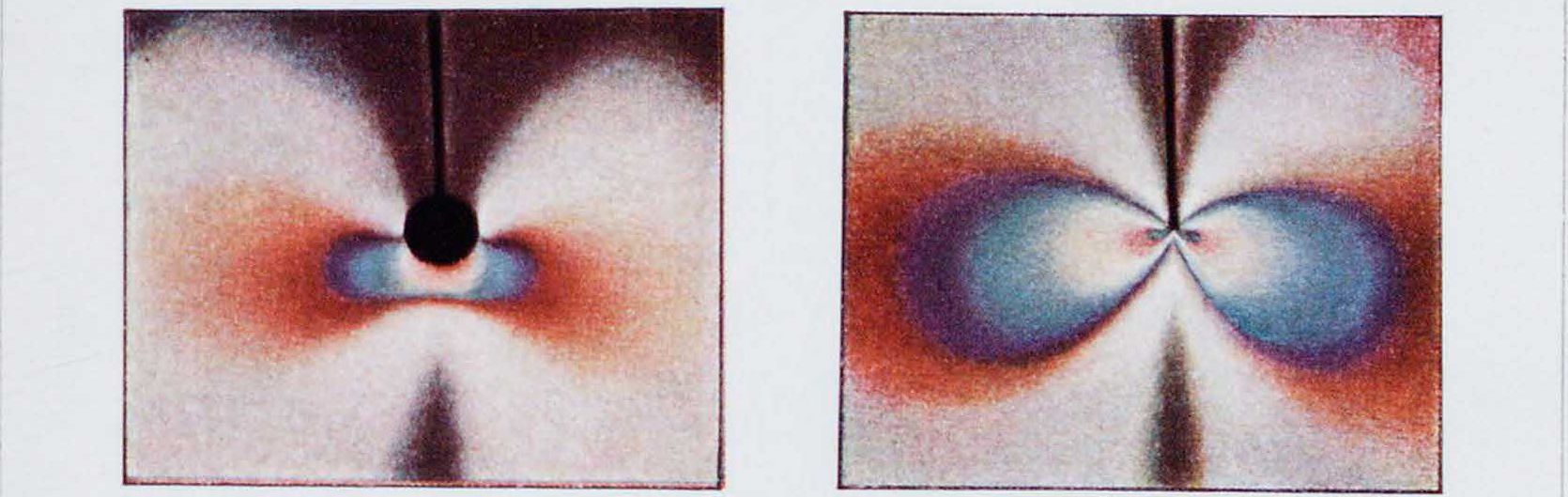
Δ= fcj. fc₂ · c(n_u-n₂₂), и где /. — коэффициент оптической упругости; он различен для разных материалов (для стекла принимают к равным 40 000 килограмм/мм²). Т. о., запаздывание в лучах будет характеризовать разность главных напряжений (п_ет — Пуу) и, следовательно, будет определять величину наибольшего касательного напряжения: t=¹/₂(n_ll—n₂₂). На анализаторе, воспринимающем на себя пучок поляризованных лучей, пропущенных через испытуемую пластинку, это явление запаздывания будет характеризоваться появлением окрашивания пластинки. В зависимости от распределения Д. пластинка будет окрашиваться в различные цвета; в случае однородной Д. изменение цвета будет одинаковым по всей пластинке; если в зависимости от односторонних или местных нагружений Д. будут распределяться неодинаково по пластинке, то распространение окрашивания будет характеризоваться различными цветами, которые будут распределяться в виде цветных кривых (радуг или колец Ньютона), форма и густота которых бывает различна (смотрите табл.). 13 частном случае, когда главные напряжения п_п—п_п, разность между ними равна нулю, и, следовательно, Д. будут равны между собой, разности в распространении лучей не будет, а потому и не будет окрашивания. Т. о., применение поляризационного метода для изучения пластинок, подвергающихся напряжению, позволяет непосредственно установить распространение Д. и напряжений в испытуемом образце. Преимущество его заключается в том, что он дает возможность выявить картину распространения напряжений и Д. для таких сложных моделей, для которых теоретич. решение или затруднительно или даже невозможно. На вкладных листах дан ряд цветных фотографий, показывающих распространение Д. и напряжений в различных моделях. Этот метод м. б. использован также для определения величины разности главных напряжений. Для этого достаточно рядом с испытуемым образцом поместить эталонный стержень из того же материала и подвергать его равномерному растяжению с измерением действующей на него силы. Сопоставляя изменение цветов этого эталона при различных напряжениях в нем с цветами на испытуемом образце и следя не только за цветом, Ηό и за его порядком, можно с достаточной степенью точности определить количественное распределение напряжений.

Оптическ. метод позволяет рассматривать распределение Д. только в условиях плос-ской задачи. По именно то обстоятельство, что при рассмотрении, в условиях плоской задачи, простых (односвязных) контуров распределение напряжений в пластинке, как показал М. Леви, не зависит от упругих постоянных Е и η, придает большое значение этому методу, т. к. устанавливает возможность изучать любые модели из прозрачных материалов, необычных для этих моделей, с полной уверенностью в том, что при изготовлении этих моделей из стали и др. изотропных материалов напряжения в них будут распределяться так же, как и в прозрачных материалах. И. Мишель показал, что в случае многосвязных контуров распределение напряжений не зависит от упругих свойств материала, если внешние силы, приложен, к каждому отдельному контуру, представляют систему сил, взаимно уравновешивающихся, или систему, приводящуюся к паре.

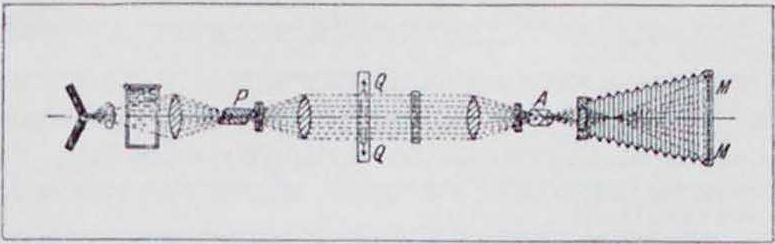
Для оптич. исследований применяют специальные приборы, изготовляемые оптич. фирмами. На фигуре 2 показана схема установки Цейсса; в основе она состоит из двух скрещенных призм Николя — поляризатора Р и анализатора А, между которыми помещается испытуемый образец в прессе Q; изображение получается на плоскости ММ в особой камере. Более простую и легко выполнимую конструкцию представляет уста-

1. Траектории касательных напряжений при изгибе балки (вверху уточки приложения груза влияние местных нагружений). 2. Простое растяжение. 3. Сжатие цилиндра. 4. Схема распределения напряжений, возникающих при прессовании. 5, 11, 12. Схемы распределения напряжений при прокатке. 6, 7,8,9, 10 и 13. Распределения напряжений, наблюдаемые в различные моменты прокатки.

РЕФОРМАЦИЯ

14

15

16

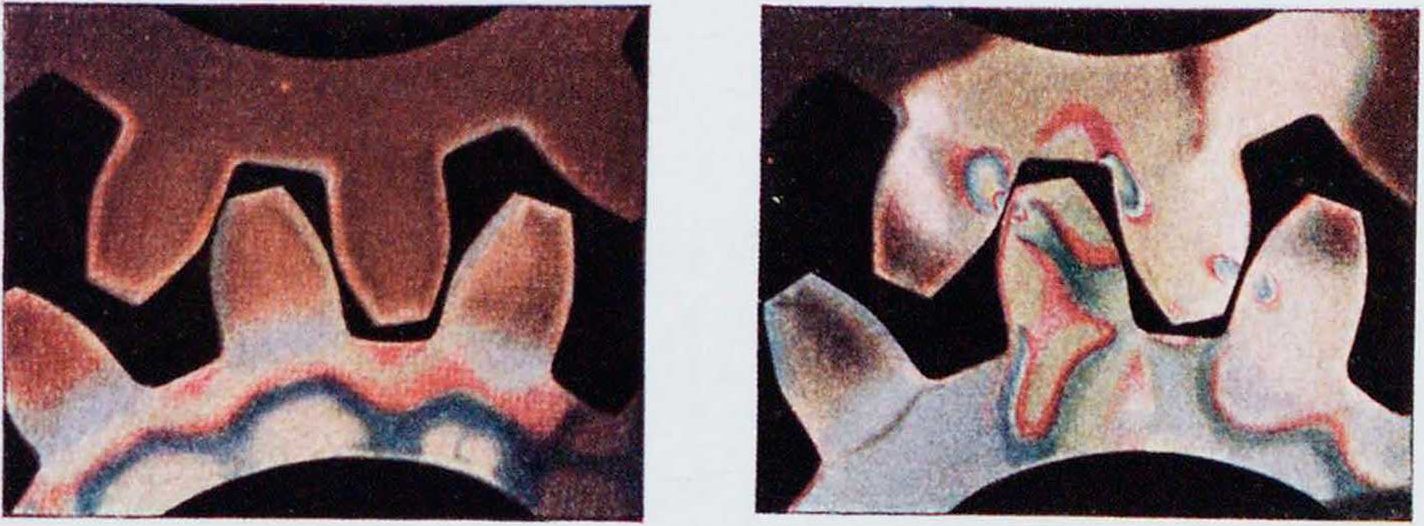
14. Влияние отверстия на распределение напряжений при растяжении. 15. Напряжения в конце трещины растягиваемого прямоугольного бруска. 16. Влияние круглого отверстия в конце трещины растягиваемого бруска. 17. Распределение напряжений в шестерне, насаженной на вал. 18. Распределение напряжений в шестерне под действием вращающего момента.

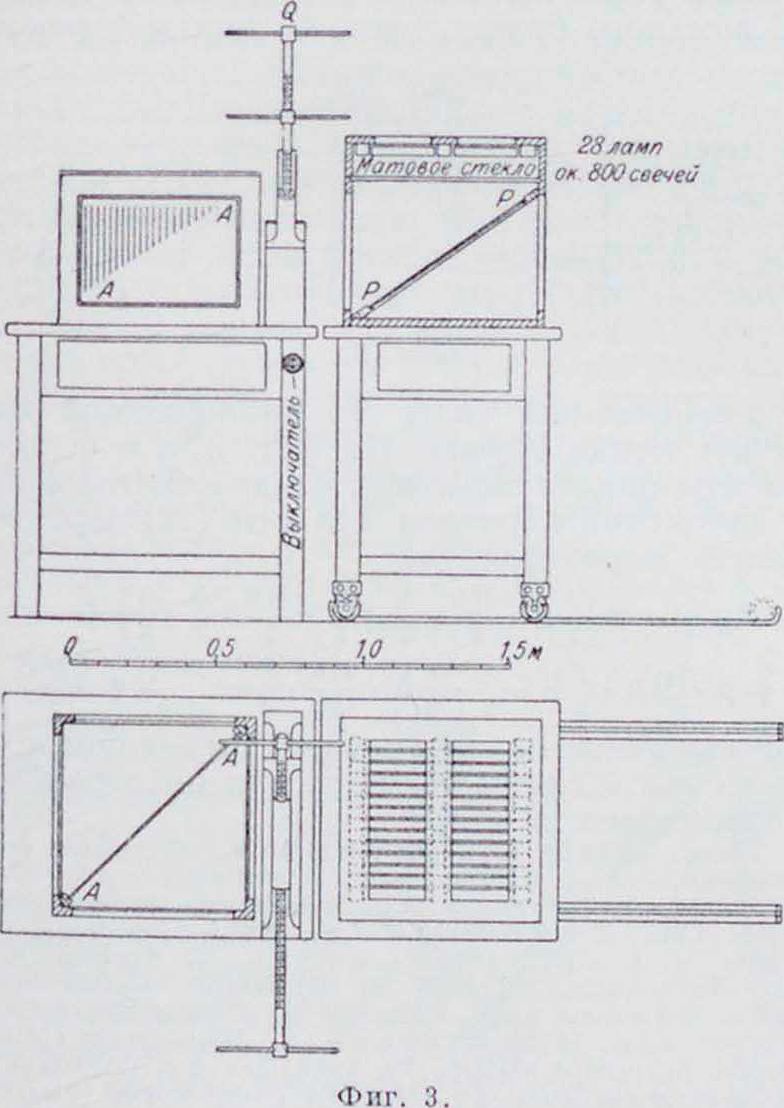
новка Кирпичева и Зайцева (фигура 3). Она состоит из 2 марблитовых (зачерненных) зеркал, из которых зеркало Р воспринимает свет от электрич. лампочек и отбрасывает его в виде поляризованвого пучка, проходящего

Фш·. 2.

через испытуемый образец, помещенный в прессе <3; второе зеркало А служит анализатором, в к-ром отражается деформированный образец. Обычно испытание производится над образцами из стекла или ксилонита. Лучшим из них является последний, т. к. не будучи столь хрупким как стекло, он обладает лучшей двупреломляющей способностью,так что пригоден для опытов уже при толщине 2—3 миллиметров; кроме того, он легко подвергается обработке лобзиком и стамеской.

Определение Д. в брусьях и стержневых системах. В повседневных задачах техники приходится иметь дело преимущественно с брусьями и стержнями, то есть с элементами, имеющими небольшие поперечн. размеры по сравнению с длиной; такое соотношение размеров позволяет

пренебречь влиянием поперечных Д. и рассматривать брусья и стержни как состоящие из бесконечно малых элементов длиной ds с постоянным поперечным сечением. При этих условиях вывод общего выражения Д. или перемещения можно сделать, исходя из начала возможных перемещений, согласно к-рому работа сил, приложенных к находящейся в равновесии материальной системе, на любых бесконечно малых возможных перемещениях равна нулю, следовательно, в упругих системах сумма работ внешних и внутренних сил равна нулю. В общем виде работа внешних сил м. б. представлена в виде произведения ^S_kS_k, в к-ром под S_k подразумевается любая внешняя сила, пара или момент, а под д_к—соответствующее им линейное или угловое перемещение. Работа внутренних сил м. б. выражена через слагающие внутренних сил, приложенных к любому бесконечно малому элементу длиной ds и определяемых величинами: нормальной силой N, поперечной силой Q и изгибающим моментом М, и через соответствующие им деформации: продольное удлинение Λ ds, поперечный сдвиг Ady и поворот сечения при изгибе Αάφ. Исходя из принципа независимости сложения действий, работу внутренних сил для любого бесконечно малого элемента можно выразить так:

(IT=NAds + QAdy + ΜΑΛψ,

а для всего тола она определится интегралом из этого выражения. Т. о., исходя из условия равенства нулю суммы работ внешних и внутренних сил и учитывая, что работа внутренних сил противоположна по знаку работе внешних сил, можно написать, что:

f Al_kAds + J Q_kAdy -j- J M_kAd<p. (15)

Если деформации вызваны приращением какой-либо внешней силы S_m, то величины Ads, Ady и Αάφ для каждого бесконечно малого элемента выразятся так:

Ads=ds, Ady=к ^C;^m ds, Αάφ=%gds,

где J и ω соответственно—момент инерции и площадь сечения, к—коэфф., зависящий от формы сечения (в прямоугольных сечениях к=®, в круглых—fc= ^. Если Д. вызвана изменением темп-ры, то Ads— at₀ds, А άφ=α ds, где t₀—темп-pa осевого волокна элемента, равная .(<,+ t,), и At—разница температур крайних волокон, равная(i,—L); с—толщина сечения. Подставив эти выражения Д. в формулу (15), получим:

2^SA,„=f N_k?*ds+al₀f N_tds+k f Q*§s«te+

+ f Mk EJ ds + f M_k -y ’ (10)

где S_km—перемещение S_k под влиянием изменения S_m. Когда рассматриваются Д. в сочлененных системах (фермах и т. и.), в которых внутренние силы определяются только продольными усилиями N, а площади поперечных сечений по длине каждого стержня обычно постоянны, выражение (10) приводится к такому:

Σ ^SAm=2 ^Nk t ^λ + Σ ^Nk°^a. (Π)

η котором λ—длина каждого стержня между шарнирами. Выражения равенства работ (10) и (17) не изменятся, если вместо ряда внешних сил будет действовать одна сила

S_k=1, вызывающая внутренние силы N_k, Q_k и момент М_к, но они приведутся к виду

*кт=f ^Nii ds + α£₀ jN_kds + к f Q_k g“- ds +

+ f M_k ds + aM f ψ ds, (18)

^-Σ^Ν^^λ+^α1Σ^· (^1<J)

В таком виде эти выражения известны под названием ур-пй Мора и служат для непосредственного определения перемещений, для чего в соответственных точках системы прикладываются по направлению искомого перемещения сила, равная 1,если определяется линейное перемещение, или момент, равный 1, если определяется поворот сечения, или, наконец, пара с моментом, равным 1, и плечом, равным длине стержня, если определяется поворот стержня. Эти единичные силы и моменты называются фиктивными,или воображаемыми, и служат только для определения перемещений. В тех случаях, когда определяется перемещение по направлению действующей силы или момента, для определения его удобно пользоваться теоремой Кастильяно, по которой перемещение определяется как частная производная из выражения потенциальной энергии по соответствующей силе или моменту:

Qk dQ_kG и

δ

f^-^dS + fc Г 5* · Щ* ds +

^,JC oSjt J hoi d&k J Goi dSк

+ 1£?-Щ^а*· (2°)

Нетрудно, однако, видеть, что это выражение представляет собой частный случай выражения (18), так как всегда можно представить, что N_k=N_k· S_k, M_k=M_k-S_k ит. д.,

ϋΝι ^

а потому величины производных _os*=N_k,

О М L

_oS~=M_k,., что приводит выражение (20)

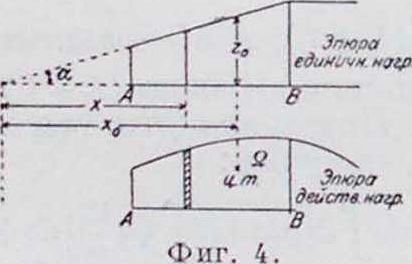
к виду (18). Обычно при вычислении перемещений пренебрегают влиянием поперечной силы Q на Д., т. к. оно незначительно по сравнению с влиянием продольной силы и особенно момента. Влияние Q нарастает с увеличением поперечных размеров по отношению к длине. В системах с прямыми осями (балки,рамы и т.п.) процесс интегрирования по ф-лам (18) и (20) с успехом м. б. заменен вычислением влияния моментов по их эпюрам, что м. б. сделано или приемом Мора—путем рассмотрения эпюры как фиктивной нагрузки, или приемом Верещагина—путем сопоставления эпюр действительной и единичной нагрузок. Эпюры единичных нагрузок всегда имеют очертания по прямым, наклоненным под углом а к оси стержня; эпюры от действительной нагрузки могут иметь криволинейное очертание. Для каждого прямого участка эпюры момент от единичной нагрузки всегда м. б. выражен через ординату эпюры г=х tg а, где х—расстояние ординаты от нулевой точки пересечения прямой, очерчивающей эпюры, с осью стержня (фигура 4). В соответствии

с этим, входящий в выражение (18) интеграл может быть приведен к такому виду:

- Т ]*("" dx).c. (21) Оставшийся под интегралом множитель ^Mj"- dx представляет собой элемент площади эшоры моментов от действительной нагрузки на участке dx, измененный в отношении 1 :</; при постоянном моменте инерции последний выходит за знак интеграла. Самое же произведение (^л^” dx)х представляет собой статическ. момент той же площади относительно нулевой точки единичной эпюры, а потому весь интеграл м. б. выражен в таком виде:

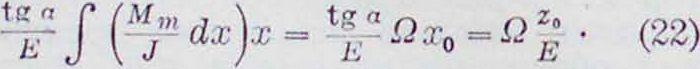
В этом выражении Ω—площадь всей эпюры момента от действительной нагрузки—изменена в отношении 1: J, acc₀tg а определяет собой ординату г₀ эпюры единичной нагрузки под ц. т. площади эпюры от действительной нагрузки. Т. к. в этом выражении перемещение определяется произведением площади на соответствующую ординату, то знак его определяется алгебраически по знакам эпюр. При ломаном очертании эпюры единичных нагрузок полное перемещение определяется суммой произведений Ωζ₀ каждого участка. Напр., пусть требуется определить горизонтальное перемещение точки К ломаного бруска (фигура 5) под действием

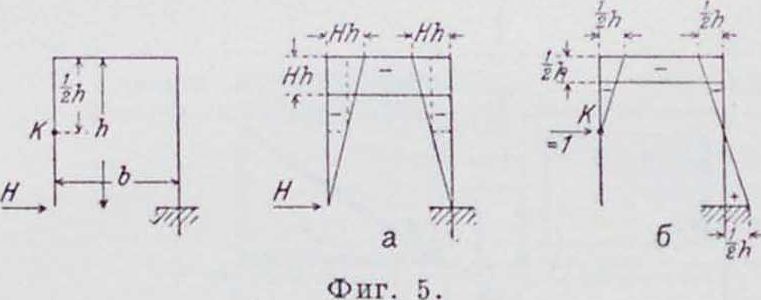
горизонтальной силы Н, приложенной на левом конце бруска. На фигуре 5, а и б, показаны эпюры моментов от действительной и единичной нагрузок. По ф-ло (22) перемещение выразится так:

h

¹кн

+ Ь

ΠΙι · ‘

II h	·:+;·	Ilh
2		2
1	1 ^ · ψ	h
2		’ 6 =

2

ЗН h-ΐβ

а+

+

bllh

Аналогичные приемы расчета по эпюрам могут быть сделаны также и для интегралов, содержащих N и Q.

Лит.: Общая: Ясинский Ф., Собрание сочинений, т. 3, СПБ, 1902; М и тине к И и Н., Строительная механика. Сопротивление материалов. СПБ, 1911; Т и м о ш е и ко С., Курс теории упругости, ч. 1, СПБ, 1914; Love Λ. Λ Treatise on the Mathematical Theory of Elasticity. Cambridge, 1928; Clebsch A., Theorie d. Elastizit&t fester KOrper, Lpz., 1862; Clebsch A., Th6orie de Г 61a-sticit6 des corps solides, P., 1883; Lame. Lcqoiis sur la thgorie mathiSm. de 1 6lasticit6 des corps solides, 2 6d., P. 18G6; d e S a 1 n t - V e n a n t, La resistance des corps solides. P., 1864; В о u s s i n e s q, Applications des potentiels ii 1’6tude de I’equilibre et du mouvement des solides eiastiques. P., 1885; N e u-m a η n I<, Vorlesungen uber die Theorie d. Elastizi-tiit d. festen KOrper und d. Lichtathers, Lpz., 1 89 Love A., Lehrbnch d. Elastizitiit, Lpz.—B., 1 907; T edone О. Allgemeine Theoreme d. mathem.Elasti-zit&tslehre (Intcgrationstheorie), Enzyklopiidie d.inath. Wiss.j B. 4, Abt. 2. H, 1, Lpz., 1907. Оптический м -тод: К и р п и ч е в В., Оптическое изучение упру-

πιχ деформаций, «Вести. ОС-ва технол.», СПБ, 1013; Оптич. метод определении напряжений, «Американ, тсхн.», Нью Морк, 1926. 7; 3 а и ц е в А. Оптичсск. метод изучении напряжений, Л., 1427; Maxwell on the Equilibrium of Elastic Solids. «Trans. Roy. Soc. Edinbuigh», Edinburgh, 1853, v. 20; Leger M. Transmission des forces extfirieurcs au travels des corps solides, «MOmolres et comptes rendus des tra-vaux de la Sociit6 des Ing. civils», Paris, 1 879, sfo ie 3, V. 12, p. 288—341; ill esiuger A., Contribution i l’fitude de la diformation Olastique des solides, <·Αη-nallcs des pouts et cliaussOes», Paris. 1901. sOrie 8, trim. 4. p. 135; Co ker E., The Determination by Photo-Elastic Methods of the Distribution of Stress, • Transactions of the Institute of Naval Archit.», London, 1911. И. Пронофьев.