> Техника, страница 43 > Динамика аэроплана

Динамика аэроплана

Динамика аэроплана, учение о движении аэроплана; если аэродинамика изучает возникающие при движении тела в воздухе силы, то динамика аэроплана, оперируя этими силами, находит движение, вызван. ими. Очень часто Д. а., в общем смысле, разделяется на несколько самостоят. отделов, изучаемых особо. Так, изучение прямолинейного установившегося полета и применение получен, результатов для конструирования аэроплана относятся к аэро-динамич. расчету аэроплана и к простейшей теории аэроплана; изучение устойчивости аэроплана в воздухе, его маневренности и управляемости обычно относятся к теории устойчивости (смотрите Устойчивость). К динамике аэроплана, в узком смысле, относятся некоторые вопросы прямолинейного установившегося полета, изучение взлета и посадки и, наконец, изучение различных криволинейных и неустановившихся полетов, к которым относятся фигурные полеты.

Математич. решение различных вопросов Д. а. производится, гл. обр., путем интегрирования основных дифференциальных ур-ий

движения аэроплана, которые, однако, в общем случае не интегрируются и ращению поддаются лишь в сравнительно немногих частных случаях и только после введения различных упрощающих условий. Надо заметить, что многие вопросы Д. а. далеко еще не разрешены, что весьма часто объясняется отсутствием аэродинамических данных относительно особенных движений крыльев и возникающих при этом сил. В виду того, что многие вопросы Д. а., например фигурные полеты, играют большую роль в практике и изучение их важно для установления соответствующих критериев для оценки качеств аэропланов, за последнее время началось более интенсивное экспериментальное изучение полета аэроплана как на моделях в аэродинамич. трубе, так и над аэропланом в натуру; постановка этих опытов, однако, связана с большими трудностями.

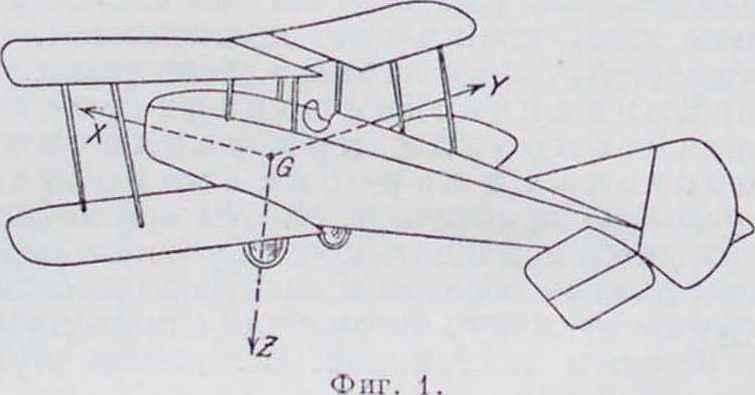
Движение аэроплана можно рассматривать как движение твердого тела в пространстве, причем положение его можно определять путем определения координат его ц. т. и путем ориентирования жестко связанных с аэропланом осей координат по отношению к координатам, связанным с воздухом, в котором движется аэроплан, или по отношению к координатам, связанным с землей—земным координатам. Обычно начало координат связанных с аэропланом осей находится в его ц. т., причем ось×направлена по продольной оси инерции аэроплана, а оси Y и У. соответственно по поперечной и вертикальной осям (фигура 1). По отношению к воздуш-

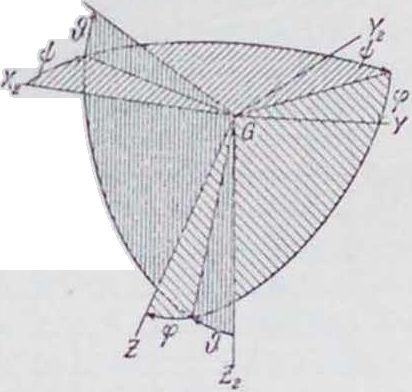
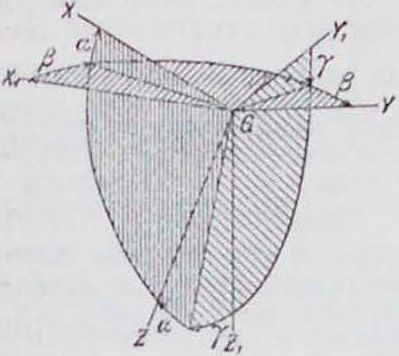
ным координатам наклон аэроплана определится углами а, β и у, т. н. углами встречи, сноса и крена (фигура 2). Если же относить аэроплан неземным осям», то, в зависимости от того, в какой последовательности вращать аэроплан около его осей, получится и соответствующее ноло-жение его в пространстве. Будем обозначать через у угол вращения аэроплана около оси Ζ, через ϋ—угол вращения аэроплана около нового положения оси У и через φ—угол вращения около последнего положения осп X^м, эти углы называются соответственно углами рысканья, тангажа и крена (фигура 3).

Пусть V есть скорость аэроплана по траектории; обозначим через v_y, v. проекции этой скорости на связанные оси координат. Эти компоненты скорости выразятся след, ур-иями: v_x — v cos a ccs β, v_y=— v sin β, v. - - v sin a ces β;

скорость г будет через них выражаться так:

Ф и г. 2.

v — γυ% + vf, + г?.

Обозначим через р, q, г угловые скорости вращения аэроплана соответственно около связанных осей X, У, Z, через X, У, Z проекции внешних сил на них, а через L, Μ,Ν—моменты относительно тех же осей, действующие на летящий аэроплан; тогда (i следующих дифференциальных уравнений и выразят собой движение аэроплана:

т + v_xr - r.p) - Y

^т(^пщ+^г!/Р-ад)=²

dh, „i, г

- ph, + r)_h=Μ

-ϊί-qK+ph^N

где

h_l=рЛ — cjF — rE 1

h,=qJ3 — rD — pF J (Г)

h₃=rC — pE — qD i

а А, П, C, Ώ, E и F—моменты инерции и центробежные моменты инерции аэроплана. Центробежные моменты D и F вследствие симметрии аэроплана относительно плоскости XZ равны нулю, и выражения (1) будут иметь вид: hj^—pA — гЕ h.,= qB; li^—rC — pE.

В выражения Χ,Υ,Ζ входит также и сила тяжести. На фигуре 3 указаны расположения углов & и <р при соответствующих поворотах аэроплана. Т. о., углы между связанными и земными осями выразятся уравнениями:

cos XGZ_t=— sin ft, cos YGZ,=cos & sin φ, cos ZGZ]=cos # cos ψ.

Тогда общие уравнения движения аэроплана будут иметь вид:

т (ft -f- v.q — v_yrj=— mg sin & +×m + v_xr — Vnpj=mg cos & sin φ -f У

m («Г + ^ν,Λ^} ~ ^Vl(i) ^{= т}У ^cos ^ ^{cos ψ} + ^z

^Α%-Ε%-ψΒ + qrC - qpE=L ⁽~^}

В - prC -f p-E + rpA - r-E=M’

^Ct~ ^E t -+ 4>E+pqB=N

Здесь X, У, Z выражают собой только аэродинамические силы, которые действуют на летящий аэроплан.

Интегрирование данных выше дифференциальных ур-ий в общем случае представляет непреодолимые трудности, но и в частных случаях нахождение аналитич. выражения движения не всегда представляется возможным вследствие неимения аналитич. выражения действующих на аэроплан сил. Поэтому обычно возможно применять лишь метод последовательного приближения и решения в числах. Однако, во многих интересных случаях даже и это невозможно, т. к. не получено еще соответствующее выражение сил экспериментальным путем.

Прямолинейный установившийся полет аэроплана. При горизонтальном прямолинейном движении все угловые скорости, а также углы тангажа и крена & и φ обращаются в нуль; из внешних сил остаются только силы сопротивления, сила тяжести и сила тяги винта (Ф); т. о., ур-ия (2) в нашем случае получат вид:

C_agSv- - Ф=0, (3)

CyoSv-=тд. (4

Это—основные ур-ия аэродинамическ. расчета аэроплана. Сопротивление аэроплана в зависимости от скорости выражается кривой Пэно, которая имеет для скорости некоторый минимум; эта наименып. скорость полета аэроплана обычно называется посадочной скоростью, так как обычно на этой скорости или близкой к ней самолет приземляется;угол атаки, соответствующий этой скорости, также называется посадочным (или критическим) углом (гпос.-фигура 4). На кривой коэфф-та подъемной силы этот угол атаки соответствует максим, значению этого коэфф-та. Вблизи посадочн. угла в сторону увлнчения углов нарушается

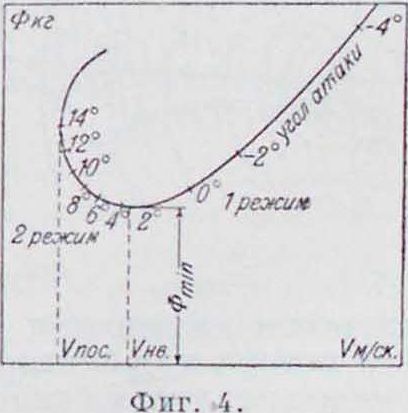
прямолинейная зависимость коэфф. подъемной силы от угла атаки, вследствие наступления «срыва струй», и кривая, переходя через максимум, начинает снижаться. Посадочная скорость м. б. определена из ф-лы (4):

^{υ =} ]/~, где С_у соответствует максималь ному его значению. Если угол атаки больше критического, сопротивление аэроплана возрастает, причем для горизонтального полета требуются бблылие скорости. Режим полета, начиная с угла, соответствующего наименьшейтяге (Ф.нин.) к большим углам атаки, называется в т о-р ы м р е ж и м о м, в отличие от первого ре-ж и м а на углах меньших (фигура 4). На втором режиме полет затруднен, т. к., вследствие малых скоростей, управляемость аэроплана незначительна, и он может сорваться с установившегося движения. Лётным режимом является, главным образом, первый режим. О горизонтальных скоростях по высотам и относительно обозначений—см. Аэродинамика, расчет самолета.

Полет по прямолинейной наклонной траектории. В этом случае, полагая все угловые скорости и угол крена равными нулю, получим основные уравнения следующего вида:

(5)

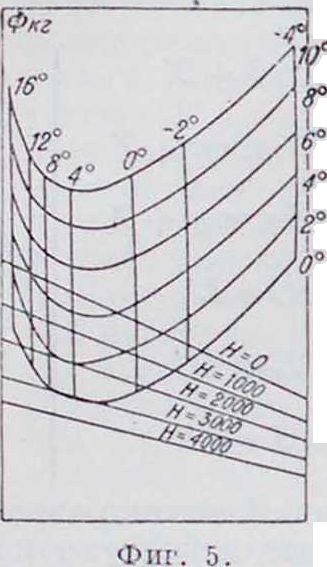
X=mg sin 9, или mg sin &=C_agSv- — Ф Zj — — mg ccs 9, или mg cos 9=C,/j$v-B последнем случае знак изменился потому, что подъемная сила аэроплана направлена вверх, то есть противоположно положительному направлению оси Z. Как и в случае горизонтального полета, можно построить значения величин C„o.Sv² в зависимости от скорости по параметру 9; тогда получим ряд кривых Пэно для подъема или спуска аэроплана в зависимости от величины 9 (фигура 5).

Наклонные прямолинейные траектории полета называются глиссадами. Если будем для данной высоты полета откла дывать радиусы-векторы, дающие^величнну

скорости полета при определенной мощности мотора и ориентированные под соответственными,углами тангажа 9, то концы этих радиусов-векторов в зависимости от 9 опишут некоторую кривую, которая называется указатель и идей глиссад.

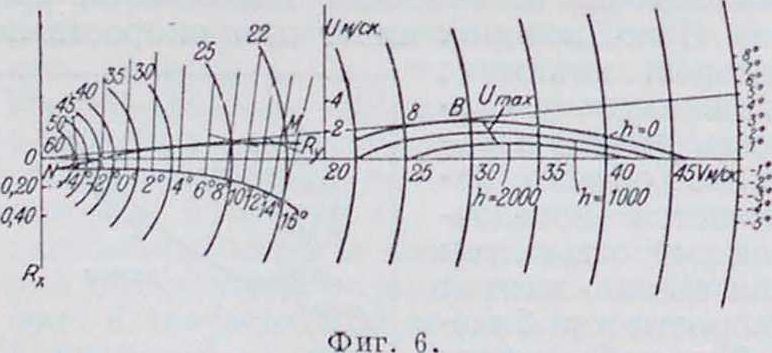
Построение укаэательиицы глиссад делается следующим образом. Строится кривая Лилиенталя всего азроплана в координатах C_uq S**n, и C_TeS= R_c, причем ось подъемных сил направляется гори зонтально. Из точек, соответствующих определенным углам атаки, проводятся линии направлений силы тяги, причем принимается во внимание также наклон оси винта к хорде крыла, от которой отсчитываются углы атаки (фигура G). Из начала координат О в том же масштабе проводятся дуги окружностей ра-G

днусами j, соответствующие различным скоростям о полета. Па линиях тяги винта, заключающих между собой одну из окружностей соответствующих скоро-

Ф

стей, откладывается значение ·, которое находится по характеристике винтомоторной группы для соответствующей скорости. Концы этих векторов соединяются кривой—эквидистантной кривой Лилиенталя. Пересечение полученной кривой с соответствующей окружностью даст точку, а после такого построения для всей кривой Лилиенталя получится кривая MN. Па продолжении оси ΟΙϊ_ν проводят в каком-либо масштабе окружности, соответствующие тем скоростям

полета, для которых отроилась кривая ΜΝ. Из центра О через какую-либо точку кривой ΜΝ проводят прямую. соответствующую определенной скорости, до пересечения с окружностью той же скорости и получают точку, соответствующую вектору скорости но траектории данного самолета. Коли произвести такое построение по всей кривой ΜΝ, то концы получен, векторов опишут искомую указателышцу глиссад.

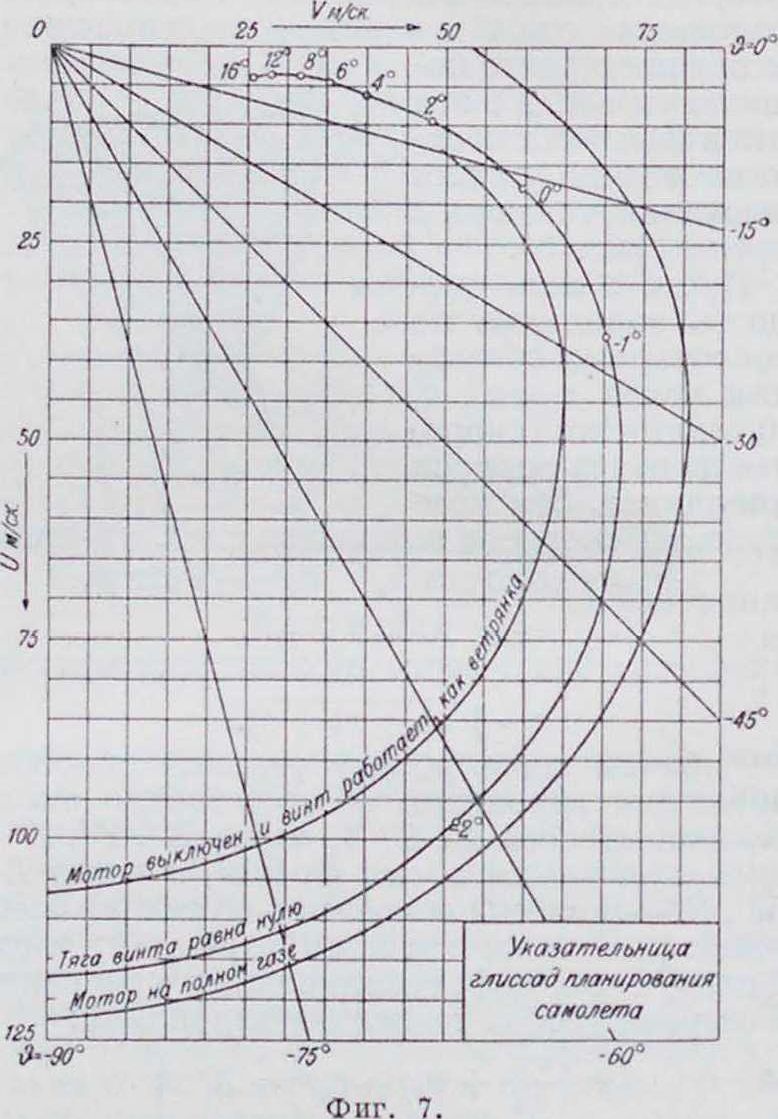
Из указателышцы глиссад видно, что скорости, при которых получается максимальный угол подъема самолета, меньше тех, при которых получается наибольшая вертикальная скорость. В тех случаях, когда снижение аэроплана происходит за счет силы тяжести, то есть без мотора, полет называется планированием. В этом случае Ф =0 и ур-ия движения (2) примут вид: mg sin 9=С_а в Sv‘,

m g cos 9= С_у q Sv²

Для планирования можно также очень просто построить указателышцу глиссад непосредственно из кривой Лилиенталя. Пренебрегая углом атаки а, примем угол планирования 9 равным углу между направлением равнодействующей и подъемной силой,

а на поляре—углу между С_а и С_у (смотрите Аэродинамика). Проводя из начала координат векторы, соответствующие значениям ф-лы

Υ

1

С„е под соответственными углами &, и соединяя концы векторов кривой, получают кривую указателышцы глиссад планирования. При угле планирования 90° планирование переходит в пикирование. На фигуре 7 приведены указателышцы глиссад, которые построены для снижающихся прямолинейных траекторий самолета для трех случаев: 1) тяга винта равна 0; 2) мотор работает на ноли, газе и 3) мотор выключен, и винт работает как ветрянка. В последнем случае скорости полета оказываются наименьшими, т. к. при работе винта как ветрянки получается большое лобовое сопротивление, почти равное сопротивлению диска одинакового диаметра с винтом и выражающееся следующей формулой:

Схв. — Ср g и,

(У)

где Схв.—коэффициент сопротивления винта, отнесенный к площади крыльев, С_р— коэффициент отрицательной тяги винта, F= =0,785 (D² — (ί²)—ометаемая винтом площадь, D—диаметр винта, d—диам. втулки или закрытой коком части винта, S—площадь крыльев, а=~ ^Ьц^1>:—средняя относительная ширина лопасти, z—число лопастей, b_ср.—средняя ширина лопасти, вычисляемая по ф-ле:

Ь_ср. —

развернутая поверхность лопасти пинта радиус

0,40 СР
015
				О

Фигура 8.

На основании данных опыта (фигура 8) можно приближенно принять коэфф. отрицательной тяги Ср постоянным на режимах винта λ > 5; он изменяется лишь линейно в зависимости от относительного шага винта h (см.Воздушный винт). При тяге винта, равной 0, и при моторе, работающем на полном газе, разница в скоростях получается сравнительно небольшая, уменьшаясь с увеличением угла наклона траектории.

Надо упомянуть еще об одном прямолинейном установившемся движении—снижении аэроплана со скольжением на крыло. В практике полетов очень часто скольжением на крыло пользуются в том случае, когда на сравнительно небольшой высоте надо быстро потерять высоту, например при посадке на аэродром малого размера. При скольжении на крыло самолет идет обычно с мотором на малом газе (винт почти но тянет), планируя с некоторым углом крена и рысканья. Вследствие того, что при косом направлении полета получается, с одной стороны, увеличение лобового сопротивления за счет эффекта фюзеляжа, а с другой стороны—уменьшение подъемной силы за счет косой обдувки крыла, получаются условия, благоприятные для снижения при посадке (быстрая потеря высоты без большого увеличения скорости).

Неустановившийся и криволинейный полет аэроплана. Д в и ж е и и е аэроплана вблизи з е м л и (взлет и посадка). Взлет аэроплана можно рассматривать как движение, состоящее из двух частей: во-первых, прямолинейного, неустановившегося движения по земле и, во-вторых, отрыва в воздух. Пас интересует, главн. образом, первая часть этого движения (до момента отрыва в воздух), которую мы и рассмотрим. Движение самолета по земле до взлета необходимо рассматривать как движение горизонтальное и прямолинейное; уравнения его будут иметь вид:

dv_{x v}

т _d?=X,

mg=— Z.

Второе из указанных уравнений существенного значения не имеет, и потому можно ограничиться лишь рассмотрением первого. Внешние силы X, действующ, на аэроплан, будут: сила тяги винта Ф, лобовое сопротивление всего аэроплана Q и сила трения шасси о землю R. Таким образом, первое уравнение имеет вид:

-Q-R. (8)

Здесь, как и раньше, принято, что угол тангажа & не велик и проекции сил на связанную ось×заменены самими силами. С целью более простого интегрирования этого ур-ия вводят некоторые упрощающие условия, а именно: 1) во время разбега угол атаки самолета остается постоянным; 2) коэфф. трения шасси μ, которым условимся обозначать отношение силы трения шасси к весу самолета, не зависит от скорости движения;

3) силу тяги винта определяют по следующей формуле:

Ф=Ф₀ — ορν², (9)

где Ф₀ есть тяга винта на месте. Предполагая, что момент взлета соответствует приобретению аэропланом скорости v_e, соответствующей наивыгоднейшему подъему, получаем:

(J Г,

т-=Ф

dv_x л

^т ж=^ф°

или

σρυ- — С_а oSv² — μ(β — C oSu²),

dv_x .Vo-hG dt ⁼ & —G~

-Ц + ^СаГ^^Су)

γ₀υ-

(Ю)

где C_0] и Су—коэфф-ты лобового сопротивления и подъемной силы всего аэроплана, соответствующие углу атаки, при котором происходит разбег, а γ=ρρ· Интегрируя, получим окончательное выражение для длины разбега:

G

s —

yS

(_s + c_aj - ,с_л)

In --

1/

(П)

i -

Ί’,-μΰ

t/г где Су₂соответствует наивыгоднейшему подъему. Полученная формула чрезвычайно громоздка для вычисления, и для приближенных расчетов можно ее несколько упростить. Т. к. член под радикалом всегда положителен и невелик, то все выражение можно разложить в ряд, оставив только первый член, и тогда получим:

s

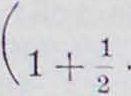
G s+^Cα^^/C"^,

l‘G

"Ух

(12)

Пренебрегая вторым членом выражения, стоящего в скобках, получим следующую приближенную ф-лу:

^S iySCy^-MG) ^

Эта формула во многих случаях практики дает достаточно удовлетворительные результаты.

При расчете разбега гидросамолетов роль трения играет гидродинамич. сопротивление лодки или поплавка, но т. к. кривая водяного сопротивления гидросамолетов в функции скорости не выражается аналитически, а дается обычно в виде эм-пирическ. кривой, то интегрирование пред-взлетного пробега гидросамолета приходится делать графически. На фигуре 9 изображены кривые водян. сопротивления W, воздушного сопротивления Q и тяги винта Ф, причем ординаты, выражающие воздушное сопротивление, отложены от кривой тяги вниз; ординаты заштрихованной площади представляют для соответ ствующих скоростей силы, сообщающие гидросамолету ускорение. Если и—скорость гидросамолета в какой-нибудь момент пред-взлетного пробега, то элемент пути ds=vdt, а весь пробег выразится интегралом

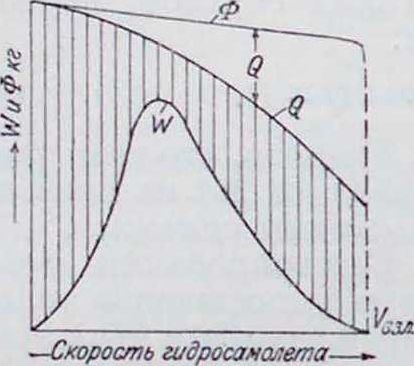
Фигура 9.

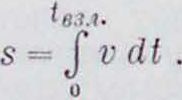
(14)

Если обозначим через j ускорение гидро-^. dv

самолета во время разосга, то есть ) —, то время разбега найдется отсюда как ®«м.

Т= ¹ dv. (15)

О ^J

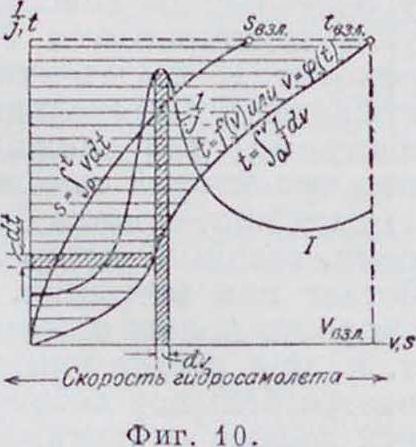
Необходимые графические построения для нахождения интегралов (14) и (15) даны на фигура 10. Сначала строим кривую в функции от V (I); затем обычным образом стро-

V

им интегральную кривую t=f(v)= J. dv.

Ο

Значение ординаты этой кривой, соответствующее взлётной скорости VejA., и будет представлять время разбега гидросамолета. Кривую t =/(а) можно также рассматривать, как кривую «=<?(<), приняв за независимое переменное координату С Площадь, ограниченная этой кривой,абсциссой, соответствующей t=ί_β3Λ, и осью ординат (заштрихованная

Сипа фигура), представляет собою s=Jvdt. Опре делив эту площадь, мы получим, следовательно, длину s предвзлётного пробега. Путем последовательного интегрирования мож-

(

но построить также кривую s — f v dt.

О

Все вышеописанные ф-лы были выведены в предположении, что аэроплан взлетает при безветрии; нетрудно вывести формулы для соответствующих элементов, предполагая, что ветер дует со скоростью w, так как скорость ветра является переносной скоростью. Аналогично разбегу аэроплана, можно получить и уравнение движения его при пробеге после посадки. В данном случае, полагая в уравнении (10) Ф₀~0 и σ=0, получим уравнение вида:

— у (16)

Обычно при посадке самолет, подходя к земле, понемногу теряет свою горизонтальную скорость и садится или па скорости больше посадочной, соответствующей углу атаки наибольшей подъемной силы, или равной ей; однако, бывают случаи, когда летчик слишком рано выравнял самолет (то есть перевел траекторию его полета у земли из наклонной в горизонтальную) или самолет, ударившись колесами об землю, отскочил от нее,теряя горизонтальную скорость. В обоих случаях может произойти след, явление: самолет, потеряв свою горизонт, скорость до посадочной, продолжает ее терять, причем, вследствие уменьшения подъемн. силы, он начнет приобретать вертикальную скорость и с силой ударится о землю. Это явление — потеря скорости за границей посадочной и снижение на углах выше критического — называется парашютиро ва-н и е м аэроплана. Для составления дифференциальных ур-нй парашютирования можно ввести следующие условия: 1) самолет при парашютировании остается параллельным самому себе; 2) коэфф. сопротивления аэроплана остается постоянным. Уравнения движения примут вид:

т=— mg sin 0 + X,

т ⁽ⁱj₍-=mg cos & -f Z.

Т. к. эти ур-ия не интегрируются в простых ф-иях, то выберем другую систему координат ξ, г/, ζ. Пусть ось Од будет направлена но линии равнодействующей воздушных сил, а ось Οξ ей перпендикулярна (фигура 11); тогда получаются следующие дифференциальные уравнения: d²(.

_αγ,=~ 9 sin г

Разделив второе ур-ие на первое, получим:

(17)

*».=_ cto· i 4- - ¹

di ^{1 i} vi

5 sin i cos

пК^ + ч“]. (^1S)

Введем новые переменные т и (

£== - ί>ο V sin г cos г т

V -=«о l⁷sin i cos i ζ

В начальный момент парашютирования, то есть когда самолет летит еще горизонтально на посадочной скорости, будем иметь ίό= v₀ cos г, η₀=t’o sini ; подставляя эти значения в уравнение (19), получим:

т₀=— Vctg г; С₀= j/tgi.

На основании уравнений (19) уравнение (18) Приводится к виду:

+ £² + т²=ctg г. (20)

Это ур-ие есть ур-ие тина Риккатп; проинтегрировать его можно одним из способов приближенного интегрирования. Так как при посадке самолета почти всегда бывает небольшое парашютирование, то теория

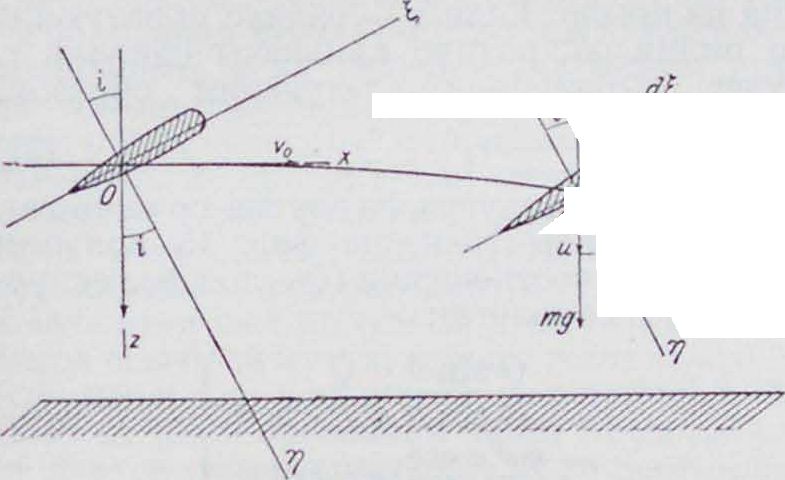
Фигура 11.

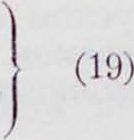
парашютирования чрезвычайно важна для расчетов амортизаторов шасси. Парашютирование самолета можно рассматривать как фиктивное падение тела той же массы в пустоте, причем вертикальная скорость выразится: «=VZgz, где z—высота падения в пустоте; при этом часть живой силы самолета поглощается ударом шасси и растяжением амортизатора. Часть веса самолета приходится на долго крыльев, обозначим эту долю (1 — i)G, причем ξ примерно имеет

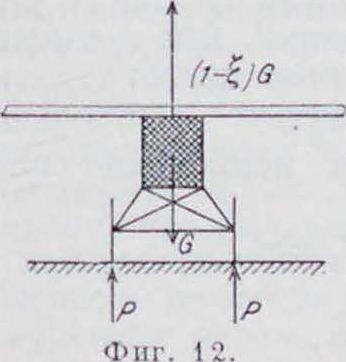
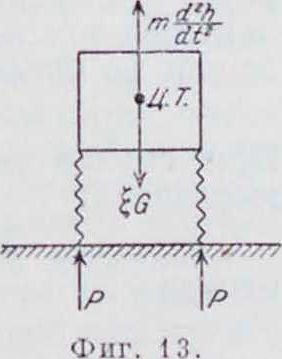
значение от 0,2 до 0,3 (фигура 12). Т. о., движение самолета после касания земли сводится к тому, что самолет весом ξΟ падает с некоторой высоты Н на землю. Обозначив через h перемещение ц. т. самолета при посадке за счет деформации амортизаторов (шины, амортизационный шнур, прогиб оси и т. и.), получим следующее дифференциальное ур-ие движения ц. т. (фигура 13):

т 2 + 2 Р - HG, (21)

где Р—сила упругости каждой стороны шас си, зависящая от h, причем эту зависимость можно принять линейной, то есть Р - Eh (Е можно принять равным 170 килограмм;см). Подставляя это выражение в уравнение (21), получим:

££ + <«%-&. (22)

Здесь

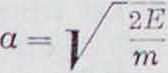
Общий интеграл ур-пя (22) будет: h —A sin (at- β) + -₂g

По начальным условиям в момент I —0, имеем h=0, jij — u · Отсюда

tQ

a A cos β=и₀; A sin β=_2/, ·

Решая эти уравнения, получим:

л _ _{= Ί} ^(;" 7

^Л У 2 Е ¹ 4 Е^г у Е ⁺ arc tg(;|/_if_H)·

_£-Q2

4E- ’

Таким образом, движение ц. т. аэроплана приводится к гармоническому колебательному движению с периодом

а

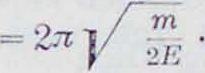
(23)

Максимальная величина хода ц. т. будет:

h =* — + 4.=^SG

"max 2E *

(24)

Отношение максимальной получившейся нагрузки к общему весу, то есть так называемая перегрузка шасси п, выразится:

2 Р„

п =

,-$+> Ρ + ψ- (25)

Наиболее сложны.ми движениями аэроплана являются криволинейные движения как установившиеся, так и неустановнвшие-ся. К таким полетам относятся т. н. фигурные полеты (смотрите). К установившимся криволинейным полетам можно отнести вираж и спираль; к неустановившимся движениям относятся мертвая петля и штопор, хотя последний в некоторых случаях можно рассматривать и как установившийся полет. Но всех неустановившпхся полетах, а также и при криволинейных полетах подъемная сила аэроплана не равна соответствующей составляющей веса; в этом случае отношение подъемной силы к весу будет называться перегрузкой самолет а. Как мы выше видели, при прямолинейном полете подъемная сила всегда равна составляющей веса, и поэтому перегрузки быть никогда не может. Перегрузка может получиться или при быстрой перемене угла атаки, так что скорость не успеет еще измениться, или когда имеется постоянная инерционная сила (наир., центробежная). Перегрузка тем больше, чем быстрее происходит перемена положения самолета и чем больше разница в начальном и конечном угле атаки. Т. о., наибольшая перегрузка получается при выходе из пикирования, и чем резче выход, тем больше перегрузка. Положим, что самолет пикирует со скоростью υ и летчик, быстро действуя рулями, переводит самолет сразу на прямолинейный полет на критическом" угле атаки; тогда подъемн. сила сразу

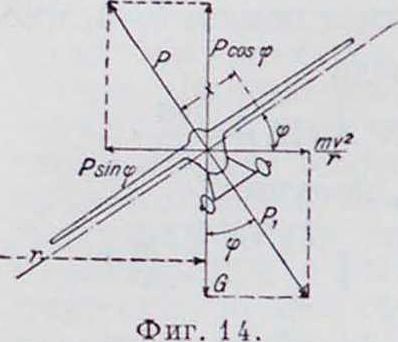
от 0 достигает величины С nSv², где С„

_ Ут »т наибольшее значение С„: для горизонтального полета на том же угле атаки подъемная сила будет C„_mgSvl, следовательно, перегрузка в данном случае будет:. Пере грузки играют чрезвычайно важную роль в расчете самолета на прочность.

Интегрирование дифференциальных ур-ий криволинейных полетов аэроплана представляет большие трудности и обычно не м. б. доведено до конца; поэтому теоретически приходится решать задачи или приближенно или, чаще всего, в числах для данного примера, рассматривая движение от одного положения к другому. Значения перегрузок, необходимых для составления норм прочности, чаще приходится искать экспериментальным путем, т. к. в этом случае учитываются все случайные причины, вызвавшие ту или иную перегрузку. Запись перегрузок на самолете производится так называемым перегрузочным прибором (смотрите).

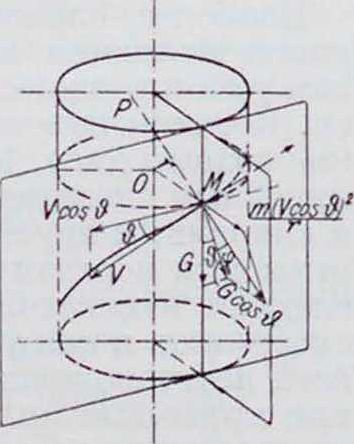
Вираж. При вираже на аэроплан действуют следующие силы: 1) подъемная сила крыльев, 2) вес самолета, 8) центробежная сила, 4) лобовое сопротивление самолета, 5) тяга винта. Вираж называется нормальным в том случае, когда равнодействующая центробежной силы и веса самолета прямо противоположна подъемной силе крыльев; в противном случае получается нек-рое скольжение на крыло. Т. о., виражем называется установившийся полет "по круговой горизонтальной траектории; если траектория наклонна, то вираж переходит в спираль. На фигуре 14 дано расположение сил в плоскости, перпендикулярной продольной оси самолета. Подъемная сила, то есть сила, перпендикулярная направлению движения и плоскости, проходящей через поперечную и продольную ось самолета, будет выражаться: p=c_veSv“. (26)

Согласно фигура 14, будем иметь следующие выражения:

Р cos ψ=G;

Р sin φ=^mv

^Г Г

Перегрузка при вираже выразится:

^п-^Рα= ШГ„- (²⁷>

8. о., перегрузка зависит от угла крена: чем больше крен, тем больше перегрузка.

Из фигура 14 молено найти и радиус виража. Действительно, имеем:

Фигура 15.

mv¹

~гГ~ tglp.

(28)

Если обозначим через v₀ скорость прямоли нейного горизонтального полета под тем же углом атаки, какой имеется в рассматриваемом вираже, то для горизонтального прямолинейного полета будем иметь:

G=C_vq Sv%.

Принимая во внимание формулу (20), получим:

или

-г=П,

V=V₀ У п.

(29)

Подставляя в формулу (28) т=® и скорость из формулы (29), получим значение для радиуса виража:

т — · (зо)

Спираль. Движение аэроплана по спирали есть такое движение, при к-ром ц. т. его описывает спиральную линию. Спираль называется правильной, как и в случае виража, когда она производится без скольжения накрыло. Если г—радиус образующего цилиндра, радиус кривизны спирали г₀будет выражаться следующим образом:

b-Ш··- (31)

В случае планирующего спуска по спирали, то есть без силы тяги, из фигура 15 получим следующие соотношения (Q—лобовое сопротивление самолета):

G sin &=Q i G cos К=Р cos ψ I, (32)

mv* cos¹ 0 ·»-.

— -=P Sin φ I

Деля первое уравнение на второе, найдем угол снижения:

tg & =

P cos φ

ИЛИ t£ ft =

μ

COS ν ⁹

(33)

c„

где P p c_y

Перегрузка самолета на спирали найдется из второго уравнения (32):

Р COS 0

G cos ψ

Если обозначим, как и выше, через ν₀ скорость прямолинейного горизонтального полета под тем же углом атаки, как и в движении по спирали, то будем иметь:

G=C,QSvi.

При спуске по спирали подъемная сила выразится:

Р=Gn=C>.SV,

откуда

ν — ν₀ У η.

Подставляя выражение Р в третье из уравнений (32), получим выражение для радиуса образующего цилиндра ОМ:

_ G cos’ О ~ gCydS sin φ ’

или, принимая во внимание ур-ие (33),

_r=£._J___<»<>-»__сз4

g CyeS sin φ (cos* φ + μ’)

Снижение за один оборот по спирали будет равно:

h=2лг tg 9,

или, вставляя сюда значение г из уравие-

ння (34) и угол & из ур-ия (33), получим:

, 2лG /I ctg φ ~ (iCyeS COS’ φ +μ¹

Угловая скорость вращения самолета по образующему цилиндру будет:

V cos о со =

г

Мертвая петля. Правильн. мертвая петля должна производиться в одной вертикальной плоскости без какого бы то ни было скольжения на крыло; поэтому в данном случае общие дифференциальные уравнения движения, принимая *’.,=0, j>=0, г =0, φ=0, У= 0, L= 0, Ν— 0, будут:

+ ОД=- 9 sin ^& + X

!,’г - ^ГЛ=0 cos & + Z (35)

^rtq. 13= M i

at

Здесь X, Z и М—силы и момент, вызванные только воздушным сопротивлением. Интегрирование этих ур-ий не представляется возможным, и их решение мы можем найти только приближенно, делая определенные предположения и производя последовательно построения для положения аэроплана от одной точки к другой. Воздушные силы могут быть найдены исследованием в аэродинамич. лаборатории, причем компоненты этих сил по оси×и по оси Ζ находятся обычным путем, момент же тангажа М находится для различных отклонений руля высоты. Если обозначим через I расстояние от центра тяжести аэроплана до центра давления горизонтального оперения и через М_с момент горизонтального оперения, то уравнения (35) примут вид:

^d”*---v.q - g sin & +

CiqSv’, m

Φ

ϊ

τη

^dll ^{= ν}Λ + 9 cos о +

Саазу, m

Μη

ml

я,

dq _ Μ dl~ b

M_r

В

• Я

(обозначения C_t и С„ см. Аэродинамика). Построение траектории мертвой петли м. б. сделано при различных предположениях, как то: выдерживание постоянной перегрузки, выдерживание постоянного угла атаки, выдерживание постоянного угла руля высоты и т. и. Вычисления траектории мертвой петли и всех сопутствующих ей элементов движения для отдельных аэропланов показали, что они сходятся довольно близко с наблюденными на практике величинами. Скорость на петле уменьшается до наивысшей точки петли, после которой она снова увеличивается; углы атаки вначале быстро увеличиваются, потом остаются нек-рое время постоянными почти до вершины петли, к самой вершине опять уменьшаются. На фиг, 16 дана примерная траектория петли. Перегрузки, получаемые на петле, зависят от радиуса кривизны петли, то есть от той резкости, с которой эта петля производится. Истребители с большим запасом мощности, делающие петли со сравнительно малым радиусом, получают ббльшие перегрузки, чем более тяжелые машины. На фигуре 16 указаны как величины перегрузок п, вычи сленных теоретически, так и углы атаки а и скорости V. Опытные исследования показали, что обычная мертвая петля, сделанная не особенно резко, дает наибольшую перегрузку порядка 3; при узких же петлях перегрузка может дойти до 6.

Штопор. Штопор является одной из фигур полета аэроплана, динамика которой наименее выяснена. Он характеризуется тем, что аэроплан снижается по очень крутой спиральной траектории; таге, образом, штопор можно рассматривать как спираль с очень большим наклоном; ц. т. аэроплана в этом случае описывает винтовую линию со сравнительно малым радиусом (часто меньшим размаха крыла) образующего цилиндра. Харак-торн. особенностью штопора является то, что углы атаки, на которых происходит движение, значительно выше критического. Т. к. аэродинамические силы на таких углах атаки, вследствие срывов струй, не носят закономерного характера, то это уже одно вносит значительные затруднения в исследование штопора. Рассматривая штопор как спираль, мы получим для него следующие элементы:

V cos &

угловая скорость ω=* ——;

2-т время одного витка t=- ;

снижение за один виток h =2яг tg &=v-1 sin о;

P cos &

перегрузка n= G=_cos9> ·

Вследствие несимметричности движения аэроплана в штопоре, моменты, заставляющие аэроплан вращаться, получаются от действия воздушного потока почти на все главнейшие элементы аэроплана. Т. о. получаются моменты крыльев, моменты оперения, моменты фюзеляжа; кроме того, действуют еще и моменты от инерционных сил. Главнейшее действие оказывают моменты крыльев. При штопоре мы сталкиваемся с явлением г. н. авторотации, которая состоит в том, что симметричная поверхность в установившемся потоке под влиянием первоначального импульса входит в установившееся вращательное движение. Авторотация крыльев происходит за счет получающегося несимметричного обтекания крыла потоком. Найти эти моменты теоретически можно лишь приблизительно, суммируя действия отдельных элементов, то есть предполагая независимость действия отдельных элементов друг на друга. Для каждого такого элемента его характеристику приходится брать из испытаний крыла в нормальных условиях (смотрите Индуктивное сопротивление). На авторотацию крыльев влияют как геометрическая форма крыльев, так и относительная скорость потока и угол атаки. Как показывают расчеты, с увеличением угла атаки увеличивается и угловая скорость

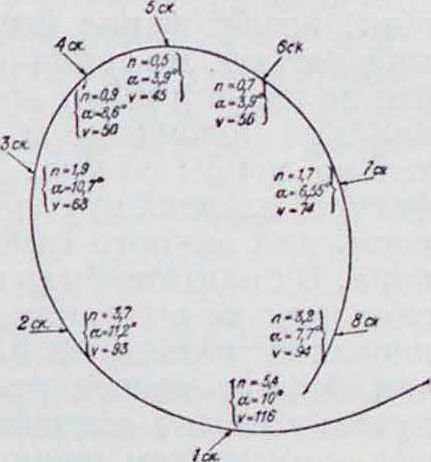
Фнг. 16.

вращения, причем наиболее интенсивное вращение получается на углах атаки выше критического. С увеличением скорости потока также увеличивается угловая скорость вращения. С другой стороны, при увеличении относительного удлинения крыла уменьшается угловая скорость вращения.

Вследствие взаимного влияния различных частей самолета друг на друга, точного решения задачи о штопоре до сих пор получить не удалось. Необходимы как нек-рые специальные аэродинамич. исследования над моделями в аэродинамич. трубе, так и, гл. обр., исследование штопора над самолетами в натуру. До сих пор удалось установить, что на штопор имеет довольно значительное влияние положение ц. т. самолета относительно хорды крыла. Практически в этой фигуре главнейшую роль играет возможность для данного самолета выйти из штопора. В практике было много случаев, когда самолеты не выходили из штопора и полет кончался катастрофой. Оказывается, что, чем больше вперед расположен ц. т., тем лучше выходит самолет из штопора; наоборот—при заднем расположении ц. т. самолет выходит из штопора вяло или даже может совсем из него не выйти.

Эксперименты, произведенные в полете, дают наибольшие значения перегрузок от 2 до 4. Английские наблюдения над самолетом FE 2В дали следующие характеристики индивидуального штопора:

Наклон траектории..в=S0°

Угол крена..φ=7S⁰

Угол атаки..α= 35“

Радиус витка..г=2,4 ,н

Лит.: Ветчин к и н В. П., К а м е и е в С. и. и Ченцов II. Г. Динамика полетов, М., 1926; Горяйнов Л. и Кузь м и н Г. Нормы прочности самолетов при статическ. испытаниях, М., 1926; II ы ш н о в В. С. Самовращепие и штопор самолетов. «Техника воздушп. флота». Л., 1927, 2; его же. Свойства вращающихся крыльев, там же. 1928, 3; Ухов Б. С., Расчет предвзлбтного разбега гидросамолета, там же. 1928, 5 : В a i rs tow L., Applied Aerodynamics, L. 1920: Devi 1 lers R. La dynamique cle 1avion, P. 1920; В lent H., Startformeln Г. Landflugzeuge, «Jahrb. d. Deutsclien Versuchsanstalt f. Luftfahrt». Mch.—B., 1 927; L a n d e m a n n. G 1 a u-o r t a. Harris, The Experimental a. Mathematical Investigation of Spinning, «Technical Reports of tlie Aeronautics Advisory Committee», London. 1921. 411; Г. 1 a u c r t, Investigation of the Spin of an Aeroplane, ibid., 1923. CIS; (I a t cs and В г у a n t, The Spinning of Aeroplanes, ibidem. 1927, 1001; Bryant a. G a t e s, The Spinning of Aeroplanes, «The Journal or the Royal Aeronautical Society», London, 1927. 199. В. Александров.