 > Техника, страница 43 > Динамика поршневых двигателей
> Техника, страница 43 > Динамика поршневых двигателей
Динамика поршневых двигателей
Динамика поршневых двигателей занимается изучением динамических усилий, возникающих в этих двигателях вследствие периодическ. изменения скоростей движения поршня и шатуна (силы инерции), а также вследствие периодичности действия вообще всех сил двигателя (вибрационные явления). Сюда же относятся и вопросы уравновешивания инерционных усилий и выравнивания вращательных моментов поршневых двигателей (смотрите Уравновешивание поршневых двигателей). Поршневые двигатели старых конструкций строились для малого количества оборотов и с малыми скоростями движения поршня. Па влияние сил инерции движущихся частей двигателя обращалось поэтому мало внима ния. Лишь постепенно, с увеличением скоростей поршневых двигателей, сначала в паровых, затем в др. двигателях, конструкторы были вынужде-ны учитывать вли-
янио этих сил инер-. —rg— ~ (&, V.
ции. Радингер впер- -v·. J
вые в 1867 году час- ^
тично обосновал тео- фигура i.
ретически Д. и. д.
Сила инерции поршневых двигателей рассматривается как состоящая из: а) силы инерции поршня и б) силы инерции шатуна.
С н л ы инер ц и и поршня (фигура 1). Обозначим через Мх массу поршня и всех частей, движущихся вместе с ним со скоростью с; через v—окружную скорость пальца кривошипа, 11 —длину кривошипа, L— длину шатуна, а—угол кривошипа, β—угол шатуна. Путь, пройденный поршнем от начального положения:
s=R · (1 — cos а) ± L (1 — cos β).
Здесь знак ( + ) — для движения кривошипа от начального положения А0 и знак ( —)—для движения его от начального положения В0. Из ур-ия движения поршня определим его скорость
(sin n ± sin 2ct).
Λ (Is sin (a -f- β)
C== V · - — v» V
at cos β
Ускорение поршня определится:
dc __ и“ rcos (a ± β) В COS* «Л
P - <n~ it L coiβ i. cos*/U *
Силы инерции поршня будут, т. о., Ру М ,р. Приближенное выражение для этих сил инерции имеет вид:
Pj S Мг · д · (CCS а ± f cos 2a).
Существует ряд способов графнческ. постро ения кривых инерционных усилий поршня, напрнм. способ Холле. Очень удобен способ построения этих кривых (фигура 2) по величинам 11 ординат, равноотстоящих друг
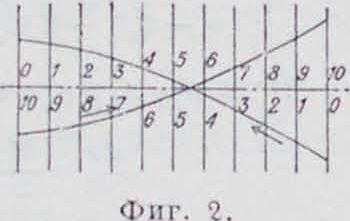
от друга (смотрите табл. 1) для
7?
L
1 Л_1
’ Ь = 6
4
R
L
1
6
Таблица 1.— Вели ч и н ы cos a ± ^ cos 2a.
| Орди ната | R 1 L | R 1 | л 1
L =б" |
Орди ната |
| 0 | 1.250 | 1.200 | 1.167 | 10 |
| 1 | 0.938 | 0,907 | 0.888 | 9 |
| 2 | 0,644 | о.сзо | 0.622 | 8 |
| 3 | 0.368 | 0,369 | 0.371 | 7 |
| 4 | 0.114 | 0.127 | 0,136 | 0 |
| 5 | -0.117 | -0.096 | -0,081 | 5 |
| 6 | -0.321 | -0.296 | -0,279 | 4 |
| 7 | -0.493 | -0.471 | -0.457 | 3 |
| 8 | -0.628 | -0,616 | -0.610 | 2 |
| 9 | -0,717 | - 0.728 | -0.737 | 1 |
| 10 | -0,7.90 | -0,800 | -0,833 | 0 |
Силы инерции шатуна (фигура 3). Движение шатуна можно рассматривать как состоящее из двух движений: поступательного в направлении движения поршня, подчиняющегося законам движения последнего,
и колебательного около споего среднего положения, совпадающего со средней линией
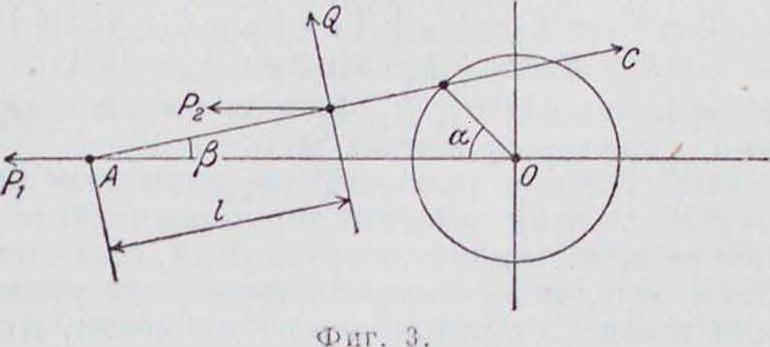
двигателя. Силы инерции Р2 при ноступат. движении шатуна определятся так лее, как и силы инерции поршня, и выразятся так: р - м. *“. r,:os <" £) в со£ i * - i: L @os β L cos J
а М2 (COS α ± f · COS 2а) ;
здесь М.,- -масса шатуна. Колебательные движения шатуна вызывают инерционные усилия двух родов: 1) силы инерции Q качания и 2) центробежные силы С, возникающие при вращении шатуна вокруг мгновенного центра А. Силы Q определяются путем на г dft
хождения скорости качания шатуна L (Пи ускорения этого качания. Для сил инерции
Q=— М2
качания шатуна, приложенных в его ц. т., получим, таким обр., следующее выражение: V2 U - R1 I sin а R L* I. cos*/J Центробелшые силы С шатуна определятся из выражения:
С _ I в cos* а.
° ~ Н 1* cos5 0 ’
здесь !—расстояние центра тяжести шатуна от его малой головки.
Равнодействующие инерционных усилийкривошипного м е х а-н и з м а. Разложив каждую из полученных нами сил инерции Ри Р.г, Q и С на две составляющие, вдоль средней линии АО и перпендикулярно к ней, и суммируя эти составляющие, получим: 1) сумму всех инерционных усилий системы, действующих вдоль средней линии двигателя:
Р=Pj + Р2 + Q · sin β — С ccs β =
= (Μχ + Μ2) lR · ccs a ±
if- (Μ, + M2 Ll ) · |. cos 2a;
2) сумму всех инерционных усилий системы, действующих по направлению, перпендикулярному к АО:
Q ccs β + С sin β=М2 lR sin a. Если из полученной силы Р вычтем силу,
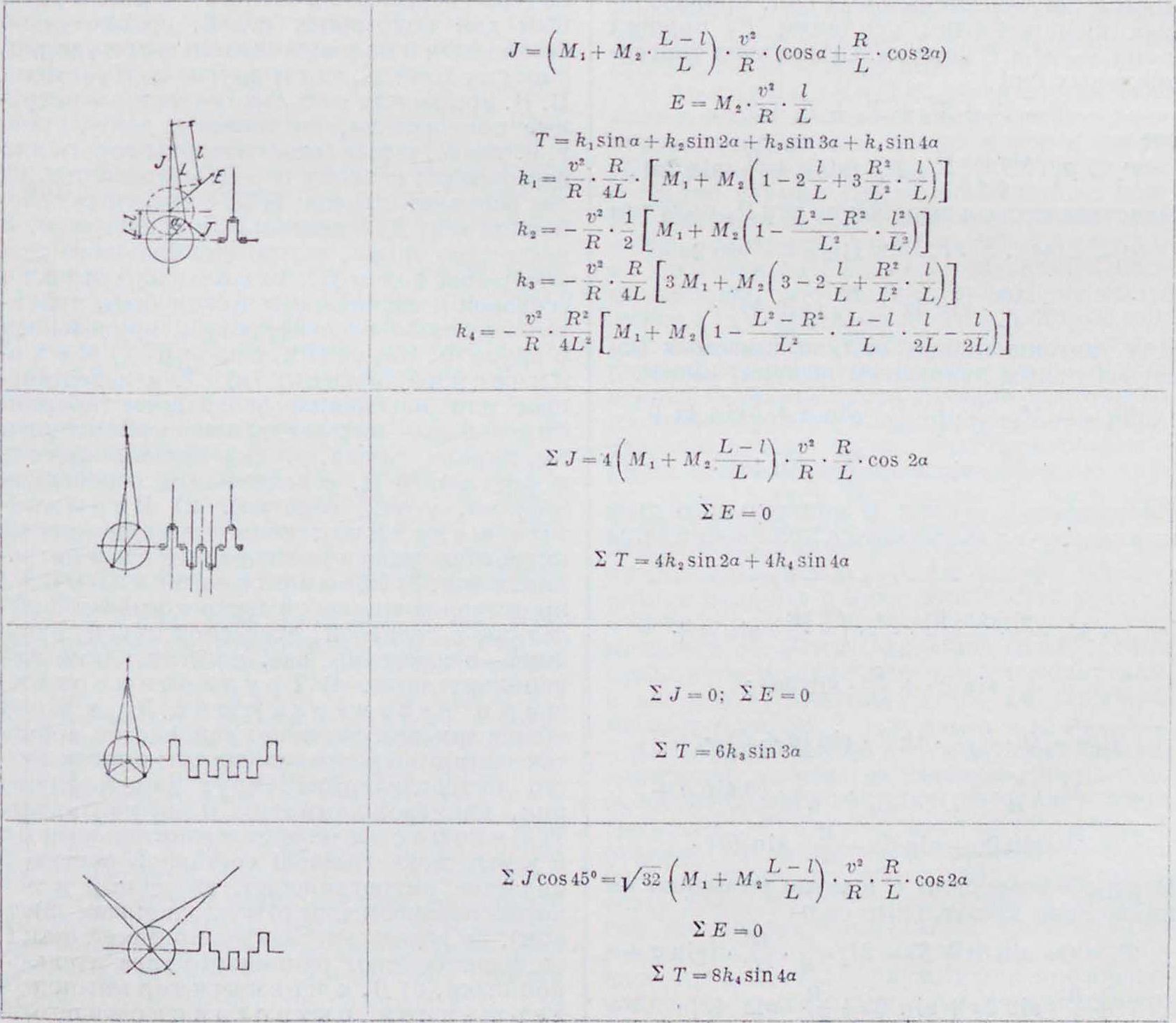
Таблица ".-Формулы для определения равнодействующих инерционных у с и л и й.
, υ*
равную Μ2 · R · cos α, и сложим эту силу с только что полученной перпендикулярной к ней силой М2 · R · sina, то будем иметь в конечном итоге: 1) сумму всех сил инерции, действующих по направлению АО:
J=(Мх+Мг· L~() · R (cos a ± ·*? · cos 2a);
2) равнодействующую сил Мг · · · cos a π
„ »* г
Ма · R L sin a:
T. о., все инерционные усилия системы поршня и шатуна разлагаются на две силы J и Е (фигура 4). Последнюю можно рассматривать как центробежную силу массы М2 }, вращающейся на расстоянии R вокруг центра вращения О со скоростью V. Направление этой силы всегда параллельно кривошипу.
Центр вращения О находится на расстоянии L—1 от центра вращения О кривошипа.
Тангенциальные (касательные к окружности кривошипа) с и л ы и и е р ц и и слагаются из тангенциальных сил, производимых инерционными усилиями Рг поршня и сил Р2, Q и С шатуна. Сумма этих тангенциальных сил г=T1 + Ti+Ti + Ti + Ts, где
Τι - Рг *Рг (sina + 24 sin 2a).
Подставляя сюда выражение дляРцполучим Тι= - Μχ ), · (- 4 · sin a + ‘ sin 2a +
+ 4 · sin 3a + 4·sin 4a) ·
Для тангенциальных сил, вызываемых поступательным движением шатуна, имеем:
Г,- — М2 · ^ sin a -f l sin 2a +
+ J · sin 3a -(- -£j · sin 4aJ ·
Инерционные усилия Q качательного движения шатуна вызывают на кривошипе силы
~ · ccs (a + /?) =
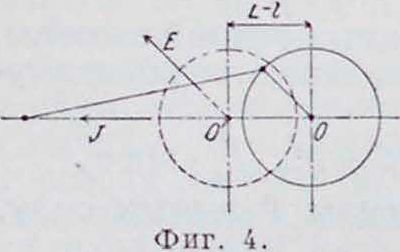
| = мг | г“ | IJ - R* П | 3R |
| R | U L* | (- iL · Sin α + | |
| Л--1 2 | sin 2α + 4 | • sin 3α) ; | |
| 7 =- | Q- | 1τ1·4β· | sin (α + /5) = |
| = - м2 | V*
R |
L-R* 111 L 4L | • L~1 · (3 sin α + |
| +ί- | sin | 2α — sin 3α - | -4« sin4α) |
Центробежные силы С шатуна вызывают на кривошипе касательные силы ть=С sin (a + β)= Μ, · I - 4 (sin a + + £ · sin 2a -f sin 3a+ 4 · sin 4a)
Таким образом, сумма всех тангенциальных сил имеет следующий вид:
Т=T1 + Tt + Ta + Tl + T6=кх · sina-|-+ fcj · sin 2a -f k3 · sin 3a -f kt sin 4a. Коэффициенты /с, k2, k3 и kt имеют значения, указанные в таблице 2.
Определение равнодействующих инерционных усилий многоцилиндровых двигателей не представляет затруднений, если известны отдельные составляющие этих усилий для каждого цилиндра в отдельности. Приведенная табл. 2 дает ф-лы для этих равнодействующих для ряда случаев многоцилиндровых двигателей, у которых массы поршней и шатунов, а также ходы поршней для всех цилиндров одинаковы.
Jlum.: 1’ е л ь д Г. А., Судовые двигатели Дизеля, П., 1922; Л e η е и с о и Л. К., Кинематика механизмов, М., 1923; Д у б 0 е л ь Г., Двигатели внутр. сгорания, Одесса—М., 1927; Radinger L., Uampf-maschinen mit holier Kolbcngeschwindigfeeit, 3 Auf-lage, Wien, 1893; Lorenz H., Dynamik dos Kurbel-getriebes, Lpz. 1901; Hort W., Teclinische Schwin-gungslehre. B., 1922. Л. Мартенс.