> Техника, страница 43 > Диполь электрический

Диполь электрический

Диполь электрический, система, образованная двумя равнопротивоположными электрич. зарядами, находящимися в некотором расстоянии друг от друга. Произведение абсолютной величины зарядов η на вектор /, идущий от отрицательного к положительному заряду, называют электрич. моментом диполя:

М=ql. (1)

Этот момент обычно является периодичсск. функцией времени. Д. является простейшим элементом, рассматриваемым при излучении электромагнитной волны. Для определения излучения обращаемся к ур-иям Максвелла:

«af-rot 11, (I) —=rot JS; (II)

div jE= 0; (III) div if=0; (IV)

В координатах эти ур-пя имеют следующий вид (Н„ совпадающая по направлению с М, равна нулю):

е ОЕ_х дНу с οι ~ Ύ_ζ

^е дИж. /тч с ’ 01 Οζ 1 ’

- _ ΘΕ, ₌ дНу _ ΟΗχ с 31 Ох Оу,

/<	дНх	ПК.	_ а_%
с	Ы	Чу	Οζ
я.	_ $ Ву	ΟΕχ	_ 9KS
с	dt	όζ	Ox

QEy _ οι·:_χдх ду

(П)

выражений (7)—величины разного порядка относительно переменной г. На малых расстояниях все члены ничтожно малы по сравнению с первыми, зависящими от минимальной степени расстояния. Кроме того, при малом г можно считать, что

0Ε_ν -0_Е_? „

OX Oyuz

Oilх, ОНу „

дх 6 у

Здесь ί—диэлектрический коэфф. среды, μ— проницаемость, с—скорость света в пустоте. Как показал Герц, эти ур-ия можно интегрировать при помощи вектора Герца 7“, удовлетворяющего дифференциальному ур-ию:

(ИГ)

(IV)

или в координатах:

с“ 01* ^— дх“

Тогда где

cVII _ 041 041, 041

„h — я,.! + 0yi +

|/ε E=rot rot J

Υμΐι-ί -^rot 7>,

V =

(2)

гЗ)

(4)

(δ)

скорость распространения света в данной среде. Гели электромагнитное иоле создается Д., заряд которого колеблется по какому-либо закону, то вектор Герца будет иметь постоянное направление, параллельное оси момента Д. Модуль этого вектора П м. б. выражен в этом случае при помощи ф-лы

/(«- I)

П- г (6)

в которой /—произвольная функция, непрерывная вместе с первыми двумя производными по координатам и по времени, а г—расстояние от центра диполя. Получаемый таким образом интеграл дает сферическую волну, распространяющуюся из начала координат со скоростью V.

Вид функции очевидно будет определяться характером движения зарядов в колеблющемся Д. Временно оставляя вид функции неопределенным, находят составляющие магнитного и электрич. векторов. Если момент Д. параллелен OZ, то уравнения (3), (4) и (G) дают для проекций Е и Л выражения:

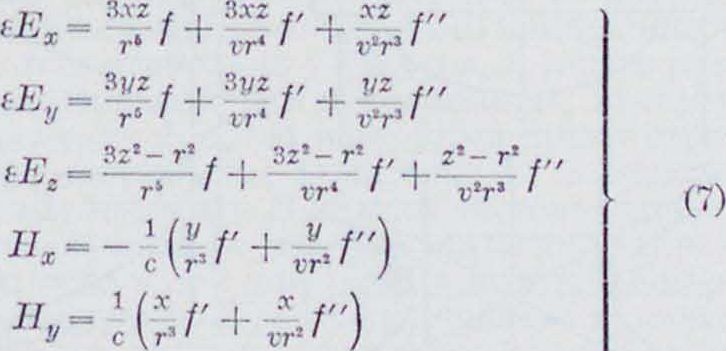
Н_г= О

Выражения (7), так лее как и (6), обращаются в бесконечность в начало координат. Следовательно, найденные решения не дают физически верной картины поля в непосредственной бЛИЗОСТИ 1C Д.

Выделив эту часть, рассмотрим ур-ия (7) во всем остальном пространстве. Слагаемые

(8)

В виду этого в части, близкой к Д., ур-ия (7) принимают такой вид:

ai

я,-о )

Чтобы определить вид функции /, сравним электрическ. поле, определяемое выражениями (7), со статич. полем Д. Это сравнение приводит к необходимости выбрать ф-ию таким обр., чтобы вблизи начала координат она переходила в переменный момент Д.:

/(<-;)=м(«--д. о)

Рассмотрим теперь поле вдали от Д. в волновой зоне (смотрите). При достаточно большом г, в выражениях (7) молено пренебречь всеми членами за исключением последних, содержащих г в максимальной степени. Введем сферич. координаты:

*=sin ficos <Р, ^vr=sin fl sin φ, *=cos О, (10)

где fl—зенитное расстояние, а у—долгота сферической системы координат; тогда

bE*=³*f/(0 iE_y^m

τη 32^е—Г* ,_1Ч

з /(f)

fEj.= — у) cos φ sin fl cos &

tE_y= _v!_r/"(f — ^ sin φ sin &cos fl eE,=—L/"(f —sin’ fl ^нX=- ^ /" (l - ") sin <P sin fl 11 _υ=— /" (i — ^r) cos φ sin fl

и,- 0

Из этих ф-л видно, что Е и 11 совпадают по фазе. Обычным образом можно найти, что

E ± h, E i г и Л ± г. (11)

Следовательно, в волновой зоне, на поверхности сферич. волны, линии магнитного поля совпадают с параллелями, а линии электрического поля—с меридианами. Абсолютная величина векторов Е и Л определяется уравнениями:

Е - ] к и i К+Щ+ΈΙ ,!._rr(f

Из ур-ия (12) видно, что вектор nofiimiiiraS (плотности энергии) направлен по радиусу сферы; по абсолютной величине он равен:

8 ~^ Е - Н --^П(*-^·». (13)

Энергия, которая излучается колеблющимся диполем за время ί, определяется как поток вектора энергии через всю поверхность сферы за время I:

2 я л I

S,=fdcpjd&j S r-sin ih <11 =

= зЬ//’(<-0 *<·

14)

В случае гармонически колеблющегося Д.

М=ql sin ~ I; (15)

излучаемая им за период Т энергия, на основании ур-ия (14),

S_T - Ί - (16)

где λ=νΤ—длина излучаемой Д. электромагнитной волны.

Лит.: Хвольсон О. Д., Курс физики, 2 изд., т. 5, стр. 339—405, Берлин, 1923; Эйхенвал ь д А. А., Теоретнч. физика, ч. 1—Теории поля, М.·—Л., 1027; Hertz II., Untersuchungen ii lier die Ausbrei-tung der elektr. Kraft. Lpz., 1914; Abraham M., Theorie der Elektrizitat. B. 1. 7 Aufl., Lpz., 1923; Cohn E., Das elektromagnetische Feld, 2 Auflage, Berlin, 1927. К. Теодорчин.

Диполь молекулярный. Всякая частица вещества всегда состоит из нек-рого числа разноименных электрическ. зарядов. Если в сумме эти заряды дают либо положительный либо отрицательный заряд, то имеется наэлектризованная частица, называемая и о и о м. Если же частица, например, молекула, электронейтральна, то центры масс всех положительных и всех отрицательных зарядов могут не совпадать. Если расстояние между этими центрами равно d (п л е ч о Д.), а сумма положительных зарядов (равная сумме отрицательных) равна е, то /i= ed

будет величиной электрич. дипольного момента. Дебай и Дж. Дне. Томсон предложили разделять молекулы на д и п о л ь н ы е, или полярные, обладающие б. или м. значительным готовим дипольным моментом, Ύ. е. Д. в отсутствии внешнего электрич. поля, и на неполярные (для них μ=0). К полярным относятся молекулы, построенные несимметрично из химически активных (а) и неактивных (b) групп по схеме [о—Ь]: ь ь

О

II

Ml

/Н N н н органич. вещества, содержащие углеводородную цепь или ядро, к одной стороне которых присоединены «полярные группы» —NH₂,—СО-ОН,—ОН,—N0₂ и др., например:

aba Ь

СООН — СН.СН.СН.СН,. η-валериановая к“та

Такие вещества имеют весьма высокую диэлектрическую постоянную (г), например:

^£h_so-⁸¹

^ьС_г11,ОП

= 22,

резко убывающую с температурой (Т): «молярная поляризация»

_п е — 1 М, b ^0_£t2D^_(,^r ’

где М—молекулярный вес, D—плотность, а а н b—постоянные, причем

(N

b=^4πΝ 9ft Т

число Авогадро, к=_N — постоянная Больцмана и μ—момент Д.); при этом а за висит от возможного смещения зарядов в молекуле под действием внешнего электрич. поля. Очевидно, что величину момента Д. можно определить из экспериментальных данных для изменения дпэлсктрпч. постоянной с Т. Т. о., получены значения:

/*NH,=1>53 -10 ^ls, ,“сн,он ⁼ 1>64 · ΙΟ¹», •^unci ⁼ 2,15 · 10-¹».

Порядок этих величин совпадает с вычисленными значениями: если принять заряд электрона е=4,77 · 10^-10 (в электростатических абсолютных единицах), а диаметр молекулы rfslO-»CAt, то,uas5 · 10-^ls. У неполярных веществ μ=ΰ или близко к 0. Их диэлектрнч. постоянная практически не изменяется с Т (Ь=0). В молекулах таких веществ или нот вовсе полярных групп (углеводороды) или полярные группы расположены симметрично и не образуют Д. Так, для окиси углерода/г_со =0,12· 10^_1“; для СН₃К0₂ (полярно) е=50. для симметричного же тетранптроме-тана CXNOj)· «=2,1, то есть имеет то же значение, что для всех неполярных углеводородов (s=2). Внешние электрич. поля, смещая заряды в молекуле («поляризуя» молекулу), увеличивают момент Д. или создают его, когда он ранее отсутствовал. В первом приближении Д. иногда можно считать жесткими, недеформнрующимися под действием внешнего поля.

Лит.: Debye Р., «Physik.ilische Ztschr.», Lpz., 1912, В. 13. р. 97; Jon а М., ibid., 1919, В. 20. р. 19; Handb. d. Radiologic, hrsg. v. Kr. .Marx, B. 0, p. 605—668, Lpz., 1925: Thomson J., «Philosoph. Mag.». L. 1914. 28, p. 757: Pauli V. «Ztschr. r. Physik», B., 1921, B. 6, p. 319. П. Ребиндер.