 > Техника, страница 43 > Дисперсия света
> Техника, страница 43 > Дисперсия света
Дисперсия света
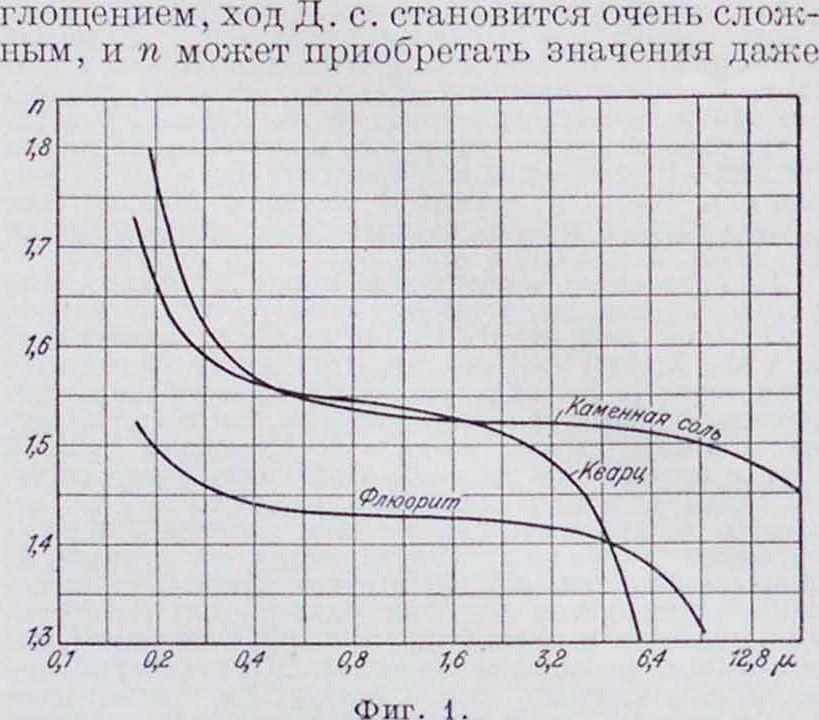
Дисперсия света, изменение скорости (фазовой) света в материальной среде в зависимости от частоты колебаний г, иными словами—изменение показателя преломления η в зависимости от длины волны Я. Для веществ, прозрачных в видимом спектре, п растет с уменьшением Я, чему и соответствует привычное радужное чередование цветов в спектрах, получаемых от прозрачных призм. Дисперсию света такого рода называ ют норм а л ь п о й. Па фигура 1 указан ход нормальной Д. с. для кварца, каменной соли и флюорита—веществ пшзрачных в очень широкой области спектра (Я на фигуре приведены в ,«). Однако, в тех областях спектра, где вещество обладает избирательным по-
меньшие 1 (относительно воздуха). Напр., для лучей Рентгена п меньше 1. На фигуре 2 изображена Д. с.—именно (и— 1)· 10°—для углекислоты при атмосферн. давлении (Я даны в μ). Фигура 2 захватывает очень большой спектральный интервал; при Я=4,31 /<, С02имеет сильную полосу поглощения, что и сопровождается резким изменением хода Д. с. (в центре самой полосы измерения произведены не были). Д. с. такого рода называется а н о м а л ь и о й.
Теория Д. с. основана на идее взаимодействия световых волн и элементарных резонаторов— атомов, молекул или элементов крнсталлич. решетки. В общем виде теория очень сложна; она упрощается, если предположить соответственно большинству практически важных случаев, что в объёме кубика с ребром, равным Я, содержится очень большое число молекул. В основу различных вариантов теории положены два дифференциальных ур-ия: ур-ие движения резонатора и ур-ис световой волны. Резонатор
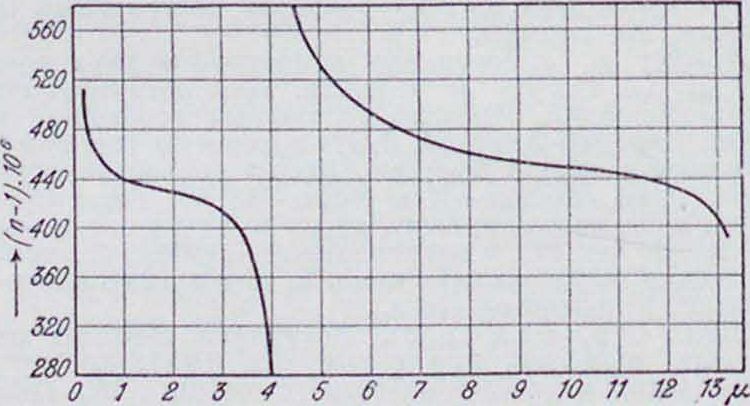
Фигура 2.
обыкновенно предполагается кпази-упругнм и обладающим затуханием, причем учитывается действие окружающей среды на резонатор; колеблющейся частью может быть электрон или целый заряженный атом. Под действием распространяющегося света молекулы приходят в вынужденные колебания, излучая при этом вторичные волны; фазы этих ноли, вообще говоря, отличаются от фазы падающей волны—они будут отставать или опережать последнюю в зависимости от соотношения v и частоты собственных колебаний молекулы г0. Изменение фазы определяет и изменение фазовой скорости. Два исходных ур-ия теории дают и два решения, относительно Д. с. и абсорбции, которые теоретически связаны неразрывно: если нет абсорбции, не м. б. и Д. с., которая в прозрачных частях спектра есть след наличия полос поглощения в других частях. Теория Ло-рентца приводит к следующим выражениям для п и для «индекса абсорбции»
I ί·+4* + f + гд +1’
2nV = /~(Ι + ΙΙ’ + Ί* _
сп у ( + V+n 1 ’
где у. 4 метров · т, о очN.e^Vo-vi)
Ί. “ Ч-ТП*-9·
(1)
(2)
(а)
при чем е—заряд и m—масса колеблющейся частицы, N—число резонаторов в единице объёма и д— коэфф. затухания, определяемый столкновениями молекул друг с другом, излучением или другими причинами. Величина * связана с экспериментально определяемыми величинами след, обр.: количество монохроматическ. света J, прошедшего через толщу поглощающего вещества г, выражается по закону Бугера уравнением: J=J0e~k!, где J0—количество света, входящего в вещество, к—экспериментально определяемая величина, связанная с * выражением: =
= 4л * ”, где с—скорость света. Формулы (1)
и (2) справедливы в том случае, когда имеются только резонаторы одного типа с частотою >0;если имеется несколько резонаторов с различными собственными частотами, то в правых частях уравнений (1) и (2) придется взять сумму, распространенную на все собственные частоты. Формулы (1) и (2) в раскрытом виде очень сложны, но они значительно упрощаются для многих практически важных случаев Д. с. Если поглощение невелико, то есть можно в первом приближении предположить, что д=0, и кроме того, пренебречь дробью */, (выражающей влияние окружающих молекул) в формуле для f, то у равнение (1), при переходе от частот к длинам волн, примет вид:
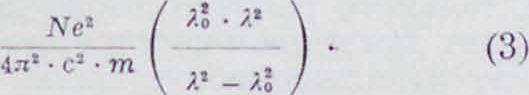
Эта формула (Селльмейера) охватывает как нормальную, так и аномальную Д. с., за исключением очень узкой области при λ=λ0, где она приводит к невозможным бесконечным значениям в соответствии с тем, что нами откинуто затухание. Если главная λ0 находится в далекой ультрафиолетовой части спектра, то для видимого спектра в первом приближении формулу (3) можно представить таким образом:
я» Λ+ *+£+·· (4)
Эта ф-ла, впервые предложенная Коши, довольно удовлетворительно охватывает область нормальной Д. с. обычных веществ и часто применяется для нрактич. целей градуировки спектральных приборов. Постоянные А, В, С,. могут быть найдены из уравнения (3), но для нрактич. целей находятся эмпирически по данным для п для нескольких λ. Формула (3) дана для случая резонаторов одного типа; в общем случае она принимает вид:
п-
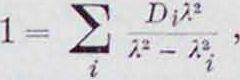
(5)
где индекс г соответствует различным частотам, a JJj—постоянные факторы, смысл которых ясен из ур-ия (3). Наир., Д. с. С02, представленная на фигуре 2, определяется четырьмя λ(, а именно: 720,41 А, 1 480,0 л, 4,31 μ и 14,91 μ. Если учесть откинутую х/3в выражении (а) для ΐ, по попрежнему пренебрегать (7, то уравнение (1) м. б. написано в таком виде:
п’ - i i 1
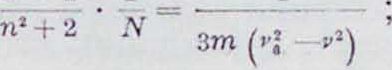
(6)
то есть для данной длины волны частное от на N есть величина постоянная, называемая рефракцией. Эта формула Лорент-ца-Лоренца имеет важное практич. значение для химич. анализа (смотрите Рефракция). Обыкновенно вместо N вводят пропорциональную числу резонаторов плотность (>, и выражение для рефракции получает вид:
Разность рефракций для 2 волн /.j
1
е
nj- i nj- i
V tiJ + 2 n!+ 2
= D
и λ2, т. e. (8)
иногда называют атомной (или соответственно молекулярной) Д. с. Уравнение (5) вполне отвечает опытным данным (пары одноатомных металлов, газы, растворы, кристаллы). По дисперсионным данным можно определять весьма точно собственные частоты и число поглощающих резонаторов. Теория квантов на основе принципа соответствия и волновой механики Шредингера приводит к выражению для Д. с., в пределах точности наблюдений совпадающему с уравнением (5). Разница состоит в том, что к «положительной» Д. с. (5) добавляется еще «отрицательная» Д. с., соответствующая возможности спонтанных переходов из верхних возбужденных энерге-тич. состояний атома в нижние. Если атом или молекула находятся в нормальном, невозбужденном состоянии, то отрицательная дисперсия света отпадает. Относительно практических методов измерения дисперсии света см. Рефрактометры.
Лит.:×и о ль сон О. Д., Курс физики, т. 5, глава 7—ст. Д. С. Рождественского "Электромагнитная теория света», Берлин. 1923; Falkenhagen II. Dispertion и. Absorption, Handbuch d. physikal. Optik, lirsg. v. E. Oehrcke, В. 1. p. 720, Leipzig, 1927; W о о d It. W. Researches in Physical Optics, N. V. 1921; Loren tz 11. A., The Theory of Electrons, Leipzig, 1916. С. Вавилов.