> Техника, страница 43 > Дифференциал

Дифференциал

Дифференциал, планетная передача, при помощи которой данный вал машины получает сумму или разность скоростей от двух разных источников движения.

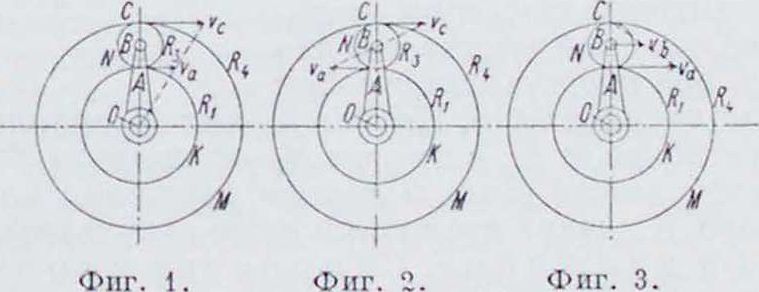
Схематически устройство Д. представлено на фигуре 1. Здесь на валу О вращаются вхолостую дне зубчатки К и M, могущие иметь каждая свое движение. Около той же геометрии. оси вращается рукоятка ОН, как кривошип, на пальце которого вращается планетная шестерня—с а т е л л и т—N, сцепленная одновременно с обоими колесами К и М;

рость колеса К при разных условиях. Для этого в остальной части механизма будем накладывать одно условие связи на ту или иную деталь. Обозначим радиусы колес: R!—для колеса К, —для рукоятки 013,

и._л—для сателлита У, R_t—для колеса М.

1-е д в и ж е н н е. Скорость р у к о я т-ки равна нулю. В этом случае (фигура 2) получим:

г.=- v_a или v,=R, со,=R₃ со, =

= —ν,=— R, ω,

откуда

u>=- _R ω, или η, =—£*·»«· (1)

Как видим, в этом случае сателлит, играет роль паразитного колеса, т. к. его радиус

и скорости не входят в формулу (1), то есть не влияют на передачу движения от колеса М к колесу К, но направление вращения при этом получается обратное.

2-е движение. Скорость колеса М равна нулю. Из фигура 3 видно, что в этом случае у сателлита точка С на мгновение будет неподвижной, то есть она является центром мгновенного вращения сателлита.

Отсюда непосредственно следует,что v_a =2 v,„ но V/,=R_? со», следовательно v_a= 21L ω₂=-= Ri-o>,

= 2 — · o)j или η”=2 -ρ* · n_a · (2)

,, откуда следует, что

ι Ra _____. _ Q R 2

“ R.

й.

Здесь опять сателлит оказывается паразитным колесом, причем скорости колеса К и рукоятки ОВ в этом случае отличаются друг от друга по величине, по направлению же совпадают.

Сумма движений. Одновременно вращаются: колесо М со скоростью и, и рукоятка со скоростью ω₂. Получаем теперь сложное движение, результат которого получается от сложения или вычитания составных скоростей, данных ф-лами (1) и (2). Т. о., результативная скорость колеса К в этом случае будет:. Н, R. 2R,a>_tTRt<°t

Ч₂ г. С0,=

2-ω.,

R.

й,

(3)

В этой формуле верхние знаки соответствуют тому случаю, когда колесо М и рукоятка имеют движение в одну и ту же сторону; при движении их в разные стороны нужно брать нижние знаки. Частный случай, разобран, выше Д., представлен на фигуре 4. Здесь на валу О, 0₂ свободно посажены колеса К и М, которые укреплены на втулках Е и F. На рукоятке L вращается сателлит в виде конич. шестерни. Т. о., в этом случае R,

— R_i=R_i. Теперь из формулы (3) получим:

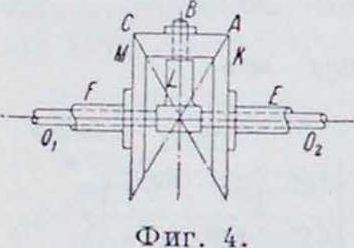
°>м=^шм ± ^ωΜ - ^2col ^{т ω}κ ^пМ ⁼ ~ⁿL “С ^п К

Правило знаков здесь остается то же, что и для ф-лы (3). Во всех рассмотренных выше случаях колесо М имело внутреннее зацепление с шестерней сателлита. На фигуре 5 представлен случай внешнего сцепления этих колес. Здесь рукоятка ОВ, колесо К и колесо М сохраняют прежнее значение. Что же касается планетной шестерни, то она здесь устроена иначе. Именно, в этом случае на пальце В вращаются сразу две са-теллнтовые шестерни, сидящие на одной втулке,так что они обе представляют собой одно твердое тело. Первая из них JV, сцеплена с колесом К, а вторая Л^г2—с колесом М. Разобранные выше 3 случая движения для этого Д. дадут несколько иные результаты.

1-е движение. Скорость рукоят-ки равна нулю. Мы получим обычное рядовое сцепление колес, и следовательно:

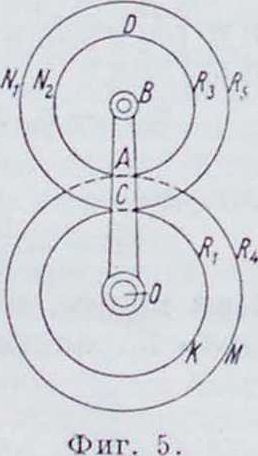
^ωί

К

R.R,

л, к,

^ωι

R,R_SК,К,

щ

(б)

При этом колеса К и ili будут вращаться в одну и ту же сторону, то есть знаки скоростей колес одинаковы.

2-е движение. Скорость колеса М равна ну л ю. В этом случае мгновенная скорость точки А сателлита равна нулю и является его центром мгновенного вращения. Таким образом,

По центру мгновенного вращения видно, что знаки V, и v_c противоположные. Обозначая длину ОВ через Jt₂ и угловую скорость рукоятки через ω₂, найдем v_b=R₂w₂, v_c== — Я,)», откуда

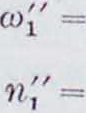
R,(R,-R,)

R,R,

ω₂

Ra (Re ^— R3) R,Ra

• n₂

(7)

Сумма д в и ж е н ий. Одновременно вращаются: колесо М со скоростью со₄ и рукоятка со скор остью т₂. В этом сложном движении результативная скорость колеса К будет равна:

СО,=COj ± со"

щ ---- п_х ± п

n,R_sa, R_a(R_s — Rj) ti), R,Ri

ΙΪ,ϋ,ΙΊ, : Rj(R_s- Rs)4j R,R.

(8)

Правило знаков для этой формулы такое же, как и для формулы (3).

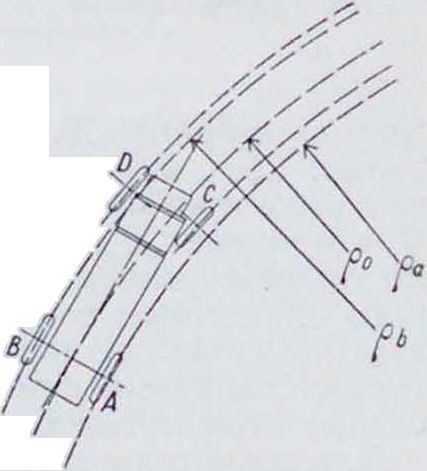
Д. автомобильный. При движении автомобиля по закруглению (фигура 6) ведущие колеса заднего моста А и В должны пробегать разные пути, которые пропорциональны радиусам кривизны п_а И Q_h их траекторий. Отсюда следует, что, во избежание скольжения одного из колес по грунту, заднюю ось нужно разрезать и предоставить колесам А и В возможность иметь независимые друг от друга движения. Если v₀ и <χ>„_Γ. в.

ω₀—линейная и угловая скорости движения ц. т. машины в дан-

оп + а,

ный момент времени, ρ₀=" —средний радиус кривизны, г — радиус заднего колеса, а—расстояние между колесами, со_а и со/,—углов, скорости вращения колес Пи В. ν_η и %—окружные скорости колес А и В, то:

откуда

Ч β ωο£/ι=rcob л Ч=<°oQa=γωα 1	Ο)
<uh __ Qh ωα Qa	(Ю)

Как видно, отношение скоростей двух задних колес при движении по закруглению не зависит от средней скорости машины, а определяется радиусами кривизны траекторий. Определим разности в скоростях каждого колеса но сравнению со средней скоростью машины:

Ч - г>₀=гсо_ь - ρ₀ω₀ i ^να - v₀=Г(О_а - ρ₀ω₀ I

(Π)

Решал совместно ур-ия (9) и (11), получим: V_b - V₀=ω₀ (»_ft - n₀)=ω„ “

«α - го ^ "о (Sa -во) - °>о “

Из уравнений (12) легко получить

(12)

«I, га,

(13)

(15)

Ф-ла (13) показывает, что разность угловых скоростей колес А и В прямо пропорциональна расстоянию между колесами, средней линейной скорости машины и обратно пропорциональна радиусу колеса и среднему радиусу закругления. Если машина идет по прямолинейному пути, то ω₀=0, и из уравнения (13) найдем, что ω,=ω_α. Если одно колесо, например А, остановить, то г„=0,и из уравнения (12) получим ν₀=ω₀", откуда

v_h~a>₀-a. (14)

Наконец, если повертывать машину при н₀=0, то

^vb~ ^ω0 2 I

^va=- ^ω0 2 )

Соотношения (14) и (15) соответствуют очень крутым поворотам и практически невозможны, т. к. передние колеса по своей конструкции не приспособлены для этого. Что же касается задних колес, то все отмеченные выше функции они могут выполнять при помощи Д. С этой целью задняя ось разрезается на две части, чтобы предоставить возможность колесам А и В иметь разные скорости, затем разрезанные части этой оси соединяются между собой при помощи Д.

Схема Д. показана на фигуре 7. Здесь О_г и 0₂две части задней оси, на каждой из к-рых укреплено по кони-ческ. зубчатке К и М. Шестерня В заклинена наглавном валу машины А и сцеплена с коронной зубчаткой D. В этой последней в ободе имеются специальные втулки, в которых вращаются планетные шестерни С, С (две, три или четыре). Планетные шестерни сцеплены сразу с обоими колесами К и М. Движение от машины через ват А передается коронному колесу D и отсюда через шестерни С, С обоим колесам с одинаковой скоростью. Если теперь вал машины затормозить и повернуть одно колесо, например М, но часовой стрелке, то нетрудно убедиться в том, что при этом колесо К повернется в противоположную сторону, причем скаляры угловых скоростей будут для обоих колес равны друг другу, в соответствии с формулой (15). Если

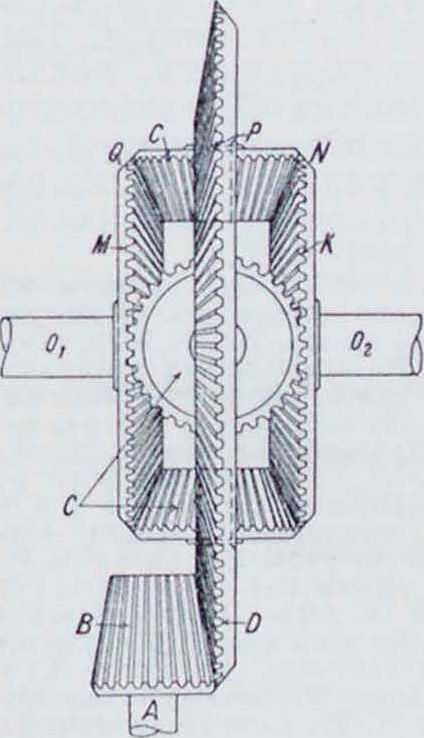
Фигура 7.

затормозить колесо М, то скорость точки Q на начальной окружности зубчатки будет равна нулю, а скорости центра планетной шестерни Р и точки N на начальной окружности другой зубчатки будут пропорциональны расстояниям этих точек от точки Q, являющейся в этом случае центром мгновенного вращения планетной шестерни, то есть г>_п=2г>_;,. Это находится в полном соответствии с ф-лой (14). Из конструкции Д. видно, что если угловая скорость одного колеса, например ili, окажется больше угловой скорости коронного колеса на нек-рую величину, то ровно на такую же величину скорость колеса К окажется меньше скорости коронной зубчатки. Это соответствует ф-лам (12). Конструктивно автомобильные Д. выполняются различно. Наиболее распространенной является система, соответствующая схеме, представленной на фигуре 7. Б про-д о л ь н ы х Д. на валу машины (например, сист. Mercedes) укреплены поперечные пальцы, на которых вращаются конические сателлиты. От этих последних через втулки движение передается непосредственно зубчаткам, которые укреплены на концах полуосей. Такие Д. применяются в машинах Mercedes, La Buire, грузовиках Renault и др.

Д. банкаброшный. Основные детали банкаброша (фигура 8) состоят из вытяжных цилиндров а, а, веретена с рогулькой β и катушки у, на которую наматывается пряжа

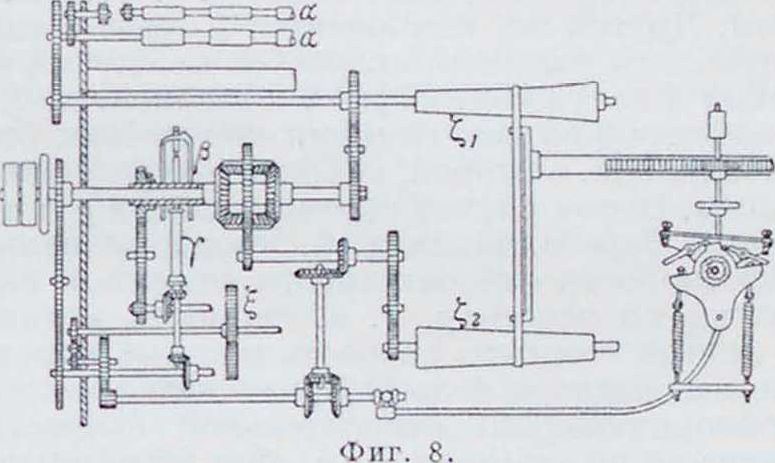
(ровница). Т. к. цилиндрами а в единицу времени подается одно и то же количество ровницы, а по мере наматывания ее на катушку диам. початка возрастает, то, очевидно, скорость вращения катушки нужно изменять. При этом одновременно выполняется другая операция—крутка ровницы веретеном. Крутка эта должен быть постоянной. Т. о., получается задача: дать постоянное число оборотов веретену и переменное но известному закону— катушке. Катушка поэтому выполняет два движения: вместе с веретеном она участвует в процессе крутки и получает число оборотов веретена и, кроме того, имеет дополнительные обороты, положит, либо отрицательные, для намотки ровницы, причем скорость этого дополнительного движения должна меняться номере нарастания початка и увеличения диам. мотки. Сложное движение катушки осуществляется в банкаброшах при помощи Д. Вся установка Д. здесь существенно отличается от автомобильной тем, что там колеса сами используют предоставленную им лишнюю степень свободы, а у банкаброшей оба движения Д. выполняются по наперед заданным кинематическ. условиям.

Одно движение синхронно с движением веретена, следовательно, идет с постоянной заданной скоростью. Другое регулируется коническими барабанчиками £, и ζ₂, от которых через Д. вращение передается катушкам. От этих лее конич. барабанчиков движение идет еще, помимо Д., к каретке, поднимающей и опускающей при помощи реек ξ катушки в процессе мотки. Скорость этого подъема изменяется по мере нарастания диаметра початка. Именно, пусть щ—полное число оборотов катушки, а щ—веретена, <5—толщина одного витка пряжи, D—диам. мотки (толщина початка, взятая по средним линиям витка), L—длина ровницы, выпускаемой в единицу времени, ν—скорость движения каретки; тогда

L=лВ{п_к — щ), (16)

υ=(п_к - n_b)S=^lf_D · (17)

При переводе ремня на конич. барабанчиках одновременно изменяются скорости катушки (через Д.) и скорость подъема каретки (помимо Д.). Установим закономерности в этих изменениях. Данные выше ф-лы (3) и (8) показывают, в применении к банкаброшам, что число оборотов катушки молено составить из двух компонентов на Д. п( и л/, причем один из них, например ni, можно подобрать так, что он будет передавать катушке ровно столько оборотов, сколько имеет веретено, и ото число м. б. постоянным. Другой лее компонент п", будет тогда управлять разницей скоростей между веретеном и катушкой. Первый компонент должен быть, следовательно, вне влияния конических барабанчиков, а второй, наоборот, под их влиянием. В этом случае перемена скоростей на конич. барабанчиках должен быть пропорциональной скорости относительного движения катушки по веретену, то есть скорости мотки. С другой стороны, скорость подъема каретки, как видно из ф-лы (17), изменится так же пропорционально относительной скорости катушки по веретену. Т. о., при перестановке ремня на конических барабанчиках механизм будет работать правильно. Ив той лее ф-лы (17) мы видим основания для проектирования конич. барабанчиков, так как зависимость между диам. наматывания и скоростью поступательного движения каретки здесь определяется в форме vD=Const, т. с. равнобочной гиперболы.

Конструктивно банкаброшные Д. отличаются от автомобильных тем, что для упра-

Фнг. 9.

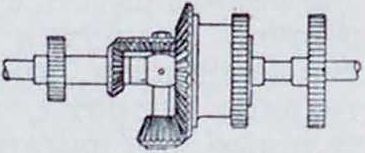
Фигура 10.

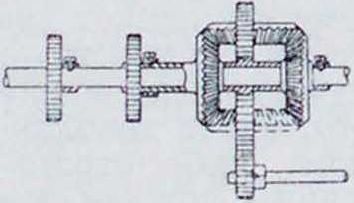
вления каждой частью движения в них имеются приводные шестерни. Их должен быть 3: одна коронная и две сцепленные с зубчатками Д. Другая особенность заключается в том, что оба колеса Д. К и М (смотрите выше) здесь могут вращаться и в одном и в нротивополож-ных направлениях, чего нельзя сделать у автомобиля, т. к. у банкаброша от Д. до ка тушки имеется целый зубчатый перебор, с помощью которого направление вращения легко изменяется. Наконец, вал Д. здесь молено но разрезать, а выполнить его в виде двойного: одного сплошного, а другого трубчатого. На фигуре 9—12 показаны разрезы

Фигура 11. фигура 12.

нек-рых ходовых конструкций: Goodsworth (9), Tweedelo (10) с конич. сателлитами; Curtis & Rhodes (11) и Brooks & Doxey (12)— с цилиндрическими. Особую конструкцию представляет Howard & Bullough (13).Здесь на косо срезанной широкой цнлиндрич. трубе А—А скользит дисковый бурт двойной конич. зубчатки В—В, сцепляющейся одновременно с колесами К и М. При повороте коронной шестерни С труба А поворачивается, вместе с тем двойная зубчатка В, повертываясь на шаровой поверхности 2), катится по зубчаткам К и М.

Д.-регулятор. Нз общей теории Д. вытекает возможность еще одного важного использования его. Фигура -1 показывает, что если колеса К и М вращаются в разные стороны с одинаковой скоростью, то рукоятка будет неподвижна. Напротив, она приходит в движение, как только скорости этих колес оказываются неодинаковыми. В этом виде механизм употребляется у морских судовых двухвинтовых машин для обеспечения равного числа оборотов обоих винтов. Как только это равенство нарушается, приходит в движение рукоятка Д., кинематически действующая на паровпускные органы обеих машин, и регулирует, т. о., их работу. Существует много конструкций и областей применения дифференциала.

Лит.: 1¹J М а л и ш е в А., Анализ и синтез механизмов с точки зрения их структуры, «Известия Томского технологического ин-та», Томск, 1923, т. 44, иын. 2; М а л ы ш в Λ. II. Прикладная механика, ч. 1. вып. 2— Структура и синтез механизма. Новони-колаевск, 1923.

Таггарт В. С., Прядение хлопка, т. 2. М., 1923; Кир и и ч е в В. Л., Конспект лекций по прикладной механике, СПБ, 1910 (литогр.);×а и-т о и В. А., Механика текстильных машин, пер. с англ., Иваново-Вознесенск. 1927; В и г к а г <1 I“. Discussion du nmuveinont different iel. «L*industrie textile», Paris, 1889; Pag 6 V“, The Modern Gasoline Automobile. N .Y. 1924; В о и a s s e H., Theories des vecteurs, Cin6matique, MOcanismes, P., 1921; II i s-c о x G., Mechanical Appliances. Mechanical Movements,

5 ed. I,.1929; В г о w н II. T. Bewegungsmcchanis-mci). aus d. Kngl. Obers. Lpz., 1925. А. Малышев.